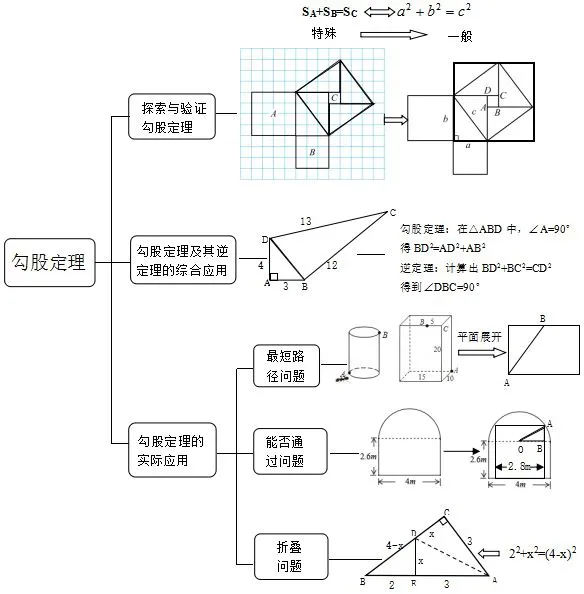
依托思维导图 构建高效课堂—以“勾股定理”复习课教学为例

广东省佛山市华英学校(528000) 黎春玉

广东省佛山市第一中学(528000) 吴统胜

思维导图作为一种行之有效的思维工具,不仅对学生平时学习新知识很有帮助,在学生的数学复习中更是占据着无可替代的位置,发挥着不可估量的作用.思维导图更可以作为一种高效的学习模式被应用到复习过程当中,它不仅能改善学生的认知方式,提升数学复习效果,还能提高学生整合知识的能力,对学生进行建构性学习有很大的促进作用,是培养学生数学解题能力和思维能力的有效手段.

通过建构“勾股定理的思维导图”对这一章进行知识的“回顾与思考”,梳理知识结构,形成知识系统,不仅可以培养学生回顾与反思的习惯,更能促进学生获得知识系统的自主建构能力.当然,知识系统的建构并不是“空对空”的回忆,还需要借助典型问题,对有关重点知识进行巩固运用.借助思维导图可以把知识系统的建构与典型例析有机结合起来,达到关注知识的发生发展过程,关注学生运用知识解决问题的水平,关注学生在解决问题方法的多样性、解决问题之后的回顾与反思、变式拓展等目标.

本节复习课的设计思路是首先建构“勾股定理”思维导图,然后依托思维导图,构建高效的复习课堂.

首先让学生翻看北师大版八年级上册教材重现勾股定理这一章的知识发生发展的过程,由于勾股定理这一章知识点较少,知识梳理相对简单,在教师的引导下学生能完成本章知识系统的初步建构：

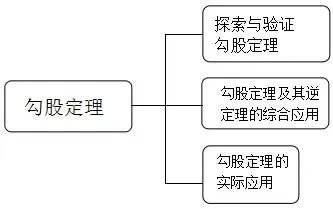
下面在引导学生回顾本章知识的基础上,对学生初步建构的知识系统架构进行添砖加瓦,逐步完善本章思维导图的建构,展开高效复习课堂：

一、回顾探索与验证勾股定理的过程,揭示勾股定理的探索与验证活动过程所蕴含的丰富的数学思想,如数形结合、化归思想等,由代数表示联想到有关几何图形,由有关几何图形联想到代数表示,从而渗透数形结合思想,认识数学知识的内在联系.

(一)呈现勾股定理探索与验证的知识发生发展过程,渗透由特殊到一般的化归思想以及数形结合思想.

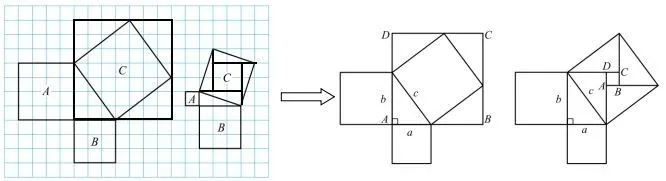
图1

SA+SB=SC⇔a2+b2=c2

典型例析目的是考察学生对勾股定理的验证过程的掌握情况,关注学生的过程性学习.

如图2,有四个全等的直角三角形,它们的两直角边分别为a、b,斜边为c,以及一个边长为c的正方形,请用所给的图形拼成一个可以证明勾股定理的图案．

(1)画出你拼成的图形.

(2)用你所画图形证明勾股定理.

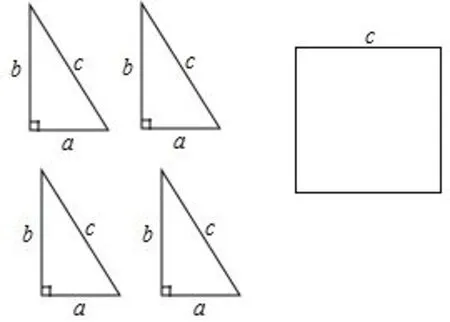
图2

(二)引导学生思考勾股定理与完全平方公式这两者验证过程之间的联系.增强学生对新旧知识间关联的反思和总结能力,渗透数形结合的数学思想.

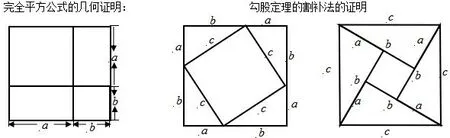
图3

共性(1)都是利用a2几何的意义是边长为a的正方形的面积进行构图；

(2)都对所构的图形进行割补；

(3)利用同一个图形的不同面积计算方法解决恒等式的证明.

典型例题(课本第17页第7题)据传当年毕达哥拉斯,借助如图4所示的两个图形,验证了勾股定理,你能说说其中的道理吗?

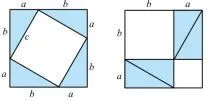
图4

(三)勾股定理验证过程的知识拓展一：引导学生归纳总结出勾股定理证明过程中格点正方形的面积的多种计算方法,关注学生解决问题的方法多样性.

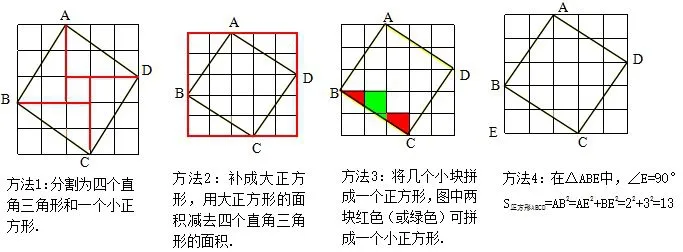
图5

(四)勾股定理验证过程的知识拓展二：知识的进一步拓展由格点正方形的面积计算拓展到一般的格点多边形的面积计算,继续渗透特殊到一般的数学化归思想.

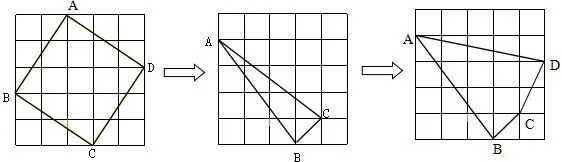
图6

(1)在图6-2中对于格点△ABC你能提出哪些问题?

问题1：上述的哪些计算方法能迁移到计算格点△ABC的面积?

问题2：你能判断格点△ABC是不是直角三角形?(勾股定理及其逆定理的应用)

问题3：你还能解决什么问题?(比如格点△ABC的AB、AC边上的高)

(2)求图6-3中格点四边形的面积.

(五)勾股定理验证过程的知识拓展三：勾股定理的逆向应用,进一步培养学生的逆向思维.

典型例题(课本第17页第9题)如图7,方格纸上每个小正方形的面积为1个单位.

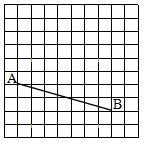
图7

(1)在方格纸上,以线段AB为边画正方形并计算所画正方形的面积,解释你的计算方法；

(2)你能在图上画出面积依次为5个单位、10个单位、13个单位的正方形吗?

二、引导学生翻看教材,对勾股定理及其逆定理的综合应用进行举例及变式.引导学生回归课本,加强对数学知识的整合能力.

例1在四边形ABCD中,∠A=90°,AB=3,BC=12,CD=13,DA=4,求四边形ABCD的面积.(课本第9页例题变式)

例2在正方形ABCD中,AB=4,AE=2,DF=1,DA=4,图9中有几个直角三角形?你是如何判断?(课本第10页随堂练习2)

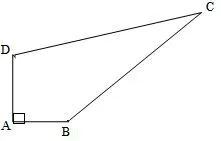
图8

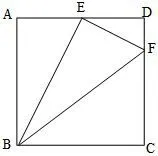
图9

三、引导学生翻看教材,举例说明勾股定理的实际应用,并对典型例题进行分类整合.

(一)应用一 解决不在同一平面内两点间最短路径问题.渗透数学的化归思想：把不在同一平面内两点间最短路径问题通过平面展开图化归为同一平面内“两点之间,线段最短”问题.关注学生解决问题之后的回顾与反思.

典型例析(课本第13页引例)如图10所示,有一个圆柱,它的高等于12cm,底面上的圆的周长等于18cm,在圆柱下底面的点A有一只蚂蚁,它想吃到上底面上与点A相对的点B处的食物,沿圆柱侧面爬行的最短路程是多少?

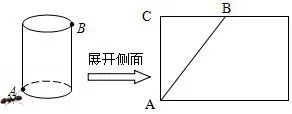
图10

解将圆柱体的侧面展开,连接A、B,根据两点之间线段最短,根据题意可得：AC=12cm,BC=9cm 在△ABC中,∠C=90°,所以AB2=AC2+BC2=122+92=225=152,所以AB=15cm,所以沿圆柱侧面爬行的最短路程是15cm.所以它需爬行的最短路程约是15cm.

典型例析(课本第19页第12题)如图11,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离为5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是多少?

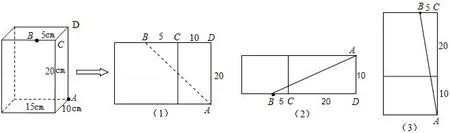
图11

分析由于长方体表面展开的方式很多,不同的展开方式下最短路径有所不同,因此学生在课堂训练有可能在分类讨论时出现错漏,所以课堂上教师有必要给予一定的指导和示范,以达到扫除盲点的目的.

解将长方体表面展开,连接A、B,根据两点之间线段最短,

(1)如图,BD=10+5=15,AD=20,由勾股定理得：AB2=AD2+BD2=152+202=625=252.

(2)如图,BD=20+5=25,AD=10,由勾股定理得,AB2=AD2+BD2=102+252=725.

(3)如图,BC=5,AC=20+10=30,由勾股定理得：AB2=BC2+AC2=52+302=925.

因为625＜725＜925,所以需要爬行的最短距离是25cm.

(二)应用二 能否通过问题.关注学生运用知识解决问题的能力水平.

典型例析(课本第197页第27题)一辆卡车装满货物后,高4米,宽2.8米,这辆卡车能通过横截面如图12所示(上方是一个半圆)的隧道吗?

分析此题无论是理解题意、应用知识解决问题还是解题的规范表达对学生来说存在一定的困难,课堂上教师应重点引导学生画出图形,借助图形进行分析,最终化归为勾股定理的应用,并示范解题过程.解如图,由题意得,在 Rt△OAB中,AB2=OA2-OB2=22-1.42=2.04,因为2.04＞1.96,所以AB＞1.4,所以此时隧道能通过的最大高度：AH=AB+BH＞2.6+1.4=4(米),所以这辆卡车能通过此隧道.

磷肥是作物必需的第二大营养元素肥料，对促进作物生长和保障粮食安全有着非常重要的作用。据中国工程院院士、中国农业大学教授张福锁介绍，上个世纪80年代，我国土壤中的含磷量非常低，全国大约有80%的土壤缺磷，合理搭配施用磷肥对作物增产的效果非常明显。“自从有了磷肥，我国的粮食产量才开始大幅增长。可以说，如果没有磷肥和磷肥工业的支撑，中国的粮食安全就无法得到保障。”张福锁表示，“多年来，中国磷复肥大国地位持续巩固，在技术、装备、产品、服务创新等方面不断实现超越。”

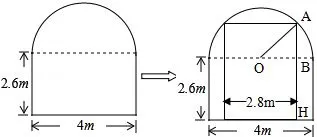
图12

(三)应用三 勾股定理应用中所涉及的建模思想、方程思想.渗透数学建模思想.关注学生在解决问题之后的回顾与反思、变式拓展.

1.典型题目(课本P15第5题)在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：有一个水池,水面是一个边长为10尺的正方形,在水池正中央长有一根芦苇,芦苇露出水面1尺.如果把这根芦苇拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池深和这根芦苇各是多少尺?

图13

2.典型例析如图14,有一个直角三角形纸片ABC,两直角边AC=3,BC=4,现将直角边AC沿线段AD折叠,使它落在斜边AB上,且与AE重合,则CD的长是多少?

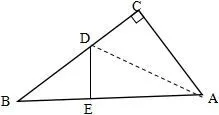
图14

分析由于学生初步接触几何中的折叠问题,所以不宜作为课堂学习的起始问题,但可以作为复习课中的知识拓展,目的是通过本题的分析和解答过程,培养学生标注图形信息的习惯.引导如下：

(1)图中哪些线段是已知的?哪些线段易求得?请在图中标注出来.

(2)若设CD为x,图中哪些线段能用x表示,请在图中标注出来.

(3)用哪些知识能建立x的方程?

解因为两直角边AC=3,BC=4,根据勾股定理得,AB=5,由折叠得,DE=CD,AC=AE=3,∠DEB=90°,设CD=xcm,则BD=(12-x)cm,在 Rt△BDE中,DE2+BE2=BD2,即x2+(5-3)2=(4-x)2,解得：x=1.5,所以CD的长是1.5.

变式1如图15,有一个直角三角形纸片,两直角边AC=3,BC=4,现将直角边BC沿线段BD折叠,使它落在斜边AB上,且与BE重合,则CD的长是多少?

变式2如图16,已知长方形ABCD中AB=4,BC=5,在边CD上取一点E,将△ADE折叠使点D恰好落在BC边上的点F,则CE的长是多少?

图15

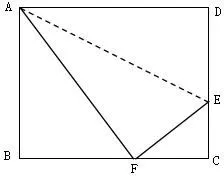
图16

本节课对勾股定理这一章进行复习,依托思维导图来回忆勾股定理所有的知识点及相关的知识.先构建一个总体的框架,再逐条进行挖掘和深化,把要复习的内容直观地呈现在学生面前,引导学生对相关知识结构进行梳理,激发学生对所学知识的记忆,使学生在回顾知识的同时,构建一个清晰的知识结构框架.使学生在此过程中形成对勾股定理这一章知识总体的把握和直观的认识,从而在实际的解题中,可以更加快速、轻松地找到解题方法.

通过课堂教学,引导学生对勾股定理这一章的知识进行回顾、思考、分类、重组,并借助典型的例析作为知识的载体,渗透数形结合思想、化归思想、建模思想、方程思想等数学思想,提升学生数学思维品质,促进学生最终建构和生成如右侧的勾股定理思维导图.

在初中数学复习中应用思维导图,不仅能在复习课上启迪学生的思维再现,让学生在思维再现的过程中温故而知新,还能让学生的知识与技能的储备得到系统性的建构和完善.学生在复习过程中不仅注重解题方法和技巧的积累,更注重方法与经验的总结,不仅解决了学生原先存在的思维困惑和误区,还提升了学生的思维站位高度,并能在一定程度上减轻教师的教学负担,活跃课堂气氛,极大地提高了数学课堂的复习效果.

常言道：“授人以鱼,不如授人以渔.”著名教育家叶圣陶先生也曾说过：“我以为好的先生不是教书,不是教学生,乃是教学生学.”依托思维导图,通过教师的精心备课和巧妙设计,构建高效课堂,较大限度地激发学生的学习热情,使学生的学习过程成为在教师引导下的“再创造”过程,不仅达成了“授之以渔”的良好教学效果,还能达到师生之间共“渔”的效果,让学生在不知不觉中完成了知识的建构、方法的达成、思想的渗透,真正夯实学生基础,并使知识系统化、网络化,还能深化学生对数学知识和方法的认识和理解,真正领悟到数学的思想和知识的结构,促进其创造性思维能力的发展,充分调动和发挥出学生的内在潜能,是教学中的“润物细无声”.