2018年北京高考数学理科压轴题剖析
2019-04-09汪燕铭卢发接
汪燕铭 卢发接
(北京师范大学第二附属中学 100088)
2018年北京高考数学卷的试题继承了“大气、平和,贯通融合”的特点,在试题的呈现方式,题材的选取,能力立意和数学核心素养的考查等方面都进行了很好的探索[1].试卷结构稳定,难易程度适当,注重数学素养和创新能力的考查,试题内容立足主干知识,密切联系学生的学习和生活实际,充分体现数学在应用、文化和教育方面的价值,达到了《2018年普通高等学校招生全国统一考试北京卷考试说明》[2]中要求突出数学试题的能力立意,强化对素质教育的正确导向的目的.
北京高考数学卷理科压轴题特色鲜明,一直受到社会各界的广泛关注.该题通常没有固定的解题套路,在平时训练中很少见到类似的题型,需要学生阅读题目内容,理解题中定义的新概念或新运算的含义,探究它们的性质,并应用于解决问题.2018年北京高考数学理科压轴题以集合为载体,定义了一种新运算,通过基本计算和求满足给定条件的集合元素个数的最大值,重点考查学生的抽象概括能力和推理论证能力.
题目设n为正整数,集合A={α|α=(t1,t2,…,tn),tk∈{0,1},k=1,2,…,n}.对于集合A中的任意元素α=(x1,x2,…,xn)和β=(y1,y2,…,yn),记
(Ⅰ) 当n=3时,若α=(1,1,0),β=(0,1,1),求M(α,α)和M(α,β)的值;
(Ⅱ) 当n=4时,设B是A的子集,且满足:对于B中的任意元素α,β,当α,β相同时,M(α,β)是奇数;当α,β不同时,M(α,β)是偶数. 求集合B中元素个数的最大值;
(Ⅲ) 给定不小于2的n,设B是A的子集,且满足:对于B中的任意两个不同的元素α,β,M(α,β)=0.写出一个集合B,使其元素个数最多,并说明理由.
在本文,我们首先给出新运算M(α,β)的一个等价定义,然后基于此定义给出上述压轴题的另一种解法.最后,我们分析该问题的高等数学背景,进一步认清运算M(α,β)的本质,同时给出第3问的更简洁的解法.
1 压轴题中M(α,β)的等价定义与压轴题的另解
注意到,对任意x,y∈R,
我们发现,当x,y=0或1时,总有min{x,y}=xy.
于是,对任意α=(x1,x2,…,xn),β=(y1,y2,…,yn)∈A,
M(α,β)=x1y1+x2y2+…+xnyn.
(1)
这样一来,经过推理论证和抽象概括,我们得到了M(α,β)的一个等价定义,其表达式更加简洁优美和熟悉.基于此定义,我们可以给出该压轴题的另一种解法.
解(Ⅰ) 由(1)式直接计算得:M(α,α)=2,M(α,β)=1.
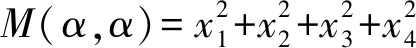
α1=(1,0,0,0),α2=(0,1,0,0),α3=(0,0,1,0),α4=(0,0,0,1),
β1=(1,0,1,1),β2=(1,1,0,1),β3=(1,1,1,0),β4=(0,1,1,1).
而M(αi,βi)=1,故αi与βi不能同属于B,i=1,2,3,4.由此推出,B中至多4个元素.而B={α1,α2,α3,α4}满足条件,故B中元素个数的最大值为4.
(Ⅲ)先用数学归纳法证明:当n≥2时,|B|≤n+1.
当n=2时,A中有4个元素α1=(0,0),α2=(1,0),α3=(0,1),α4=(1,1).由于M(α2,α4)=1,M(α3,α4)=1,故当α4∈B时,α2,α3∉B,此时|B|≤2;当α4∉B时,|B|≤3.结论成立.
假设n=k时结论成立.那么,当n=k+1时,对任意α=(x1,x2,…,xk+1)∈A,记
α′=(x1,x2,…,xk).
如果B中每个元素的第k+1个分量为0,令B′={α′|α∈B},则|B|=|B′|,且对任意α′,β′∈B′,M(α′,β′)=M(α,β)=0.由归纳假设知,|B′|≤k+1,从而|B|≤k+1.如果B中存在一个元素α=(x1,…,xk,1),则对任意β=(y1,y2,…,yk+1)∈B,β≠α,由于M(α,β)=0,故0=x1y1+…+xkyk+yk+1≥yk+1≥0,从而yk+1=0.令B′={β′|β∈B,β≠α},则|B|=|B′|+1.由归纳假设知,|B|≤(k+1)+1=k+2.结论仍然成立.
因此,当n≥2时,|B|≤n+1.
再选取B={α1,α2,…,αn,αn+1},其中
(2)
则|B|=n+1,且对任意α,β∈B,β≠α,都有M(α,β)=0.
综上所述,B中元素个数的最大值为n+1.
需要指出的是,(Ⅱ)和(Ⅲ)的证明过程都需要学生具有一定的推理论证的能力.例如,要证明集合B中元素个数的最大值为某个确定的数a,首先要证明对满足条件的每个集合B,其元素个数不超过a,然后证明存在一个满足条件的集合B,其元素个数恰好为a.另外,(Ⅲ)的证明过程还要求学生具有抽象概括的能力.例如,要得到集合B中元素个数不超过n+1,先要考察一些特殊情形,如n=2,3,4的情形,发现集合B中元素个数分别不超过3,4,5,由此抽象出一般规律,然后用数学归纳法严格证明.
2 压轴题的高等数学背景
从(1)式可以看出,运算M(α,β)与欧氏空间Rn中的内积之间有密切的关系.首先,我们回顾欧氏空间的概念.
定义[3]设V是实数域R上一个向量空间.若对V中任意一对向量α,β,都有一个确定的记作(α,β)的实数与它们对应,并且满足下列条件:
①(α,β)=(β,α);
②(kα,β)=k(α,β);
③(α+β,γ)=(α,γ)+(β,γ);
④当α≠0时,(α,α)>0,
这里α,β,γ是V中的任意向量,k是任意实数,则称(α,β)为α与β的内积,定义了内积的R上的向量空间V称为欧氏空间.
在欧氏空间V中,如果向量α,β满足(α,β)=0,则称α与β正交.
命题[3]设V为欧氏空间,α1,α2,…,αm∈V为两两正交的非零向量,则α1,α2,…,αm线性无关.
我们知道,Rn是R上的n维向量空间.对任意ξ=(x1,x2,…,xn),η=(y1,y2,…,yn)∈Rn,规定:
(ξ,η)=x1y1+x2y2+…+xnyn.
容易验证,(·,·)满足条件①~④.因此,它是向量空间Rn的一个内积,从而Rn关于这个内积作成一个欧氏空间.
注意到,压轴题中的集合A是Rn的非空子集.再由(1)式知,定义在A上的新运算M(α,β)本质上就是α与β的内积.利用欧氏空间的基本知识,我们很容易给出压轴题第3问的一个简洁证明.
(Ⅲ)的证明由命题知,Rn中彼此正交的非零向量一定是线性无关的,而集合B是由A中若干个彼此正交的向量构成的集合,故B中非零向量的个数不超过Rn的维数n.由于零向量与任何向量正交,故B中向量的个数不超过n+1.另一方面,A中存在n+1个彼此正交的向量,如(2)式中给出的α1,α2,…,αn+1.因此,B中元素个数的最大值为n+1.
我们发现,本文讨论的题目与2010年北京高考数学理科压轴题有相似的数学背景.后者叙述如下:
已知集合Sn={X|X=(x1,x2,…,xn),xi∈{0,1},i=1,2,…,n}(n≥2)对于A=(a1,a2,…,an),B=(b1,b2,…,bn)∈Sn,定义A与B的差为:
A-B=(|a1-b1|,|a2-b2|,…,|an-bn|);
A与B之间的距离为:
(3)
(Ⅰ) 证明:∀A,B,C∈Sn,有A-B∈Sn且d(A-C,B-C)=d(A,B);
(Ⅱ) 证明:∀A,B,C∈Sn,d(A,B),d(A,C),d(B,C)三个数中至少有一个是偶数;
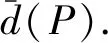
这两题都是以共同的集合为载体,在集合上定义新运算,先让学生探究新运算的一些基本性质,然后证明有关新运算的不等式.尽管本文讨论的压轴题第3问是求最大值,但本质上也是证明一个关于运算M(α,β)的不等式.另外,前者的高等数学背景是欧氏空间Rn(定义了内积的R上的向量空间),运算M(α,β)为向量α与β的内积;后者的高等数学背景是赋范向量空间Rn(定义了范数的向量空间)[4],其中范数为
||x||1=|x1|+|x2|+…+|xn|,
∀x=(x1,x2,…,xn)∈Rn.
由(3)式知,运算d(A,B)实际上为范数||·||1导出的向量A与B之间的距离,即
d(A,B)=||A-B||1,
这里,A-B为向量空间Rn中向量A与B的差.作为中学数学教师,我们需要透过题目表面,挖掘其背后的数学本质.这样做的目的,并不是要给学生讲解这些题目背后的高等数学背景,而是让自己的解题教学尽可能地做到有章可循.
