数学问题解答

2019年1月号问题解答

(解答由问题提供人给出)

(湖北省谷城县第三中学 贺斌 龚为民 441700)

(1)

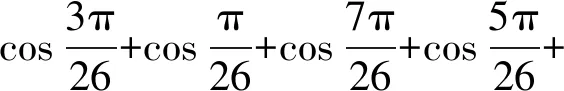
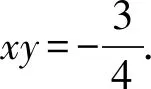
(2)

因为

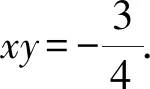
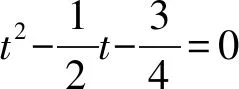
2462已知 如图，AB为⊙O的直径，弦CD⊥AB于点E.点M1、M2在OC上，且CM1=OM2.直线AM1、AM2分别交⊙O于点N1、N2.求证：

S△DCN1·S△DCN2=S△DBN1·S△DBN2.

(北京市芳草地国际学校富力分校 郭文征 郭璋 100121)

证明如图，连接AC，设AN1、AN2分别与BC交于点F1、F2，△ACN1边AN1上的高为h1，△ABN1边AN1上的高为h2(即BN1).

(Ⅰ)

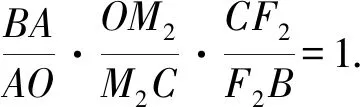
(Ⅱ)

因为CM1=OM2，

所以CM2=OM1.

又AB为⊙O的直径，AO为⊙O的半径.

(Ⅲ)

因为A、C、N1、B四点共圆，

所以∠ACN1+∠ABN1=180°.

所以sin ∠ACN1=sin ∠ABN1.

(Ⅳ)

同理可证

(Ⅴ)

由(Ⅳ)×(Ⅴ)得

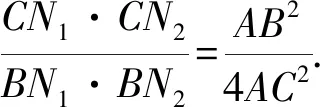
(Ⅵ)

易证Rt△ABC∽Rt△DBE.

(Ⅶ)

由(Ⅵ)和(Ⅶ)得

所以(DC·CN1)(DC·CN2)

=(DB·BN1)(DB·BN2).

因为C、D、B、N1四点共圆，

所以sin ∠DCN1=sin ∠DBN1.

同理可证sin ∠DCN2=sin ∠DBN2.

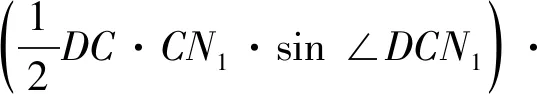
所以S△DCN1·S△DCN2=S△DBN1·S△DBN2.

2463设a,b,c>0,求证：

(陕西省咸阳师范学院基础教育课程研究中心 安振平 712000 )

证明由a,b,c>0知，(b+c-a),(c+a-b),(a+b-c)中，至多有一个是非正数.

当(b+c-a),(c+a-b),(a+b-c)中，有一个是非正数时，所要证的不等式(记为(*))显然成立；

当(b+c-a),(c+a-b),(a+b-c)都是正数时，a,b,c构成一个三角形的三边长.

因为(ab+bc+ca)(a+b+c)≥9abc,

于是，要证明不等式(*)，只要证明

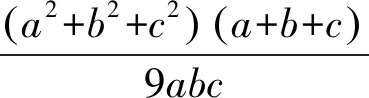
(b+c-a)(c+a-b)(a+b-c).(**)

应用三角形面积公式

知，不等式(**)等价于

a2+b2+c2≤9R2.

其中，R是三角形的外接圆半径，这是常见的不等式，故原不等式获证.

2464△ABC的内切圆O分别与边BC、CA相切于D、E，连AD，AD与圆O又交于P，连BP，CP.求证：∠BPC=90°的充要条件是AE+AP=PD.

(江苏无锡市第一中学 李广修 214031)

解如图，设AB切圆O于F，由切线长定理，

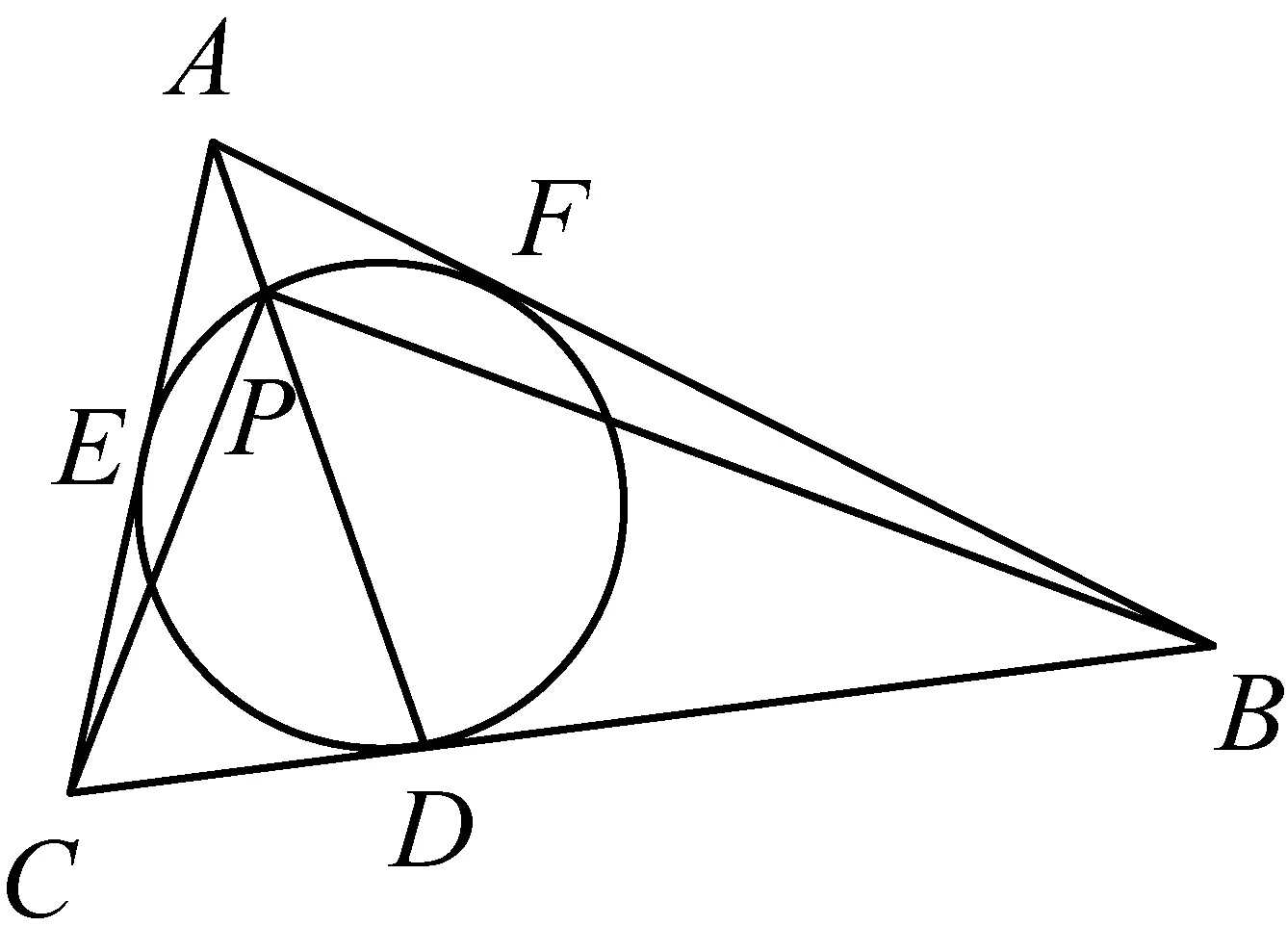
可设AE=AF=x，CD=CE=y，BD=BF=z，

又设AP=λAE，则AP=λx，

由切割线定理，得AE2=AP·AD，

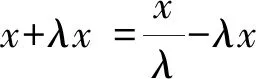
D在边BC上，对于△ABC，由斯特瓦尔特定理，

得AB2·CD+AC2·BD

=AD2·BC+BD·CD·BC，

将AB=AF+BF=x+z，CD=y，

BC=BD+CD=y+z，

代入上式，得(1-λ2)(xy+xz)=4λ2yz，

同理，P在边AD上，对于△ABD和△ACD，由斯特瓦尔特定理，

得BP2=z2+2(1-λ2)xz和

CP2=y2+2(1-λ2)xy，

从而，由勾股定理和勾股定理逆定理，

⟺(1-λ2)(xy+xz)=yz⟺4λ2yz=yz

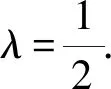
证毕.

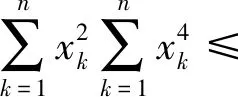
(山东省滨州市北镇中学 宋志敏 256600)

证明首先证明不等式

(1)

成立.事实上，利用Hölder不等式，可知

(2)

所以要证(1)成立，只需证明

再次利用Hölder不等式，可知

所以(1)成立.因此要证问题成立，利用(1)，只需证明

(3)

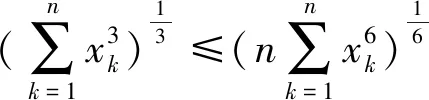
利用Cauchy不等式可知

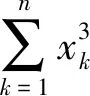
2019年2月号问题

(来稿请注明出处——编者)

(天津水运高级技工学校 黄兆麟 300456)

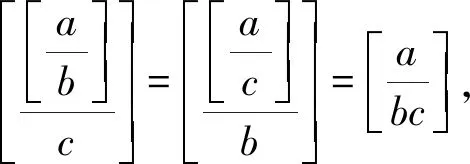
(贵州省织金县第六中学 邓波 552100)

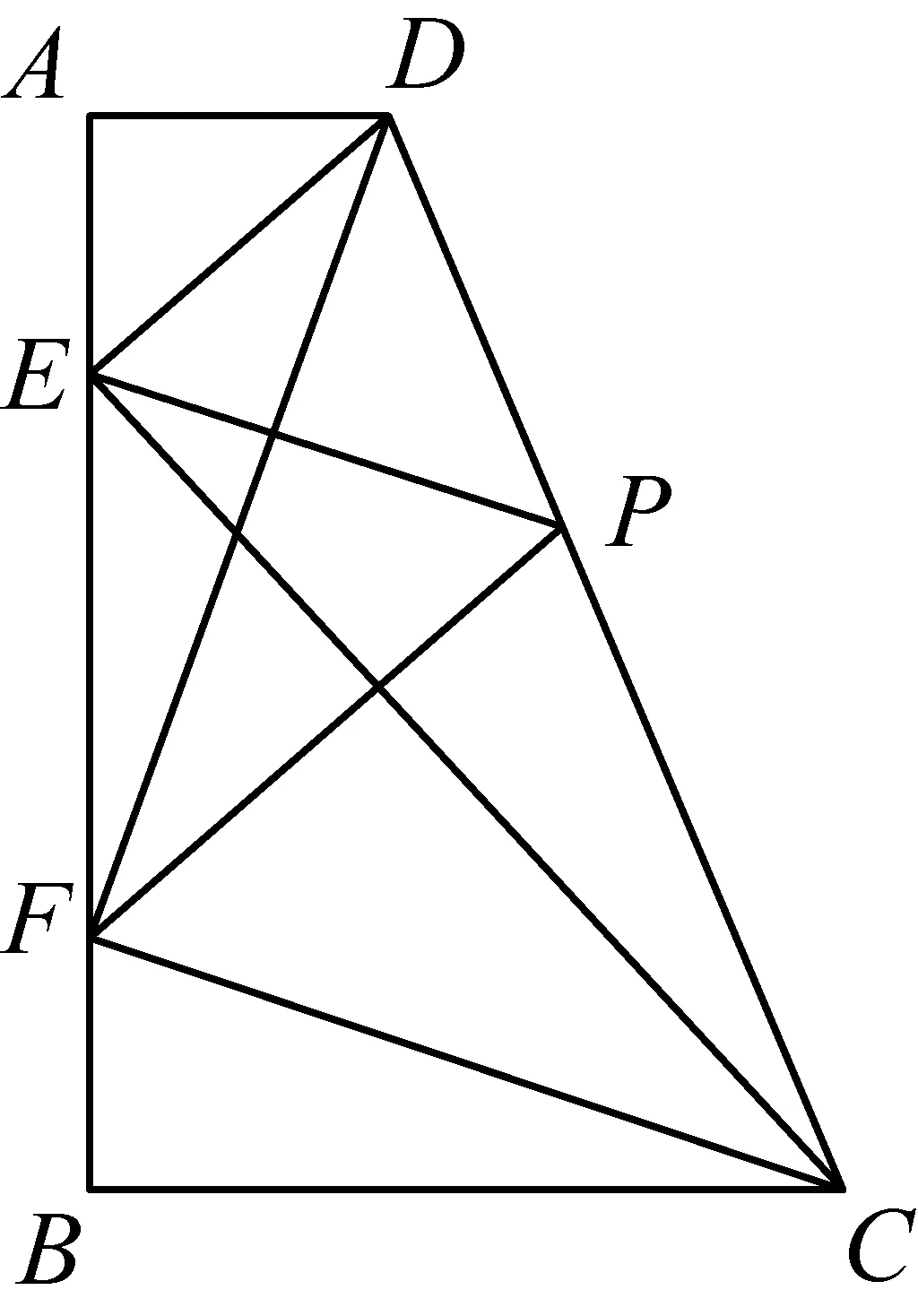
2468设不同的两点E，F在梯形ABCD的腰AB上， 且满足∠CED=∠CFD=∠ABC= 90°，在另一腰CD上求点P，使得AB≤PE+PF≤CD.

(河南辉县一中 贺基军 453600)

2469在△ABC中，设三边a,b,c上对应的高、角平分线、中线、旁切圆半径分别为ha,hb,hc；ta,tb,tc；ma,mb,mc；ra,rb,rc，∑表示循环和，求证：

(河南质量工程职业学院 李永利 467001)

(安徽省岳西县汤池中学 杨续亮 246620)