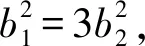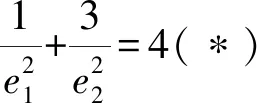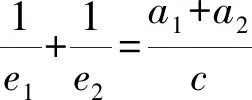基于思维培养的课堂“引导式”提问的若干原则——以一道圆锥曲线高考题的教学为例

毛浙东

(浙江省宁波市北仑中学 315800)

马卡连柯认为：教育技巧的必要特征之一就是随机应变的能力.当学生在课堂探究中思维受阻时，教师需要这种随机应变的能力，在短时间内提出一些建设性的意见，从而引导学生继续探索.这些意见往往通过提问的形式来呈现，我们把这种提问称为课堂“引导式”提问.

波利亚曾说：数学教学的目的在于培养学生的思维能力和思维品质.的确，数学是思维的体操，那么我们如何在课堂中对学生进行思维培养？亚里士多德给出了精辟的答案：思维从问题开始.众所周知，教师在教学中是起主导作用的，当学生在课堂上思维遇到困难而停滞不前时，教师抛出的“引导式”提问显得非常关键.良好的“引导式”提问，能启迪学生的思维，激发学生的学习兴趣，促进课堂有效探究，帮助学生进入深度学习，并在潜移默化中培养学生的数学思维品质.

那么，教师如何在课堂中开展有效的“引导式”提问？需要遵循哪些原则？ 下面笔者就结合一道圆锥曲线高考题的教学，来阐述基于思维培养的课堂“引导式”提问需要遵循的若干原则，希望能抛砖引玉.

1 “引导式”提问要顺应学生思维的轨迹

当学生的思维受阻时，教师要根据学生已有的思维轨迹进行顺势利导，切忌全盘否定学生的思路，这有助于学生获取成功的体验，建立学习的自信.

上课伊始，笔者抛出了如下一道高考题：

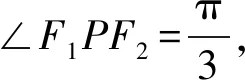
让学生经过几分钟的思考后，笔者请一位学生回答他的思路.

生1：我觉得本题应该会用到椭圆和双曲线的定义，可能还需要结合余弦定理来建立边角之间的关系，但是操作时我遇到了困难.

师(微笑)：那能将你想到的步骤具体说一下吗？

生1：设椭圆长半轴长为a1，双曲线的实半轴长为a2，不妨设|PF1|>|PF2|,由椭圆和双曲线的定义知

又由余弦定理知

|F1F2|2=|PF1|2+|PF2|2-|PF1|·|PF2|,

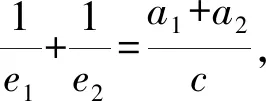
这时，笔者对其进行了如下的“引导式”提问.

提问1：你能否尝试用统一的字母来表示所有的量？比如都用a1,a2来表示？

由余弦定理知

此时学生思路再次受阻，于是笔者继续进行“引导式”提问.

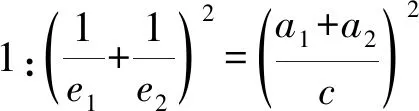
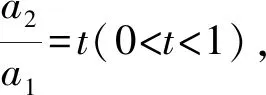
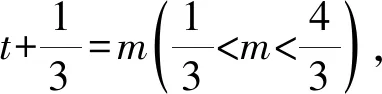
点评：在课堂中，学生的思维过程和教师课前准备的预案有时会“大相径庭”，这时教师的“引导式”提问一般有两种操作途径：如果教师判断学生的思路是不可行的，那么需要通过“引导式”提问将其纠正到正确的轨道上来；如果教师判断学生的思路是可行的，那也需要通过“引导式”提问 ，帮助学生在知识的最近发展区搭建脚手架，让学生顺利完成整个思维过程.但是无论是哪种操作途径，我们都应顺应学生的思维，循循善诱，切忌全盘否定或止步学生的思维.本环节的教学片段中，学生提出思路后，教师迅速判断出其思路具有可行性，于是通过两个“引导式”的提问，鼓励学生继续进行探索，并最终获得成功.学生的大脑由于受到正面积极的刺激，始终保持着兴奋的状态，学生的思维得到了锻炼和发展.

在解决问题的过程中，如果教师只是提供一些方法和建议，而解决问题的具体步骤都是学生自己想出来的，那么这些“方法和建议”是可迁移的内部帮助．内部帮助会指引解决问题的方向，提出解决问题的一般化方法与策略，而外部的帮助只对学生解决当前的问题发挥一种直截了当的作用，很难迁移到新的问题情境中.[1]在刚才的教学片段中，由于整个解题的“思路”是学生自己的，教师给学生提供的是内部的帮助，因此学生掌握的方法与策略具有可迁移性，此环节的学习是非常高效的.

2 “引导式”提问要培养学生思维的深刻性

为了让学生更透彻地看清问题的实质，特别是当问题已经获解之后，我们仍可以继续引导学生进行深入思考，从而培养学生思维的深刻性.如在本课中，笔者又对学生进行了如下的“引导式”提问 .

提问3：我们刚才用字母a1,a2来表示所有的量，那能否用其它字母来表示呢？

生2：我觉得也可以用PF1,PF2来表示.

又由余弦定理知

4c2=|PF1|2+|PF2|2-|PF1||PF2|,

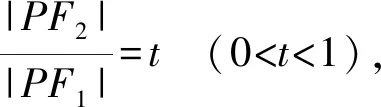
点评：数学学科的性质决定了学生的思维需要深刻性，而思维的深刻性又集中表现在智力活动中能深入思考问题，善于归纳概括，能抓住事物的本质和规律，开展系统的理解活动等. 教师在课堂中设置“引导式”提问时，提示语的指向性越隐蔽，那么对思维的挑战性越强，更能考查学生透过现象看本质的能力，因此在教学中通过合理设置“引导式”提问，有助于培养学生思维的深刻性.比如，本环节中的提问3相比上个环节中的提问1，指向性更隐蔽.提问1明确引导学生用字母a1,a2来表示所有的量，而提问3则没有任何这方面的暗示，而恰恰是这种“粗线条”的启发语，增加了思维的挑战性，也更能凸显问题的本质.学生通过对提问3的思考，深刻地体会到解决此题的关键是合理构造函数，至于构造怎样的函数，那就仁者见仁智者见智了.事实上，除了生1和生2所构造的函数之外，我们还可以选择其他变量来构造函数，同样可以解决问题.到此，学生的认知已经从“1”走到了“x”，从掌握某一种具体方法，上升到系统地掌握一类方法，从程序性知识的习得上升到策略性知识的习得，学生的思维达到了质的飞跃.

3 “引导式”提问要激发学生思维的创造性

为了让学生的思维能更开阔，教师有时需要“投一石而激起千层浪”，通过“引导式”提问，将学生带入广阔的思维海洋，激发学生思维的创造性.在本课例中，笔者就进行了这方面的尝试.

生3：由余弦定理可知

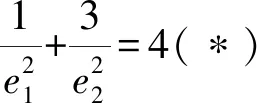
再由柯西不等式知

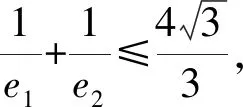
生4：我和生3一样先得到等式

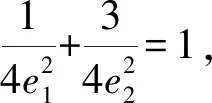
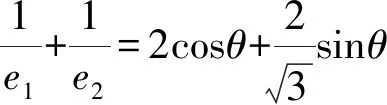
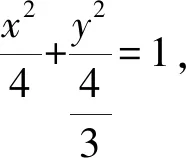
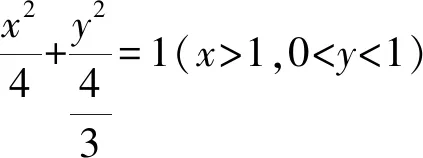
即x2+3y2=4(x>1,0

不妨设(x+y)2=x2+2xy+y2

≤x2+mx2+ny2+y2

=(m+1)x2+(n+1)y2,

点评：为了培养学生创新思维能力，我们要重视课堂中“引导式”问题的设计.弗赖登塔尔认为：每个人都有自己生活、工作和思考着的特定客观世界，以及反映这个客观世界的各种数学概念、运算方法和有关的数学知识结构.也就是说，每个学生都有自己独特的“经验系统”，这些“经验系统”是培育学生创造性思维的优质土壤，教师应针对学生的“经验系统”，通过“引导式”提问，让学生从已有的知识经验中“生长出”新的知识经验.当然，这些“引导式”提问入口要宽，学生容易上手 ，从而诱发学生思维的创造性.在“引导式”提问下学生往往能产生各种不同的想法，如在本教学环节中，生3通过柯西不等式进行放缩 ，生4巧妙地通过三角换元来减少字母个数，进而构造三角函数，使问题方便地得以解决，生5则通过换元，将条件转化为椭圆的一部分，利用数形结合来解决问题，生6则采用基本不等式进行放缩，同时结合了待定系数法，解法也很有新意.而这些创造性思维的产生，得益于教师引导学生得出关键的中途等式(*)式，从而激活了学生原有的知识经验，培养了他们的创造力.

4 “引导式”提问要破除学生的思维定势

学生在思考问题的过程中，往往会陷入思维的定势，此时教师应当帮助学生拨开迷雾，去开辟思维的新大陆，这有助于学生创新思维能力的培育.

提问5：刚才众多的解法都是先通过余弦定理得到中途等式(*)，是否只能用余弦定理得到(*)？

生7：设椭圆短半轴长为b1，双曲线的虚半轴长为b2，由椭圆和双曲线的焦点三角形面积公式知

提问6：本题是否一定要先得到中途不等式(*)，能否跳过这个过程？