点几何的教育价值

张景中 彭翕成

(1.华中师范大学国家数字化学习工程技术研究中心 430079； 2.广州大学计算科技研究院 510006)

1 争论从来都不断

初等几何在中小学数学教学中有着比较重要的地位.但如何处理这一内容，则存在不同看法.这些观点对于我们进一步认识初等几何，有一定的启发意义.

吴文俊先生认为[1]，“中小学数学教育的现代化是指机械化，而欧几里得体系排除了数量关系，纯粹在形式间经过公理、定理来进行逻辑推理，或者把数量关系归之于空间形式，这是非机械化的.中学应该赶快离开欧几里得，欧氏几何让位于解析几何.”吴先生的这一观点获得不少支持.因为欧氏几何的主要工具是全等、相似三角形，构造全等、相似三角形则常常需要费尽心思构造千变万化的辅助线，而花大力气掌握各种辅助线的技巧，对将来进一步的数学学习好像并没有太大的帮助.解析几何则使得数形结合更加紧密,用代数方法处理几何问题,思路清晰,有章可循,可操作性强.

王申怀先生则认为[2]，平面几何与解析几何的最大区别在于对几何图形研究所采取的方法不同，这两种方法可以互相补充，互相协调，它们对学生的数学思想方法、数学思维的训练作用并非完全相同.因此欧氏几何让位于解析几何的行动要慎重考虑.

当然还有其他的一些处理方式.譬如我们曾提出面积法体系[3]，这一体系被评论[4]为“有助于解决几何中一题一证的难点，但由于该体系的基础和表述方式与现有教材存在差异，影响了普及.目前更多的是为初等数学研究者，特别是数学竞赛研究者所掌握”.还有观点认为几何主要研究不变量，应以变换思想来处理，但也有人表示质疑[5]，认为在中学不宜过多强调几何变换.

如果我们把目光放得更远一点，就会发现类似的争论早已有之.解析几何创立之后，支持者众，但也有不同看法，认为解析几何虽在某些方面胜于欧氏几何，但有时计算繁琐,显得笨拙，且大量的计算都没有明显的几何意义，希望寻求能够更直接处理几何问题的代数方法.

莱布尼茨曾提出一个问题[6]：能否直接对几何对象作计算？他希望通过固定的法则去建立一个方便计算或操作的符号体系,并由此演绎出用符号表达的事物的正确命题.他认为理想中的几何应该同时具有分析和综合的特点,而不像欧几里得几何与笛卡尔几何那样分别只具有综合的与分析的特点.他希望有一种几何计算方法可以直接处理几何对象(点、线、面等),而不是笛卡尔引入的一串数字.他设想能有一种代数,它是如此接近于几何本身,以至于其中的每个表达式都有明确的几何解释：或者表示几何对象,或者表示它们之间的几何关系；这些表达式之间的代数运算,例如加、减、乘、除等,都能对应于几何变换.如果存在这样一种代数,它可以被恰当地称为“几何代数”,它的元素即被称为“几何数”.

沿着这一方向,数学家们开辟了“几何代数”的领域,孜孜不倦地寻求可能的合理的几何代数结构,试图实现莱布尼茨之梦.向量几何可看作是对莱布尼茨问题的初步回答.向量之间能进行加减运算,还可以进行内外积,且运算式都有明显的几何意义,有时利用向量处理几何问题也很方便[7].在向量几何之后，数学家们建立了更复杂的几何代数结构，此处略[6].

项武义先生认为[8]，自古到今,几何学的研究在方法论上大体可以划分成下述四个阶段：(1)实验几何:用归纳实验去发现空间之本质；(2)推理几何:以实验几何之所得为基础,改用演绎法以逻辑推理去探索新知,并对于已知的各种各样空间本质,精益求精地作系统化和深刻的分析；(3)坐标解析几何:通过坐标系的建立,把几何学和代数学简明有力地结合起来,开创了近代数学的先河；(4)向量几何:向量几何是不依赖于坐标系的解析几何，本质上是解析几何的返璞归真.

向量几何提出之后，也不断有专家提出新的想法.譬如莫绍揆先生认为，自线性代数兴起以来，直接从向量本身的性质(它可以说是几何性质)来处理问题，可以利用代数方法的长处，而处处符合几何直觉，有几何直觉的帮助.因此现在使用线性代数来讨论几何问题是大势所趋，无法阻挡.为克服向量几何的某些缺点且保持其优势,莫先生提出了更具物理意义的质点几何的理论和方法[9].他指出,向量本质上是几何变换,不是最基本的几何对象,因而希望建立以点为基础的几何代数体系.他借用力学的“质点”概念,把几何中的点看作是有位置无大小但有质量的东西,根据力学定律来对质点定义加法运算,然后以此为基础来研究几何.这种方法能对点直接进行运算,而且运算方便,运算表达式具有明显几何意义.

点常被认为是几何中最基本元素.点动成线，线动成面，面动成体，其他几何元素都可以由点扩展生成.因此希望建立以点为基本研究对象的几何体系也是很自然的想法.向量涉及两点，且自由向量可以在空间任意平移.为了简便以及排除不确定性，可在空间取定点O,称为原点,然后规定所有向量的始点都是原点,这样的向量称为位置向量，两个位置向量相等当且仅当它们的终点重合，每个位置向量的终点与空间的点是一一对应的.

我们在糅合向量几何、重心坐标、质点几何等体系的基础上，初步建构了点几何纲要[10]，其中包括了点的加法、数乘、两个点的内积、外积、三个点的外积及复数乘点等点几何中的基本概念，导出了近20条有关点运算的基本性质或基本公式，旨在建立一种几何代数系统，能够兼有坐标方法、向量方法和质点几何方法三者的长处而避免其缺点.本文将进一步阐述点几何在几何教学中的独特魅力，并辅以案例证明.

2 知识表示大不同

数学知识，特别是作为数学教育内容的基础知识，是客观世界的空间形式和数量关系的反映.同样的空间形式，同样的数量关系，可以用不同的数学命题、数学结构、数学体系来反映，正如从不同的角度给一头大象拍照一样，会得到十分不一样的照片，但它总是这一头象.只是有的反映方式便于学习、掌握、理解、记忆，有的则不然.不同的反映方式，尽管都是客观世界的正确反映，但教育的效果却会大不相同.譬如罗马数字的算术和阿拉伯数字的算术，尽管算题时得出同样的结果，但在教育效果上的差别是显而易见的.

因此，为了数学教育的目的，我们应当用“批判”的眼光审视已有的数学知识.这里的批判，当然不是怀疑这些数学知识的正确性，而是检查它在教育上的适用性.我们要用系统科学的现点，联系着前后左右的教学，联系着学生的心理特征与年龄特征，看一看，问一问，哪种反映方式较优？能不能找到更优或最优的反映方式.

为了认识空间图形的性质，我们可以学欧氏的《几何原本》，可以学“解析几何”或“三角学”，可以学“质点几何”，也可以学“向量几何”，甚至还可以创造新的几何体系.哪种方案能更快更好地完成这一阶段数学教育的任务呢？这需要我们仔细考察.

以中点为例加以说明.怎么表示点C是线段AB的中点？方法很多.

文字描述：点C是线段AB的中点.

图形描述(图1)：

图1

欧氏几何描述：

AC

=

CB

.但不要漏掉：

A

、

B

、

C

共线，否则只能说明点

C

在线段

AB

的中垂线上.

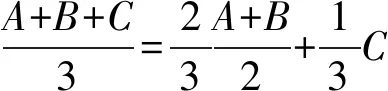
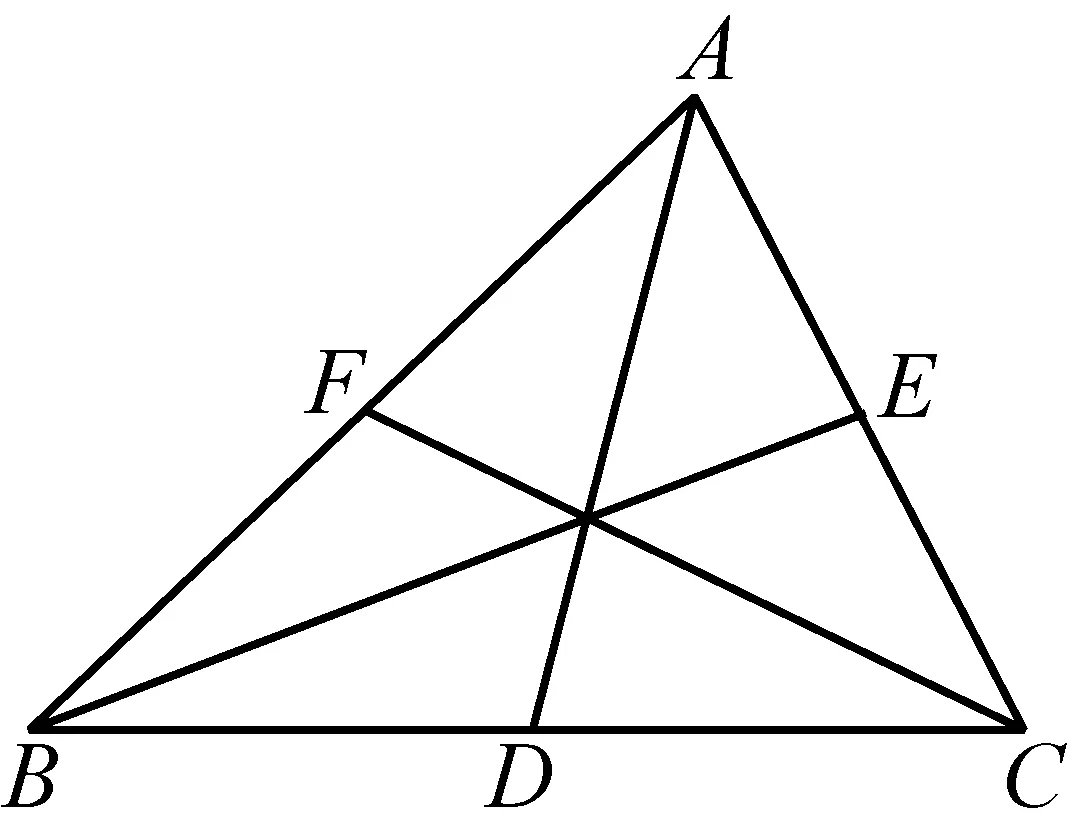
图2

两次使用中位线定理，可推出重心定理：

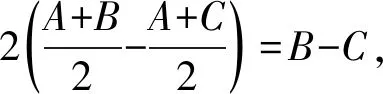
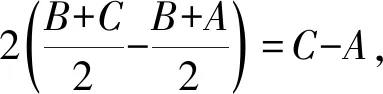
上述表示方式叙述简洁，推理清楚，且有明显的几何意义，适合在教学中使用.对比学术著作中的表述，两者天渊之别.在人工智能的经典著作《初等代数和几何的判定法》(A.塔尔斯基，J.C.C.麦克铿赛著)中有三角形重心定理的叙述，仅仅是叙述，还不包括证明.

(Ax)(Ay)(Az)(Ax′)(Ay′)(Az′){[～B(x,y,z)∧～B(y,z,x)∧～B(z,x,y)∧B(x,y′,z)∧B(y,z′,x)∧B(z,x′,y)∧D(x,z′;z′,y)∧D(y,x′;x′,z)∧D(z,y′;y′,x)]→(EG)[B(x,G,x′)∧B(y,G,y′)∧B(z,G,z′)]}

解释：任意六点x,y,z,x′,y′,z′，满足y不在x，z之间，z不在y，x之间，x不在z，y之间，(即x，y，z三点不共线)，且y′在x，z之间，z′在y，x之间，x′在z，y之间，且xz′=z′y，yx′=x′z，zy′=y′x，则存在点G，且G在x，x′之间，G在y，y′之间，G在z，z′之间.B(x,y,z)读作y在x和z中间，D(x,y;x′,y′)读作x到y的距离等于x′到y′的距离.

这种表达，像在初等代数的形式系统中一样，从原子公式经过使用否定词、合取词、析取词和量词构造出公式.通过这样形式化的表述，初等几何的语句即表达关于点的某个事实以及点与点之间的某种关系.

3 更多案例分析

在具体的解题实践中，我们发现，点几何不仅符合数学直观，能更方便地表达基本几何事实，而且有助于几何推理的简捷化.

AC2+BD2=AB2+BC2+CD2+DA2，

即AC2+BD2=AB2+BC2+CD2+DA2

⟺A+C=B+D,

即(B-A)2+(C-B)2+(D-C)2+(A-D)2-(C-A)2-(D-B)2=(A-B+C-D)2=0.

看似是代数变形，却对应着几何性质.这正是我们希望实现的将几何对象点当成数来计算.数与形进一步融合,正如希尔伯特所说：代数符号是书写的图形,几何图形是图像化的公式.

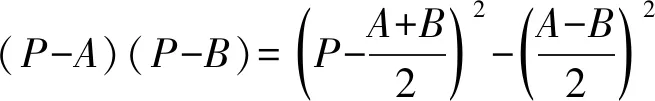
例1内心定理：△ABC中，AD、BE、CF是三角平分线，求证三线交于一点.

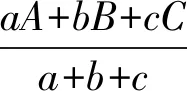
说明：此处用到角平分线比例定理.

例2垂心定理：△ABC中，若AH⊥BC，BH⊥CA，求证：CH⊥AB.

常规向量解答：

恒等式：(A-B)·(H-C)+(B-C)·(H-A)+(C-A)·(H-B)=0.

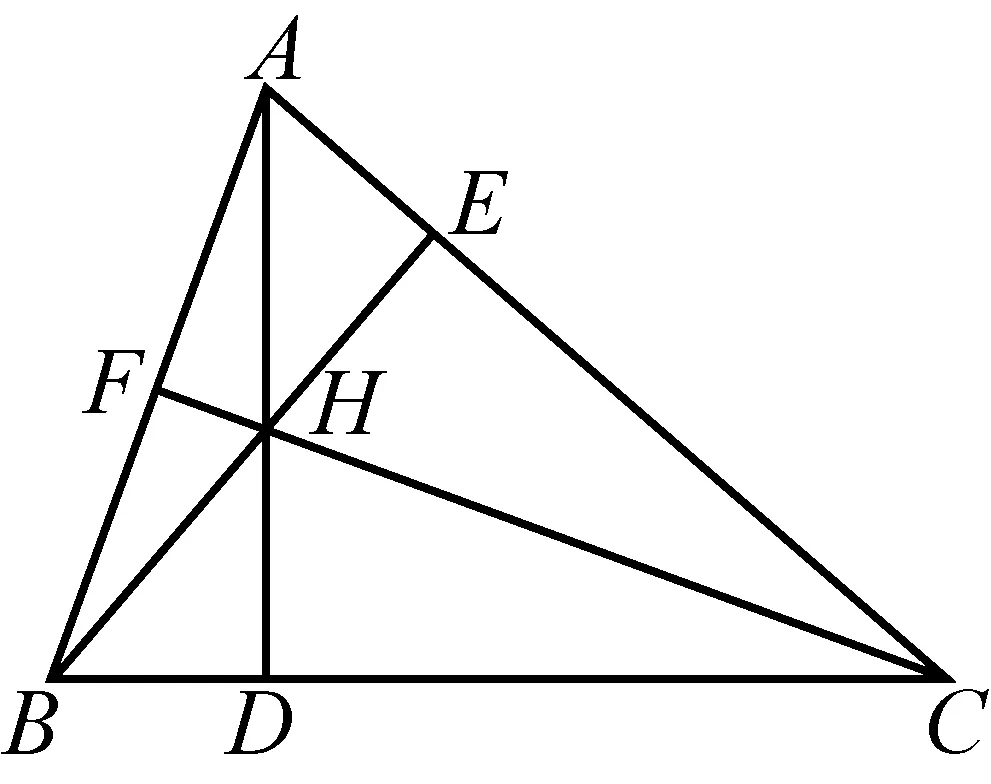
图3

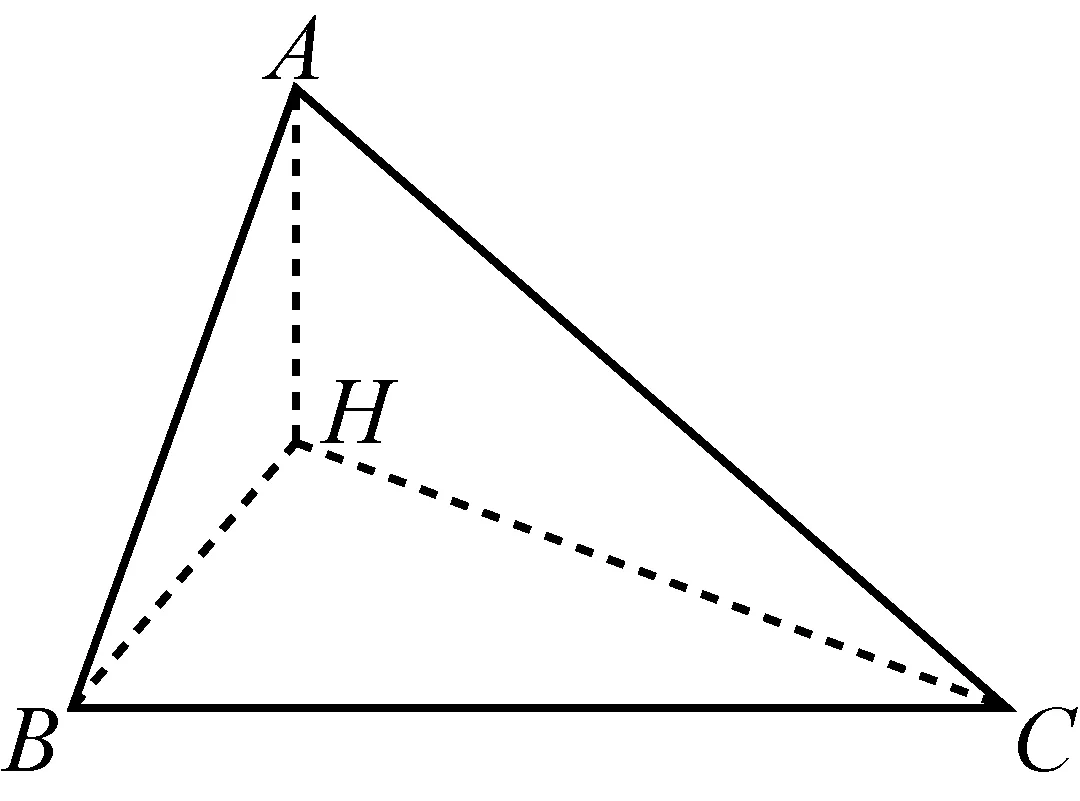
图4

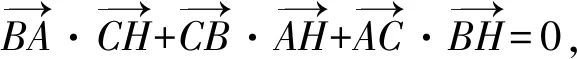
而这是显然成立的.因此得到另一种的向量解法：

例3外心定理：△ABC中，若点O在AB、BC的中垂线上，则点O在CA的中垂线上.

恒等式：

例2、例3两个恒等式中，其任意两部分为0，则第三部分必为0.

例4外心定理和垂心定理的相互转化.

如图5，传统证明中，要证△ABC的三高共点H，有时转化为证△DEF的三中垂线共点， 其中

四边形CABD、ABCE、BCAF是平行四边形.基于点几何的恒等式变形，是显然的.

由D=B+C-A、E=A+C-B、F=A+B-C得

⟺2(B-A)·(H-C)+2(C-B)·(H-A)+

2(A-C)·(H-B)=0.

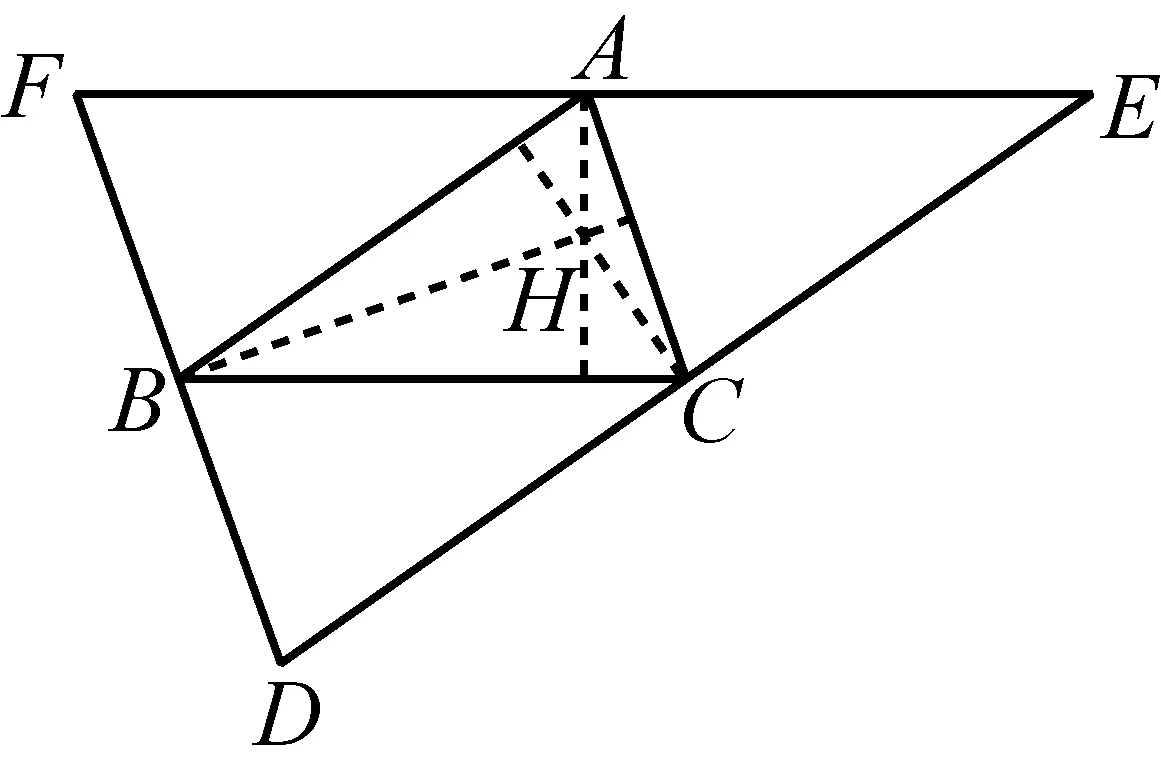
图5

例5欧拉线定理：△ABC中，外心O、垂心H、重心G三点共线.

根据垂心、外心的性质，

(A-B)·(H-C)=0，

(A-B)·(2O-(A+B))=0，

两式相加得(A-B)·(H+2O-(A+B+C))=0，

同理(B-C)·(H+2O-(A+B+C))=0，

(C-A)·(H+2O-(A+B+C))=0，

由于H+2O-(A+B+C)不能同时与三边垂直，

所以只能是H+2O-(A+B+C)=0，

若设A+B+C=3G，则H+2O=3G.

说明H、O、G三点共线，且HG=2GO.

4 结语

点几何、质点几何、向量几何都是几何的数学表示,本质上互通.作为3种几何语言,可以互译.如果规定从原点出发的向量叫点,向量几何就可以转化为点几何.如果规定两点差为向量,点几何就可以转化为向量几何.点几何最大的优势,在于用少量符号忠实地描绘几何事实,从而减少人的思维劳动.与向量几何、质点几何相比,点几何更简明,几何意义更丰富,表达力更强，数形结合融为一体.在点几何解题实践中，我们还发现了一种恒等式方法，目前已编程实现，通过验证600余道有难度的几何题(其中相当部分是竞赛题)，该方法效率高，可读性强，且能发现新的几何命题.关于点几何解题应用，我们将另文介绍.