高考力学平衡问题的解题方法

潘亚琼

【内容摘要】力学是高中物理教学的核心模块之一，更是高考中物理试题的热点和难点内容，由于这一部分内容属于物理知识的基础模块，但在知识的考查上又往往会结合许多科学思想与解题方法，因此与力学相关的考点近年来备受命题者的青睐。本文结合力学中平衡问题在高考中的应用，总结了解决此类问题的解题步骤与方法，旨在为学生在力学平衡问题上的学习提供一定的借鉴和参考。

【关键词】高考  力学平衡  解题方法

经过对近些年来高考中物理试题的研究，笔者发现，高考中与力学平衡问题相关的考点主要是共点力平衡的应用。解决此类问题，要求学生在对力学的基本性质定理牢固掌握的基础上，熟悉力的分解与合成方法，把握整体与隔离的物理思想。只有保证学生在基础、运算和思想方法上全面把握教材内容，学生在遇到此类题目时才能够做到有的放矢，游刃有余。

一、确定研究对象，进行受力分析

在力学平衡问题中，确定研究对象是做题的第一步，在研究对象的选取上，一般有两种方法：整体和隔离。一般情况下，如果题目中的研究对象是由多个物体组成，且整个系统的物理状态均相同，所要求解的是整个系统的外力，这时我们就可以采用整体法，将系统中的所有对象视为一个整体来研究。

确定了研究对象之后，下一步就是对研究对象进行受力分析，根据题目中所给定的研究情景，将研究对象的受力情况在受力图中表示出来。在进行受力分析时，首先要按照不同的性质力，如重力、弹力、摩擦力等对研究对象进行受力分析，以免漏掉某个力的存在。另外还要注意作出受力图之后，要注意回过头来检查此受力图是否可以使研究对象保持题目中所给出的状态。

二、分析平衡状态，确定求解方法

处于平衡状态下的物体和系统，其运动状态并不会发生改变，所以系统的加速度a=0，从而根据牛顿第二定律，物体或者系统所受的合力为零。因此，判断物体是否处于平衡状态就要判断其所受的合外力是否为零，换言之，所有处于平衡状态的系统或物体的合力都为零。

在平衡问题的求解中，如果系统是在两个力的作用下保持平衡，则可以直接利用二力平衡方程来求解。当出现三力平衡的情况时，则可以采用合成法来进行分析，根据受力平衡的条件，我们可以将物体或系统的受力情况转化到“力学三角形”中来求解，这也是在高中物理力学部分较为常用的一种解题方法。除了以上两种比较简单的受力情况，有些时候题目中还会出现多力平衡的情况，这一类问题的受力分析往往比较复杂，通常情况下我们会采用正交分解法来解决这一类问题。

三、典型例题分析，进行总结归纳

例1：合成法

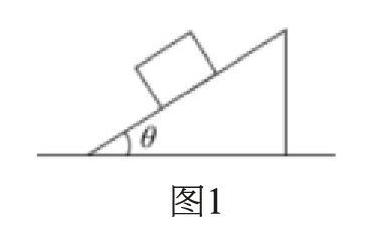
一个质量为m的物体静止在一个倾角为30°的斜面上，试求物体所受的支持力和摩擦力。

解析：通过对物体进行受力分析可得，斜面和小物块都静止，系统处于平衡状态，而小物块的受到重力、摩擦力和支持力的作用，属于三力平衡的情况。因此，解答此题首先要对小物块进行受力分析，作出其受力图，根据三力平衡状态下的物体，任意两个力的合力都与第三个力等大反向的关系，解出此题。需要注意的是，对小物体的受力分析必须要准确，很多学生会根据自己的感觉出现“加力”或者“少力”的情况。如在本题中，很多学生常常会感性地觉得小物块还会受到一个“下滑力”的作用，这是错误的。

例2：正交分解法

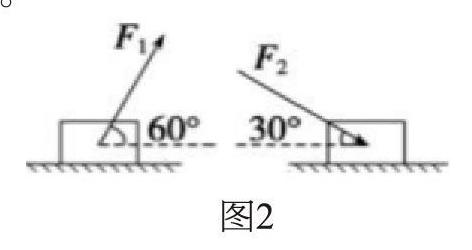
水平地面上放置了一个木块，如果对该木块施加一个与水平方向夹角为60°的拉力F1，木块恰好做匀速直线运动;当对木塊施加一个与水平方向夹角为30°的推力F2时，木块也可以做匀速直线运动。若F1与F2的大小相等，则该木块与地面的动摩擦因数为多少。

解析：分析此题可知，这是一道多力平衡状态的问题，首先依然是对研究对象进行受力分析，因为小物块做的是匀速直线运动，因此木块受到的合外力F=0。鉴于小物块的受力比较多，倘若按照之前的分析方法解题就会非常复杂，因此，此题我们可以采用正交分解法来解决。通过对F1和F2进行正交分解，得出小物块在平衡条件下的等式，再将等式进行联立，就很容易解出物块与地面之间动摩擦因数的值。

除了以上两种静止条件下的平衡状态以外，在高中物理力的平衡中还有一种平衡问题，就是动态平衡。动态平衡就是通过改变系统之中的某一个物理量，从而导致物体的状态发生缓慢的变化，可视为一种平衡状态。一般解决此类问题主要是应用解析法，通过对物体的平衡条件进行定量分析得出正确答案，但这种方法往往在运算的过程会比较复杂，需要学生具备良好的运算能力和严谨的物理态度。

总之，力学平衡问题在高中物理中具有举足轻重的地位，在高考试题中也往往具有一定的难度，但无论是静态平衡问题还是动态平衡问题，首先都需要进行准确的受力分析，再根据题目的类型选取恰当的解题方法。当然，其解题方法的灵活性和多样性还需要学生在平时的学习过程中多加总结，只有通过不断积累提升，才能在解题过程中做到镇定自若，游刃有余。

【参考文献】

[1] 郭骑兵. 剖析典型例题，理解力学平衡[J]. 文理导航（中旬），2017（12）：26.

[2] 赵云贺. 例析高中力学平衡问题的解法[J]. 高中数理化，2018（06）：23-24.

（作者单位：安徽省芜湖市无为县第二中学）