探寻类比规律 开启发现之门
2019-04-03席欣力
◎席欣力
高中数学新课程目标设置中,把“提高从数学角度发现和提出问题的能力、分析和解决问题的能力(简称“四能”)”、“不断提高实践能力,提升创新意识”作为课程目标。其中,发现和提出问题是创新意识的核心[1]。类比推理是合情推理的一种,是根据两个对象之间一部分属性相同或相似,从而推断出这两个对象另外的属性也可能相同或相似的思维形式,它是人类思维活动中最积极、最有创造性的成分。高中数学类比推理这类试题以类比思维为轴心,与数学方法、数学思想和数学基础知识相结合,是培养和发展学生核心素养的重要途径。以下分类例析。
一、变维类比
将三维空间的对象和二维或一维空间中的对象进行类比,这样的类比方法即为变维类比。此类问题以空间几何体与平面图形进行类比为主。
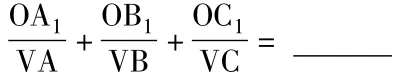
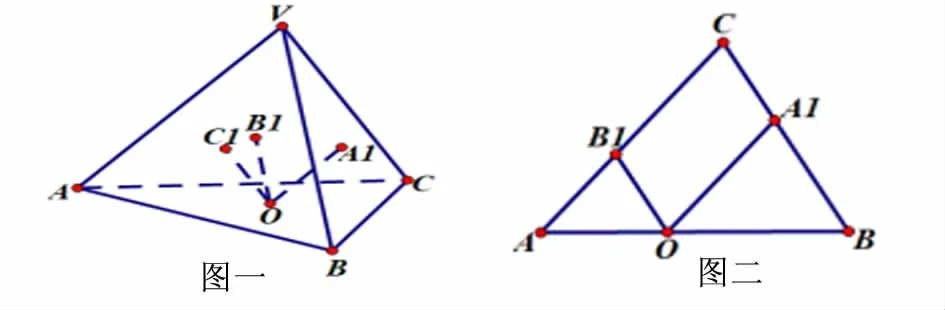

空间中,设平面 OA1VA∩BC=M,OB1VB∩AC=N,OC1VC∩AB=L,
则有 ΔMOA1∽ ΔMAV,ΔNOB1∽ ΔNBV,ΔLOC1∽ ΔLCV,
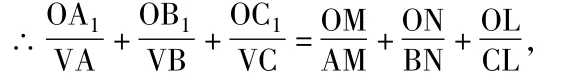
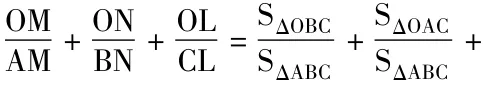
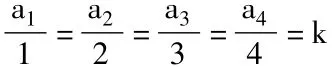
二、结构类比
某些待解决的问题没有现成的类比物,但可通过观察,凭借结构上的相似性等寻找类比问题,然后通过适当的代换,将原问题转化为类比问题来解决。常见的有函数的解析式与数列的通项公式之间的类比,等差数列与等比数列的类比,椭圆与双曲线的类比,解析几何中的两点间的距离公式及斜率公式与函数求值之间的类比等。
【例2】求值:sin280°+sin240°-sin 40°sin 80°
【解析】整体上看式子的结构和余弦定理相似,原式可改写成 sin280°+sin240°-2 sin 40°sin 80°cos 60°
而 80°+40°+60°=180°,80°、40°、60°可以看作一个三角形的三个内角,类比余弦定理可得解法。

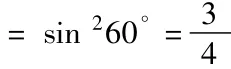
(2)O为抛物线 y2=2px(p>0)的顶点.
【解析】当M、N满足 EM⊥EN时,取M,N关于x轴的对称点 M′、N′,由对称性知 EM′⊥EN′,此时MN与M′N′所在直线关于x轴对称,若直线MN过定点,则定点必在x轴上.
设直线MN的方程为:x=my+t,
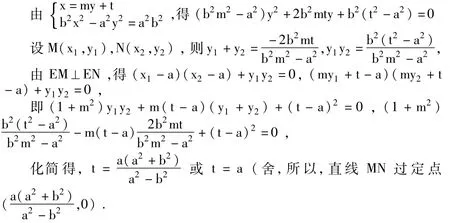
(2)在抛物线 y2=2px(p>0)中,若M,N为抛物线上的两点(都不同于原点O),且OM⊥ON,则直线MN过定点 (2p,0)
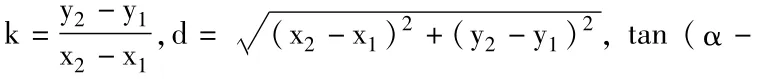
【变式2】数列{an}是正项的等差数列,若,则数列 {b}n也为等差数列,类比上述结论,写出正项的等比数列 {cn},若dn=_______,则数列 {dn}也为等比数列.
三、推广类比
推广类比就是将已知的、简单的命题,通过类比、概括、拓展推广到比原命题更一般化的命题。比如可将少元问题类比到多元问题,低次问题类比到高次问题,特殊问题类比到普遍问题等。推广类比可以扩大认知的范围,加深对知识的理解。
【例4】已知 a,b,c∈ R,且三次方程 f(x)=x3-ax2+bx-c=0有三个实数根 x1,x2,x3,
(1)类比一元二次方程根与系数的关系,写出此方程根与系数的关系;
【解析】(1)联想一元二次方程 x2-px+q=0的两根 x1,x2,满足x1+x2=p,x1x2=q,
x2-px+q=(x-x1)(x-x2),因而 x3-ax2+bx-c=(x-x1)(xx2)(x-x3),比较两边的系数,得 a=x1+x2+x3,b=x1x2+x2x3+x1x3,c=x1x2x3;
(2)f(x)=x3-ax2+bx-c,若 f(x)=0有三个两两不等实数根x1,x2,x3,则函数 f(x)有一个极大值和一个极小值,且极大值大于0,极小值小于0.
由已知得 f′(x)=3x2-2ax+b=0有两个不等的实数根 α,β,

【变式4】在直角坐标系中,不难得到“对于双曲线 xy=k,(k>0)上任意一点P,若点P在x轴、y轴上的射影分别为M、N,则必为定值k”;类比于此,对于双曲线,(a>0,b>0)上任意一点P,可以得出类似命题为_____________。
四、方法类比
某些陌生的、复杂的或抽象的问题,用常规的思路和方法很难解决,通过类比某些相关或相似问题的解答,在解题思路或思想方法上受到启发,从而实现原问题的解答。这种解题策略和思想方法的类比称为方法类比。
【例5】观察下面的解答过程:已知正实数 a,b满足 a+b=1,求的最大值.

请类比以上解题法,使用综合法证明下题:

【解析】由已知代数式的求值方法:先换元,再列方程,解方程,求解,可得代数式的值所求的式子也有无限重复的特点,类比可得解题方法:令,则两边平方得,=m2,即2+m=m2,解得m=2(-1舍去)。故答案为2。
【变式5】对于问题:“已知关于x的不等式ax2+bx+c>o的解集为(1,2),解关于 x的不等式ax2-bx+c>0”,给出了如下一种解法:
解析:由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于 x的不等式ax2-bx+c>0的解集为(-2,1)
在数学的学习中,思维的训练是本质。学习类比,掌握类比的方法和规律,就为发现问题解决问题“插上了翅膀”,善于类比,奇思妙想,我们就会发现很多繁难或新问题的神奇而精妙的解法,让我们享受数学的快乐。由于类比推理是由特殊到特殊的推理,它推理的逻辑根据是不充分的,带有或然性,具有猜测性,甚至是错误的,其正确性还须经过严格的逻辑推理加以论证,因而我们在运用时既要大胆尝试,又要严谨证明。
五、变式答案与解析

设直线MN的方程为y=k(x-c),代入椭圆方程得 (b2+a2k2)x2-2a2k2cx+(a2k2c2-a2b2)=0
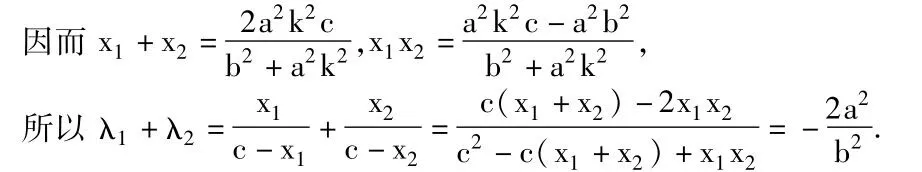
【解析】 对于双曲线xy=k(k>0)是我们熟悉的反比例函数,坐标轴是它的渐近线,其图像上任意一点P到渐近线的距离的积必为定值k,对于双曲线,它的渐近线为 bx+ay=0和bx-ay=0,其图像上任意一点P(x,y)在两条渐近线上的射影分别为M、N,则点P到渐近线的距离为,所以。
5.(-3,-1)∪(1,2)
【解析】由 ax2+bx+c>0的解集为(-1,2)得 a(-x)2+b(-x)+c>0的解集为(-2,1)发现 -x∈(-1,2),则 x∈(-2,1)
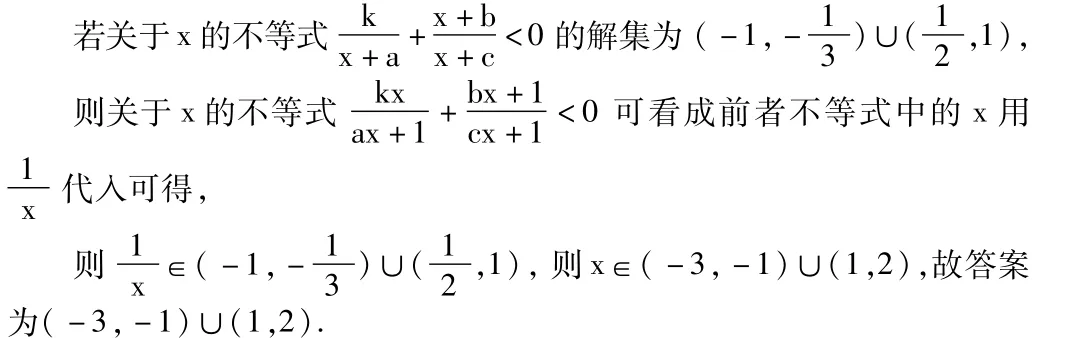
6.-1或2
【解析】类比上述解题思路,设f(x)=x3+x,则 f(x)在 R上单调递增,由x6+x2=(x+2)3+x+2,即f(x2)=f(x+2),∴x2=x+2,解之得,x=-1或x=2;所以方程x6+x2=(x+2)3的解为的解集为-1或2
