一类特殊曲线的渐近线问题

刘艳丽，孙皆宜

（唐山学院 基础教学部，河北 唐山063000）

1 渐近线的定义

定义1 若曲线D上的动点P沿着曲线无限地远离原点时，点P与某定直线L的距离趋于0，则称直线L为曲线D的渐近线。［1］

由以上定义可以得到三个常用的渐近线的定义：

（3）若函数y＝f（x）满足x→C（x→C＋或x→C－），有f（x）→∞，则曲线y＝f（x）有垂直渐近线x＝C。

2 y＝xsin和y＝x2sin的渐近线

2.1 曲线y＝xsin的渐近线x

由定义1易知：

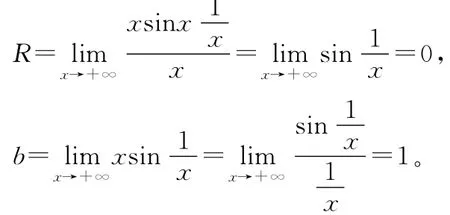
所以，曲线有一条水平渐近线y＝1．

用Matlab软件验证如下：

M－文件：

画图

2.2 曲线y＝x2sin的渐近线

由定义1求得

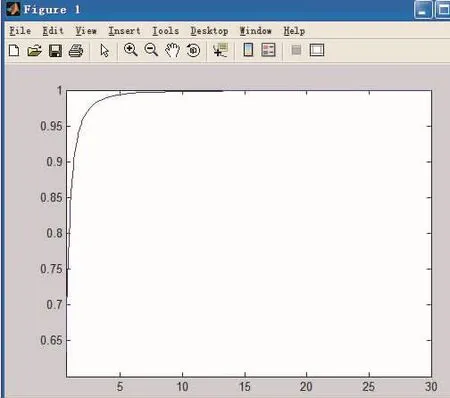
图1 y＝xsin1的水平渐近线x

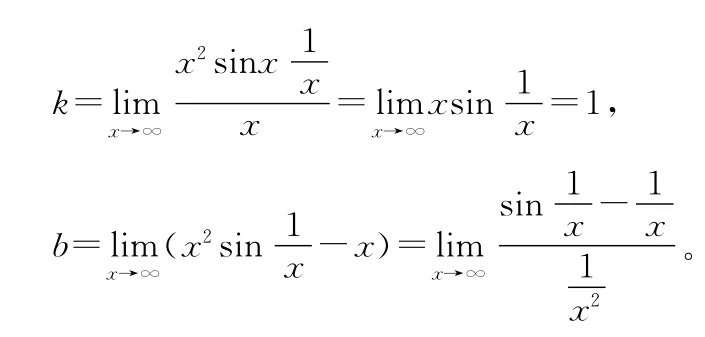
3 y＝x3sin的渐近线

对于y＝xnsin曲线族讨论n＝3的情况。

可以发现，在x→－∞时上述各极限也成立，所以不妨将定义2扩展成以下定义。

（3）如果曲线y＝f（x）既存在负方向Pn渐近线又存在正方向Pn渐近线且两渐近线相同时，就说曲线y＝f（x）存在Pn渐近线。

有了这一定义，就可以准确地说y＝x3sin存在Pn渐近线，且为P2渐近线，即。

4 需进一步研究的问题

考虑n＝1，n＝2时y＝xnsin1x的渐近线，可以发现在这两种情况下的渐近线实际上也可以归为Pn渐近线，n＝1时存在的水平渐近线，即为P0渐近线，方程为yP0＝1；n＝2时存在的斜渐近线，即为P1渐近线，方程为yP1＝x；而当n＝3时，存在P2渐近线，方程为yP2＝x2－16。

综上可知，曲线族y＝xnsin在n≤3时存在Pn 渐近线，且Pn渐近线的幂次与函数y＝xnsin中的幂次相比降低一次。那么，当n≥4 曲线族是否还存在Pn 渐近线？如果存在又具有哪些特点？这些渐近线能否用统一的形式表示出来？这些问题还有待于进一步探讨。

［1］ 华东师范大学数学系．数学分析［M］．北京：高等教育出版社，2007：64－65．

［2］ 刘仕田．Pn－渐近线［J］．高师理科学刊，2009（3）：10－12．