软土地基刚/柔性组合墙面加筋土挡墙离散-连续耦合数值模拟

陈建峰， 张 旭， 柳军修

(1. 同济大学 土木工程学院， 上海 200092； 2. 安徽建筑大学 土木工程学院， 安徽 合肥 230601)

刚/柔性组合墙面加筋土挡墙是一种新型加筋土结构，其分两个阶段修建：先构筑柔性墙面的加筋土挡墙，待地基沉降稳定后，再在柔性墙面外构筑刚性面板并与预埋在墙体内的连接件牢固连接，构成一个整体刚度很大的结构体.该型挡墙已在工程中得到成功应用，其能适应软土地基的大变形和不均匀沉降[1-4].

目前对软土地基上刚/柔性组合墙面加筋土挡墙的试验和理论研究还很有限.文献[5]对软土地基上刚/柔性组合墙面加筋土挡墙开展了离心模型试验，研究了其在自重及上覆荷载作用下的工作性状.文献[6-7]基于离心模型试验成果进一步开展了三维精细化有限差分数值模拟，研究了挡墙在上覆竖向荷载下的性状及受力机制，结果表明连接件可承担挡墙填土大部分的水平土压力，而上覆荷载引起的作用在组合墙面上的水平荷载可采用朗肯主动土压力计算，设计上，宜按连接件多承担水平荷载考虑.但是，有限差分方法模拟刚/柔性组合墙面加筋土挡墙具有局限性.首先，该型挡墙内部预埋了刚性连接件，其刚度与填土和筋材的刚度相差悬殊，使得材料接触面处的局部剪切应变很大，计算不容易收敛，不能进一步分析其稳定性机理；其次，刚/柔性组合墙面加筋土挡墙是分阶段建造的，其模拟过程是通过采用“空单元”生成刚性墙面再在地基固结沉降完成后“激活”的方法实现的，而地基固结沉降会使挡墙发生大变形，使得刚性墙面在“未激活”时就发生了较大的弯曲变形，那么模拟的挡墙分阶段建造过程将与实际不相符.

离散元法适于模拟碎散土(砂土、碎石土等)构筑物的大变形[8-9].但是，离散元法模拟软黏土需生成大量的颗粒，相比于有限元及有限差分方法计算效率要低很多.因此，结合离散元和有限元或有限差分方法的优点，采用离散-连续耦合数值方法，可对软土地基上的散体材料构筑物的变形及破坏机理进行研究[10-12].

本文基于笔者开展的软土地基上刚/柔性组合墙面加筋土挡墙离心模型试验[5]，建立离散-连续耦合数值模型，以离散颗粒流程序PFC模拟挡墙部分，以有限差分程序FLAC模拟软土地基，通过Socket I/O接口实现两者的耦合分析，以研究软土地基上刚/柔性组合墙面加筋土挡墙性状，并进一步探讨该型挡墙的内、外部稳定性.

1 离心模型试验概况[5]

离心模型试验原型的软土地基厚度为6.0 m，挡墙高度为3.0 m；在墙底与地基之间铺设0.6 m厚的砂垫层；柔性墙面采用反包形式，筋材共铺设5层，加筋长度为4.5 m；刚性墙面为强度等级C30的混凝土薄板，厚40 mm；预埋在墙体内的连接件共铺设3层，由拉杆与L形板组成，拉杆长度为2.25 m，间距为1.2 m，L形端板高度为12 cm.离心模型试验采用的模型率N=15，按模型率缩小后的模型尺寸如图1所示.

图1 离心模型试验示意图(单位：mm) Fig.1 Centrifugal model of reinforced soil retaining wall(unit: mm)

模型试验挡墙填土采用福建平潭标准砂，内摩擦角φ=27.3°，重度γ=16.2 kN·m-3.地基土为800目(粒径为0.001 8 mm)高岭土.模型筋材采用聚酰胺网，抗拉强度ft=13.5 kN·m-1，轴向刚度J=44 kN·m-1.刚性墙面根据抗弯刚度相似原则，选用厚度为2 mm的铝合金板.模型连接件拉杆用直径2 mm表面光滑的铜杆模拟，L形端板采用厚度为2 mm的铝合金板模拟.

离心模型试验过程分两个阶段：

(1) 第一阶段建立并运转柔性墙面加筋土挡墙.地基土采用含水量为100%的高岭土泥浆，在15g(g=9.8 m·s-2)离心加速度下充分固结制备.固结完成后，在高岭土地基上填筑柔性墙面加筋土挡墙至设计高度.然后，重新在15g下运转挡墙至地基沉降稳定后停机.

(2) 第二阶段建立并运转刚/柔性组合墙面加筋土挡墙.将刚性墙面与柔性墙面加筋土挡墙内的连接件用螺栓固定，在墙顶铺设2层5 cm×5 cm×2 cm(长×宽×高)的钢锭以模拟均布荷载，然后在15g下运转刚/柔性组合墙面加筋土挡墙，至地基沉降稳定.

2 数值模拟

2.1 模型建立

基于上述离心模型试验，建立离散-连续耦合数值模型.以离散元颗粒流程序PFC构建挡墙部分，生成粒径为1～2 mm的填土颗粒6 000余个，等粒径生成2 mm的筋材、连接件及刚性面板颗粒1 000余个，并等粒径生成4 mm的颗粒均匀分布在挡墙顶部，用来模拟离心模型试验放置在墙顶的钢锭荷载；以有限差分程序FLAC构建软土地基部分，在900 mm×400 mm范围内共划分40×20个网格，同时约束左右边界的水平方向位移，固定底部边界，得到的离散-连续耦合几何模型，如图2所示.

图2 挡墙离散连续耦合几何模型 Fig.2 Coupling of discontinuous-continuous geometrical model of reinforced soil retaining wall

2.2 材料参数

填土细观参数通过对平潭标准砂直剪试验离散元模拟确定.建立尺寸大小为400 mm×150 mm的直剪试验模型，法向应力取50、100、150、200 kPa，得到抗剪强度曲线见图3.由图3可见，模拟得到的内聚力c=0，内摩擦角φ=26.3°，与通过室内直剪试验测得的平潭标准砂内摩擦角27.3°基本一致.所选取的细观参数见表1.

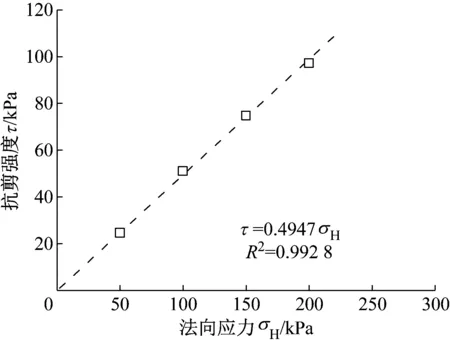
图3 挡墙填土直剪试验模拟曲线 Fig.3 Computed curve of direct shear test of fill

本文采用PFC中平行黏结(parallel bond)模型模拟筋材，通过对筋材宽条拉伸试验离散元模拟确定其细观参数，数值模拟的筋材拉伸力-伸长率关系曲线(图4)与筋材宽条拉伸试验结果吻合很好，其细观参数选择见表1.

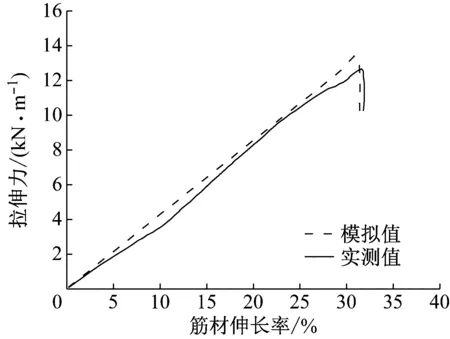
图4 筋材拉伸试验模拟和试验曲线比较 Fig.4 Comparison of computed and measured tensile curves of geogrid

挡墙刚性墙面主要受弯曲作用.采用平行黏结模型建立刚性墙面模型，其细观参数根据三点抗弯试验离散元模拟确定.挠度曲线与理论值对比如图5所示，两者基本一致.

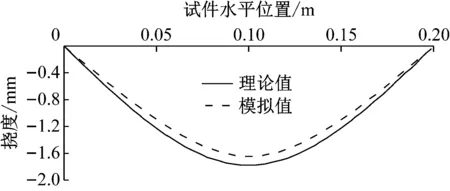
图5 刚性面板挠度曲线对比 Fig.5 Comparison of deflection curves of rigid wall face

如图1所示，连接件拉杆水平向为等间距布置，需要将其等效成连接件墙，以进行二维平面应变分析.假定连接件墙的厚度与铜制连接件杆的直径相同，则等效模量Ew为

Ew=Ebar+Es(1-ar)

式中：Ew、Eb和Es分别为连接件墙、铜制杆件和填土的模量；ar为一排连接件的铜制杆件的面积置换率.其中铜制杆件的模量Eb=108 GPa，面积置换率ar=1/40，填土模量Es=20 MPa.

按平行黏结模型建立连接件模型，其细观参数根据拉伸试验离散元模拟确定.拉伸试验结果如图6所示.其拉伸模量E=2.93 GPa，与连接件墙的模量Ew=2.7 GPa基本一致.连接件细观参数如表1所示.

表1 挡墙模型细观参数Tab.1 Microscopic parameters of reinforced retaining wall

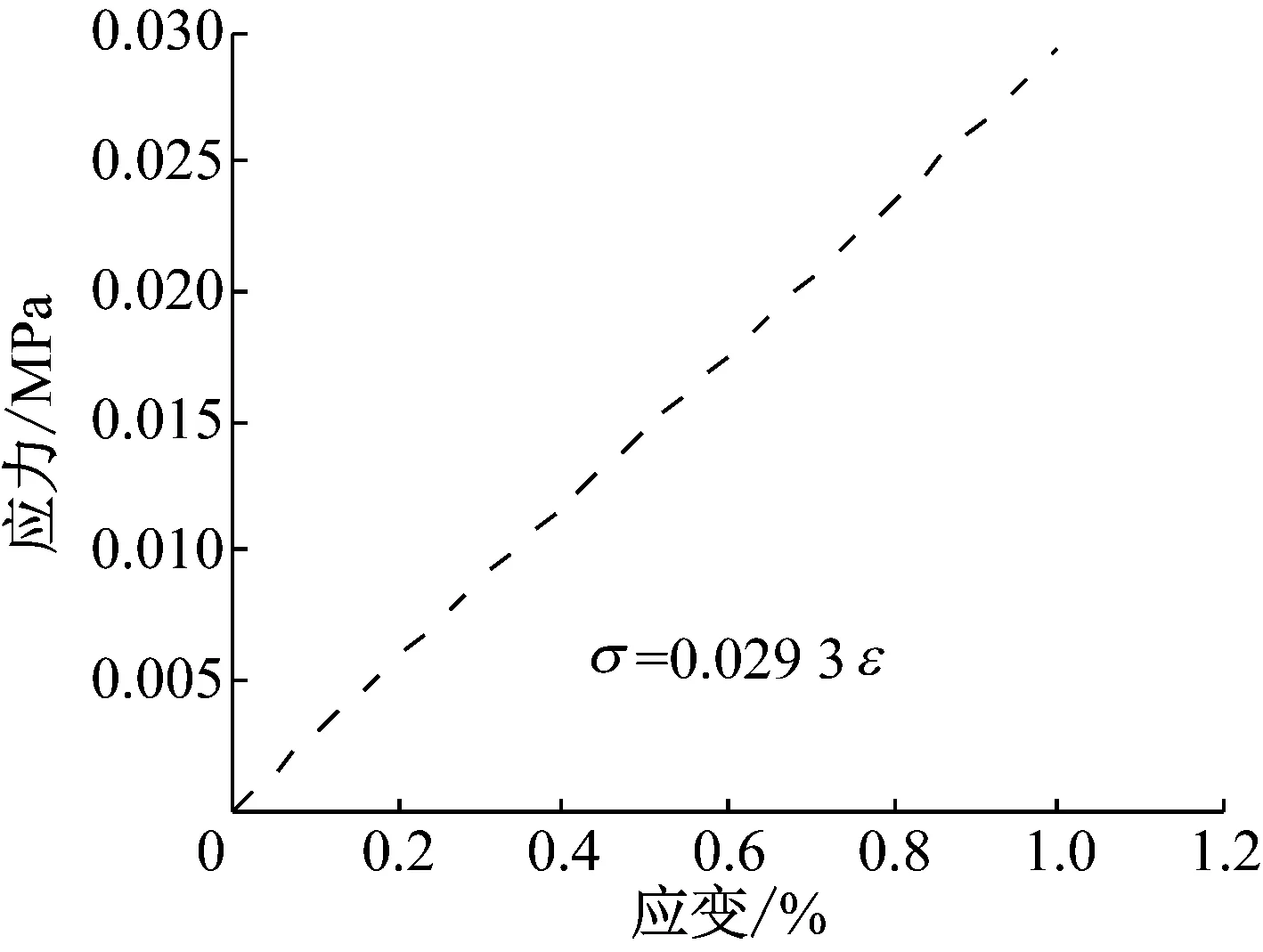
图6 连接件拉伸试验曲线 Fig.6 Computed tensile curve of anchor

墙顶钢锭荷载以粒径4 mm的颗粒模拟，赋予颗粒的密度为48 000 kg·m-3，与离心模型试验中作用在墙顶的均布荷载一致.

地基土采用摩尔-库伦模型模拟，其参数取值如下：弹性模量E=6.0 MPa，泊松比ν=0.3，黏聚力c=2.1 kPa，内摩擦角φ=10°.

2.3 模拟过程

数值模拟过程与离心试验过程相同，分两个阶段：第一阶段通过离散颗粒流程序PFC生成填土、筋材和连接件，建立柔性墙面加筋土挡墙，同时采用FLAC生成地基土；然后分别打开FLAC和PFC程序的Socket I/O接口，以FLAC为服务器，PFC为客户端建立数据交换通道，将FLAC中耦合边界节点速度传递到PFC模型边界中，PFC模型再将边界应力传递至FLAC模型边界，在15g离心加速度下循环计算至沉降稳定.第二阶段生成刚性墙面并与预埋连接件连接，然后生成墙顶均布荷载，继续施加15g的离心加速度，耦合计算至沉降稳定，耦合方式与第一阶段相同.

3 计算结果分析

3.1 挡墙变形

图7是数值模拟与离心模型试验在两个阶段的挡墙变形对比图.图7中离心模型试验图片上绘出数值模拟试验得到的挡墙筋材、墙底地基表面及刚性墙面变形轮廓线(虚线).由图7可见，数值模拟与离心模型试验结果基本吻合.挡墙在自重及上覆荷载作用下发生了显著沉降和不均匀沉降，但挡墙墙面仍基本保持直立，显示该型挡墙具有很好的适应软土地基大变形的能力.

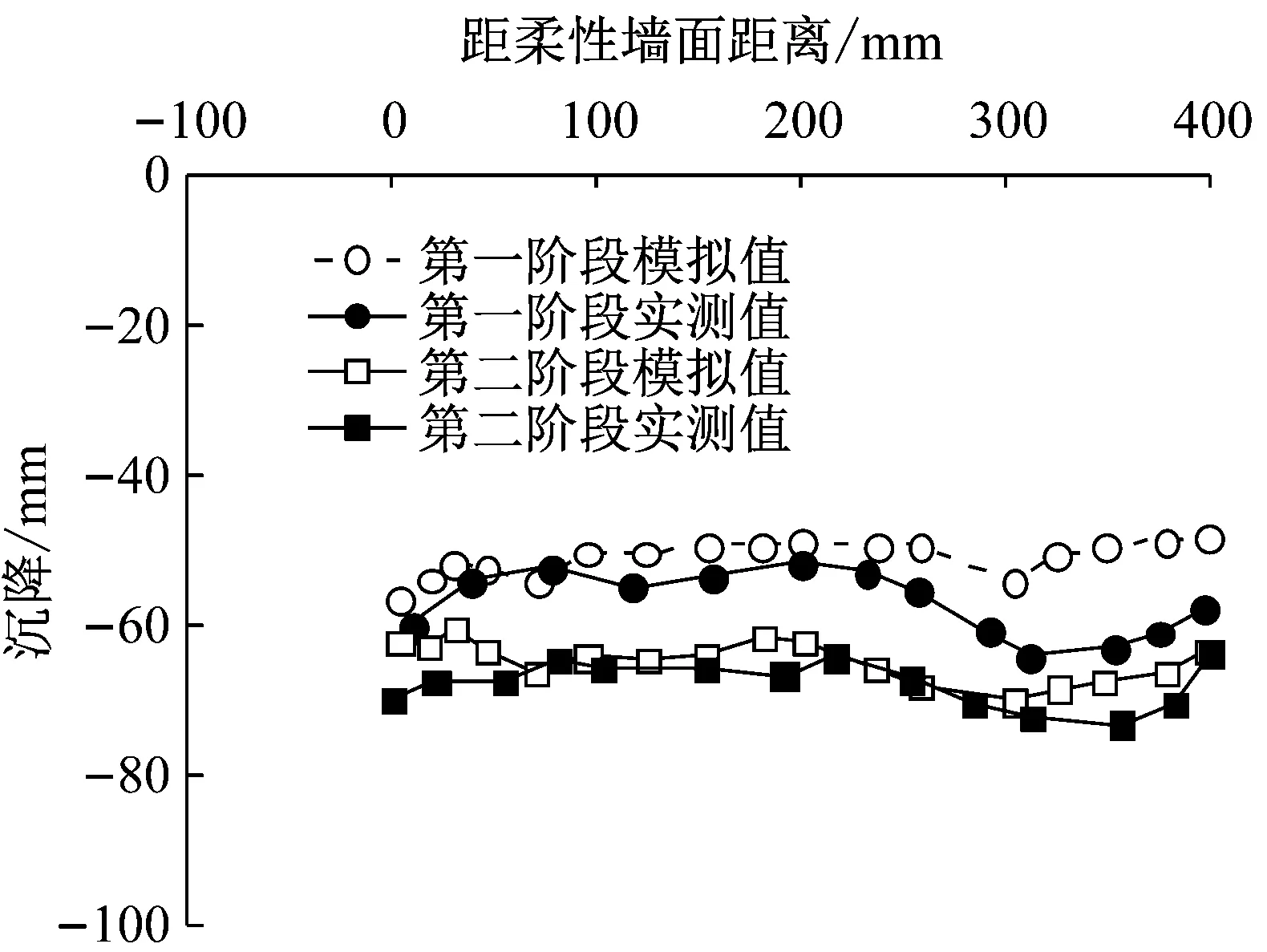
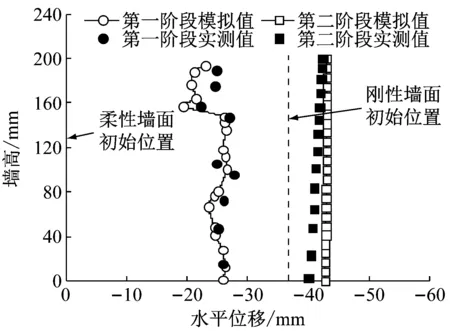
图8是数值模拟与离心模型试验在两个阶段的墙底地基表面沉降、墙顶沉降及墙面水平位移的对比图，其中第一阶段的挡墙变形是挡墙自重应力作用下产生的，而第二阶段的挡墙变形是在第一阶段挡墙自重应力作用下产生的变形基础上叠加了上覆荷载(45 kPa)作用下产生的变形，另外实测的挡墙变形是通过对离心模型试验同步摄像机拍摄的照片进行图像分析得到的.由图8可见，数值模拟和离心模型试验的挡墙变形结果基本吻合，挡墙在第二阶段上覆荷载作用下相对第一阶段所产生的沉降及墙面水平位移增量均显著小于第一阶段挡墙自重应力下的变形量，这是由于第二阶段连接件与刚性墙面组成的结构体整体刚度大，能显著减小挡墙变形；两个阶段的地基表面均发生显著的不均匀沉降，墙趾前缘的地基发生隆起，最大沉降发生在挡墙加筋区中部连接件末端位置(图8a)，这是由于此处发生应力集中所致；两阶段的加筋区墙顶沉降均比较均匀，而在加筋区后缘发生凹陷，该处的墙顶沉降也是最大的(图8b)；第一阶段柔性墙面的水平位移沿墙高分布基本均匀，其中部和下部墙面的水平位移均约27 mm，只有墙顶部位的水平位移略小，而第二阶段在上覆荷载作用下刚性墙面墙顶和墙底水平位移相对其初始位置的增量分别仅为5 mm和3 mm，墙面仍基本保持直立(图8c).

3.2 基底应力

图9为模拟和实测的两个阶段的墙底地基表面竖向土压力，其中第一阶段的土压力是挡墙自重应力引起的，第二阶段的土压力是挡墙自重及上覆荷载共同作用引起的.由图9可见，这两个阶段，离心模型试验在实测点处的土压力与模拟值基本吻合；数值模拟的竖向土压力均呈不均匀分布，加筋区范围内的竖向土压力大于非加筋区，且均在连接件末端处最大，这是由于连接件埋置范围内的墙体整体刚度较大，荷载作用在刚度突变的位置引起了明显的应力集中，故使得地基表面沉降在此处最大，如图8a所示.

数值模拟

离心模型试验 a 第一阶段挡墙变形对比

数值模拟

离心模型试验 b 第二阶段挡墙变形对比图7 离心模型试验和数值模拟变形对比 Fig.7 Comparison of computed and measured deformation of reinforced wall

3.3 刚性墙面弯矩

图10为第二阶段上覆荷载作用下模拟和实测的挡墙刚性墙面弯矩沿墙高分布，本文中负弯矩表示刚性墙面外侧受拉，正弯矩表示刚性墙面内侧受拉.由图10可见，数值模拟的刚性墙面弯矩与离心模型试验监测点的结果基本一致，最大的弯矩均在墙中处，为外侧受拉，墙顶与墙底处的弯矩值均较小，为内侧受拉.

试验挡墙在0、0.08和0.16 m高度墙面处设置了可以提供侧向约束的连接件，相当于作用在刚性墙面的集中力，根据结构力学原理，刚性墙面弯矩应在集中力作用的位置发生突变.如图10所示，本文数值模拟结果符合结构力学原理.

4 挡墙内、外部稳定性探讨

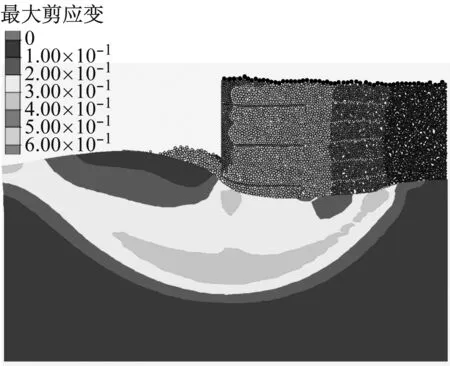
上述软土地基上刚/柔性组合墙面加筋土挡墙模型在15g时发生了显著变形，但是挡墙整体仍很稳定.为探求挡墙的稳定性，继续对离散-连续耦合数值模型施加加速度直至35g，使得挡墙产生明显的滑移破坏.

图11为加速度为35g时挡墙变形及地基剪应变增量云图.由图11可见，地基中产生了明显的圆弧滑移面，滑移面经过挡墙底层筋材后缘，挡墙随地基土转动，呈明显后仰趋势.

由于挡墙颗粒流模拟不能输出剪应变增量，但可以获得总位移，为了显示挡墙颗粒流滑移面，在挡墙和地基变形前网格坐标系统基础上，绘制挡墙和地基的总位移等值线云图，如图12所示.由图12可见，过挡墙底层筋材后缘有一平直破坏面，其与水平面的夹角约为45°+φ/2≈59°(φ=27.3°，为填土的内摩擦角)，表明该破坏面即为朗肯破坏面，其与地基中过底层筋材后缘的圆弧滑移面一起组成挡墙外部稳定深层滑移破坏面.

软土地基上的加筋土挡墙容易出现上述深层滑移的外部稳定性问题[13-14].文献[13]开展了深厚软土地基上筋材长度10 m、间距0.5 m的加筋土挡墙现场试验，该挡墙在堆载高度至7.6 m时发生了经过加筋后缘的外部稳定深层滑移破坏；文献[14]对该挡墙进行了有限元数值模拟及稳定性分析，发现即使将筋材加长至20 m，挡墙依然发生外部稳定的深层滑移破坏.这是由于实际挡墙所采用的加筋间距一般不大，而筋材强度和刚度较大，使得挡墙加筋体相对软土地基的刚度要大很多，变形时整体性好，不容易产生切过筋材的内部破坏面.

a 地基表面沉降

b 墙顶沉降

c 墙面水平位移 图8 两阶段的挡墙变形 Fig.8 Deformation of reinforced wall in two stages

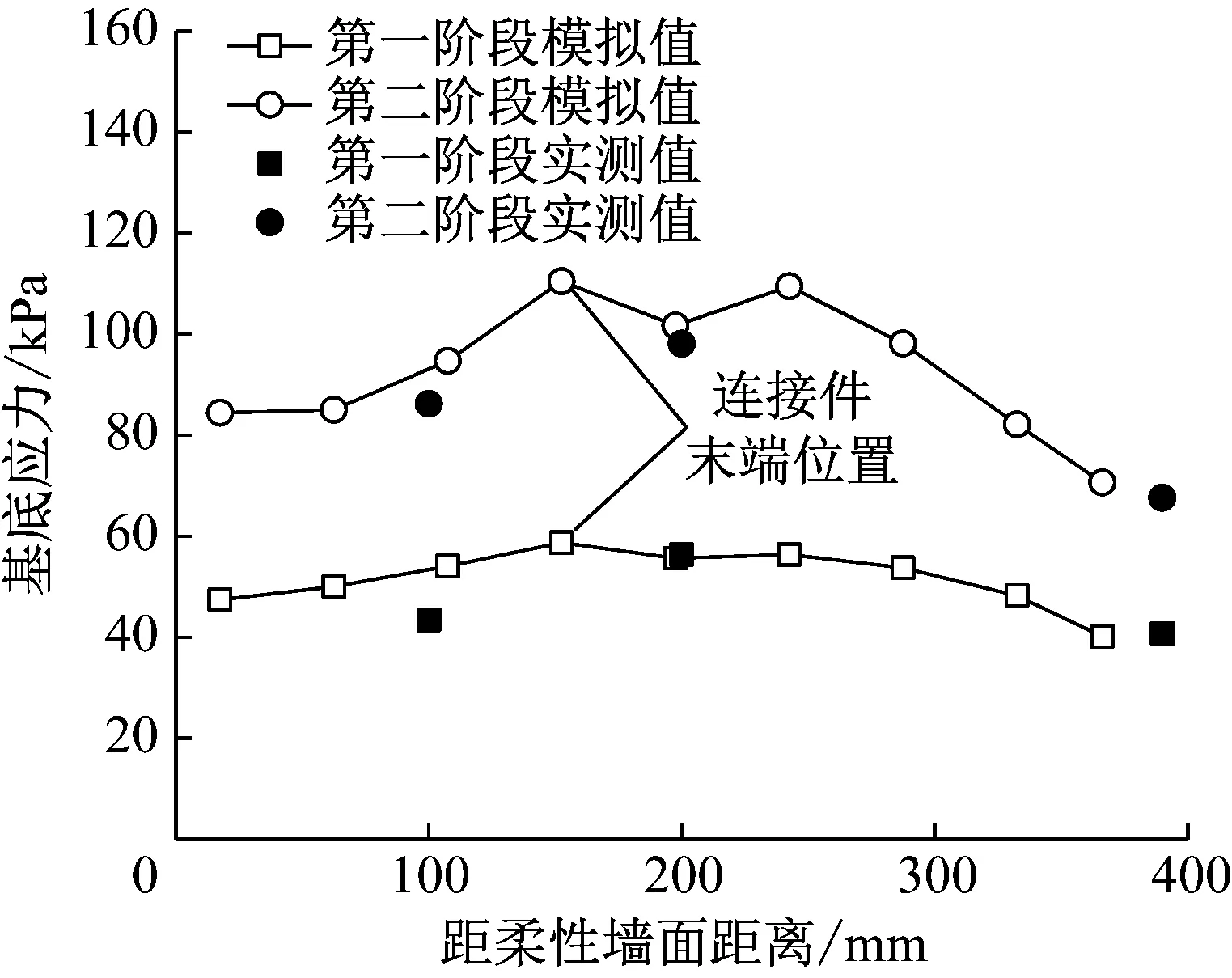
图9 两阶段的墙底地基表面竖向土压力 Fig.9 Vertical earth pressures of foundation surface in two stages

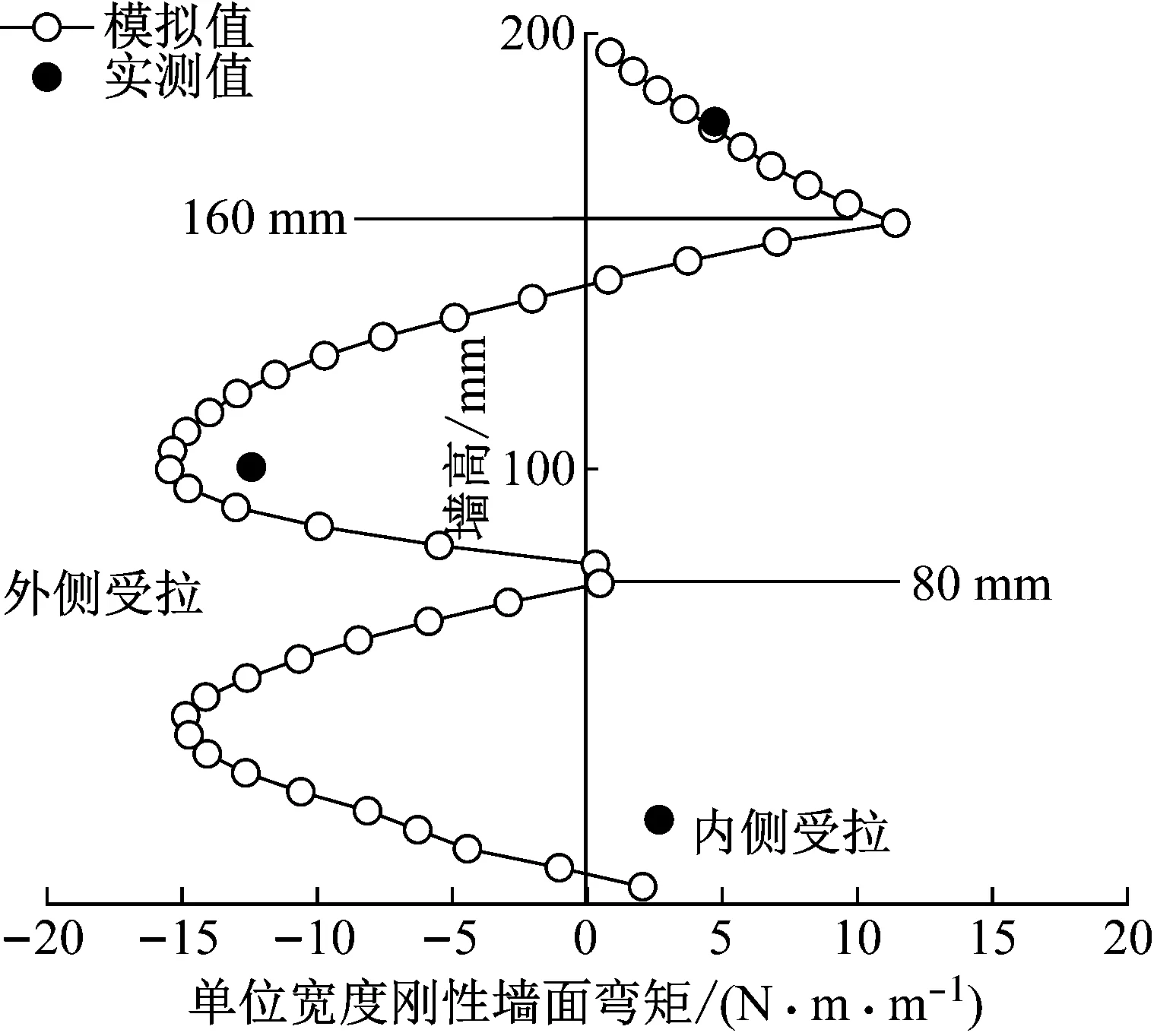
图10 刚性墙面弯矩沿墙高分布 Fig.10 Distribution of rigid facing moments along wall height

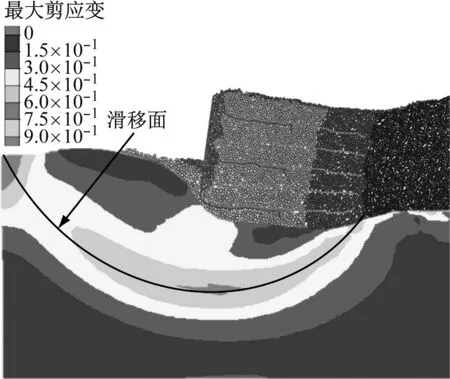
图11 挡墙变形及地基剪应变增量云图Fig.11 Deformation of retaining wall and contour of maximum shear strain increment of foundation

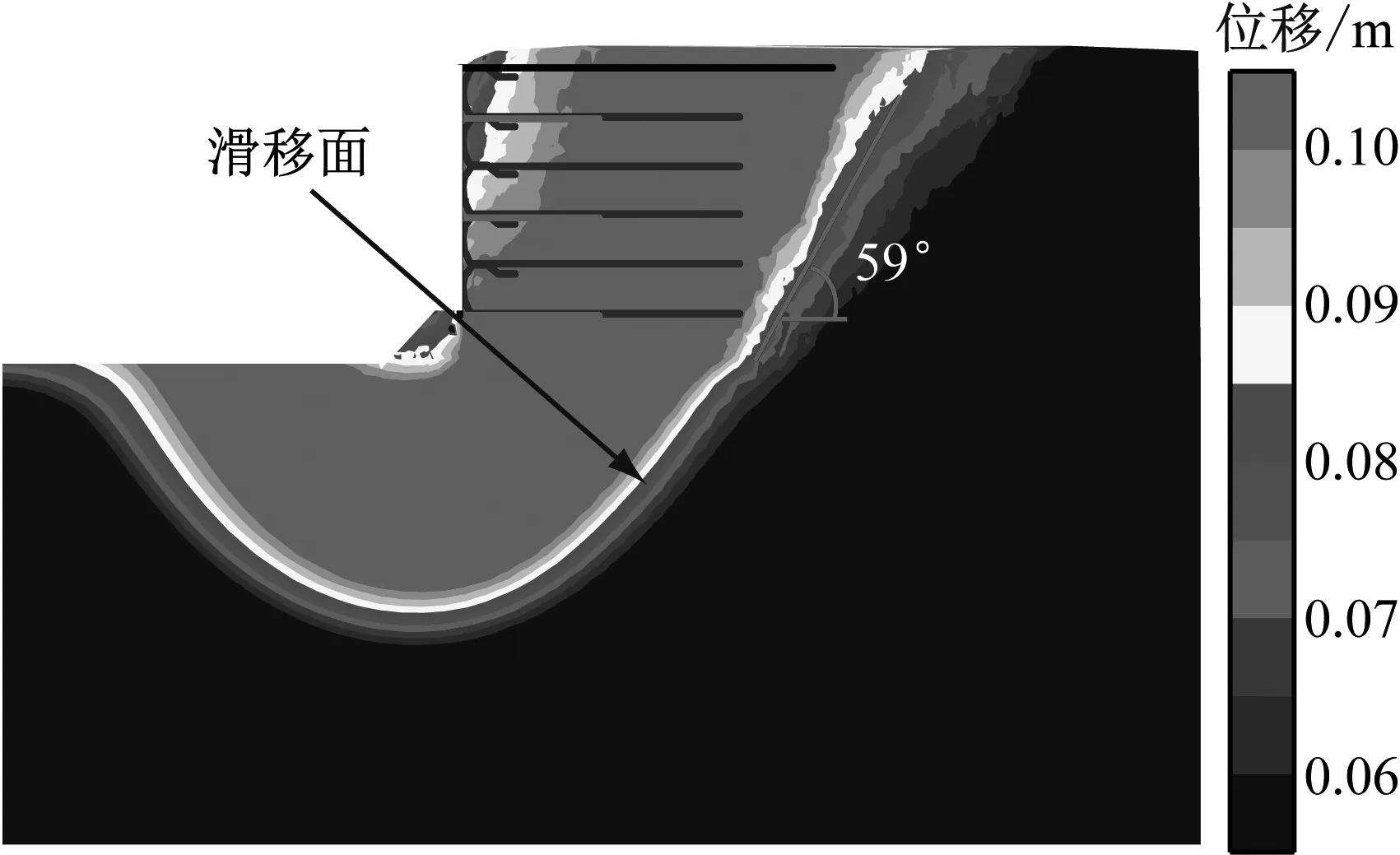
图12 模型外部破坏的位移等值线云图 Fig.12 Displacement contour of the model in external failure

然而，加筋土挡墙的内部稳定性是工程设计计算所必需的.已有的刚性地基上单一墙面加筋土挡墙的内部破坏面为一过墙趾的朗肯面，但是对于软土地基上刚/柔性组合墙面加筋土挡墙内部破坏面的研究还未见报道.这里采用逐步降低筋材强度的办法来探讨软土地基上刚/柔性组合墙面加筋土挡墙内部稳定性.当筋材强度降低至1.5 kN·m-1时，上述离散-连续耦合数值模型在35g加速度下产生了内部破坏.图13为35g时5 000、10 000、40 000计算步的挡墙变形与地基最大剪应变增量云图.由图13可见，在5 000计算步时，挡墙产生明显变形，挡墙刚性连接件范围内的填土出现比较明显后仰现象，挡墙底部以上的第1、2层筋材在底层连接件后缘处断裂，同时地基中开始形成过底层连接件后缘的圆弧滑移面；在10 000计算步时，地基中剪应变增量和挡墙变形继续增大，挡墙第3、4层筋材紧接着发生断裂；40 000计算步时，地基中剪应变增量进一步增大，地面隆起显著，挡墙顶层筋材在末端拔出破坏，形成挡墙内过底层连接件后缘的平直滑动面，与地基中的圆弧滑移面贯通.

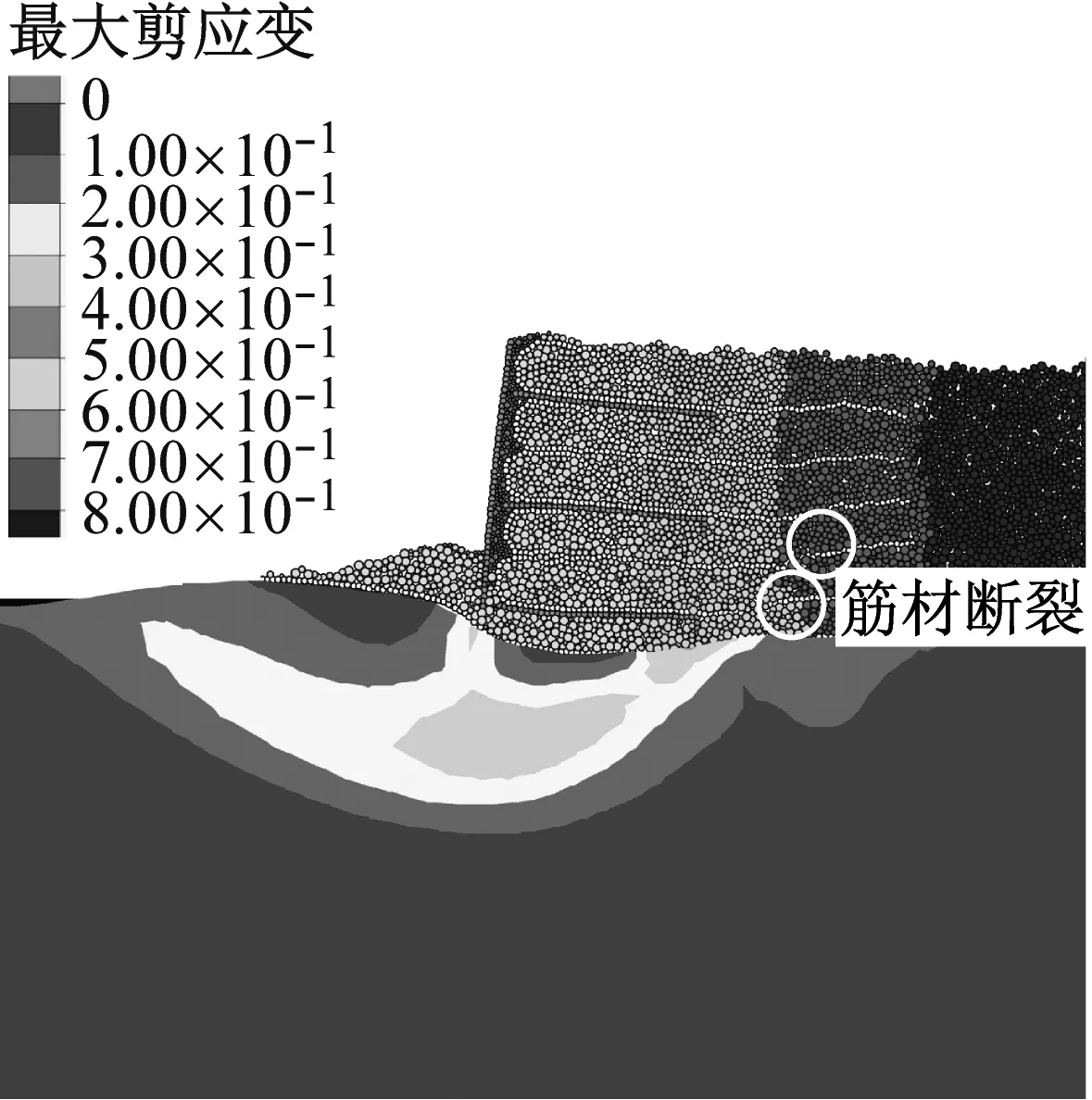
a 5 000计算步

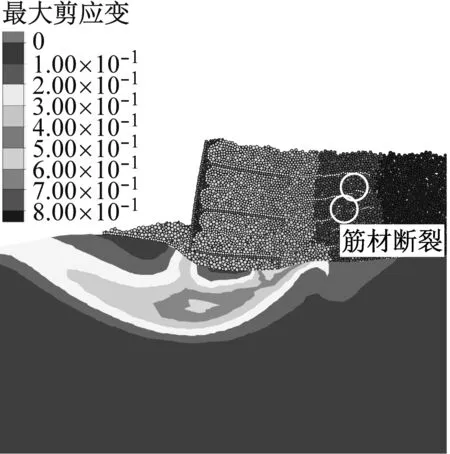
b 10 000计算步

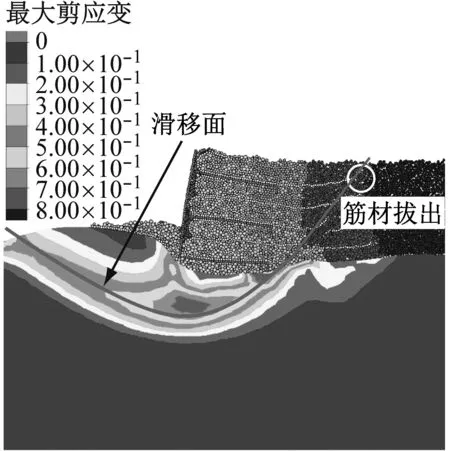
c 40 000计算步图13 软土地基上挡墙内部破坏演化过程 Fig.13 Internal failure evolution of reinforced wall on soft foundation

挡墙及地基的总位移云图如图14所示，挡墙内部破坏面与水平面的夹角也为59°，表明软土地基上刚/柔性组合加筋土挡墙内部破坏面为过底层连接件后缘的朗肯破坏面，其与地基中的圆弧滑移面一起组成挡墙复合破坏面.

图14 模型内部破坏时的总位移等值线云图 Fig.14 Displacement contour of the model in internal failure

5 结论

基于软土地基直立刚/柔性组合墙面加筋土挡墙离心模型试验，建立离散-连续耦合数值模型，采用离散单元颗粒流程序PFC和有限差分程序FLAC分别模拟加筋土挡墙和软土地基，研究软土地基直立刚/柔性组合墙面加筋土挡墙性状，并进一步探讨挡墙的内、外部稳定性，得出以下主要结论：

(1) 数值模拟的挡墙墙顶沉降、墙底地基表面沉降和墙面水平位移与离心模型试验实测结果吻合很好，两者均显示挡墙在自重及上覆荷载作用下产生显著的沉降和不均匀沉降，但挡墙整体仍保持稳定，表明该型挡墙具有很好的适应软土地基大变形的能力.

(2) 连接件埋置范围内的墙体整体刚度较大，挡墙自重及上覆荷载作用使得在刚度突变的连接件末端位置产生了明显的应力集中，同时导致此处的地基表面沉降最大.

(3) 上覆荷载作用下，刚性墙面在墙中处弯矩最大，为外侧受拉，而在墙顶与墙底处的弯矩较小，为内侧受拉；由于连接件的侧向约束作用，刚性墙面的弯矩在连接件埋置位置处发生突变.

(4) 由于软土地基刚/柔性组合墙面加筋土挡墙的加筋土整体刚度大于软土地基，变形时整体性好，使得挡墙不易产生过加筋体内部的破坏面.因此，该挡墙的稳定性一般表现为深层滑移外部稳定性，其破坏面是由过挡墙底层筋材后缘填土中的朗肯破坏面和过地基中的圆弧滑移面组成.

(5) 软土地基刚/柔性组合墙面加筋土挡墙内部稳定性表现为随地基滑移破坏，挡墙内筋材由下至上依次断裂，形成过底层连接件后缘的朗肯破坏面，其与地基中圆弧滑移面贯通形成挡墙复合破坏面.