考虑作业人员疲劳度均衡的第一类装配线平衡
2019-04-02徐立云陈贻平李爱平
徐立云, 刘 琨, 陈贻平,2, 李爱平
(1. 同济大学 机械与能源工程学院, 上海 201804; 2. 上海振华重工集团(南通)传动机械有限公司, 江苏 南通 226017)
装配是产品生命周期中的重要环节,一直以来都是国内外学者研究的重点.Boysen等[1]根据是否给定生产节拍c和工作站数量m给出了简单装配线平衡问题(SALBP)的分类方法:①SALBP-1,给定c,最小化m;②SALBP-2,给定m,最小化c;③SALBP-E,c和m都待定,最小化mc;④SALBP-F,给定c和m,求可行解.
国内外学者根据设备最少、节拍最短、平衡率最高等目标对线平衡问题进行了优化.文献[2]考虑了三个冲突的目标,建立了基于目标规划的平行装配线多目标优化模型,为平行装配线的决策者提供灵活的选择.文献[3]更好地表示了工位和任务的约束,构建了一种考虑优先关系约束、任务分区约束和工位约束的多目标优化模型.文献[4]提出并以完工率节拍为评价指标建立随机作业时间条件下的第二类装配线平衡问题模型,为随机型装配线平衡问题提供一种新的解决思路.文献[5]考虑了工件装夹方式对作业元素分配的约束,个别作业元素需共用一个工位的约束,并允许并行工位存在,解决电子装配线平衡问题.
在装配线上,作业疲劳会导致作业人员协调性和灵活性降低,注意力涣散,事故率增加,同时引起工作满意度的降低,影响生产效率和产品质量.目前,学者们对作业疲劳度的研究集中在工效学领域,只有少部分学者尝试在装配线平衡时考虑平衡作业疲劳度[6].文献[7]分析了OWAS(Ovako Working Posture Analysis System)和NIOSH(National Institute for Occupational Safety and Health),提出REBA(Rapid Entire Body Assessment)方法,根据作业姿势对工人负荷进行评估.文献[8]基于仿真技术,通过人体新陈代谢能量消耗来量化评估装配作业中人体的疲劳程度.文献[9]基于活塞工艺路线及主要工序操作分析,建立作业疲劳多指标量化模型,平衡了活塞生产线的作业疲劳度.文献[10-11]在线平衡研究时采用RULA(Rapid Upper Limb Assessment)方法对作业疲劳度进行评估.文献[12]提出采用OCRA(Occupational Repetitive Action)方法评估疲劳度,进行线平衡.文献[13-14]综合使用OCRA、RULA和NIOSH评估疲劳度,并使用两种算法求解.上述提到的评价模型中,OWAS使用范围较广,但对细节评估比较局限;NIOSH能够较好评估作业姿势但通用性不好;RULA对上肢细节评估敏感,但对整体作业姿势评估有局限;OCRA方法对姿势评分时不及REBA准确.
本文基于工效学中的REBA来评价各作业姿势风险,提出工位累计疲劳度(accumulated fatigue of station, AFS)的评估分析方法,以手工工位的单品种单边装配线为研究对象,满足多种约束,构建最少工位数和最小AFS标准差的多目标优化模型;设计基于优先权重编码的多目标粒子群算法(MOPSO),得到满足约束的非劣解.采用上述方法对某装配线实例进行工艺设计和应用.
1 作业人员疲劳度评价
1.1 作业姿势风险评价方法
作业疲劳是人在劳动生产过程中,逐渐出现的不适感,是作业能力明显下降的一种状态,是劳动生理和心理的一种复杂表现,易导致生产效率下降,发生事故.作业疲劳一般分为肌肉疲劳,精神疲劳(包括智力疲劳、技术性疲劳和心理性疲劳)和生物周期疲劳.作业疲劳度即作业的疲劳程度.
REBA方法[7]是由三位人因学专家独立地对144种作业姿势的组合进行编码,考虑伴随风险和动作等级,结合负荷、联结及活动分数,最终生成REBA值(1~15分),该评估方法具有全面、快速、适用性广的优点.
REBA方法是一种能够对各类肌肉骨骼风险进行敏感评估的姿势分析系统.该方法根据人体运动平面,将人的整个身体分成几个部分分别加以编码分析;提供了一种针对静态、动态、快速变化和不稳定的姿势情况下的肌肉活动状态的打分系统;能够反映连接(作业人员的手与作业手柄的连接)在处理负荷时的重要性;有明确紧急程度指示的动作等级;具有最小化实验需求(仅用纸和笔).
由于目前企业缺乏评估作业人员精神和心理风险的手段,而且人体受力所承受的作业负荷是造成疲劳度的主要原因之一,故本文利用REBA着重研究作业姿势和负荷引起的疲劳,暂不涉及精神负荷和生物周期疲劳.
1.2 基于REBA的作业姿势风险评估
REBA将身体分为A、B组,A组包括躯干、颈部、腿部,B组包括上臂、前臂和手腕,根据评分表对各部分分别进行评分,并对某些部位根据扭转情况和弯曲角度附加调整分值.
图1为A组中躯干运动示意图,其对应的评分如表1所示.躯干竖直时,作业人员疲劳感最小.躯干屈曲、伸展的角度增大时,不舒适度和疲劳感将会增大,因此对应分值增加.另外,当躯干发生扭曲或侧向屈曲时,躯干评分增加1分.
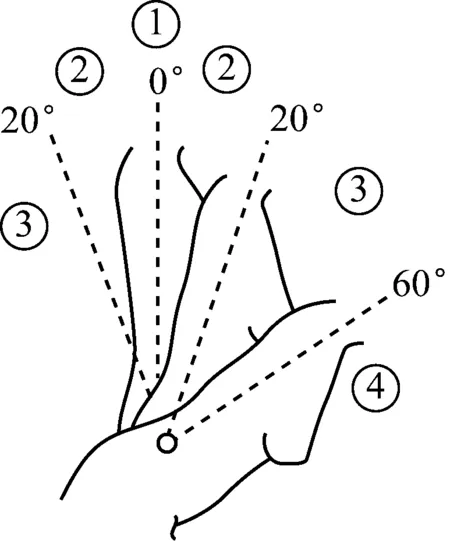
图1 躯干运动示意图 Fig.1 Motion of trunk
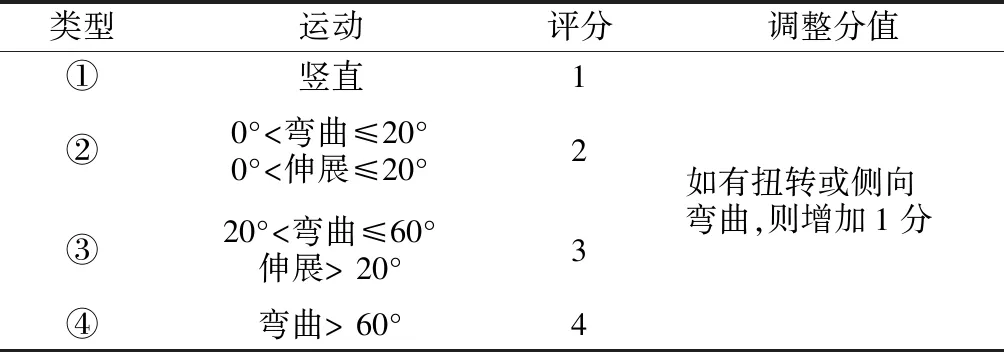
表1 躯干评分Tab.1 Score of trunk
图2为上臂姿势图,其对应的评分如表2所示.当上臂弯曲或伸展的角度增大时,评分随之增加.此外,手臂外展或耸肩时,加1分;当手臂有支撑或辅助时,减1分.
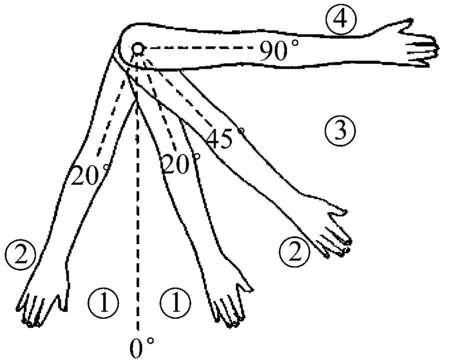
图2 上臂姿势图 Fig.2 Motion of upper arms
再对躯干、颈部和腿部(A组)进行综合评分,并根据发力和负荷情况附加调整分值;对上臂、前臂和手腕(B组)进行综合评分,并根据作业手柄握持情况附加调整分值[7].得到A组和B组综合评分后,根据表3可以得出最终REBA评分.文献[7]根据分值的高低将作业姿势的疲劳风险等级划分为5级,如表4所示.

表2 上臂评分表Tab.2 Score of upper arms
1.3 工位累计疲劳度
装配线上各工位的作业人员往往要完成多个作业,因此需要计算单个工位上作业人员的累计疲劳度,文献[15]阐述了用累计姿势风险(ARP)计算工位累计负荷的优点,采用OWAS对作业姿势打分,需对身体6个部位计算ARP及其最大值.但ARP没有考虑疲劳度随时间的累积,放大了高风险但作业时间短、减弱了低风险但作业时间长的作业元素对工位累计姿势风险的贡献.文献[16]考虑疲劳度随时间的变化,并假设为线性变化,建立了作业人员的疲劳和恢复模型.
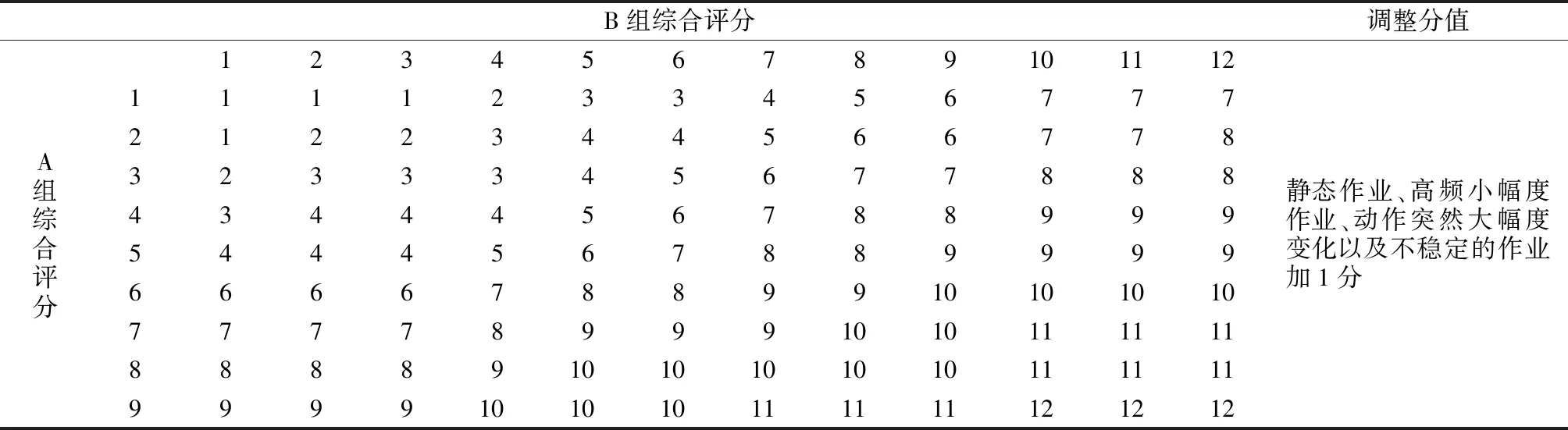
表3 REBA综合评分表Tab.3 REBA score

表4 REBA评分等级Tab.4 REBA level
本文提出同时考虑作业姿势持续时间和不同作业姿势互相影响的工位累计疲劳度(AFS).某工位有作业元素1、2和3,根据REBA得到各作业元素的姿势风险如图3所示,对应作业姿势风险为R1、R2和R3,对应作业时间为t1、t2和t3.为求单一作业姿势的疲劳度(fatigue of postures,FP),对作业姿势风险在时间上进行积分,如式(1)所示,然后根据式(2)计算AFS的值Afj.
(1)
(2)
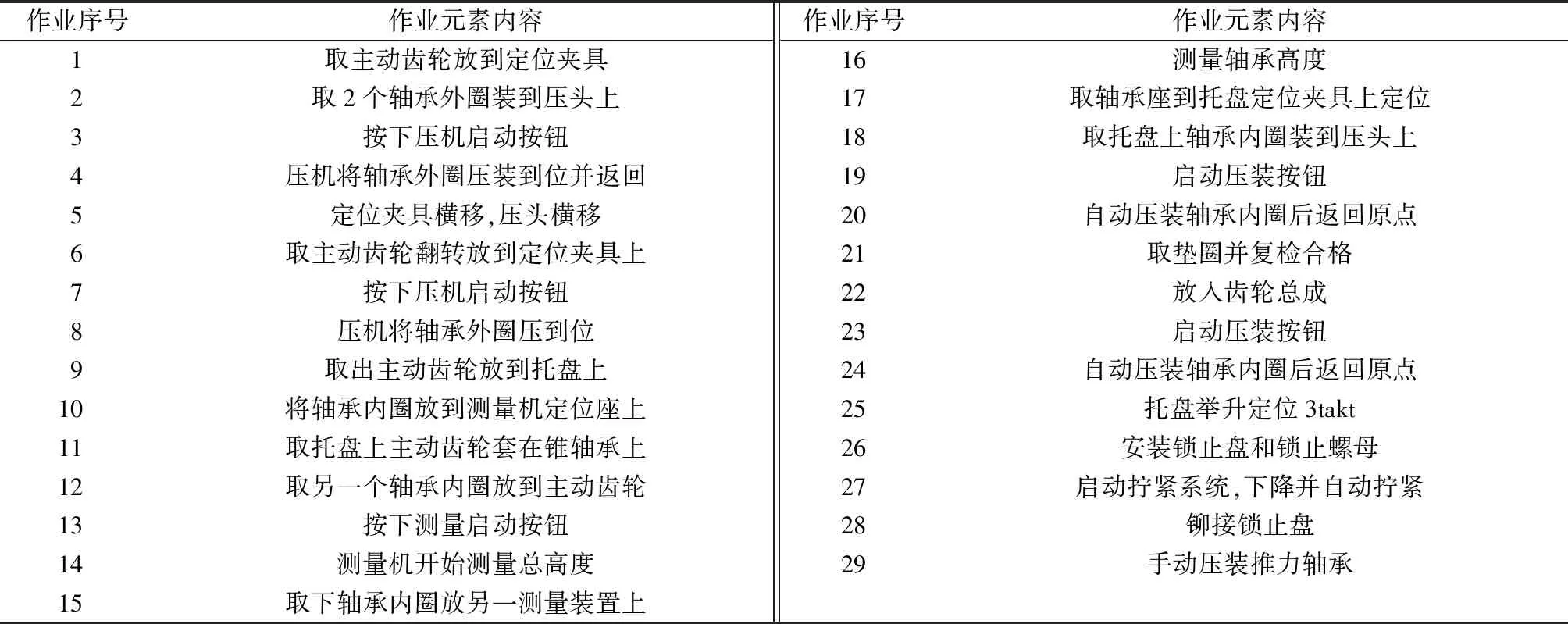
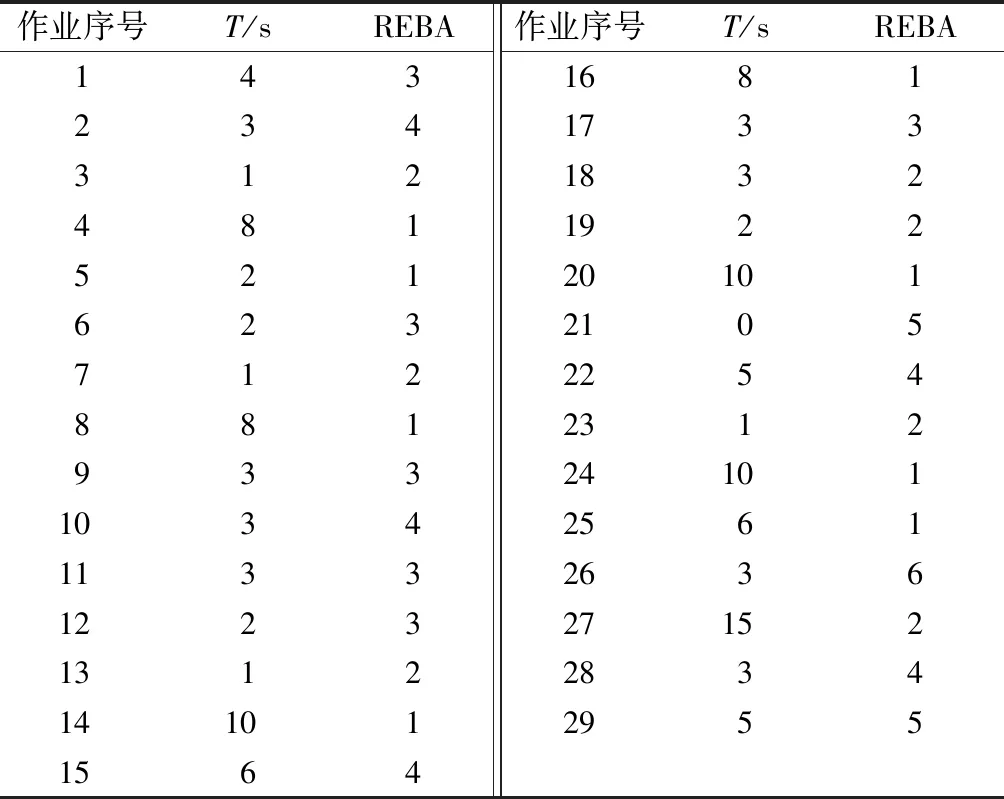
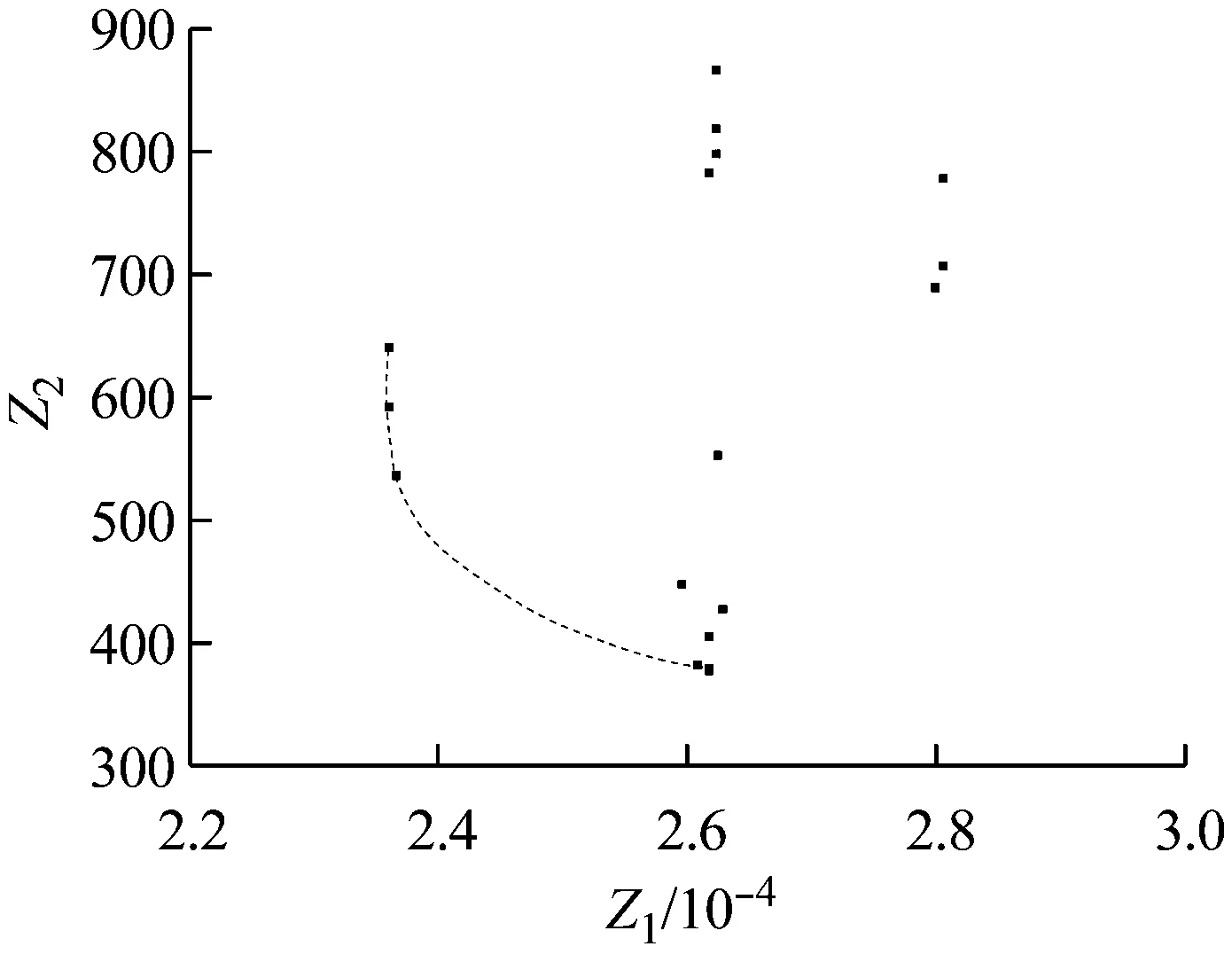
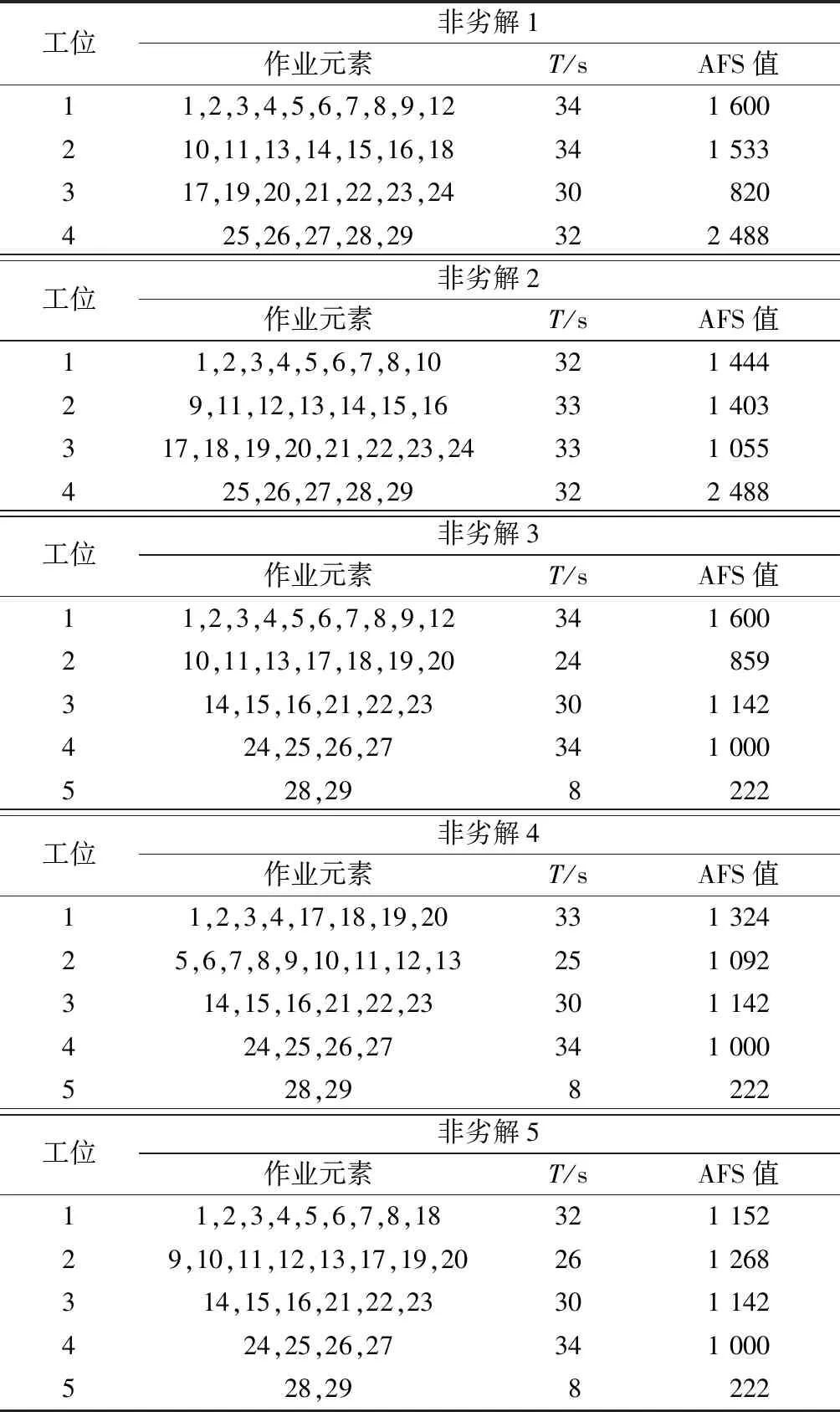
式(1)和(2)中:Fp为作业姿势的疲劳度;Ri为作业元素i的姿势风险;ti为作业元素i的时间;Tj为分配到工作站j的所有作业元素集合;(i,i′∈Tj)&(i 图3 姿势风险图 Fig.3 Risk of postures 第一类装配线平衡是给定n个作业元素及其对应时间ti,节拍为cT,在满足作业优先关系约束prec的情况下,最小化工作站数目m.其数学描述为 minm (3) 所研究的问题基于以下假设: (1) 为简化问题,论文中装配线为单一品种单边装配线. (2) 所有作业元素都必须满足优先关系约束. (3) 每个作业元素都有固定的作业时间. (4) 每台工作站的作业时间累计不能超过给定生产节拍. (5) 所有作业元素都已经是最小自然作业单位,无法进一步划分至多个工位. 本文定义以下变量: I={i|i=1,2,…,n}为作业元素集合;n为作业元素总数;j为工作站编号;m为工作站数量;STj为第j个工作站的作业时间;xij=1表示第i个作业元素被分配到第j个工作站,xij=0表示未被分配到j工作站.P=(Pa,b)n×n为装配作业优先关系矩阵,若作业元素a是作业元素b的直接优先操作,则Pa,b=1,否则Pa,b=0,a,b∈I.Q=(Qa,b)n×n为不相容作业元素关系矩阵,受工艺、设备或安全因素影响,一些作业元素不能同时分配在同一工作站,Qa,b=1表示作业元素a和b不相容,否则Qa,b=0,a,b∈I.R=(Ra,b)n×n为同工位约束矩阵,由于某些作业元素在同一装配专机上完成,因此需要分配至相同工位,Ra,b=1表示作业元素a和b有同工位约束,否则Ra,b=0,a,b∈I. 在SALBP-1中,优化目标为最小化工作站数目m.但以m作为评价函数会出现搜索过程改进缓慢、随机性高的现象.文献[17]改进了SALBP-1的目标函数,新目标函数在搜索过程中能够实现函数值的持续改进,提升算法效率,该目标函数适用条件同SALBP-1.本文为求工作站数目最小值及其倒数,因此第一个目标函数为 (4) 本文模型第二个优化目标是为了使各个工作站的作业疲劳度均衡,因此计算整线所有工作站AFS值的标准差为 (5) 因此,考虑作业人员疲劳度均衡的第一类装配线平衡模型如下: (6) 约束条件如下: ∀i (7) (8) (9) xaj+xbj≤1,(a,b)∈Q∀j (10) (11) 式(7)保证所有作业元素都被分配一次;式(8)为优先关系约束;式(9)保证各工作站作业时间不超过节拍约束;式(10)保证不相容作业元素不被分配到同一工位;式(11)保证有同工位约束的作业元素被分配到同一工位. 粒子群算法(PSO)是从鸟类的觅食行为中抽象出来的一种智能优化算法,在求解流水作业排序[18]、混流装配线排序[19]、车辆路径问题[20]时表现出较强全局优化能力和较快收敛速度.文献[21]提出的离散PSO求解线平衡问题时已经优于遗传算法.多目标优化问题的各个子目标之间往往是矛盾的.因此,本文设计MOPSO,对本模型求解Pareto最优解集,供企业决策者选择. 为了保证在解码后能够得到可行的作业序列,提高解码效率,本文采用基于优先权重的排列编码方式[21].粒子在D维度搜索空间时,其位置表示各项作业元素的优先权重大小.针对有同工位约束的作业元素,本文将其合并为一个作业元素进行处理. 本文解码过程中先得到可行序列,在满足作业元素不相容约束下将作业元素放入工作站.解码完成时,所有作业元素也分配完毕,使得操作分配至尽量少的工位,加快算法对第一个目标函数的改进速度.具体解码算法步骤如下: 步骤1,选取入度为0(没有前驱,直接优先作业元素)且优先权重最大的作业元素,如有多个符合条件的作业元素则从中随机选取一个. 步骤2,判断当前工作站添加该作业元素后是否超过节拍,判断该工作站是否有作业元素与待分配作业元素同工位不相容,如果未超过节拍且无不相容作业元素则放入该作业元素,并转步骤4,否则转步骤3. 步骤3,选下一个工作站作为当前工作站,转步骤2. 步骤4,更新作业元素分配矩阵,更新工作站时间,更新优先关系矩阵(删除已分配的操作). 步骤5,判断所有作业元素是否被分配完毕,否则转步骤1. 每个粒子对应一个D维向量,代表潜在解,根据目标函数可以计算每个粒子的适应度函数值.根据本文的数学模型,适应度函数如下: F1=minZ1 (12) F2=minZ2 (13) MOPSO对多个目标同时优化,引入非劣解概念,即在可行域中存在一个问题解,若不存在另一个可行解,使得一个解中的目标全部优于该解,则该解成为多目标优化问题的非劣解.初始筛选非劣解集时,将初始化的粒子中的非支配解(即不存在其他粒子的所有适应度值都优于该粒子)放入非劣解集,并在粒子更新前从中随机选择一个作业群体最优粒子.更新非劣解集是把不受非劣解集中粒子支配的新粒子放入,每次更新前仍从中随机选择一个例子作为群里最优粒子.在更新个体最优粒子时,选择新粒子和个体最优粒子中的支配粒子,如果都不是支配粒子,则从中随机选择. 粒子按式(14)和式(15)通过个体极值和群里极值更新自身的速度和位置,式(14)右边第一部分表示上一次搜索速度的惯性,第二部为粒子自我学习,第三部分是粒子间相互学习. (14) (15) 算法求解流程如下: 步骤1,初始化粒子位置. 步骤2,根据3.1的步骤进行解码,满足式(7)~(11)的约束. 步骤3,计算各粒子适应度值,F1根据式(4)和(12)计算,F2根据式(2)、(5)和(13)计算. 步骤4,更新个体和群体最优粒子. 步骤5,根据粒子支配关系筛选支配解,更新非劣解集. 步骤6,粒子速度和位置更新(包含变异). 步骤7,达到最大迭代次数,算法结束,输出非劣解集;否则返回步骤2. 变速箱是用来实现汽车发动机输出转速和汽车车轮的实际输出行进速度的变速传递装置.某企业自动变速箱装配工艺包括制动器分装、轴承座分装、差速器分装、中间轴分装、离合器及输入轴分装、前壳体总装.整线生产纲领设计节拍cT=34 s,需设计最少工位数的装配线,属于第一类线平衡问题.本文以轴承座分装线为例,该分装线需要安装轴承座、锥轴承、中间轴主动齿轮、垫片、锁止盘、锁止螺母和推力轴承.在合并具有同工位约束的作业元素后,共有29个装配作业元素,作业元素14,16和4,5,8,20,24不能在同一工位.各作业元素如表5所示,作业优先关系如图4所示. 图4 作业优先关系图 Fig.4 Graph of precedence REBA所示评分过程:作业元素1如图5所示,操作者取主动齿轮放到定位夹具.作业人员躯干前倾角度在20°~60°之间,无扭转,根据REBA的躯干评分表得到躯干评分为3分;颈部俯视角度在0°~20°之间,有扭转,评分为2分;作业人员无负荷走动,腿部评分为1分;大臂抬起角度在20°~45°之间,无附加分,大臂评分为2分;小臂活动角度在60°~100°之间,小臂评分为1分;手腕活动角度小于15°,有转动,评分为2分.在A组综合评分中,作业人员负载小于5 kg,无附加分,故A组总分为3分;B组综合评分中,作业人员操作手柄完美适配,故B组总分为2分.最后由表3可知作业元素1的综合REBA评分为3分.对其余作业元素依次进行REBA评分,各作业元素时间及REBA评分如表6所示. 表5 轴承座分装线作业元素内容Tab.5 Tasks of bearing seat line 图5 作业元素1示意图 Fig.5 Task 1 表6 各作业元素时间及REBA评分Tab.6 Work time and REBA score of tasks Win10 64位操作系统、4GB内存和Intel(R) Core(TM) i5-5200 CPU(2.2GHZ)环境下,在MATLAB 2013a中编写多目标粒子群算法.用MOPSO算法对式(3)~(13)的模型进行计算,其中式(5)中的AFS由式(2)计算所得.算法中各参数设置如下:种群规模为100,最大迭代次数为200,非劣解集规模为100,惯性权重ω=0.5,学习因子c1=1,c2=2,粒子坐标为29维的向量,每个坐标为(0,100)的随机数.算法运行时间为157.306 s,运行效率较高,得出的非劣解分布如图6所示.图6中横坐标为第一个优化目标适应度函数值,即各工位作业时间平方和倒数;纵坐标为第二个优化目标适应度函数值,即所有工作站AFS值的标准差;其中5个非劣解分布在虚线上.算法搜索取得较好效果,非劣解数量可以保证决策效率. 图6 非劣解分布图 Fig.6 Distribution of non-inferior solutions 从表7、8可以看出,非劣解1和2的工位数为4,非劣解3、4和5的工位数为5.和非劣解2相比,非劣解1中AFS的标准差较大,其工位3的AFS明显低于其他工位,但具有容纳新作业元素的能力;非劣解2中各工位作业时间较平均,且整体AFS较非劣解1更平衡.非劣解3、4和5相比,各工位的作业时间变化不大,但非劣解5的各工位AFS值的标准差最小,作业人员疲劳度较其余两解最为平衡.非劣解2和5相比,非劣解2工位数少,AFS的标准差小于非劣解5.尽管非劣解5的AFS标准差较小,但只有前4个工位的疲劳度得到很好的均衡,工位5的AFS值较极端,这是由于该分装线工位较少,作业元素增加时此现象会改善. 表7 非劣解适应度值Tab.7 Fitness value of non-inferior solutions 表8 非劣解作业元素分配情况Tab.8 Tasks distribution of non-inferior solutions 因此,考虑到新增工作站的成本以及作业人员的疲劳度均衡,非劣解2是较优的选择,可以减小作业人员的心理不平衡度,肌肉骨骼损伤以及事故发生率.算例结果显示,随着F2函数值的改进,各工位累计疲劳度将得到进一步平衡,验证了所提方法的有效性. 本文针对第一类线平衡问题,考虑作业人员疲劳度的均衡,装配提出工位累计疲劳度的分析方法;同时考虑了作业元素的优先关系约束、作业元素同工位不相容约束和同工位约束,建立了多目标装配线平衡数学模型;设计基于优先权重编码的MOPSO,采用粒子解码后得到可行操作分配方案;并通过实际案例对单边装配线进行分析和验证.本文所提方法能够快速准确地对作业疲劳度进行评估,为该类生产线平衡问题提供了新思路.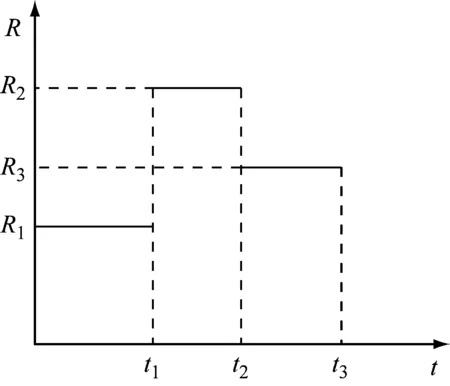
2 考虑作业人员疲劳度均衡的第一类装配线平衡建模
2.1 问题描述及相关假设
2.2 变量及数学模型
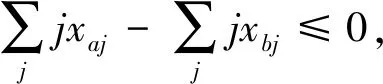
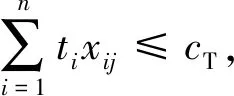
3 多目标粒子群算法描述
3.1 粒子的编码与解码
3.2 适应度函数
3.3 粒子的更新
3.4 算法流程
4 实际案例



5 结语
