利用带流向阀门拓扑模型评价供水管网可靠性

曾 文， 汪鼎雄， 陈金娅

(1. 中国地质大学(武汉)信息工程学院， 湖北 武汉 430074； 2. 顺丰科技有限公司武汉分公司， 湖北 武汉 430200)

供水管网是城市的基础设施，由水源、管段和水力控制元素(水泵、阀门、贮水池等)组成，以合适的水流压力向用户供水[1].供水管网可靠性是指供水管网在规定的条件下和规定的时间内保量、保压、保质完成供水功能的能力.可靠性是评价供水管网性能的重要指标，广泛应用于管网优化和设计[2].

管网可靠性分为水力可靠性和拓扑可靠性[3].水力可靠性是指供水管网在特定时间段内满足用户流量和压力需求的可能性[4].水力可靠性计算一般使用模拟法[5-6]，通过水力模型计算来评价供水需求的满足程度.拓扑可靠性是指供水管网系统满足用户终端与水源点间路径连通的可能性[7].

拓扑可靠性计算一般使用解析法，面向管网的拓扑结构来分析发生故障时管网的连通性及从水源点到取水点的可达性.Wager等[8]运用可达性和连通性评价供水管网系统的可靠性，其中可达性是指某个需求节点至少连接一个水源节点的可能性，连通性是指所有节点都至少连通一个水源节点的可能性.吴小刚等[9]基于管网的节点-连边拓扑模型生成割集，运用最小割集法对管网结构进行风险评价.Yazdani等[10]从复杂网络的角度，提出了崩溃临界值、代数连通度和谱隙3个指标用于评价供水管网的鲁棒性.陈芃等[11]使用拓扑分析计算管网发生事故时需要关闭的阀门与影响区域，用以量化供水管网的性能.Walski[12]提出单元-阀门图(segment-valve diagram，SV)模型，运用图论方法来分析阀门的数量和位置是否满足管网可靠性需求.

本文改进拓扑可靠性研究中的单元-阀门图模型，提出一种新的供水管网模型——考虑流向的单元-阀门图(segment-valve diagram with flow directions，SV-FD)模型，刻画阀门对不同方向水流的阻断作用，然后基于该模型设计供水管网更为精细的拓扑可靠性评价指标，并应用于3个城市的供水管网，验证新指标的价值.

1 SV图模型与可靠性评价

阀门是保障管网可靠性的关键因素，其分布显著影响管道事故的影响范围和处理效率，几乎所有管道事故的处置都要通过关闭若干阀门来形成隔离停水区域.Walski[12]指出传统图论中的节点-连边图(node-edge graph，NE 图)难以表达发生事故时需要关闭的阀门，对于可靠性分析有着一定的局限性，因此提出一种新的阀门拓扑(valve topology)网络模型，即单元-阀门图(segment-valve diagram，SV)模型.

SV模型以关断单元(segment)的定义为基础.设图G(V,E)为代表某个供水管网的原始节点-连边图(NE)模型，则图G的关断单元是满足如下条件的极大导出子图：子图中任意两个节点之间至少存在一条不以阀门为内部节点的路径.该供水管网的单元-阀门图G′(V′,E′)是以图G的全部关断单元为顶点，以关断单元边界的阀门为边构成的原始图G的伪对偶图.Jun等[13]使用节点-弧段关联矩阵和阀门附属位置矩阵(node-arc incidence and valve location matrices)求解segment-valve图.曾文等[14]给出了基于GIS的节点-连边网络模型求解SV图，以及通过该图进行关阀搜索的算法.

作为例子，图1a给出一个供水管网的节点-连边图模型.该模型可转化成包含7个关断单元的SV图，如图1b所示.与NE图相比，SV图更加简洁，能更清晰地体现阀门在管网中的关断作用.

Walski将SV图作为管网可靠性分析的工具，把关断单元边界处阀门的平均数量和关断单元内部管段的平均数量作为表征管网可靠性的指标.Jun等[13]进一步提出一系列指标评价管网可靠性.其中核心指标可描述如下：

(1) 关断单元平均管长规模LS为

LS=LT/NS

式中：NS为关断单元总数；LT为管网中管段总长.

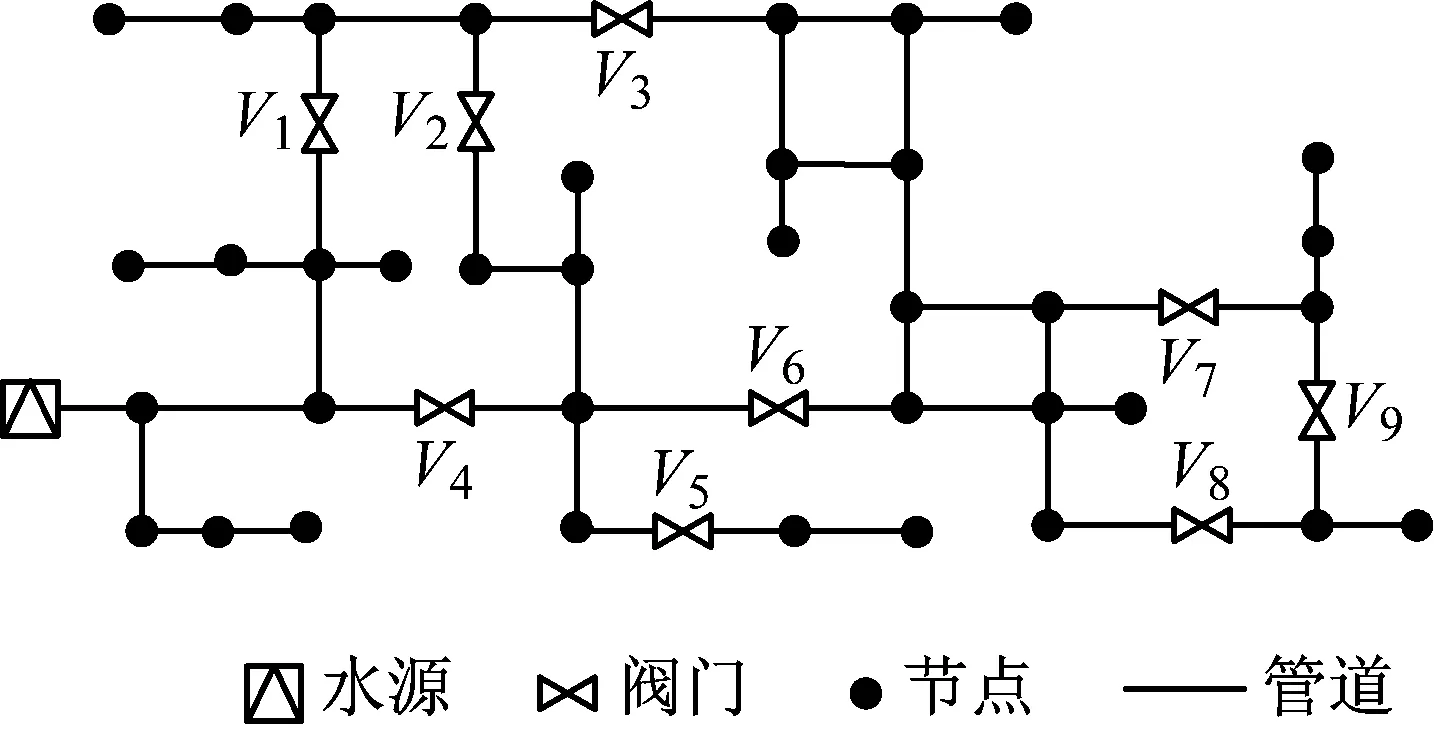
a NE图模型

b SV图模型 图1 节点连边图及其对应的单元阀门图模型Fig.1 Node-edge graph and its corresponding segment-valve diagram

若关断单元i内管段总长为LS i，则

(2) 关断单元平均管段规模PS为

式中：PS i是第i个关断单元包含的管段数.

(3) 阀门相对于管长的密度(单位长度管段包含的阀门数)VSL为

VSL=NV/LT

式中：NV为管网中阀门总数.

(4) 阀门相对于管段的密度(每管段包含阀门数)VSP为

VSP=NV/NP

式中：NP为管段总数.

(5) 关断单元平均边界阀门数VB为

关断单元规模用来表征爆管造成的停水范围，规模越大表示事故影响越大；阀门密度代表控制事故范围的能力，密度越大，故障越容易限制在局部范围；管段单元边界阀门数量与应急抢修时间密切相关，该值越小，事故越容易在短时间内得到控制.

尽管有上述经典评价指标，Jun 等[13]注意到SV图用于可靠性分析仍有缺陷：发生爆管的关断单元常常并不代表完整的停水区域，下游的管网也会因为与水源的隔离而停水，使用关断单元自身的规模及边界阀门数量来评价管网可靠性并不准确.以图1b为例，设水源在关断单元u1内，若关断单元u5内出现爆管，则u6和u7因为位于下游，也会停水，而且维修时通常只需要关闭上游阀门V3和V6,下游阀门V7和V8并不需要关闭.虽然爆管点下游管网在失压状况下可能发生水流反向，但下游蓄积水量毕竟有限，现场处置时倒流已经发生并持续一段时间，所以一般不需要关闭下游阀门.

可见，SV图没有考虑水源与各个关断单元的连通关系，将关断单元边界的全部阀门等同对待，对阀门阻断来水作用的描述不够细致，故而基于SV的可靠性评价指标仍有不足.

2 SVFD模型

为了精细描述阀门对水流的实际阻断作用，体现爆管事故对管网的真实影响，本文在SV图基础上发展形成一种新的模型——考虑流向的单元-阀门图(segment-valve diagram with flow directions，SV-FD)模型.SV-FD模型是基于SV图改进的有向图，与原始SV图具有相同节点集合，每个节点代表一个关断单元，其中包含水源的关断单元被专门标记，称为水源单元.SV-FD的弧段集合则按照以下原则形成：节点ui和uj间存在有向边，当且仅当：①ui和uj间有公共阀门Vk；② 原始SV图中存在从水源单元经关断单元ui及阀门Vk到达关断单元uj，并且不以uj为中间节点的路径.

通过以上描述可知，SV图每个连接关断单元ui和uj的阀门Vk，在SV-FD有1条或2条有向边与其对应.如果有向边存在，当关断单元uj内发生爆管时，阀门Vk处将存在从ui到uj的水流，为了阻止水流进入uj，需要关闭阀门Vk.反过来，如果有向边存在,则在ui中出现爆管时，需要关闭阀门Vk以阻止水流进入ui.这样，SV图中一个阀门在考虑可能的水流方向时，在SV-FD中转变为1条有向边或2条反向的有向边.可以把每条有向边看作1个只阻挡固定方向水流的阀门，称为单向阀门.

在教学实践中，教师常用任务教学法突破重难点帮助学生掌握某知识点，然而在真实工作过程中，完成一项工作是需要一个系统的知识任务网。基于工作过程，项目化教学是以工作过程为导向，以岗位任务为核心，引导学生逐一完成由多个相互关联的任务组成的项目来捕获系统知识，形成自身知识链或知识网，从而在此过程中体验知识价值。目前在中职旅游专业课程如《模拟导游》《导游业务》中进行项目化教学初步实践。

将SV图G转化为SV-FD模型G′的过程如下：

(1) 将SV图G中包含水源的关断单元标记为水源单元，将全部边转化为两条方向相反的弧，形成有向图G1.

(2) 求解SV的全部割点[15]，然后针对每个割点a，检验删除割点后形成的各个连通分量，若连通分量c不包含水源，则由c中节点指向a的所有弧段都代表不可能流向，从G1中删除该有向边.

(3) 从G1中按照步骤(2)删除所有符合条件的有向边，即得到SV-FD模型G′.

图2是在图1所示SV图基础上形成的SV-FD模型，其中灰色填充节点u1表示水源单元.可以看到原始SV 图转化为有向图SV-FD后，多数阀门都对应于两条有向边(即两个单向阀门)，表示该阀门在两端的关断单元发生爆管时，都需要关断以阻断水流.但是有些阀门，如V5，只对应于一条有向边(即一个单向阀门),反向有向边已经被删除.当u4中发生爆管时，水流可由u1经u3到达u4，只有关闭V5才能阻止水流.但是当u3中发生爆管时，只需要关闭以u3为终点的阀门，即V2、V4和V6，由于无水流从u4流向u3，所以不需要关闭阀门V5.将上述需要关闭的3个阀门称为关断单元u3的关键阀门.

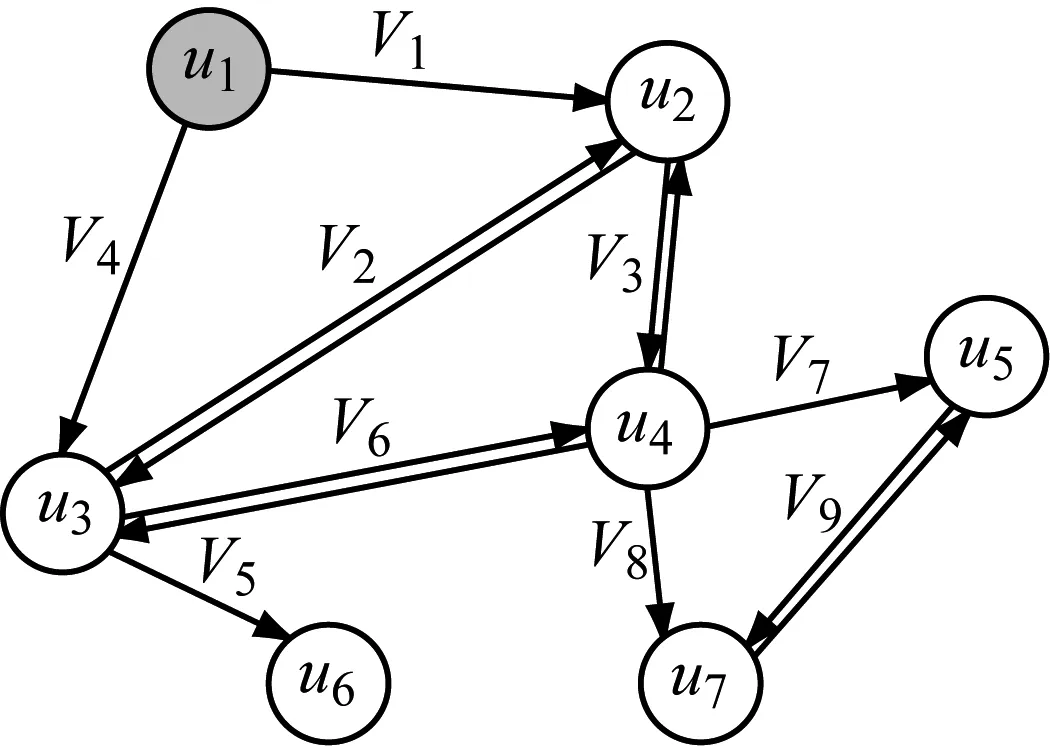
图2 SVFD模型实例 Fig.2 A sample of SV-FD model

不仅如此，沿着单向边向下游搜索，将得到更多停水区域，即u4.将u3和u4称为u3内爆管的实际停水区域.可见，相较于SV模型，SV-FD能够更精细地刻画阀门对水流的阻止作用，弥补了前者在关键阀门识别以及停水范围确定方面的不足.使用SV-FD模型更有利于对管网可靠性的精确评价.

3 基于SVFD的可靠性评价

本文采用单向阀门、关键阀门和实际停水区域的概念，改进前述5个经典评价指标，面向事故影响、隔离难度和抢修时间，提出基于SV-FD的5个新指标，用于供水管网的拓扑可靠性评价.

(1) 关断单元平均事故影响管长LC为

式中：NS为关断单元总数;LCi为关断单元i内爆管实际停水区域的管段总长.

(2) 关断单元平均事故影响管段数PC为

式中：PCi为关断单元i内爆管实际停水区域的管段数量.

(3) 单向阀门相对于管长的密度(单位长度管段包含的单向阀门数)VFSL为

VFSL=NVF/LT

式中：NVF为单向阀门总数.

(4) 单向阀门相对于管段的密度(每管段包含单向阀门数)VFSP为

VFSP=NVF/NP

式中：NP为管段总数.

(5) 关断单元平均关键阀门数VC为

式中：VCi为第i个关断单元的关键阀门数.

4 可靠性评价实例

本文选用中国3个城市的口径300 mm以上实际供水主干管网作为研究对象(记为GW1、GW2和GW3)，对比分析基于SV的经典可靠性评价指标和本文提出的基于SV-FD的改进指标的评价结果.3个城市的NE图(部分)如图3所示.GW1所在城市位于江苏省，地形平坦，管网分布均匀，整体呈网格状分布；GW2与GW1的空间分布面积相近，但所在城市位于广西省，多山地和丘陵，城市分布受地形限制，管网分布不均匀，呈放射状，局部呈块状分区分布，环状管网主要分布在各分区内部；GW3是江苏省某市供水管网，空间分布面积明显大于前两者，在主城区密集，多呈网格状，环状管网较多，周边新城区向市郊延伸了许多管径较大的干管，这些干管同时连接成较大的环.

3个管网基于NE图生成的SV-FD模型如图4所示.为了清晰展示，图中用一条双向边表示两条方向相反的有向边.

3个管网原始NE图及相应SV图的基本信息如表1所示.表中割点占比是SV图中割点占顶点的比例，可以表达管网拓扑的成环程度，数值越小，管网连通性越强.

首先使用基于SV图的5个经典评价指标进行可靠性评价.结果如表2所示.

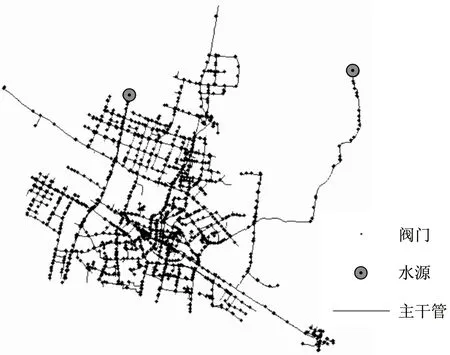
a GW1

b GW2(部分)

c GW3(部分) 图3 管网的NE图 Fig.3 Node-edge graphs of WDNs

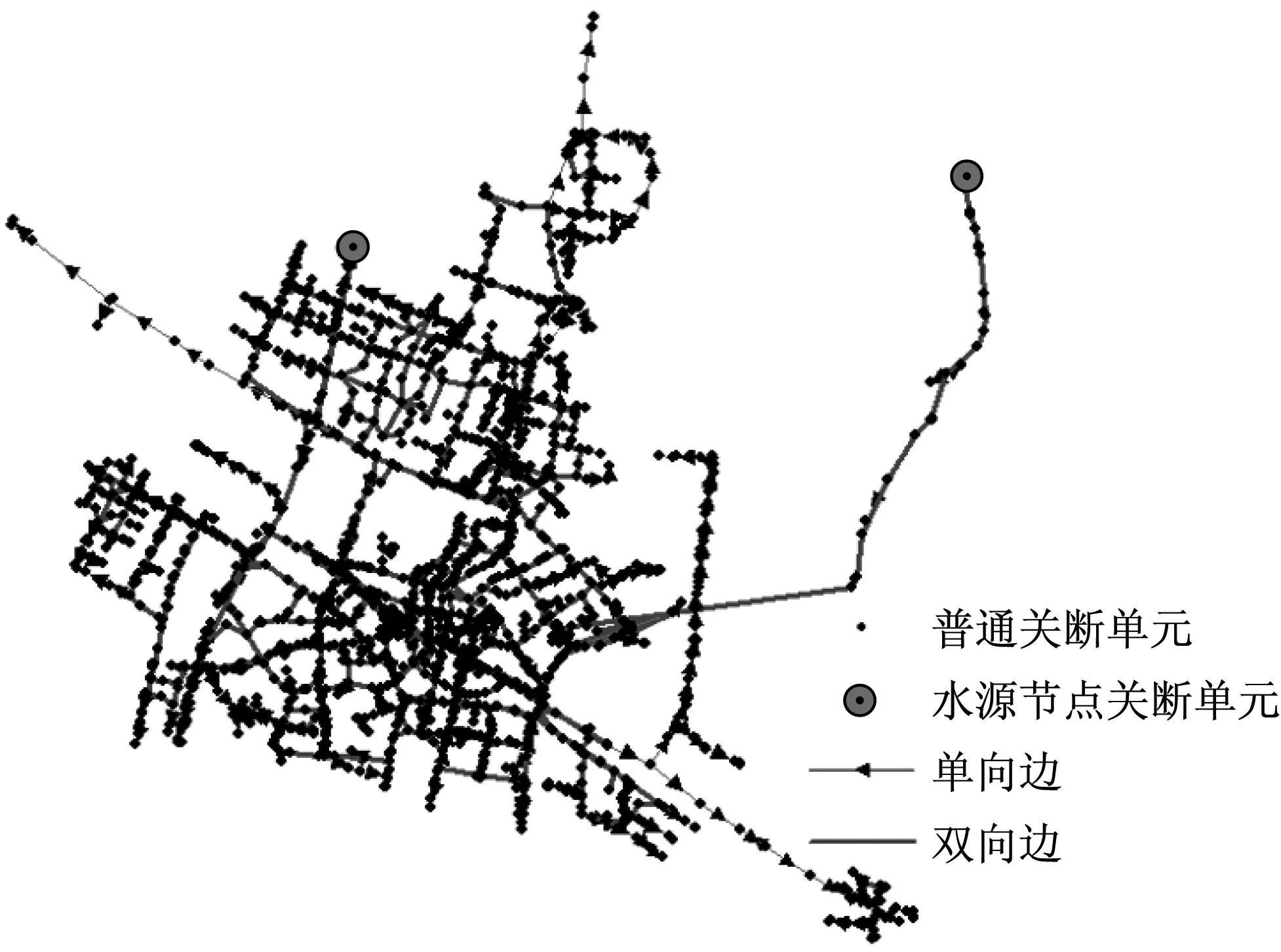
a GW1

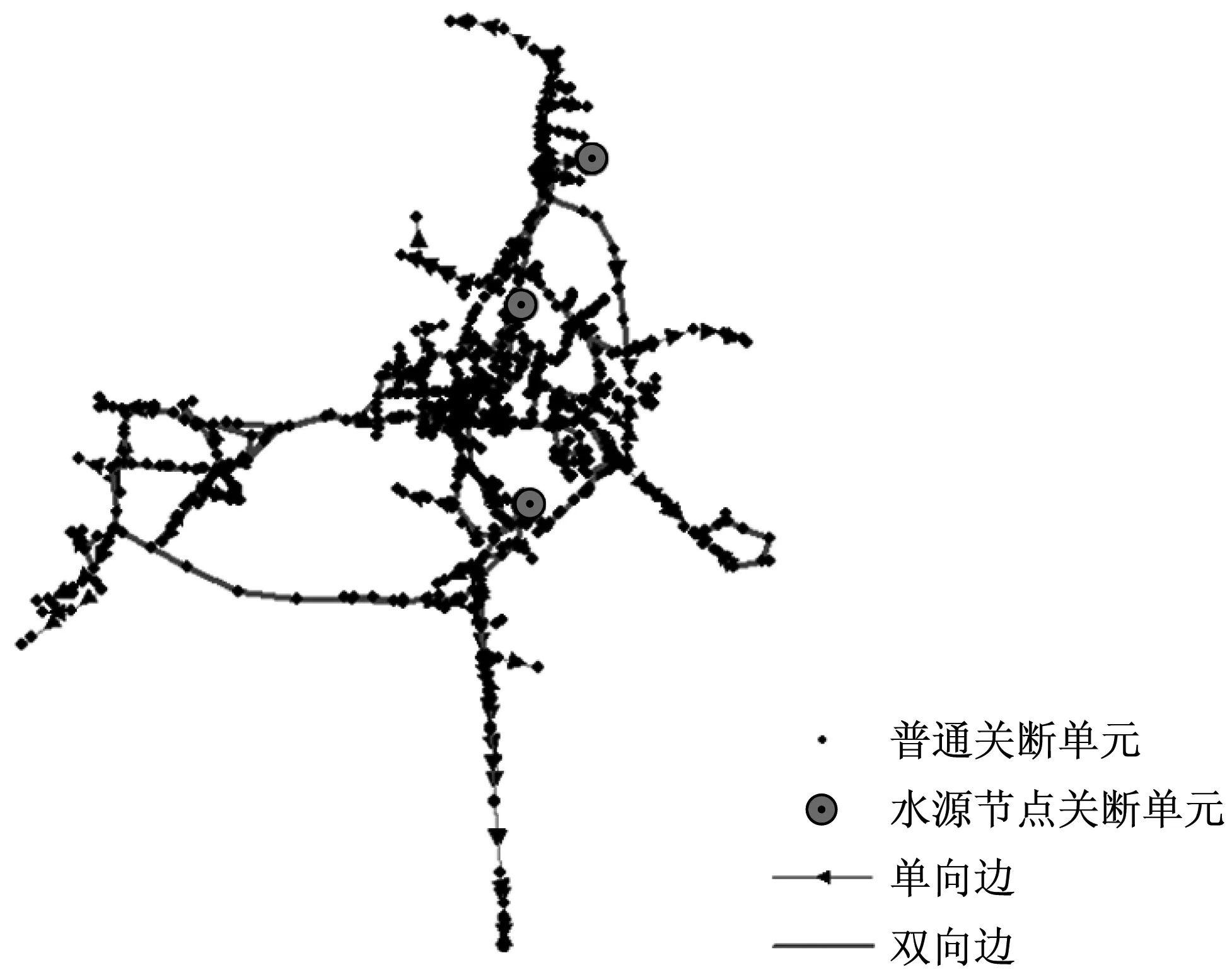
b GW2(部分)

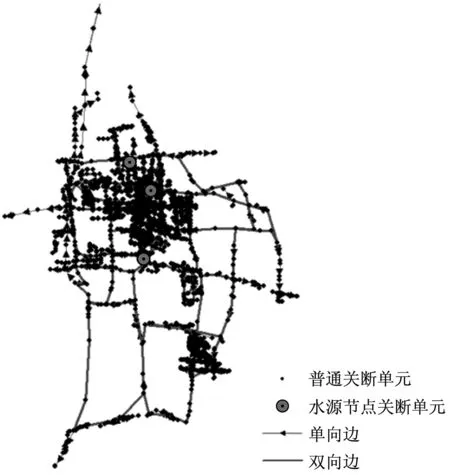
c GW3(部分) 图4 管网的SVFD模型 Fig.4 SV-FD models of WDNs

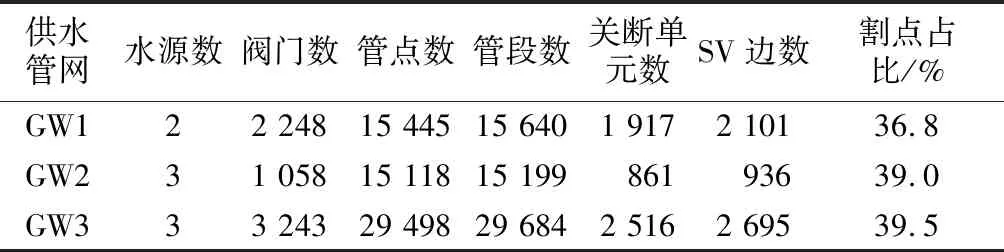
表1 3个管网实例的总体信息Tab.1 General information of 3 WDNs

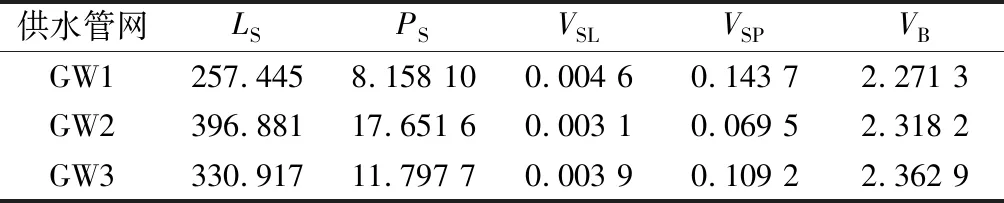
表2 3个管网基于SV模型的可靠性评价指标值Tab.2 Reliability evaluation indices of 3 WDNs based on SV model

从表2中LS、PS指标可以看到，关断单元规模为GW1GW3>GW2，显示GW1最容易将事故控制在局部范围，GW2则最不容易完成局部化控制.指标VB表示事故时需关闭阀门数，有GW1

使用基于SV-FD模型的5个新指标评价3个管网的可靠性，结果如表3所示.

表3 3个管网基于SVFD模型的可靠性评价指标值Tab.3 Reliability evaluation indices of 3 WDNs based on SV-FD model

从表3可见，平均事故影响管段数PC的排序为GW1

表3中单向阀门密度指标VFSL、VFSP，与表2中SV模型下阀门密度指标VSL、VSP的排序一致，即GW1>GW3>GW2.但是VFSL、VFSP指标间的差异更大，区分度更好.

SV-FD模型下关断单元平均关键阀门数VC呈现GW1>GW2>GW3的排序，与表2中平均边界阀门数VB的排序 GW1

从表3的5个指标值可以看到，管网GW1阀门密集，事故影响范围小，但应急关阀时间较长.管网GW2、GW3阀门较稀疏，事故影响范围大，但应急关阀时间较短.从事故后果看，GW1可靠性最高；从应急时间看，GW3的可靠性最高.

分析不同管网评价指标值的差异，可以找出影响管网可靠性的关键因素，采取有针对性的措施来提高可靠性.对于GW2、GW3，由于管网分布不均匀，成环程度低，支段多，导致事故影响范围大，即LC、PC指标大.欲降低这两个指标，应增加管网成环程度，降低割点占比，同时增加阀门密度，提高VFSL、VFSP指标值，减小关断单元规模.GW1管网分布均匀，成环程度高，阀门密集，关断单元规模小，但是关键阀门数量多，事故应急时间长，应该对阀门布局进行优化.

5 结论

本文基于供水管网阀门拓扑模型SV图，提出一种改进的管网模型——SV-FD，标记了阀门处的水流方向，可以更加精准地判定爆管时需要关闭的阀门，得到真实完整的停水区域.基于该模型设计了5个评价指标，从事故影响、隔离难度和应急时间等角度量化评价管网拓扑可靠性.运用这些指标分析了中国3个城市的供水干管，发现与基于SV图的传统经典指标相比较，改进指标能够更准确更清晰地反映管网事故的实际影响和处置难度.利用SV-FD模型评价供水管网可靠性，可以发现阀门布局和成环程度方面存在的问题，对管网的规划设计和优化改造具有重要参考价值.