不同形式节理的岩质边坡失稳演化离散元分析

蒋明镜， 江华利， 廖优斌， 刘 笋， 王华宁

( 1. 同济大学 土木工程防灾国家重点实验室， 上海 200092；2. 同济大学 岩土及地下工程教育部重点实验室， 上海 200092；3. 上海理工大学 环境与建筑学院， 上海 200093； 4. 河海大学 土木与交通学院， 江苏 南京 210098；5. 同济大学 航空航天与力学学院， 上海 200092)

西部大开发战略大力推动了西部地区交通、水利水电枢纽等建设的快速发展.西部地区多高山峡谷地貌，存在众多构造特殊、地质条件复杂的高陡边坡，其中发育的节理等不连续结构面构成了岩体软弱结构面，严重影响边坡稳定性，直接影响道路路堑和隧道洞室开挖等的施工及运营安全，一直以来备受岩土工程界关注[1].岩质边坡按节理等软弱面倾向和坡面倾向的关系可分为顺层岩质边坡和反倾岩质边坡.已有学者分别对这两种形式的边坡失稳问题做了相关研究.在顺层岩质边坡方面，刘小丽等[2]根据弹性板的稳定理论,利用能量法对缓倾角顺层岩质边坡的弯曲失稳机理进行了探讨；陈从新等[3]根据相似理论开展了地质力学模型试验，通过试验对比说明了顺层岩质边坡的主要变形方式为滑动变形；李祥龙等[4]利用离心机试验研究了顺层岩质边坡的动力稳定性和破坏机制，发现其破坏受结构面控制.在反倾岩质边坡方面，左保成等[5]通过室内物理力学模型试验研究了层厚、倾角等对反倾岩质边坡稳定性的影响，指出反倾岩质边坡的变形破坏模式为倾倒变形折断破坏；苏立海等[6]利用数值分析研究了反倾岩质边坡的破坏模式及机理.虽然对顺层边坡或反倾边坡的破坏研究取得了一些成果，但需进一步在对等条件下对二者进行宏微观不同层面的对比分析，以深入了解顺层和反倾岩质边坡的不同失稳特性及机制，对不同节理形式边坡的设计及加固等工程有重要的指导意义.

边坡失稳分析常用方法有极限平衡法、物理模型试验和数值模拟方法.极限平衡法根据力和力矩平衡计算边坡安全系数，因计算简便在工程实践中被广泛应用，但其岩体为刚体的假设，不能很好反映岩体内部结构面对边坡稳定性的影响.物理模型试验可在一定程度上模拟工程现场，但试验条件严格且价格昂贵，对复杂边坡失稳机理的系统研究缺乏实用性.数值模拟方法为非连续破坏演化过程的深入研究提供了广阔的平台，如Cundall等[7]提出的离散单元法(DEM)以牛顿第二定律为理论依据，各块体或颗粒根据受力状态运动，可相互分离独立运动，能反映岩块间的接触、分离和倾倒等大位移问题，适用于节理岩质边坡的稳定性分析.如Nishimura等[8]利用离散元商业软件PFC2D模拟分析了完全均质岩质边坡的滑动机理；Jiang等[9]提出一种新的微观接触模型并利用离散元法分析了两组节理岩质边坡的破坏机理；杨忠平等[10]在边坡振动台试验的基础上采用UDEC软件分析了边坡在反复微震下变形和稳定性变化规律.

本文采用离散元方法，分别建立了顺层和反倾岩质边坡计算模型，利用重力增加法模拟了这两种形式边坡的失稳演化过程.从边坡形态、胶结破坏分布、滑体运动等方面对比分析顺层和反倾岩质边坡的失稳特征和机理，以期为不同形式节理边坡工程的设计和加固等提供有价值的参考.

1 模型介绍及参数选取

离散元模拟中，选取合理的微观接触模型能让模拟结果更准确地反映岩石材料的力学性质，使模拟过程事半功倍.本文采用考虑胶结尺寸的微观接触模型[11]，已有模拟[12]表明该模型能很好地模拟岩石的宏观力学特性.该微观接触模型力学响应分法向、切向和抗转动向三部分，如图1所示.

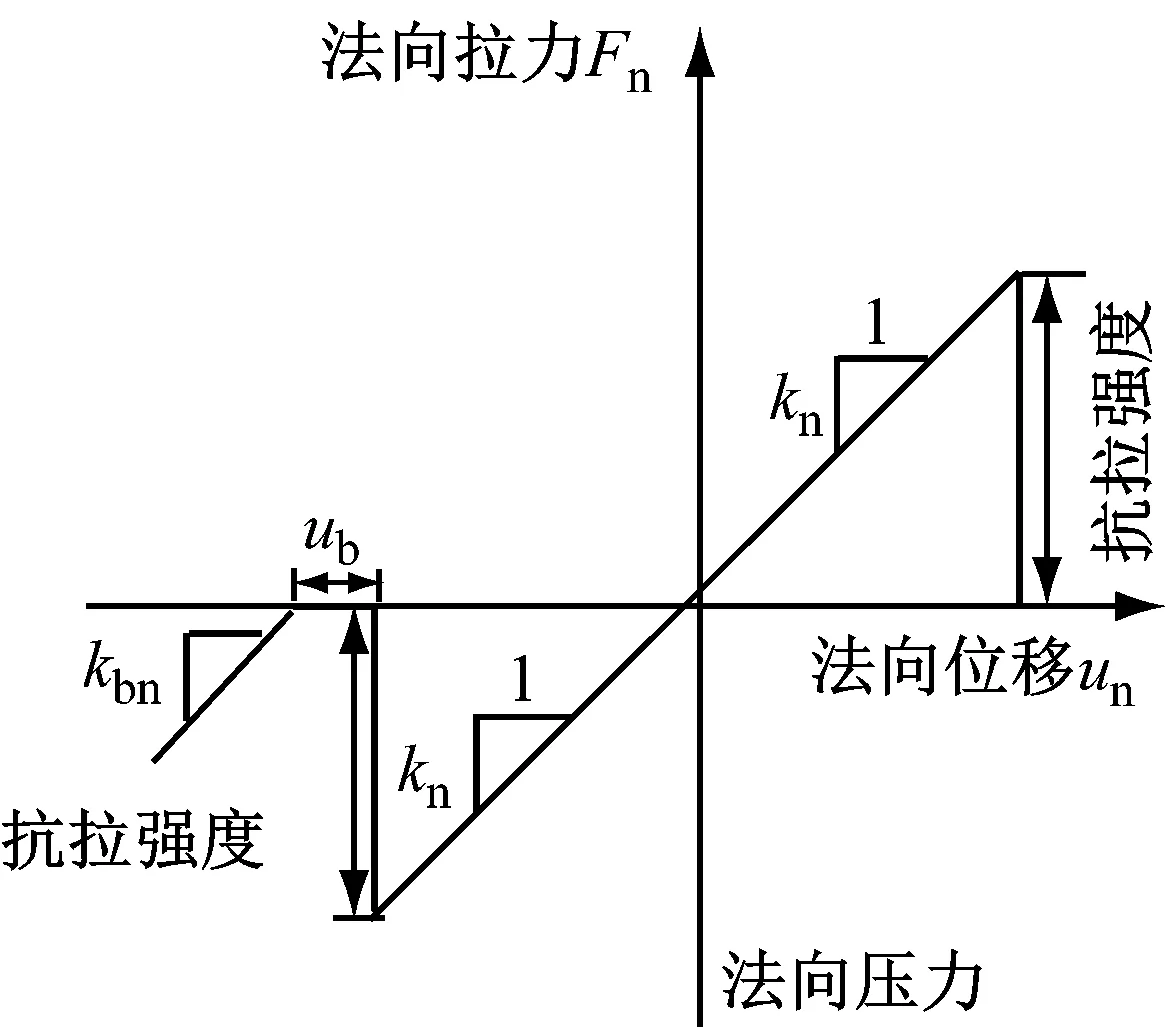
a 法向

b 切向

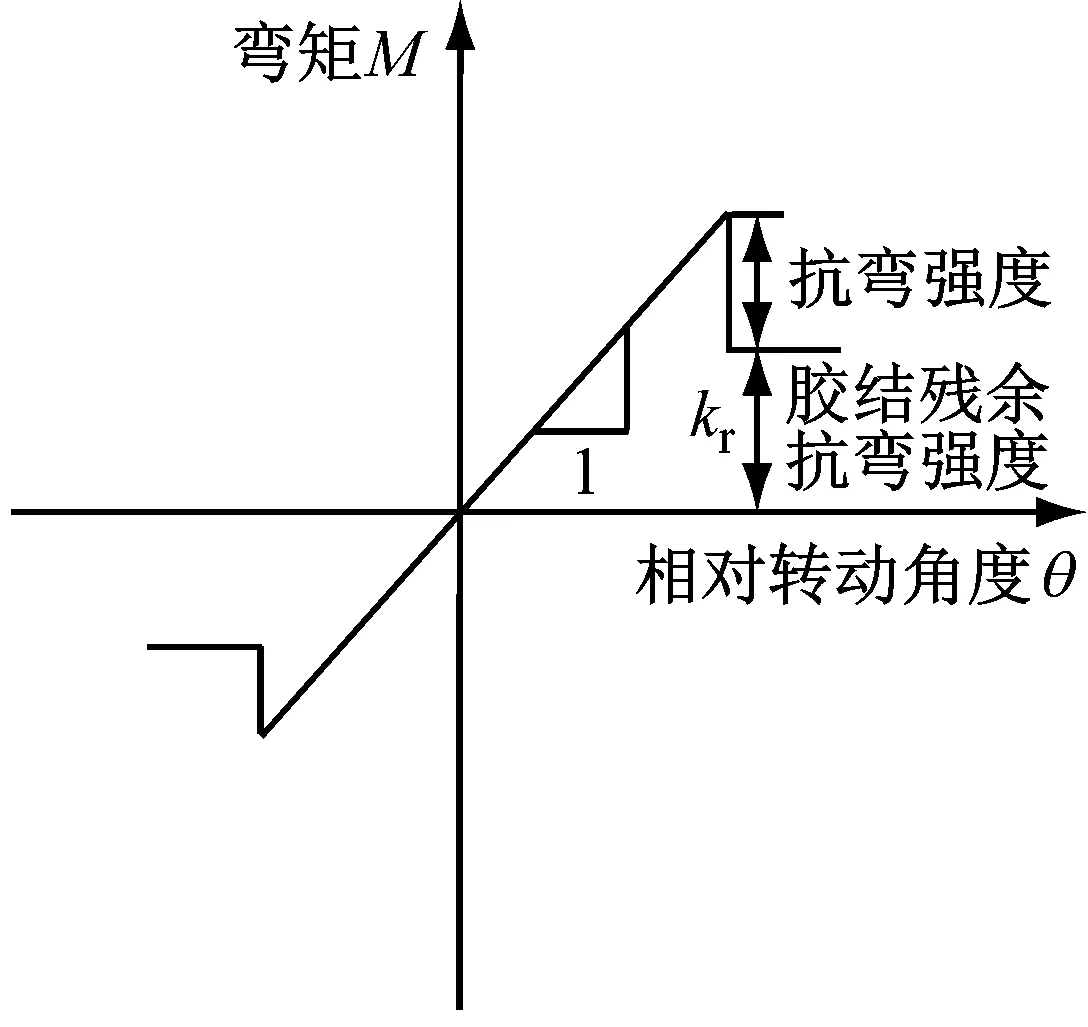
c 转动向 图1 接触模型力学响应[13] Fig.1 Mechanical response of contact model[13]

图1中，ub为胶结厚度;kn、ks、kr分别为接触法向、切向和转动刚度;kbn为颗粒法向刚度.胶结破坏前，法向、切向和转动向荷载全部由胶结承担，即kn、ks、kr为胶结法向、切向和转动向刚度.胶结破坏后，法向受力为拉伸时强度为零，受力为压缩时荷载由颗粒承担；切向抗剪强度为胶结残余强度；转动向抗转动能力为胶结残余抗弯强度.基于PFC2D 5.0自带的微观接触模型，将该模型的力学响应和强度准则通过C++编写成动态链接库文件(.dll文件)，并放入软件的安装目录中，在PFC2D 5.0的命令行中输入调用命令即可调用该模型.

本文模拟的岩石是一种软弱的沉积岩——灰屑岩(calcarenite)，广泛分布于我国西部.其单轴抗压强度σc为2.15 MPa，巴西劈裂试验强度σt为0.34 MPa，弹性模量E为0.29 GPa[14]，黏聚力c为0.60 MPa，内摩擦角φ为29.0°[15].制备DEM岩石试样时采用和陈贺[16]一致的级配，该级配由15种粒径组成，最大粒径为2.0 mm，最小粒径为0.5 mm，平均粒径为1.3 mm，级配曲线的不均匀系数和曲率系数分别为2.4和1.1，能较好地模拟岩石材料力学特性.通过模拟室内试验，得到微观参数与宏观力学指标的关系，根据目标力学指标反推微观参数.模拟单轴压缩试验，改变颗粒刚度得到弹性模量与颗粒刚度间的关系，根据目标弹性模量插值得到微观颗粒刚度参数；采用同样的思路，分别改变胶结抗拉、抗压强度，模拟单轴压缩试验和巴西劈裂试验确定微观胶结强度参数；改变胶结弹性模量，模拟得到与黏聚力的关系，确定胶结弹性模量；模拟双轴压缩试验，分别得到内摩擦角和颗粒摩擦系数、抗转动系数及胶结弹性模量的关系，得到对应的微观参数.最终确定模型微观参数如表1所示.其对应宏观参数与灰屑岩的力学参数对比如表2所示，相对误差绝对值均控制在10%内.

表1 模型微观参数Tab.1 Micro parameters of the model

表2 岩石试样宏观力学参数Tab.2 Macro mechanical parameters of rock sample

2 边坡数值计算模型

运用DEM数值模拟软件PFC2D 5.0建立边坡计算模型过程如下：

(1)制备岩石试样.在满足边界条件下，选取尽可能少的颗粒数，通过分层欠压法[17]生成含30万个颗粒、目标孔隙比为0.2的均匀岩石样本，并施加胶结模型.

(2)切削成坡.删除颗粒，形成坡角为75°、60°和45°的模型边坡.

(3)重力固结.利用离心机试验原理，将切削后的边坡在200g(g=9.8 m·s-2)的加速度下进行固结，边坡尺寸放大了200倍，对应原型边坡高74 m.75°坡角边坡的详细尺寸见图2.

(4)生成节理.实际岩质边坡节理分布复杂，本文将其分布简化为平行均布节理，如图2所示.节理参数如表3所示(节理连通率为k=(l1+l2+…+ln)L-1,式中各参数如图2b节理部分所示).由于节理内摩擦角与岩石相近、黏聚力可忽略不计，故生成节理时可用去胶结法(bond removal method)[18]将节理范围内颗粒胶结强度参数设为零而其他参数和岩体参数一致.最终形成岩质边坡模型如图2所示.

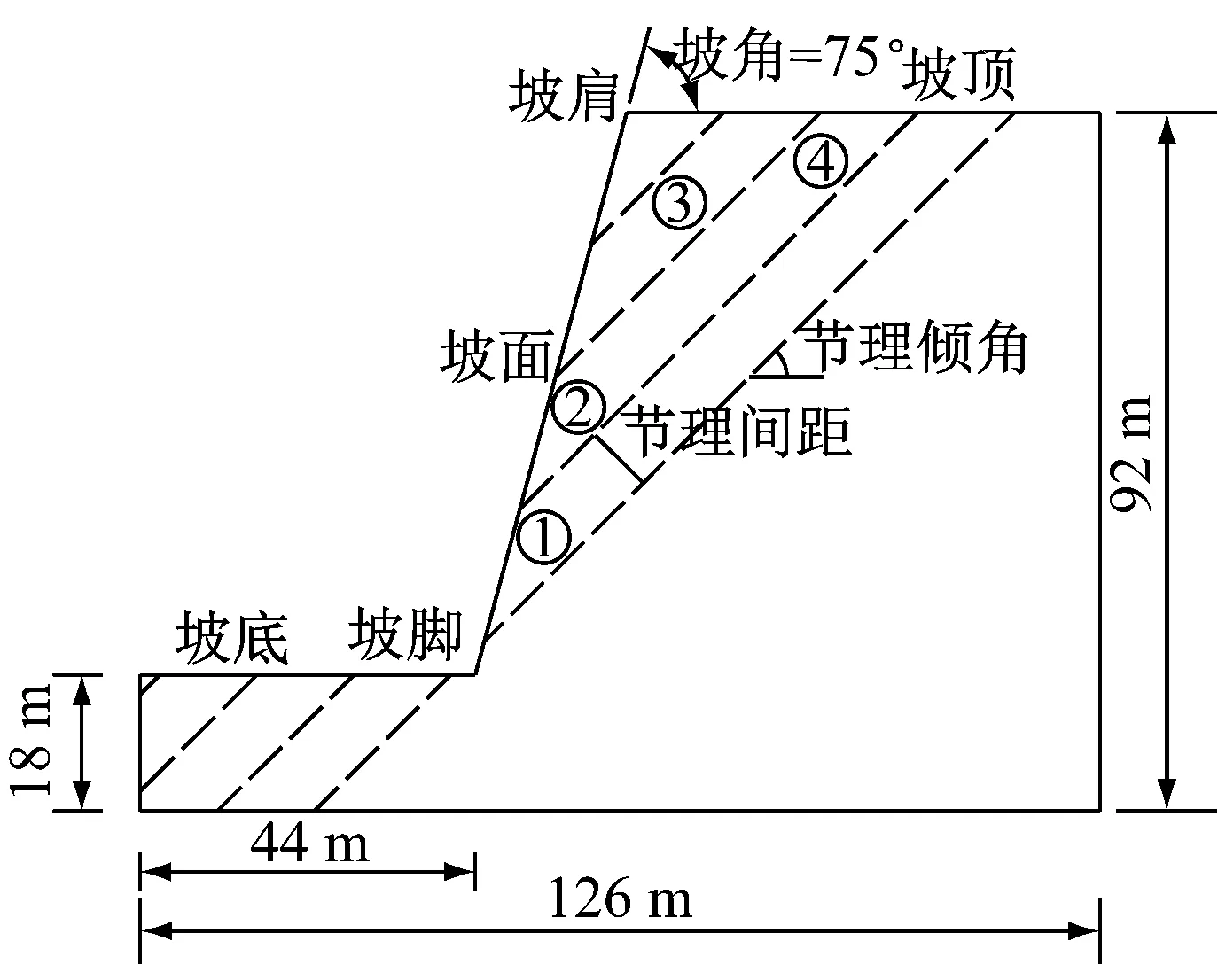
a 顺层岩质边坡

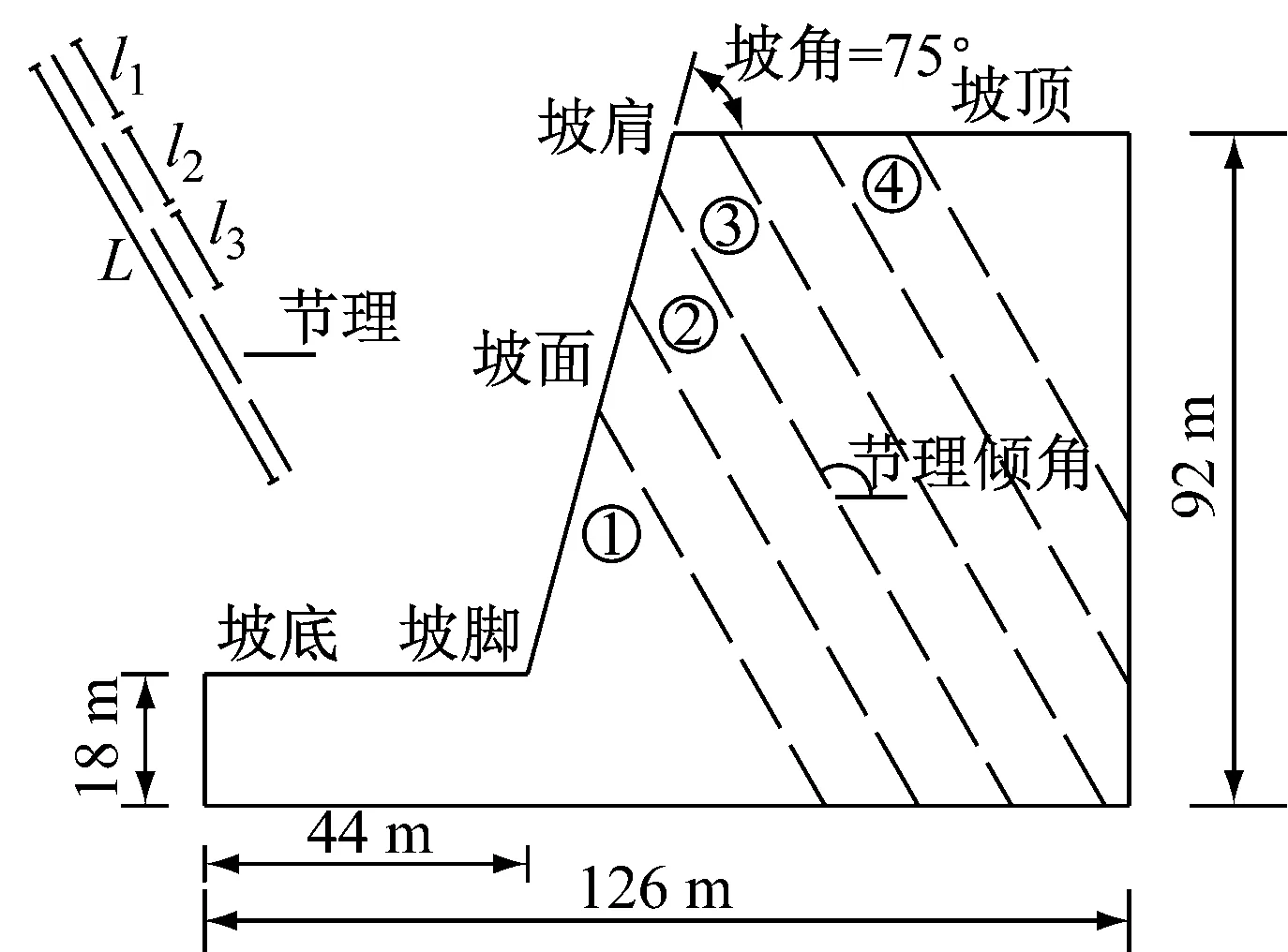
b 反倾岩质边坡 图2 边坡原位模型 Fig.2 In-situ models of slopes

表3 节理参数Tab.3 Parameters of joints

3 模拟结果及分析

利用离散单元法模拟边坡失稳过程时，通常采用强度折减法或重力增加法.已有的研究表明[13,19]，利用这两种方法研究边坡失稳过程时，可得到相近的结果.本文采用重力增加法模拟分析边坡的破坏过程.重力增加法的基本思想是不断增加边坡所受重力[20]，使边坡内胶结破坏形成微裂隙，在重力较小时，边坡胶结破坏数目保持稳定，裂纹不再发展，边坡处于稳定状态；重力场增大到一定值时，边坡胶结破坏数目持续增大，裂纹迅速发展，可认为边坡在该重力场下发生破坏.

3.1 边坡破坏过程

边坡的失稳破坏过程可根据边坡的形态及滑体运动状态分为三个阶段：起滑阶段、破坏阶段和渐趋稳定阶段.模拟过程中在坡脚处设置了刚性墙拓展颗粒运动空间，以模拟完整的边坡破坏过程，同时兼顾计算效率.图3和图4分别为各阶段顺层和反倾岩质边坡的颗粒分布图和胶结破坏分布图.边坡的颗粒分布图反映边坡在各阶段的宏观整体形态，胶结破坏分布图反映边坡的破坏位置.

a 起滑阶段的颗粒分布

b 破坏阶段的颗粒分布

c 渐趋稳定阶段的颗粒分布

d 起滑阶段的胶结破坏分布

e 破坏阶段的胶结破坏分布

f 渐趋稳定阶段的胶结破坏分布 图3 顺层岩质边坡破坏过程 Fig.3 Failure process of bedding slope

a 起滑阶段的颗粒分布

b 破坏阶段的颗粒分布

c 渐趋稳定阶段的颗粒分布

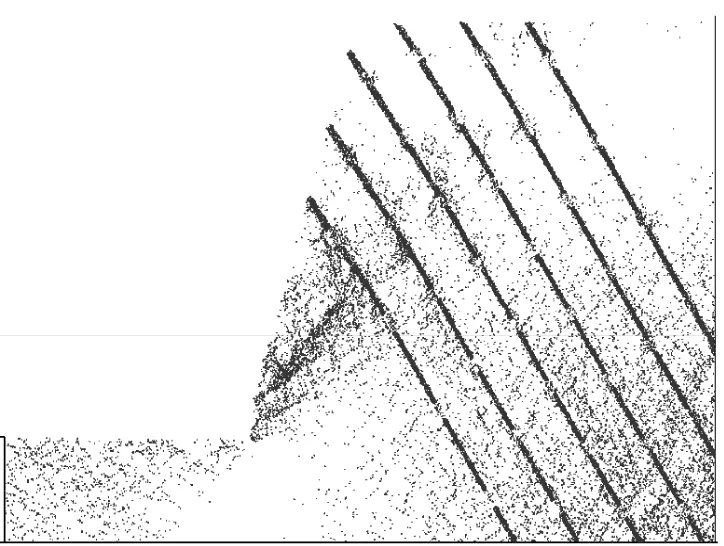
d 起滑阶段的胶结破坏分布

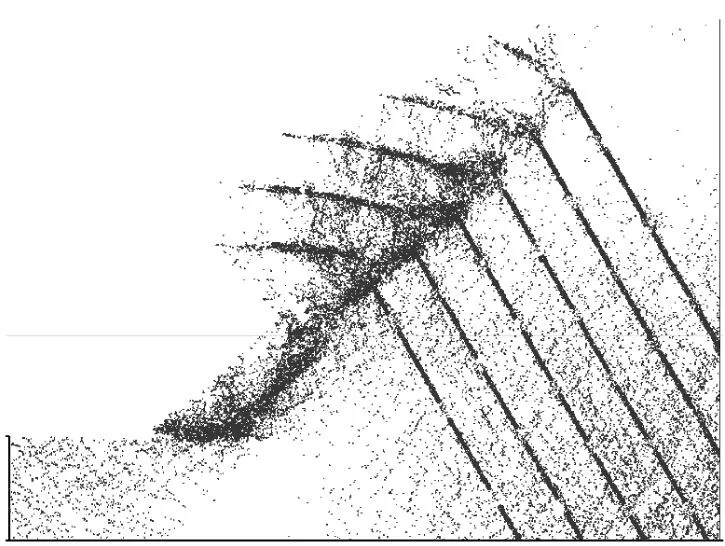
e 破坏阶段的胶结破坏分布

f 渐趋稳定阶段的胶结破坏分布 图4 反倾岩质边坡破坏过程 Fig.4 Failure process of toppling slope

(1)起滑阶段：起滑阶段岩体内裂隙开始发育、扩展和延伸，但未发生岩块滑动.由图3a和图4a可观察到，坡脚处最早出现裂隙，并有向上发展的趋势.图3d和4d中，胶结破坏点集中在坡脚附近和岩桥所在位置，岩桥出现贯通.结合颗粒分布图和对应的胶结破坏分布图可观察到，顺层节理边坡表现为共面节理贯通，形成滑裂面；反倾节理边坡表现为近坡面区域发生共面节理贯通，分割岩体形成条状岩块，不同节理面间出现裂纹，向非共面节理贯通的趋势发展，切割条状岩块，形成滑裂面.

(2)破坏阶段：此阶段裂隙贯通，切割岩体形成滑动体，边坡形态严重改变，滑动体剧烈运动.顺层节理边坡中，上部岩块沿贯通的节理面发生整体滑动，脱离母体，大块滑坡体逐渐分离成多个小滑块，胶结破坏集中在节理和滑动体内.反倾节理边坡中，坡脚处岩块沿滑裂面向下滑动，非共面节理完全贯通，将上部切割成的条状岩块，条状岩块受重力作用以各自的左下角为支点翻转向下运动，互相碰撞破碎，胶结破坏集中于节理和破碎岩块.

(3)渐趋稳定阶段：边坡剧烈破坏完成后，各岩块的位移速度逐渐减慢，变形逐渐停止，岩块在坡脚不远处堆积，最后完全稳定下来.从颗粒分布图可以看出，顺层节理边坡滑体主要集中在坡脚附近，滑动距离较小，反倾边坡破碎体滑出坡脚一定距离，破碎体沿水平方向均匀分布，无块体集中现象.

3.2 滑坡体运动信息

模拟过程中在边坡不同位置布置了测量圆，测量圆位置如图2所示，记录各区域的速度大小和位移路径如图5和图6所示.

a 顺层岩质边坡

b 反倾岩质边坡 图5 边坡不同区域速度 Fig.5 Velocity of different areas of the slope

由图5a可以观察到，顺层节理岩质边坡区域①和区域②先有速度，随后区域③、④产生速度，即坡脚附近为薄弱区，先产生滑动，随后上部岩块失稳起滑，边坡加固时应先考虑处理坡脚附近区域.当边坡进入滑动破坏阶段后，区域③、④较区域①、②先出现速度的陡升，滑坡体与边坡母体相互碰撞引起了较大的速度波动，同时滑坡体内岩块破碎分离，导致各个区域的速度开始出现较大差异.区域②和区域③的峰值速度最大，两者基本相等，区域①的峰值速度最小.从图6a可以看出，区域①和区域②的水平位移差距很大，说明坡脚处的岩块发生了严重的破碎分离.区域④的竖向位移比区域③小，而且水平位移也很短，说明区域④的岩块堆积在了坡脚附近.综合对比各个区域的位移路径，基本可以推断，边坡滑动停止后，滑坡体的前缘和后缘部分，堆积在坡脚附近，如区域①和区域④；滑坡体的中部沿着坡底产生了较远距离滑动，如区域②和区域③，应进行锚固处理.

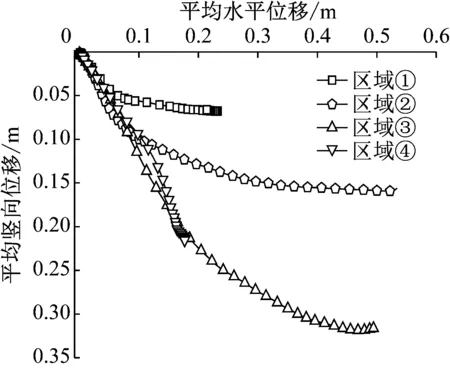
a 顺层岩质边坡

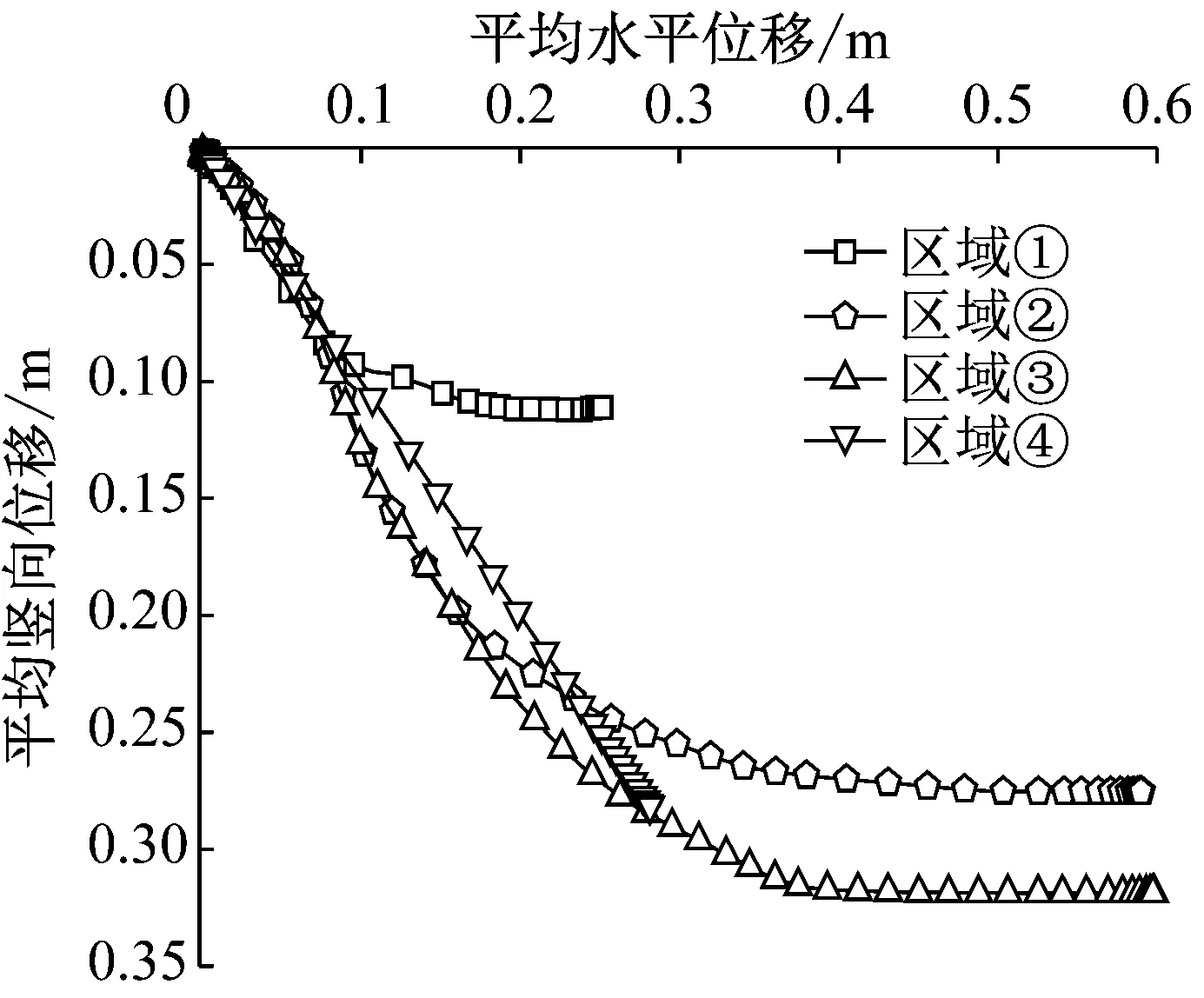
b 反倾岩质边坡 图6 不同区域位移路径 Fig.6 Displacement path of different areas

同样，反倾节理岩质边坡区域①最先产生滑动速度，随后各个条块自下而上逐渐产生滑动速度，与宏观上各区域的运动规律一致.各个岩块的起滑时间相隔很短.区域②、③的峰值总速度最大，两者非常接近，区域①的峰值总速度最小.从位移路径看，区域②、③的位移最大，水平向位移最大且基本相等，而区域①和区域④的位移相对较小.即在条形岩块倾倒破坏过程中，坡肩处岩块滑动距离最远，坡顶处岩块滑动距离次之，坡脚处岩块滑动距离最近，故应对坡肩处进行加固处理.

4 与极限平衡法对比及推广

4.1 边坡安全系数

重力增加法中边坡破坏时对应的重力加速度为临界重力加速度，边坡安全系数为边坡失稳时重力增加的倍数[21].

式中：Fs为边坡安全系数；gc为临界重力加速度；gi为初始固结重力加速度，本文中为200g.

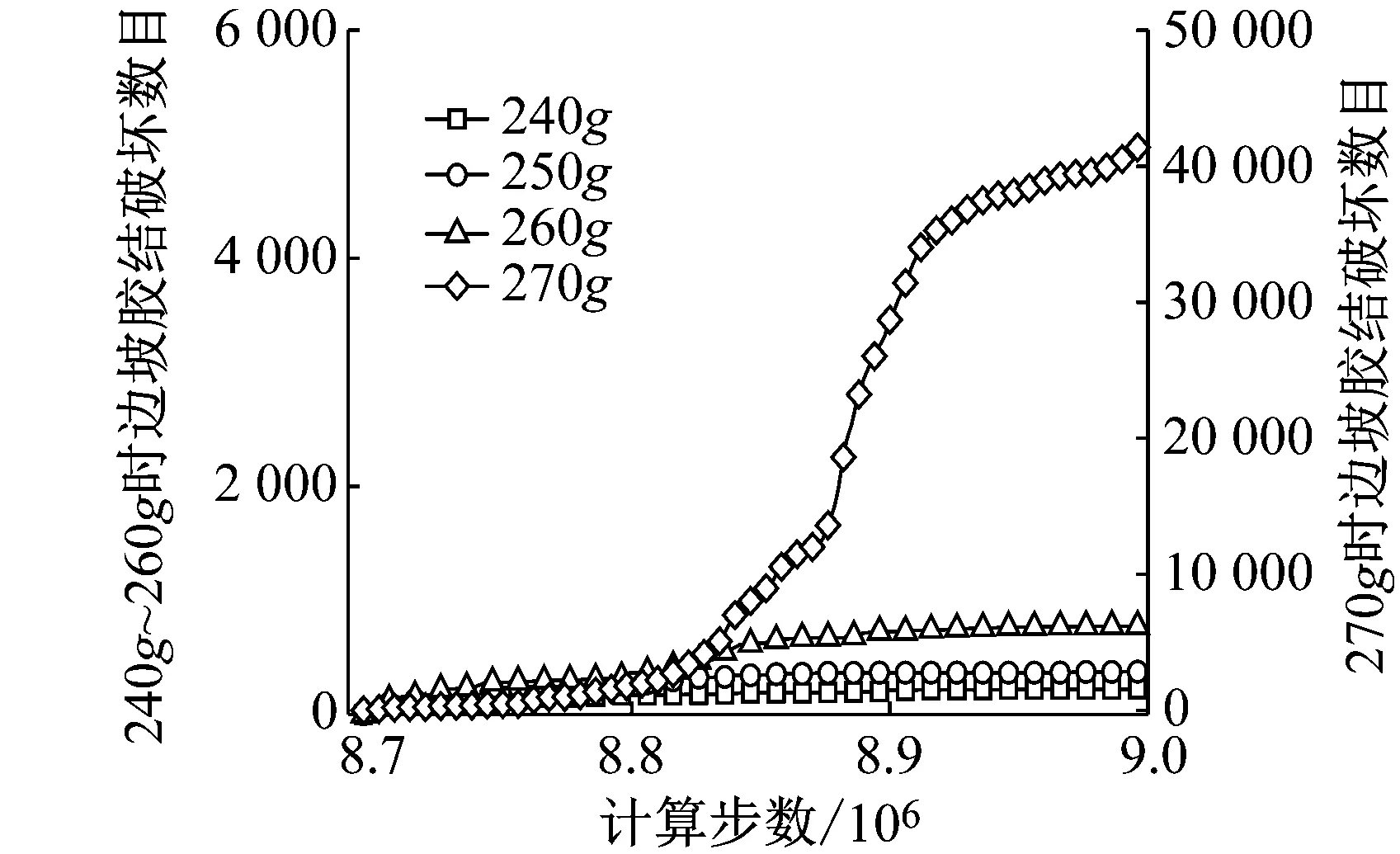
以坡角为75°的边坡为例，分别对顺层和反倾岩质边坡模型施加递增的重力场，循环计算，并记录边坡内胶结破坏的数目.典型重力场下胶结破坏数目如图7所示.在图7a中，当重力加速度从200g增加到240g后，顺层岩质边坡内胶结发生破坏，且破坏数目随着计算步数的增加而增加.随着计算步数的增加，胶接破坏数目逐渐保持稳定，边坡内部边坡裂纹不再发育，在该重力加速度下不会失稳破坏.在250g和260g重力加速度下，边坡内的胶接破坏数目有着相同的变化规律.最终，在270g重力加速度下，胶接破坏数目随着计算步数的增加而大幅增多，边坡内裂纹迅速发展，边坡失稳破坏，即270g为临界重力加速度.同理，由图7b可得出反倾岩质边坡的临界重力加速度为360g.根据边坡安全系数公式计算得坡脚为75°时顺层和反倾岩质边坡的安全系数分别为1.35和1.80.按照上述方法，进行坡脚为60°和45°的顺层和反倾岩质边坡破坏过程的离散元模拟，计算得到对应的边坡安全系数如图8所示.

a 顺层岩质边坡

b 反倾岩质边坡 图7 不同重力场作用下胶结破坏数目 Fig.7 Number of failed bonds at different gravities

对应本文不同坡角边坡的离散元计算模型，建立典型极限平衡法Morgenstern-Price法和Spencer法的边坡分析模型，并尽量保持各项参数与离散元边坡计算模型一致.运用软件Slide 5.0建模试算得到Morgenstern-Price法和Spencer法的边坡最危险滑动面，在此基础上计算得到的边坡安全系数,和离散元模拟得到的安全系数对比如图8所示.从图8中可以看出，相同坡角下，反倾岩质边坡的安全系数大于顺层岩质边坡，即反倾岩质边坡较顺层岩质边坡稳定，与工程实际的认知相同.离散元法得到的安全系数和极限平衡法相近，安全系数随边坡坡角增大而减小.即离散元法结合重力增加法可用安全系数评价边坡的安全性.

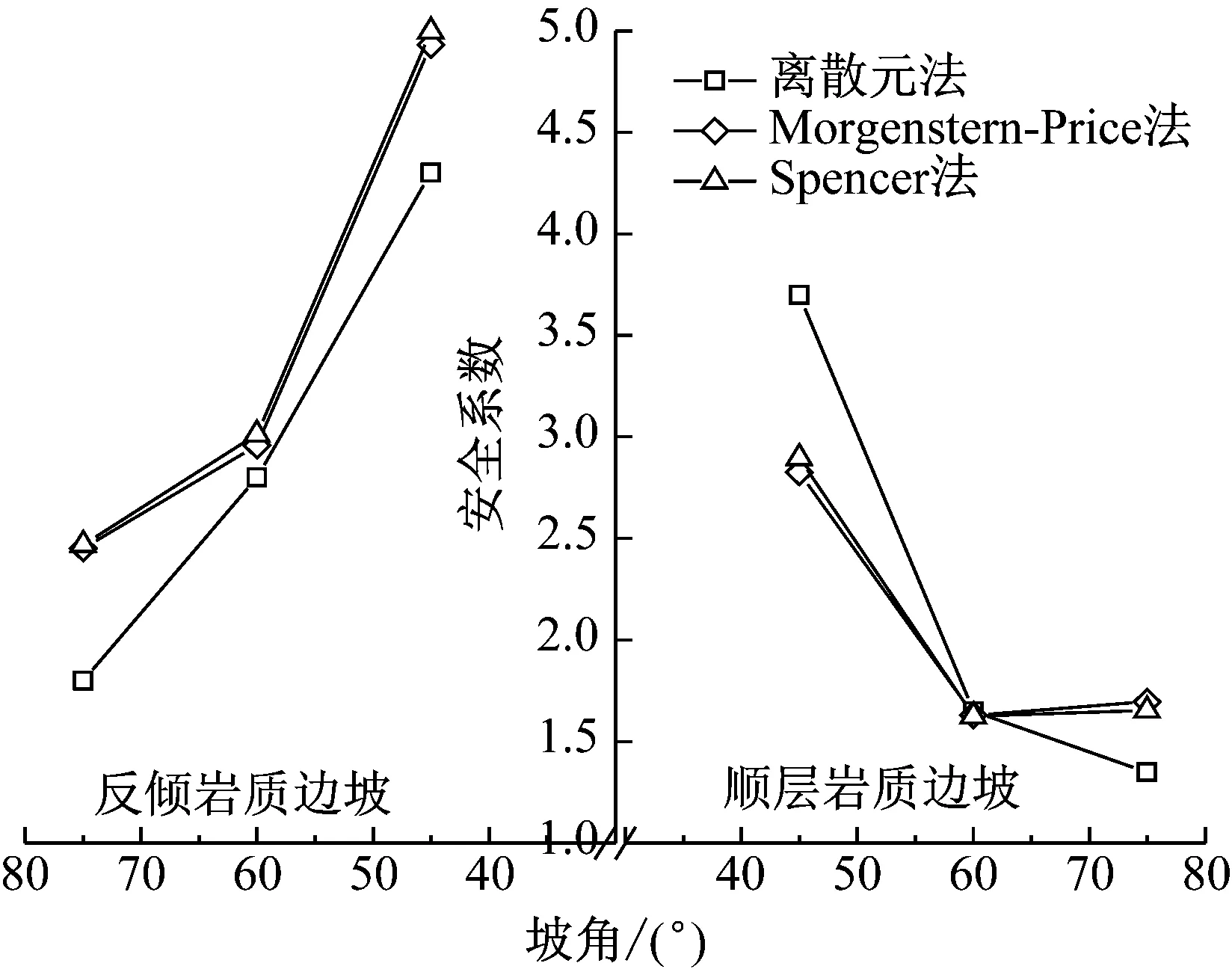
图8 DEM模拟与极限平衡法安全系数对比Fig.8 Comparison of safety factor between DEM simulation and the limit equilibrium methods

4.2 破坏模式

李祥龙等[4]通过离心机试验探讨了顺层岩体边坡的动力破坏机制，图9a为坡角为75°、节理倾角为45°顺层边坡在动力作用下的试验结果，边坡破坏时,底部的节理面发展成滑裂面①，上部岩体②沿滑裂面向下滑动.本文坡角为75°的顺层岩质边坡边界条件与之相近，结果显示顺层节理岩质边坡在重力作用下，上部岩体②沿着节理所在软弱面①发生整体顺坡向下滑动，破坏体保留一定的外部形态，本质上表现出剪切破坏，属于典型的滑动破坏模式，与李祥龙等的试验结果在定性上一致.反倾岩质边坡离散元模拟结果显示，边坡因节理切割形成相对独立岩块③，岩块在重力作用下绕下部旋转、倾倒和翻滚，形成零乱堆积物结构，属于典型的崩塌破坏模式，与图9b所示左保成等[5]的物理力学模型试验结果相似，均表现为倾倒变形折断破坏.

运用Slide 5.0 软件建立坡角为75°的边坡模型，试算确定边坡最危险滑动面，离散元法、Spencer法和Morgenstern-Price法得到的滑裂面对比如图10所示.图10中，虚线为极限平衡法的滑裂面，实线是根据离散元模拟得到的边坡滑裂面，数字为边坡安全系数.由图10可以看出，离散元模拟结果和极限平衡法求解结果基本一致.60°和45°坡角时离散元模拟滑裂面与极限平衡法得到的滑裂面对比有相同的结论.

a 顺层岩质边坡离散元模拟与离心机试验[4]对比

b 反倾岩质边坡离散元模拟与物理模型试验[6]对比 图9 边坡破坏模式 Fig.9 The failure mode of the slope

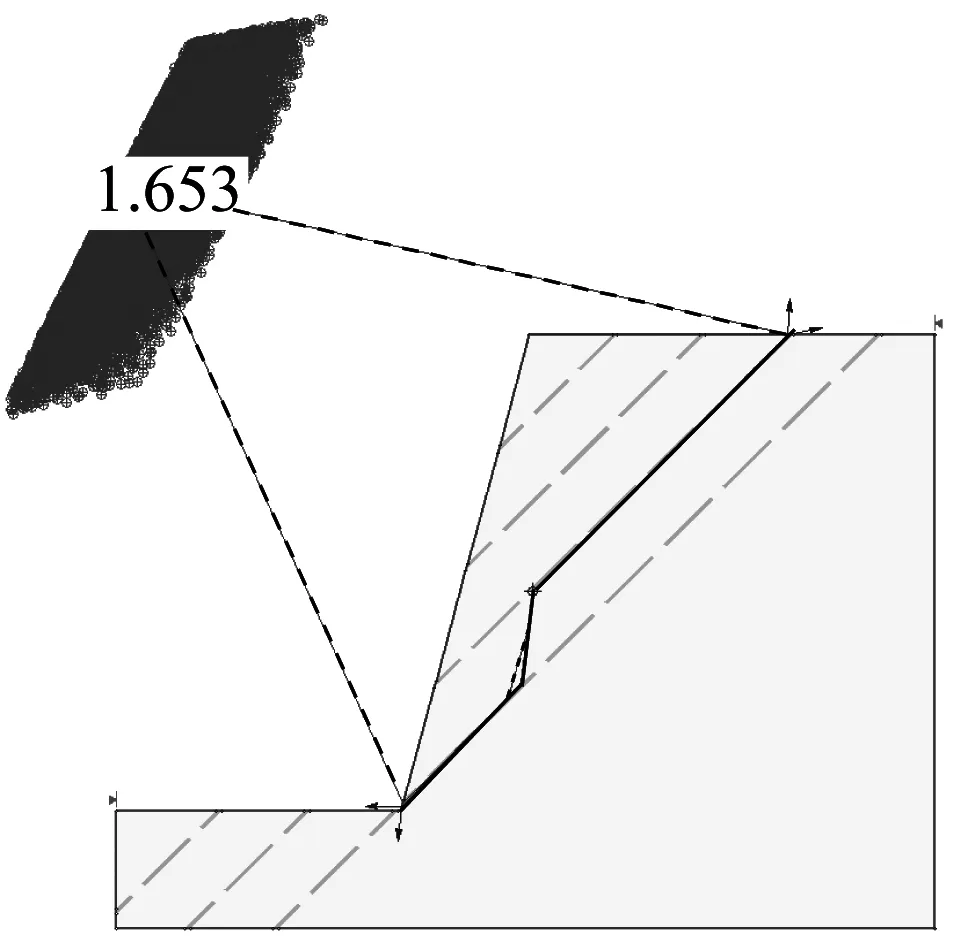
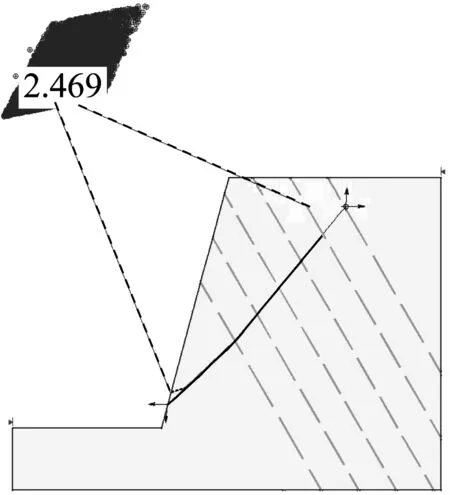
a 离散元法与Spencer法滑裂面对比

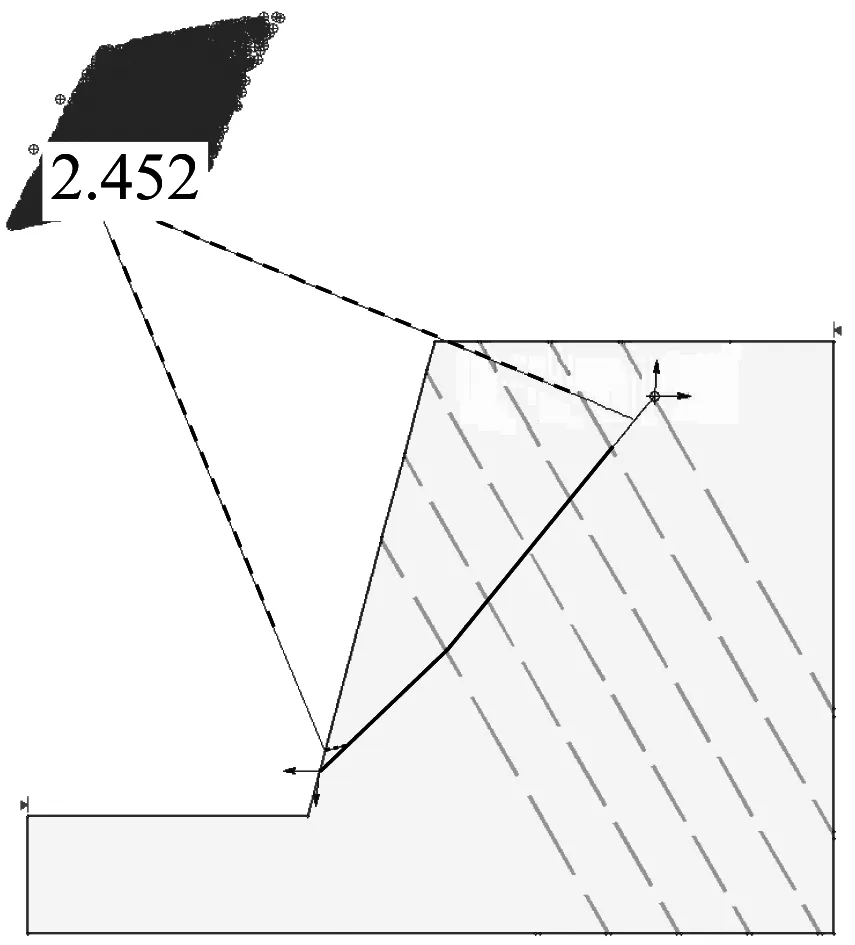
b 离散元法与Morgenstern-Price法滑裂面对比 图10 离散元法与极限平衡法滑动面对比Fig.10 Comparison of sliding surface between DEM simulations and the limit equilibrium methods

上述边坡安全系数和破坏模式的对比讨论说明，本文选取的微观参数不仅可反映岩体的宏观力学性质，还可模拟边坡的破坏演变过程和破坏形态，也可同极限平衡法一样通过安全系数评价边坡稳定性.另外，边坡的破坏是一个渐进过程[22]，极限平衡分析方法假设所有抗滑力同时发挥作用，滑动面上所有部位同时达到屈服，无法反映边坡破坏的动态过程，而离散元法数值模拟在得到滑动面的同时可观察到边坡破坏的整个过程，并获取边坡变形破坏过程中的速度场、位移场等微观信息，在边坡失稳破坏的分析上更具优越性.

5 结论

本文通过离散元数值方法模拟了顺层和反倾两种不同形式的岩质边坡破坏过程，模拟得到安全系数和滑裂面，从边坡形态、胶结破坏分布、滑体运动等方面对两种形式的边坡破坏演变过程进行了对比分析,得到以下结论：

(1) 节理形式影响边坡稳定性和破坏模式.相同条件下，顺层节理边坡较反倾节理边坡，更易产生破坏.顺层节理岩质边坡表现为共面节理发生贯通破坏，形成滑动面；反倾节理岩质边坡表现为共面节理贯通破坏将岩体分割成条形岩块，非共面节理之间发生贯通破坏，形成滑裂面.

(2) 两种形式的边坡坡脚均为薄弱区，边坡自坡脚产生裂隙，逐渐向坡顶发展，形成滑裂面，边坡加固时应优先处理坡脚区域.顺层岩质边坡需加固中部区域，反倾岩质边坡应加固坡肩区域.

(3) 离散元结合重力增加法模拟岩质边坡可通过安全系数评价边坡稳定性.与极限平衡法相比，离散元法无需滑裂面各部位同时屈服等假定，能更真实地反映岩体间的相互作用，同时可反映边坡的渐进破坏过程并获取速度场和位移路径等信息.