变曲率沟槽高精度球体精研工艺优化实验研究

, ,, ,,

(浙江工业大学 机械工程学院，浙江 杭州 310014)

陶瓷材料具有金属材料所不具备的优异性能，如高硬度、耐磨损、脆性强、密度小和化学性能稳定等，广泛应用于生活生产中的方方面面，甚至突破了原有结构陶瓷、生物陶瓷的限制，在航空航天领域以及其他高新技术领域活跃发展，其中氧化锆、氮化硅等陶瓷材料在轴承方面的应用最为广泛[1-2]。正因为陶瓷材料良好的机械性能，导致陶瓷球的加工效率较低，有效地提高陶瓷球的加工效率显得尤为重要。

陶瓷球的研磨阶段通常包括几个步骤：粗研、精研(半精研、精研和超精研)以及抛光。其中粗研阶段的主要加工目的是快速去除毛坯球表面的加工缺陷，如环带、端帽等，使球体的圆度快速收敛至1 μm左右以便后续的加工。相比粗研阶段，精研阶段的加工情况更为复杂，需要同时考虑圆度的收敛速度和球体表面粗糙的变化，并且需要及时地更换新的磨料来保持加工效率[3-4]。抛光阶段的主要目的是进一步改善球体表面质量，该阶段加工时间较短，材料去除率较低，对球体表面质量改善有限。因此如何提高球体精研阶段的加工效率是提高整个加工阶段效率的关键所在[5-6]。为提高陶瓷球的加工效率，需寻找精研阶段的最优加工参数。笔者通过软件对球体球度误差模型进行仿真，寻找最优解，而后以氧化锆陶瓷球为研究对象，采用变曲率沟槽加工方式进行实验研究，将加工时间作为评价加工效率的指标，通过优化精研阶段陶瓷球加工参数提高精研阶段球体的加工效率，对仿真结果进行验证。

1 球度误差模型的建立及其仿真

笔者提出一种基于变曲率沟槽的高精度球体加工方法[7]，在该加工方法中，用于放置球体的沟槽由传统的多个同心圆沟槽变为一条变曲率的沟槽，如图1所示。在变曲率沟槽中，由于沟槽曲线上任意一点的曲率半径都不相同，使得球体在加工过程中其自转角能够均匀连续地变化。在加工过程中，球体从沟槽盘的内部依次向外滚出，其自转角在连续变化过程中使得球体表面加工轨迹能均匀包络球体表面，再通过球体循环系统，将球体输送回沟槽盘内部，如图2所示。通过球体、磨料以及磨盘三者之间的相互作用，实现球体表面材料的机械化学去除。

图1 变曲率沟槽盘Fig.1 Variable-radius groove lapping plate

1—下研磨盘; 2—球体循环系统; 3—载荷系统; 4—变曲率沟槽盘; 5—球体; 6—主轴图2 实验装置简图Fig.2 Schematic diagram of experimental device

球体的成球条件：1) 切削等概率性；2) 尺寸选择性[8]。其中切削等概率性即球体在加工过程中其表面各个点所受到加工的概率相等，主要的评价方法是绘制球体表面加工轨迹。首先建立球体表面坐标系[7]，如图3所示。图3中：ωs为球体的自转角速度；ωg，ωb分别为2 个分量；γ，θ为其方位角。对球体进行运动学分析，计算求解主要运动参数为

(1)

(2)

(3)

式中：S为滑擦率；ρ为沟槽极径；ω为球体公转角速度；ω1为下研磨盘转速；φ为沟槽极角；rb为球体半径；β为沟槽半角。

通过Matlab数值方法求解以上方程组，解得球体的运动参数并绘制单周期球体加工轨迹，如图4所示。从图4中可以看到：在单个加工周期后，各接触点所形成的加工轨迹均能均匀地包络整个球面，并且轨迹形态在宏观上呈现多方向性，图5为加工轨迹点分布情况，轨迹点密度标准差为0.189 8。通过加工条件的进一步优化，可实现加工轨迹均匀包络整个球面，有利于实现高精度球体的精密加工。

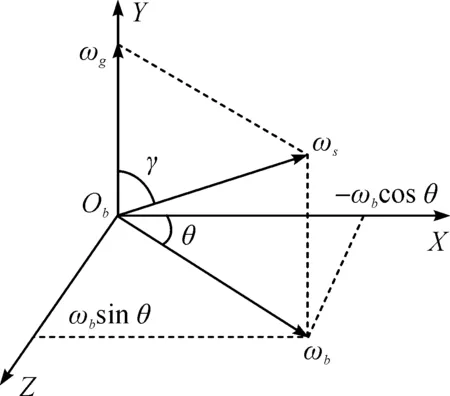
图3 球心局部坐标系Fig.3 The local coordinates of the ball

图4 单周期加工轨迹Fig.4 The processing trajectory within a single period

图5 加工轨迹点分布情况Fig.5 The distribution of track point

加工过程中球体在压力作用下与沟槽盘的接触形式为赫兹接触。通过赫兹接触理论及其经验公式可以解得球体所受应力及其应变大小[9]，其最大应力为

(4)

式中：N为接触压力；E为等效弹性模量；R，rb分别为接触区域沟槽盘半径及球体半径。

通过对工件材料[10]的研究发现：Preston方程中系数K0与工件的形状大小无关，仅与磨料相关，当磨粒为碳化硅时，磨料的粒径与系数K0的关系可表示为

y=-1.052×10-13x2+3.946×
10-11x+2.837×10-9

(5)

综上所述，将式(1～5)代入Preston方程中可解得材料去除模型为

MMR=K0pωgrb

(6)

将球体表面轨迹与球体表面材料去除率方程结合在一起，得到球体球度误差模型。其计算原理：1) 对球体表面各网格点进行初始高度赋值；2) 根据Preston方程计算接触点的材料去除量并更新高度值；3) 重新计算球度值；4) 按着研磨轨迹重复2)，3) 步至程序结束。具体仿真条件如表1所示。

表1 圆度误差仿真条件Table 1 The simulation conditions

利用Matlab对球体球度误差进行仿真，寻找合适的转阶段时机来缩短加工时间。其中最优的仿真结果为26 h，球度变化情况如图6所示。从图6中可以看出：在单个加工阶段中球度变化速率并无明显的改变，仅在加工阶段的后半段有变缓的趋势。当半精研阶段加工至0.7 μm，精研阶段加工至0.3 μm时，总加工时间最短为26 h(半精研阶段6 h，精研阶段14 h，超精研阶段6 h)，可将氧化锆陶瓷球的圆度从1 μm加工至0.2 μm。

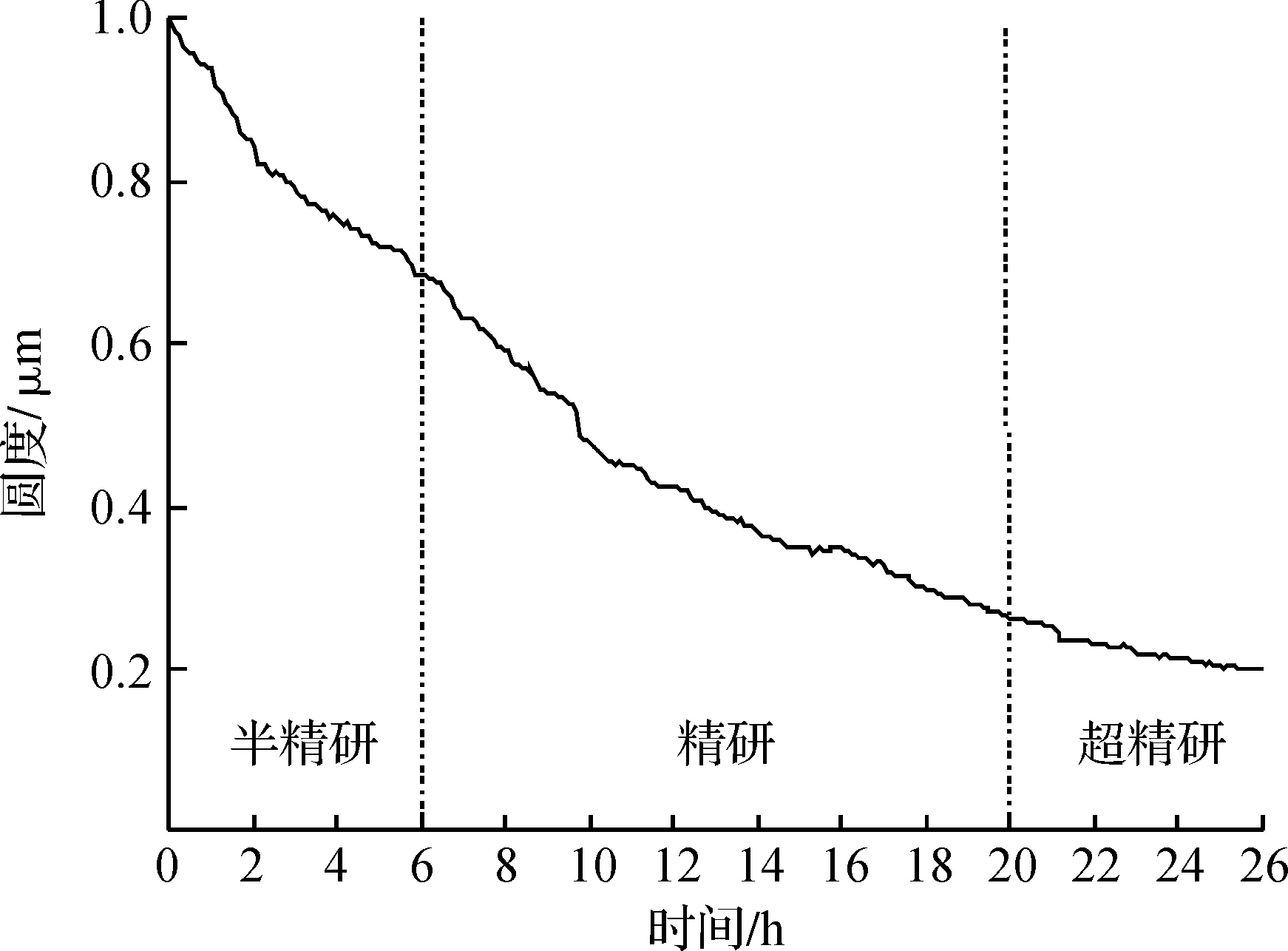
图6 不同加工阶段球度变化情况Fig.6 Variation of sphericity in different processing stages

2 研磨实验

在实际加工中考虑到加工环境的多变性，实际的材料去除率无法达到仿真结果的数值，在加工初期圆度下降速度较快，随着加工时间的增加圆度下降速度明显变慢，最后渐渐趋于稳定[11-12]，因此需要对仿真结果进行加工工艺试验验证。本次试验以φ4.763 mm的氧化锆陶瓷球为加工对象，通过变曲率沟槽加工系统对球体进行加工实验，试验条件如表2所示，其中氧化锆陶瓷球的初始粗糙度均值为930 nm，初始圆度均值为0.98 μm。在本次实验中，以加工时间为评价指标，半精研及精研加工阶段所需要达到的圆度指标为影响因素，建立L9 (34)正交[13-15]试验表。

表2 实验条件Table 2 The experimental conditions

3 实验结果及讨论

在本次实验中，通过半精研、精研以及超精研3 个阶段将球体的球度从1 μm研磨至0.2 μm，正交试验表及其结果如表3所示。表4为该正交试验的方差分析结果，从表4中可知：因素A(半精研阶段所达到的圆度)与因素B(精研阶段所达到的圆度)的F值均达到了高度显著水平，说明两者对加工时间影响的显著性较大，但是因素A的F值略大于因素B，说明半精研阶段所达到圆度的高低对实验时间的长短影响较大(权重为61.8%)，因为半精研阶段所用的磨料粒径较大，圆度收敛速度较快，想要达到更低的圆度水平(0.5，0.6 μm)需要花费更长的时间，因而对加工效率的影响更显著。

表3 正交试验实验结果Table 3 Experimental results

表4 方差分析结果Table 4 Results of ANOVA

注：1) **表示该因素对实验结果呈高度显著。

利用S-N-K法对方差分析结果进行事后检验，S-N-K法是利用水平均值大小来分析单个因素内各水平之间差异的一种方法，广泛用于方差分析的事后检验。表5为半精研阶段的S-N-K分析结果，从表5中可知：水平0.5，0.6，0.7分别位于3 个不同的子集内，说明三者之间存在差异，且差异在α=0.05水平上显著。其中水平0.7的均值最低为32.67，水平0.5的均值最大为44.33，说明在半精研加工阶段由于使用的磨料较粗，每降低0.1 μm的圆度需要的时间会更长，其中水平0.6与水平0.5的均值相差9 h，不利于提高球体加工的效率。因此半精研阶段所达到的圆度值对整体的加工时间影响较显著，这与方差分析的实验结果相吻合。

表5 半精研阶段的S-N-K分析Table 5 The S-N-K analysis results of the semi-finishing stage

表6为精研阶段S-N-K分析结果。由表6可知：水平0.3，0.4位于同一子集内，说明两者与水平0.2之间存在差异。水平0.3与0.4的均值为34.67，水平0.2的均值为43，由于球体需要继续在超精研阶段将圆度加工至0.2 μm，因此水平0.3为精研阶段最优解，即精研阶段需要达到的圆度为0.3 μm。如第8 组实验结果所示，整个加工只需要29 h，加工效率最高。

表6 精研阶段S-N-K分析Table 6 The S-N-K analysis results of the finishing stage

图7为9 组正交试验中各组圆度随加工时间变化情况。从图7中可以看出：在各加工阶段初期圆度下降速率普遍较快，这是由于更换更细的磨料，前一阶段加工所留下的缺陷被“放大”，更易被去除，圆度收敛速度较快，随着球体表面缺陷被渐渐“抚平”，圆度下降速度减缓，最后甚至需要10 h才能降低0.1 μm的圆度。从第1，4，7 组可以看出：在精研阶段后期，由于使用相同的磨料且加工条件类似，最后的圆度变化速率也都相近。在半精研阶段，当球体的圆度加工至0.7 μm时，球体的圆度变化速率已逐渐平稳并接近定值，此时若继续使用该磨料进行加工则加工效果不明显，不利于工件圆度的进一步改善，此时更换磨料进入下一加工阶段(如第7，8，9 组实验)可以大幅提升磨料的利用率，提升加工效率。而在精研阶段若在圆度约为0.4 μm时就过早地结束精研阶段反而会使得超精研加工阶段的加工时间延长，降低精研阶段的磨料利用率。综合9 组加工实验可知：当半精研阶段加工至0.7 μm，精研阶段加工至0.3 μm时(第8 组实验)，加工时间最短，加工效率最高，其所用加工时间为29 h，其中半精研阶段7 h，精研阶段15 h，超精研阶段7 h。相较于传统加工工艺，该加工工艺加工效率提高了14.7%(图8)，经过抛光之后氧化锆陶瓷球的粗糙度达到了14 nm，圆度达到了0.13 μm(图9)，达到G5级国家标准[16]。

图7 不同加工阶段圆度变化情况Fig.7 The variation of sphericity in different processing stages

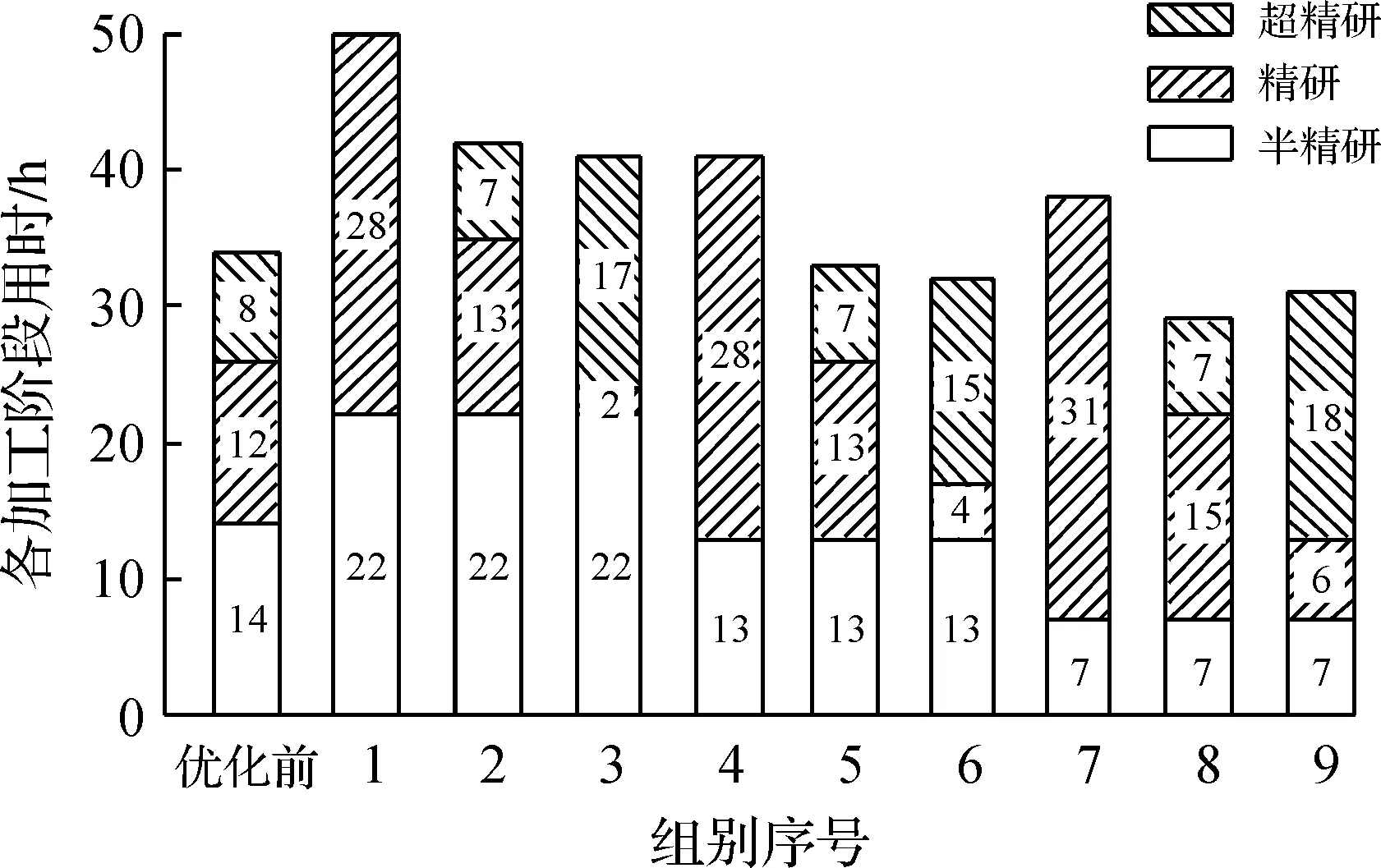
图8 优化前后加工时间对比Fig.8 Processing time before and after optimize

图9 抛光后工件表面质量Fig.9 Surface quality of the ball after polishing

4 结 论

为提高高精度陶瓷球的加工效率，对陶瓷球在变曲率沟槽加工精研阶段的加工效率进行优化，工作及结果如下：建立了变曲率沟槽球体加工方式下球体的运动学方程，并利用Matlab仿真球体表面加工轨迹情况。结果显示：各接触点所形成的加工轨迹能够均匀地包络整个球面，并且轨迹形态在宏观上呈现多方向性，有利于实现高精度球体的精密加工。基于Preston方程建立了材料去除模型，并与球体表面加工轨迹相结合建立球面球度误差仿真模型。仿真结果显示：当半精研加工阶段结束后球体球度值为0.7 μm，精研阶段结束后达到的球度值为0.3 μm时，球体加工效率最高。基于田口法设计L9(34)正交试验，并对试验结果进行方差分析及S-N-K分析。分析结果表明：半精研阶段结束后圆度与精研阶段结束后圆度对实验时长有显著影响，其中半精研阶段结束后圆度对实验时长影响较大，权重为61.8%。半精研阶段结束后圆度为0.7 μm，精研阶段结束后圆度为0.3 μm时加工效率最高，用时29 h，其中半精研阶段用时7 h，精研阶段15 h，超精研阶段7 h，加工效率提高了14.7%。采用变曲率沟槽加工方法所加工完成的氧化锆陶瓷球经抛光后，球体表面粗糙度达到14 nm，圆度达到0.13 μm，达到G5级国家标准。