水泥石水渗透系数预测的数值方法
2019-03-19,,
,,
(1.浙江工业大学 建筑工程学院,浙江 杭州 310023;2.浙江省工程结构与防灾减灾技术研究重点实验室,浙江 杭州 310023)
水泥石作为一种成分复杂的多孔材料主要由水泥水化反应生成的凝胶产物和孔隙组成,水泥石内部的孔结构直接影响水泥石的传输性能,如水渗透系数和氯离子扩散系数等。水渗透性是评价混凝土耐久性的重要指标,对混凝土材料的设计和评估起着重要的作用。在水渗透理论分析方面,国内外学者已经做了一些研究。早期的水渗透系数预测主要基于简单的孔结构模型,结合渗流理论获得近似解析解[1],该解析解主要应用于岩石等多孔材料,并不适合水泥石[2]。随着计算机技术的发展,不少学者开始借助计算机重构多孔材料的微观结构,再结合数值方法预测水渗透系数。胡浩[3]基于二维混凝土细观结构模型,引入人工压缩算法估算水渗透系数,但该方法的计算效率较低[4]。Torquato等[5]在研究多相系统平均行为时提出了随机行走方法,郑建军等[6]将该方法用于混凝土氯离子扩散系数计算,随后又基于简单多孔结构的三维模型,分析多孔材料的水渗透系数[7]。
考虑到目前各种水泥石水渗透系数预测方法的局限性,笔者在前人工作的基础上,通过在微观水平上模拟水泥石结构,再应用随机行走方法计算水泥石水渗透系数。
1 水泥水化的计算机模拟
1.1 水泥颗粒初始分布
考虑边长为a的立方体模拟单元,以不同直径的球体模拟水泥颗粒,并用Rosin Rammler函数描述水泥颗粒的粒径分布[8]。根据体视学原理,水泥颗粒粒径分布函数[9]可表示为
(1)
式中:D为水泥颗粒粒径;D0,Dm分别为最小和最大水泥颗粒粒径,对于普通水泥,D0可取1.5 μm,Dm可取10~100 μm;α0,β0为水泥颗粒的分布参数,一般分别取0.038,0.98。
根据给定的D0,Dm,a,w/c(水灰比)计算出初始水泥颗粒的体积率Vc并通过以下步骤在模拟单元内不重叠地投放初始水泥颗粒:1) 对[0, 1]上服从均匀分布的随机变量取样生成随机数pi,利用P(D)=pi求得第i颗水泥颗粒粒径Di,这一过程不断重复直到水泥体积率等于Vc;2) 将所有水泥颗粒从大到小排序;3) 对[0,a]上服从均匀分布的随机变量取样生成3个独立的随机数xi,yi,zi获得第i颗水泥的位置(xi,yi,zi),同时通过引入附加水泥颗粒施加周期性边界条件消除边壁效应[10];4) 判断第i颗水泥颗粒及其附加颗粒是否与已生成的水泥颗粒或附加水泥颗粒发生重叠,若发生重叠则回到上一步重新投放第i颗水泥颗粒,若不发生重叠则继续投放下一颗水泥颗粒。
为了直观地展示水化初期的水泥浆体的结构,设a=45 μm,w/c=0.4,D0=1.5 μm,Dm=15 μm,模拟结果如图1所示。

图1 水泥浆体结构Fig.1 Structure of cement paste
1.2 水泥水化
将水化过程中每颗水泥颗粒从内到外划分为未水化水泥层、水化产物凝胶层和“空气”层,并用rin,i(t),rout,i(t),rair,i(t)分别表示各层在t时刻的外表面半径,水化产物凝胶层厚度δi(t)=rout,i(t)-rin,i(t)。通常认为水泥水化过程由3种机理控制[8],第1种是“晶核形成和晶体生长”机理,由于这种机理比较复杂,且在水化过程中起主导作用的时间很短,可忽略不计。因此,笔者仅考虑第2,3 种机理即相边界反应机理和扩散机理对水化速度的影响。在这两种机理的控制下,单位时间Δt内未水化水泥层半径的减小量[8]可表示为

(2)
式中:H为阶跃函数;β为水化凝胶扩散系数;δtr为水化产物凝胶层临界厚度;KT为相边界反应机理主导阶段的水化速率。
在水化过程中,未水化水泥不断向内收缩,而水化产物凝胶和“空气”层不断向外膨胀,水泥颗粒间开始发生接触并互相干扰水化反应。根据水化动力学理论[8],引入参数ω0,i,ω1,i,ω2,i分别表示从内到外各层的相对未受干扰面积。先求得考虑水泥颗粒间干扰时未水化水泥体积减小量Δvc,i为

(3)
继而求得t+Δt时刻下所有水泥颗粒各层的外表面半径为

(4)
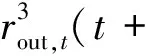
(5)

(6)

作为算例,设a=45 μm,w/c=0.4,D0=1.5 μm,Dm=15 μm,图2表示模拟单元中截面水化前与水化7,28 d时未水化水泥、水化产物凝胶和孔隙分布,它们分别用黑色、灰色和白色表示。图2表明:随着时间的增长,水化凝胶产物不断生成并开始相互干扰,各水泥颗粒和孔空间不断收缩。

图2 不同水化时间未水化水泥、水化产物凝胶和孔隙的分布Fig.2 Distribution of unhydrated cement, hydration gel, and pores at different hydration times
1.3 水化度和毛细孔隙率预测
基于水化度的定义,利用计算机模拟可以获得不同水化时间的水化度α,并与Danielession[11]的实测值对比,如图3所示。从图3可以看出:模拟值与实测值良好吻合,当水灰比等于0.3,0.5时,它们之间的相关系数分别为0.985 3,0.987 9。再应用蒙特卡罗法计算不同水化时间的毛细孔隙率φ,并与经验公式对比[12],如图4所示。图4表明:模拟值与经验公式也良好吻合,它们之间的相关系数为0.999 8。因此,模拟方法具有较高的精度。

图3 水化度预测结果与试验数据比较Fig.3 Comparison of degree of hydration between simulation results and experimental results

图4 毛细孔隙率模拟结果与经验公式比较Fig.4 Comparison of capillary porosity between simulation results and empirical formula
2 水泥石水渗透系数计算
考虑z≥0半空间上的水泥石,流体力学理论[13]表明:水在水泥石孔隙中的渗透深度L(x,y,z)和z方向上的流速u(x,y,z)均满足拉普拉斯方程,并在孔隙边界S上满足狄利克雷边界条件,即
ΔL(x,y,z)=0
(7)
L(x,y,z)S=z
(8)
Δu(x,y,z)=0
(9)
u(x,y,z)S=0
(10)

(11)
3 数值结果与讨论
为了验证随机行走算法的有效性,选择Zalzale[14]基于有效介质方法所给出的预测进行对比,当水灰比为0.4,0.5时,数值结果如图5所示。从图5可以看出:当水灰比一定时,随着水泥水化的进行,水渗透系数不断减小,这是由于水化产物凝胶不断膨胀导致毛细孔空间不断收缩,水渗透性能减弱。对于水灰比为0.4的水泥石,在水化反应的前期,笔者模拟值与Zalzale预测值吻合度较高,但当水化度大于0.8时,笔者模拟值略高于Zalzale预测值。对于水灰比为0.5的水泥石,笔者模拟值与Zalzale预测值始终良好吻合。当水灰比为0.4,0.5时,它们之间的相关系数分别为0.976 0,0.998 5。因此,笔者随机行走算法的有效性得到初步证实。

图5 水渗透系数与水化度的关系Fig.5 Relationship between water permeability coefficient and degree of hydration
为了进一步分析当水灰比为0.4时水泥石水渗透系数出现上述偏差的原因,图6给出了水渗透系数与毛细孔隙率的关系。从图6可以看出:当毛细孔隙率大于0.2时,笔者模拟值与Zalzale预测值良好吻合。当毛细孔隙率小于0.2时,笔者模拟值开始偏离Zalzale预测值,出现这一偏差的原因可能与水泥石的临界孔隙率有关。根据Bentz等[15]的研究,水泥石的临界毛细孔隙率约为0.18,当孔隙率低于0.18时,内部的毛细孔开始阻塞,孔隙间的连通性明显减弱,大部分毛细孔之间不再连通,水渗透性能也显著下降。而在水泥水化模型中,用球体来模拟水泥颗粒,这种理想化的模型导致重构的水泥石与实际水泥石之间存在偏差,当毛细孔隙率较低时,这种偏差尤为明显。因此,如何模拟非球形水泥颗粒水化全过程将成为将来研究的重点之一。

图6 水渗透系数与毛细孔隙率的关系Fig.6 Relationship between water permeability coefficient and capillary porosity
4 结 论
将微观水平上水泥石结构重构与随机行走算法相结合,预测水渗透系数。在微观水平上重构水泥石结构的过程中,将水泥颗粒模拟成各种尺寸的球体,通过与文献中水化度实测值和毛细孔隙率经验公式比较,验证了该水泥水化模型的有效性。在重构的水泥石结构上应用随机行走算法,计算水渗透系数。通过与有效介质方法比较,初步验证了笔者模拟方法的有效性,同时也发现:当孔隙率低于0.2时,笔者模拟值略高于有效介质方法预测值,产生偏差的原因可能是球形水泥颗粒假设所致,当孔隙率较低时,这种偏差尤为明显。
