类比法证明“等边对等角”和“等角对等边”

张开玲

摘 要：研究数学教学实践中用类比法证明“等边对等角”“等角对等边”及“在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半”，主要目的是在数学实际教学中通过类比法得到“等边对等角”的多种证明方法，再由这多种证明方法类比出“等角对等边”及“在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半”的多种证明方法，通过类比法贯穿教科书整小节的基本内容，充分展示类比法在数学教学中不可代替的重要地位及作用.

关键词：类比；数学教学；等边对等角；等角对等边

新的教学理念要以学生为本，采取自主讨论、自主研究、合作学习等新的模式教学.而类比法就是数学实际教学中促成这一模式的一种有效的方法，在数学教学实践中，引导学生应用这一方法可达到事半功倍的效果.

一、证明“等边对等角”

实际教学中，在证明“等边对等角”时，教科书给出的证明方法是通过作等腰三角形底边上的中线，具体如下：

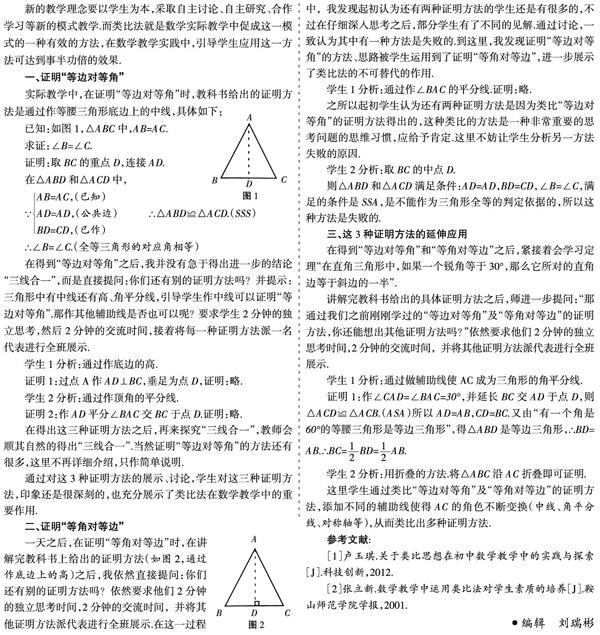
已知：如图1，△ABC中，AB=AC.

求证：∠B=∠C.

证明：取BC的重点D，连接AD.

在△ABD和△ACD中，

∵AB=AC，（已知）AD=AD，（公共边） ∴△ABD≌△ACD.（SSS）BD=CD，（已作）

∴∠B=∠C.（全等三角形的对应角相等）

在得到“等边对等角”之后，我并没有急于得出进一步的结论“三线合一”，而是直接提问：你们还有别的证明方法吗？并提示：三角形中有中线还有高、角平分线，引导学生作中线可以证明“等边对等角”.那作其他辅助线是否也可以呢？要求学生2分钟的独立思考，然后2分钟的交流时间，接着将每一种证明方法派一名代表进行全班展示.

学生1分析：通过作底边的高.

证明1：过点A作AD⊥BC，垂足为点D，证明：略.

学生2分析：通过作顶角的平分线.

证明2：作AD平分∠BAC交BC于点D.证明：略.

在得出这三种证明方法之后，再来探究“三线合一”，教师会顺其自然的得出“三线合一”.当然证明“等边对等角”的方法还有很多，这里不再详细介绍，只作简单说明.

通过对这3种证明方法的展示、讨论，学生对这三种证明方法，印象还是很深刻的，也充分展示了类比法在数学教学中的重要作用.

二、证明“等角对等边”

一天之后，在证明“等角对等边”时，在讲解完教科书上给出的证明方法（如图2，通过作底边上的高）之后，我依然直接提问：你们还有别的证明方法吗？依然要求他们2分钟的独立思考时间，2分钟的交流时间，并将其他证明方法派代表进行全班展示.在这一过程中，我发现起初认为还有两种证明方法的学生还是有很多的，不过在仔细深入思考之后，部分学生有了不同的见解.通过讨论，一致认为其中有一种方法是失败的.到这里，我发现证明“等边对等角”的方法、思路被学生运用到了证明“等角对等边”，进一步展示了类比法的不可替代的作用.

学生1分析：通过作∠BAC的平分线.证明：略.

之所以起初学生认为还有两种证明方法是因为类比“等边对等角”的证明方法得出的，这种类比的方法是一种非常重要的思考问题的思维习惯，应给予肯定.这里不妨让学生分析另一方法失败的原因.

学生2分析：取BC的中点D.

则△ABD和△ACD满足条件：AD=AD，BD=CD，∠B=∠C，满足的条件是SSA，是不能作为三角形全等的判定依据的，所以这种方法是失败的.

三、这3种证明方法的延伸应用

在得到“等边对等角”和“等角对等边”之后，紧接着会学习定理“在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半”.

讲解完教科书给出的具体证明方法之后，师进一步提问：“那通过我们之前刚刚学过的“等边对等角”及“等角对等边”的证明方法，你还能想出其他证明方法吗？”依然要求他们2分钟的独立思考时间，2分钟的交流时间，并将其他证明方法派代表进行全班展示.

学生1分析：通过做辅助线使AC成为三角形的角平分线.

学生2分析：用折叠的方法.将△ABC沿AC折叠即可证明.

这里学生通过类比“等边对等角”及“等角对等边”的证明方法，添加不同的輔助线使得AC的角色不断变换（中线、角平分线、对称轴等），从而类比出多种证明方法.

参考文献：

[1]卢玉琪.关于类比思想在初中数学教学中的实践与探索[J].科技创新，2012.

[2]张立新.数学教学中运用类比法对学生素质的培养[J].鞍山师范学院学报，2001.