一粒沙里见世界，小公式里见真章

方书英

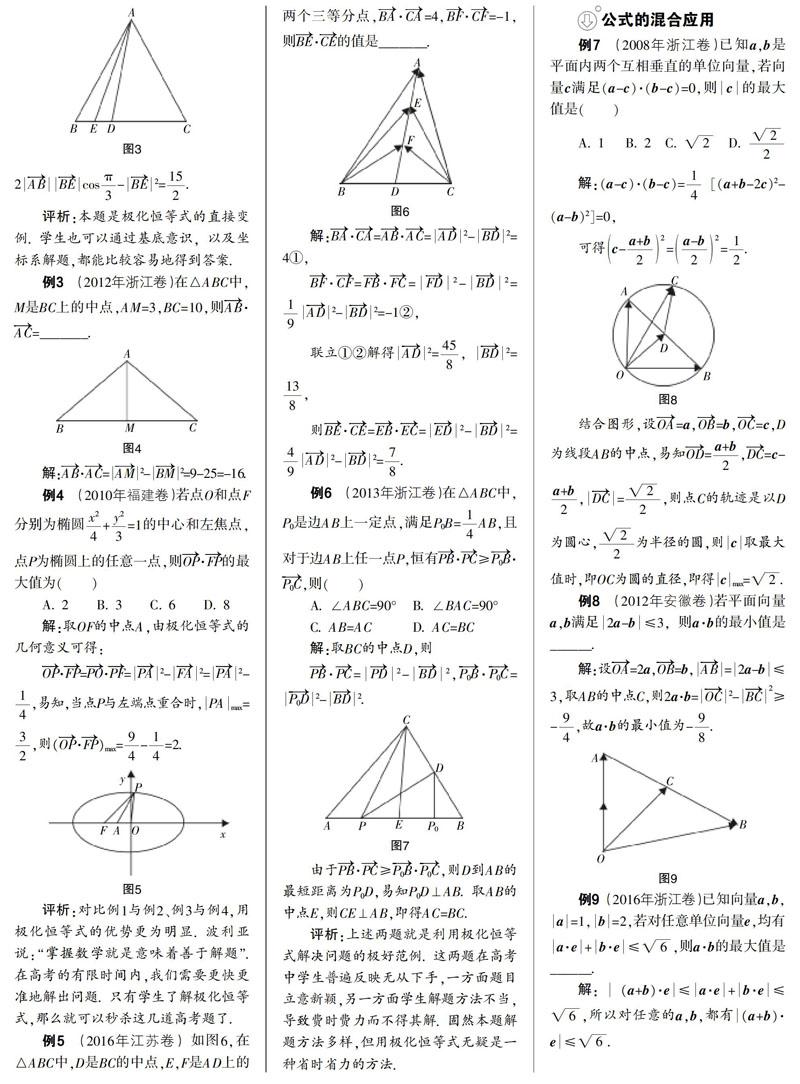
[摘  要] 自2003年高考中增添向量题以来，浙江省的向量题难度一向较高. 极化恒等式来源于教材，又高于教材. 某些向量高考题可用极化恒等式来处理. 在有些问题中，极化恒等式有较为明显的优势.

[关键词] 平面向量;极化恒等式;高考真题.

自2003年高考增添平面向量问题以后，向量题就成了高考中的创新题的热点，命题也有越来越综合、灵活的趋势. 尤其是浙江省的向量问题难度颇高，经常作为客观题的压轴题出现. 笔者在一所普通高中任教数年，深感学生对向量问题的困惑. 面对繁多的解法，学生反而不知道从何下手，种种浅尝辄止之后，往往是敬而遠之. 在连续的两年高三数学的教学生涯中，大量习题的演练之下，笔者发现有一些小技巧可以帮助学生解题，在多次练习巩固之后，部分学生也能解决一些稍有难度的问题. 本文主要讨论极化恒等式在解题中的应用. 综观历年各省市的高考题，发现能用极化恒等式解决的题目数量颇多. 在百花齐放的各种解题方法中，极化恒等式在解决某些较难的向量题时有较强的灵活性和技巧性. 运用得当，可以节约学生们宝贵的答题时间，并进一步提高学生的答题准确率.

反思

向量是沟通代数和几何的纽带，向量的坐标运算深刻反映向量的代数性质，相对来说，向量的几何性质应用较少，但是极化恒等式的应用比较好地弥补了这个缝隙. 将向量的数量积和向量的模联系起来，而使得“秒杀”一类向量高考题成为可能. 我们用极化恒等式解决问题，也不是为了追求高难度的解题技巧，而是要在教学过程中教会学生选择合理的解题方法，揭示问题的本质，从而达到提高自己整体解题水平的目的.