激光光路控制电磁作动器的模糊PID控制特性分析

孙凤， 张琪， 徐方超， 李强， 金俊杰， 佟玲， 张晓友， 刘巍巍

(沈阳工业大学 机械工程学院， 辽宁 沈阳 110870)

0 引言

激光在工业领域中主要被应用于切割、焊接、3D打印、标记和热处理等领域[1]。传统激光切割过程中，辅助气体喷射中轴线始终与激光焦点中轴线同轴，Quintero等[2]通过实验验证了改变辅助气体喷射中轴线与激光焦点中轴线角度可以提高切割效率与切口质量。从空气动力学角度分析，不改变辅助气体喷射中轴线与激光焦点中轴线角度，只改变二者相对位置，即辅助气体喷射中轴线与激光焦点中轴线不同轴也能达到提高加工工件质量和加工速度的目的。但这需要一种结构紧凑、响应速度快的作动器来实现激光焦点中轴线位置的实时控制。

传统驱动平台由于体积大、响应速度慢、噪声大等缺点，以致很难达到理想的控制精度。磁悬浮技术因具有无接触、无摩擦、无磨损、不需要密封和润滑等优点，被应用于定位精度高、响应速度快的驱动领域[3-5]。Molenaar 等[6]设计了一种TU型6自由度磁悬浮定位平台，U型结构作为定子，T型结构缠有线圈作为动子在U型结构内运动产生水平推力，悬浮力由定子上3个悬浮线圈产生。陈本永等[7]设计了一种磁悬浮微动平台，建立了电磁驱动数学模型，并运用MATLAB软件进行了运动特性分析，为磁悬浮微动平台的设计和研究提供了理论基础。李群明等[8]根据设计好的磁悬浮平台，建立了系统动力学方程和机电耦合动力学模型，并根据机电耦合动力学模型对平台稳定性进行了分析，得到了平台稳定时悬浮控制的参数范围，从而证明了采用磁悬浮技术控制平台具有良好的动态性能和静态性能。

为了实时控制辅助气体喷射中轴线与激光焦点中轴线的相对位置，本文设计了一种结构紧凑、响应速度快、无需润滑的电磁作动器。若采用传统PID控制算法，由于电磁作动器电磁力是电流和气隙的非线性函数，难以建立起精确的数学模型。而采用模糊PID控制算法无需建立精确的数学模型，并且可以获得较好动态性能[9-11]。结合电磁作动器和模糊PID控制算法的优点[12-16]，本文设计了一种模糊PID控制的电磁作动永磁复位式3自由度电磁作动器。

1 电磁作动器结构与数学模型

1.1 电磁作动器结构

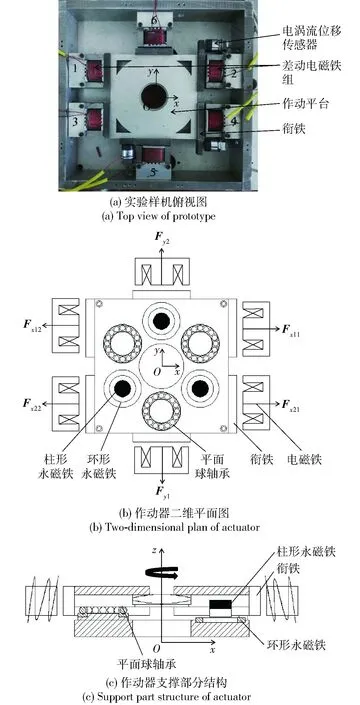
图1 电磁作动器实验的作动平台Fig.1 Experimental prototype of electromagnetic actuator

电磁作动器作动平台结构如图1所示。图1(a)为3对差动电磁铁的差动结构布置。图1(b)为电磁作动器二维平面图，包括圆柱形永磁铁、环形永磁体、平面球轴承、电磁铁和衔铁，其中Fx11、Fx12、Fx21、Fx22分别为作动平台运动过程中x轴方向2对差动电磁铁电磁力，Fy1、Fy2分别为y轴方向1对差动电磁铁电磁力。图1(c)为电磁作动器支撑部分结构，由平面球轴承、环形永磁铁和圆柱形永磁铁组成。其中，轴线同心、同极相对的轴向磁化环形永磁体和圆柱形永磁体组成的永磁弹簧结构为3组，与平面球轴承均匀分布。每组永磁弹簧在z轴方向上表现为吸引力，在x轴和y轴方向上表现为排斥力，从而可以保证电磁铁断电时，在x轴和y轴方向上平台可以自动回复到初始位置。

1.2 电磁作动器作动平台数学模型

如图2所示：根据作动平台结构，选取初始位置质心O(x，y，θ)为坐标原点，其中，θ为作动平台绕质心转动的角度；作动平台运动过程中，圆柱形永磁体和环形永磁体之间回复力分别为Fm1、Fm2、Fm3，平面球轴承与作动平台上顶盖之间摩擦力为f. 电磁铁电磁力、圆柱形永磁铁和环形永磁铁之间回复力及平面球轴承与作动平台上顶盖之间摩擦力共同作用，使得作动平台做Oxy平面内的平动和绕作动平台质心的转动，作动平台质心偏离到O′(x1，x2，y)位置。根据作动平台结构、物理参数和力学特性，令位移传感器与衔铁之间气隙相对增大方向为正，作动平台绕质心逆时针旋转方向为正。

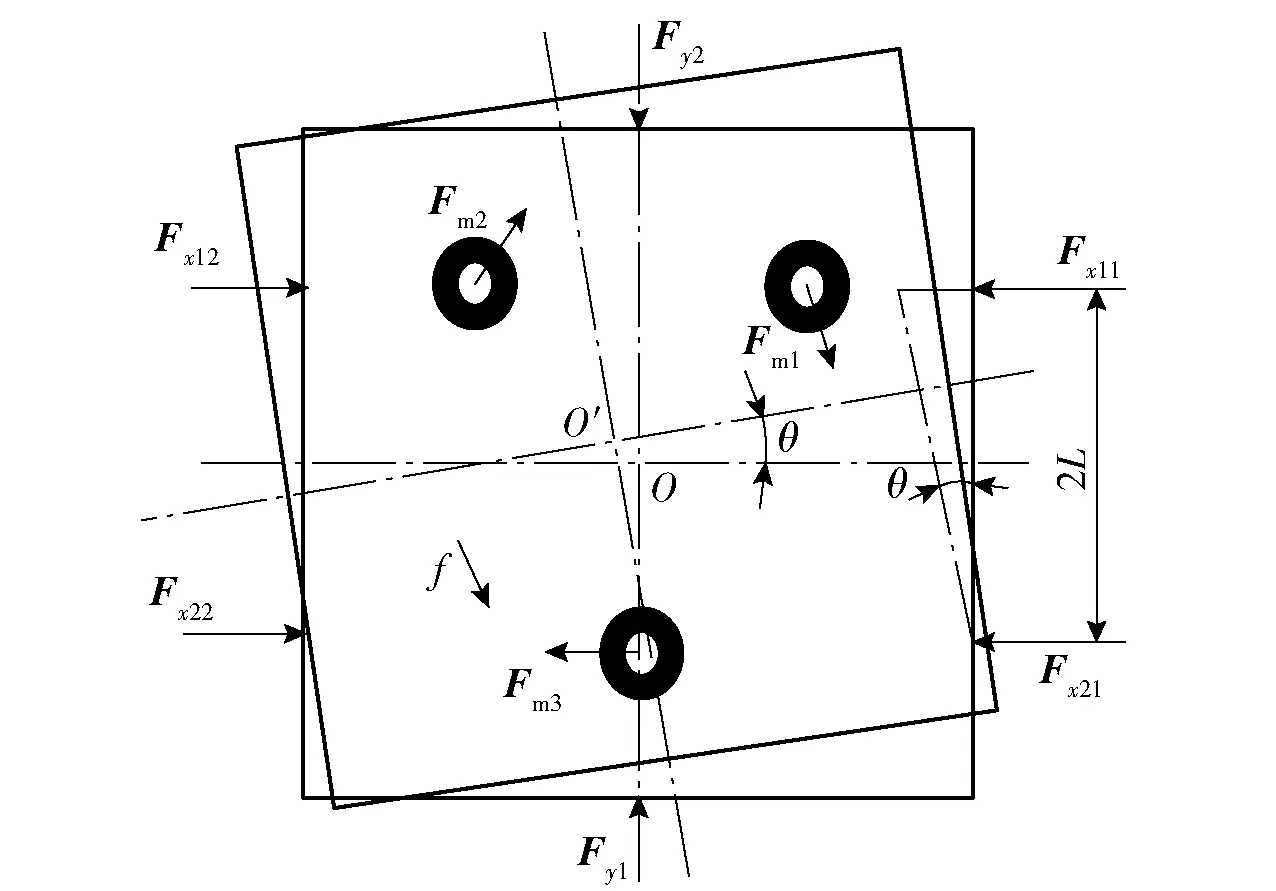
图2 电磁作动器受力分析图Fig.2 Force analysis chart of electromagnetic actuator

设初始质心O广义坐标为

(1)

作动平台3对电磁铁和3个位移传感器广义坐标为

(2)

两坐标之间的变换关系为

(3)

式中：x1为图1(a)电磁铁2上方位移传感器检测到的数值；x2为图1(a)电磁铁4下方位移传感器检测到的数值；L为电磁铁2和电磁铁4两侧位移传感器之间的距离。

1对差动电磁铁驱动力[17]为

Fx1=kii+kxx，

(4)

式中：ki和kx分别为电流刚度系数和x轴方向位移刚度系数；i为差动电磁铁中的电流值。

经过仿真分析和实验验证，圆柱形永磁体和环形永磁体组成的永磁弹簧结构径向磁力与径向位移之间关系如图3所示。当径向位移较小时，永磁弹簧结构径向磁力随着径向位移的增加而增加，所产生径向回复力与径向位移可近似看作线性关系，即

Fm=ktδ，

(5)

式中：Fm为1对圆柱形永磁体与圆环形永磁体之间的径向回复力；kt为磁弹簧刚度系数；δ为径向位移。

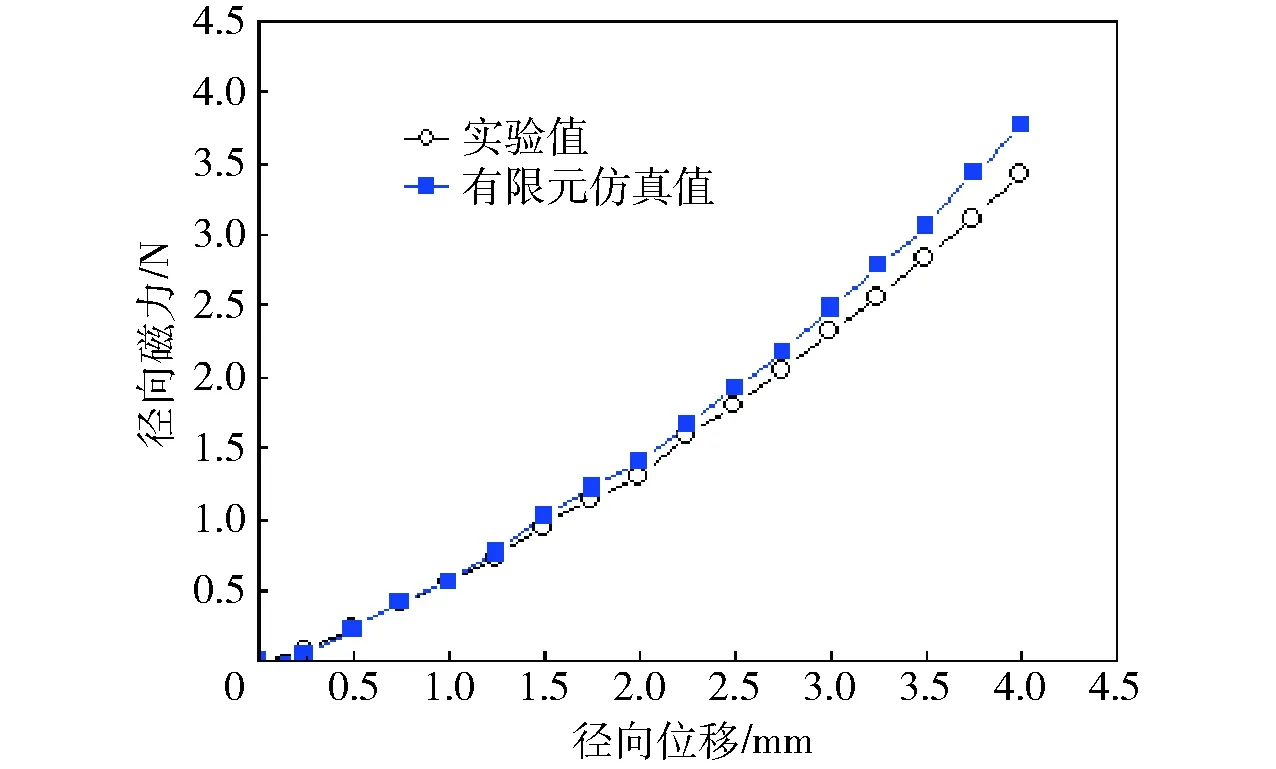
图3 径向磁力与径向位移关系Fig.3 Relationship between radial magnetic force and radial displacement

系统运动方程为

(6)

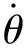
根据系统动力学方程建立系统状态空间方程为

(7)

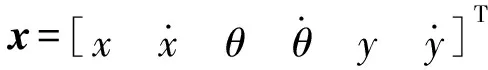
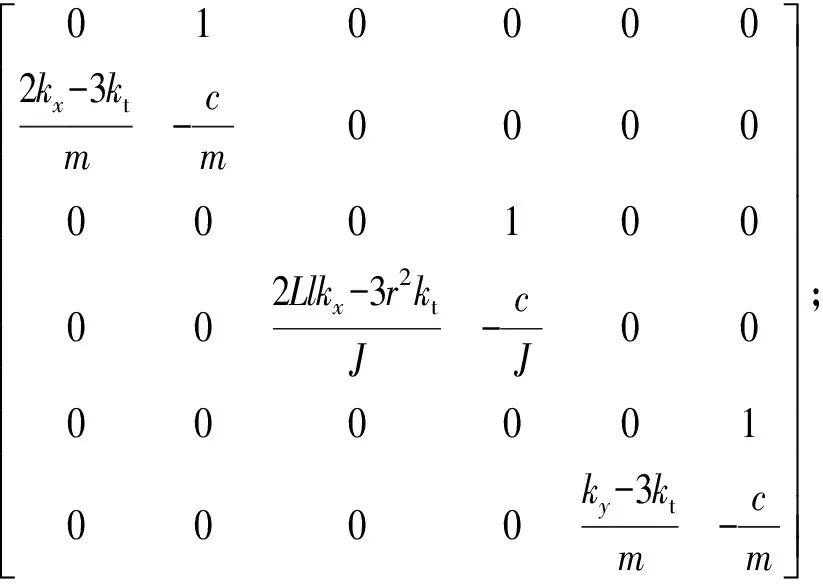
作动平台结构参数如表1所示。

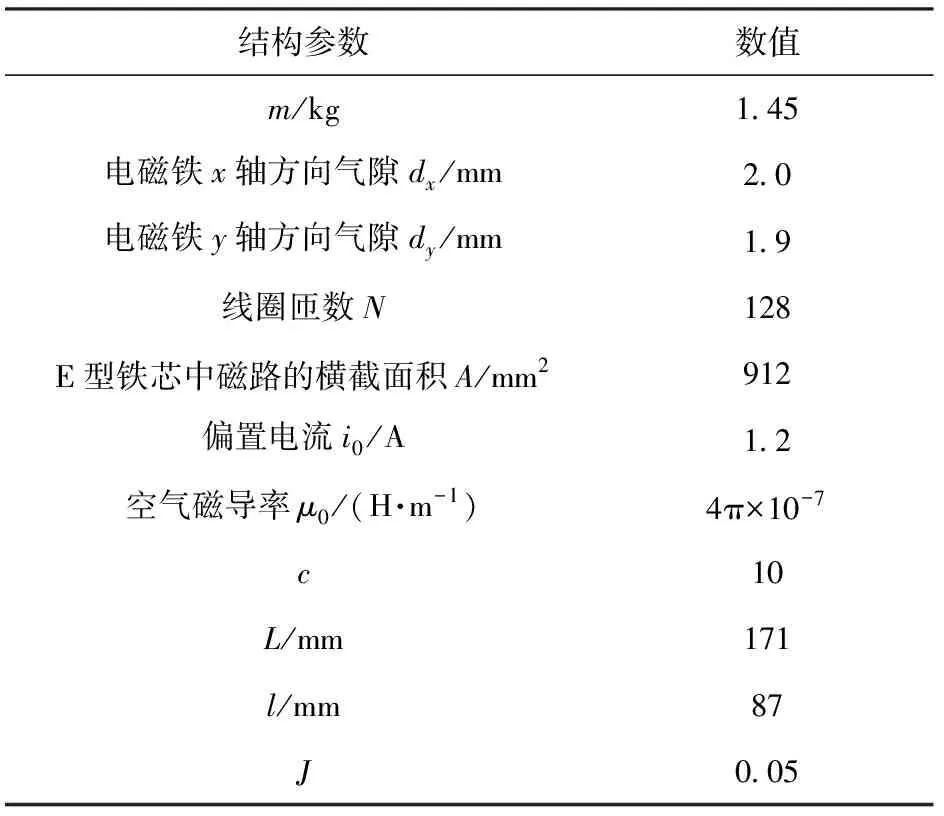
表1 作动平台结构参数

2 模糊PID控制器设计

2.1 论域和隶属函数设计

模糊PID控制器被控对象无需建立精确数学模型，在传统PID控制器基础上，以位置偏差e和位置偏差变化率ec作为模糊PID控制器输入，采用模糊推理方法对PID参数kP、kI、kD进行调节，来满足不同e和ec对控制系统的要求，从而使被控系统具有良好的动态性能和静态性能。根据电磁作动器特点，本文模糊PID控制器以e和ec作为控制器输入，PID参数变化量ΔkP、ΔkI、ΔkD作为控制器输出，结合作动平台利用模糊规则对PID参数进行在线调整，如图4所示。

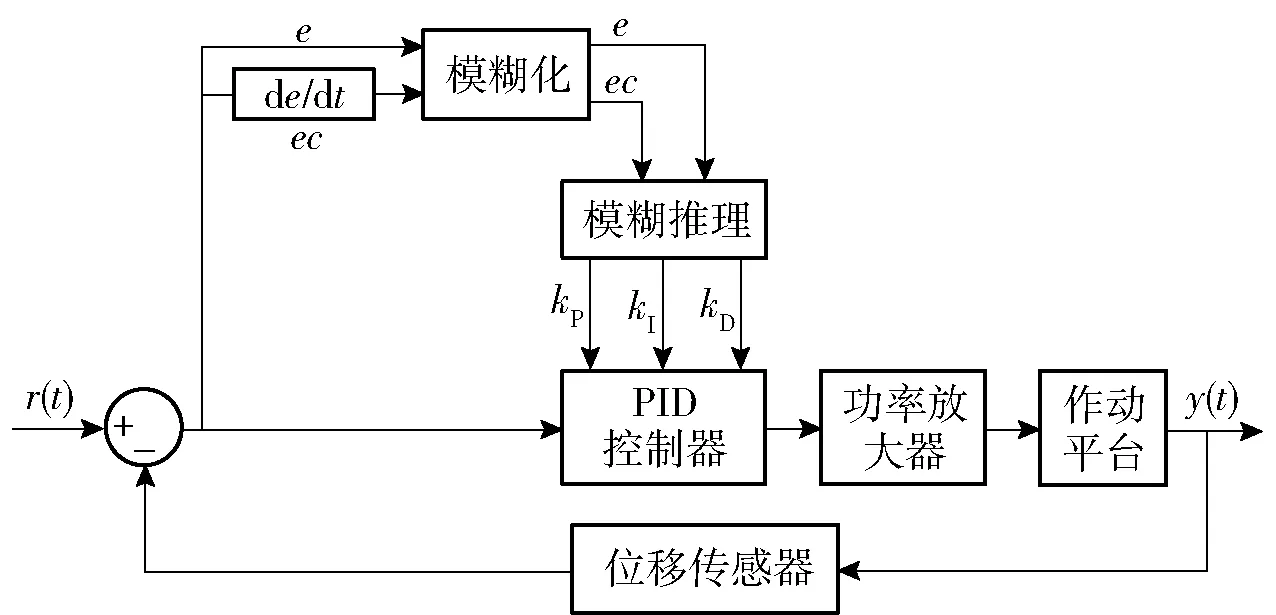
图4 模糊PID控制器结构图Fig.4 Structure diagram of fuzzy PID controller

根据作动平台实际情况，本文模糊PID控制器采用均匀的三角形隶属度函数，并用Mamdani方法进行模糊推理。采用重心法对模糊推理所得位移进行模糊判决，从而得到位移精确值，再乘以比例因子输出位移实际值。将实际值与反馈位移比较得到作动平台的e，将e和ec输入到参数自校正模糊PID控制器中，在线运行过程中，控制系统通过对模糊规则的查表和运算，完成对PID参数的在线自校正。

模糊PID控制器输入e、ec和输出ΔkP、ΔkI、ΔkD的模糊子集定义分别为

e=ec={NB NM NS ZO PS PM PB}，
ΔkP=ΔkI=ΔkD={NB NM NS ZO PS PM PB}，

式中：NB、NM、NS、ZO、PS、PM、PB分别为负大、负中、负小、0、正小、正中、正大；模糊控制器e、ec的实际变化范围称为其基本论域，e和ec的论域为(-6，6)，ΔkP、ΔkI、ΔkD的论域为(-6，6).

2.2 量化因子、比例因子的确定

在进行模糊化运算时，需要将e、ec等变量的基本论域转化为相应模糊论域，因此需要引入量化因子。同理，在经过模糊PID控制器处理后，需要将处理后变化量的模糊论域变成实际控制对象的基本论域，中间需要一个比例因子。而量化因子和比例因子的选择与PID参数、作动平台的动态性能有关，作动平台输入e的基本论域为[-3,3]，模糊论域为[-6,6]，则其量化因子为6/3=2. 同理，根据作动平台特性，输入ec量化因子取值为0.01，输出ΔkP、ΔkI、ΔkD比例因子取值分别为5、20、0.000 6.

2.3 模糊规则的确定

调节前期，e较大时，为了使作动平台获得较快响应速度，取较大kP，由于开始时e有可能瞬时变大而导致微分过饱和，使控制作用超出控制范围。为防止衔铁被电磁铁吸引，应取较小kD，同时为了防止出现较大超调，产生积分饱和，应对积分作用加以限制，一般取kI=0. 当e和ec处于中等大小时，为了使系统具有较小超调，kP取值应适中；为了避免影响稳定性，kI取值应适中；这时kD取值对系统控制特性影响比较敏感，kD取值应适当减小。

当e较小、快接近给定值时，为了使系统具有较好稳定性能，应减小kP取值来减少静差，抑制超调，同时应适当增加kI取值。为了在给定值附近出现振荡现象，并考虑系统抗干扰性能，这时kD取值非常重要。一般来说，当ec较小时，kD取值应大一些；当ec较大时，kD取值可小一些。根据上述规律和实际操作经验，可制定出针对PID参数ΔkP、ΔkI、ΔkD模糊控制规则，如表2所示。

表2 参数ΔkP、ΔkI、ΔkD控制规则调整表

3 仿真分析

激光切割机焦点控制系统的电磁作动器整体控制框图如图5所示。电磁铁1与电磁铁2，电磁铁3与电磁铁4，电磁铁5与电磁铁6分别构成3对差动电磁铁，其中，电磁铁1与电磁铁2，电磁铁3与电磁铁4一起控制作动平台x轴方向平动和绕质心转动，电磁铁5与电磁铁6控制作动平台y轴方向平动。首先电涡流位移传感器将测量到的位移信号传给该系统核心处理器dSPACE1103，通过 Controldesk与MATLAB/Simulink连接，得到偏差信号作为模糊PID控制器的一个输入，控制功率放大器中的电流大小，并实现对每对差动电磁铁的实时控制。根据模糊PID控制器结构和原理，选择在MATLAB/Simulink环境下分别对x轴方向、y轴方向进行仿真。

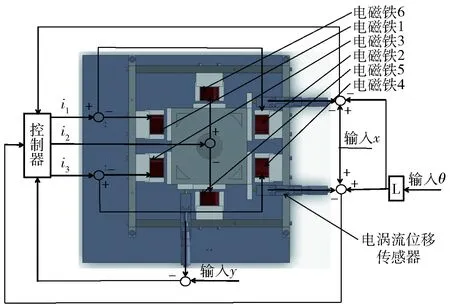
图5 系统控制结构图Fig.5 Control structure diagram of the proposed system

3.1 传统PID控制器x轴方向位置响应仿真分析

根据作动平台建立数学模型，参考线性二次型调节器(LQR)最优控制策略，通过试凑法进行调节，最终得到相对最优控制参数。传统PID控制器参数kP、kI、kD取值分别为2 754、10 000、10时，传统PID控制器x轴方向位置响应仿真结果如图6所示。

由图6可见，0.20 s时，给作动平台x轴方向一个0.10 mm位移阶跃信号，作动平台向左运动并在0.35 s保持稳定。作动平台响应时间为0.15 s，作动平台位置由0 mm到0.13 mm最后稳定在0.10 mm，由此可知，传统PID控制器x轴方向平动最大超调量为30%.由于作动平台为平动，控制电流都是从0 A开始先增加最后趋于稳定。从中可以看出，传统PID控制器可以使作动平台在x轴方向实现稳定控制。

3.2 模糊PID控制器x轴方向位置响应仿真分析

根据作动平台参数和LQR控制策略，通过试凑法进行调节，最终得到相对最优控制参数。模糊PID控制器参数kP、kI、kD取值分别为2 754、10 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6时，模糊PID控制器x轴方向位置响应仿真结果如图7所示。

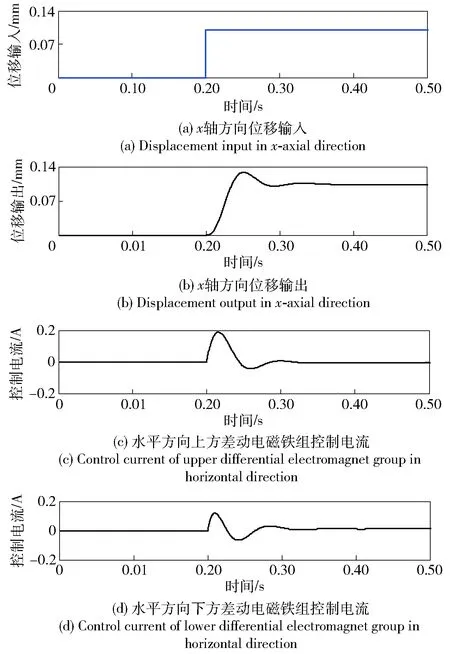
图7 模糊PID控制器x轴方向仿真结果Fig.7 Simulated results of fuzzy PID controller in x-axial direction

由图7可见，0.20 s时，给作动平台x轴方向一个0.10 mm位移阶跃信号，作动平台向左运动。作动平台响应时间为0.15 s，作动平台位置由0 mm最后到0.10 mm，最大位置在0.13 mm，模糊PID控制器平动x轴方向位置响应超调量为30%. 由于作动平台是平动，控制电流变化趋势是相同的。从中可以看出，模糊PID控制器可以使作动平台在x轴方向实现稳定控制。

3.3 传统PID控制器y轴方向位置响应仿真分析

根据作动平台建立数学模型，参考LQR控制策略，通过试凑法进行调节，最终得到相对最优控制参数。将传统PID控制器参数kP、kI、kD分别取10、22 000、0.01，y轴方向传统PID控制器仿真结果如图8所示。0.20 s时，给作动平台y轴方向一个0.10 mm位移阶跃信号，作动平台向上运动。作动平台响应时间为0.60 s，位移最大变化量为0.11 mm，位移响应最大超调量为10%，控制电流由0 A变化到0.30 A最后趋于0 A稳定。从中可以看出，传统PID控制器可以使作动平台在y轴方向实现稳定控制。

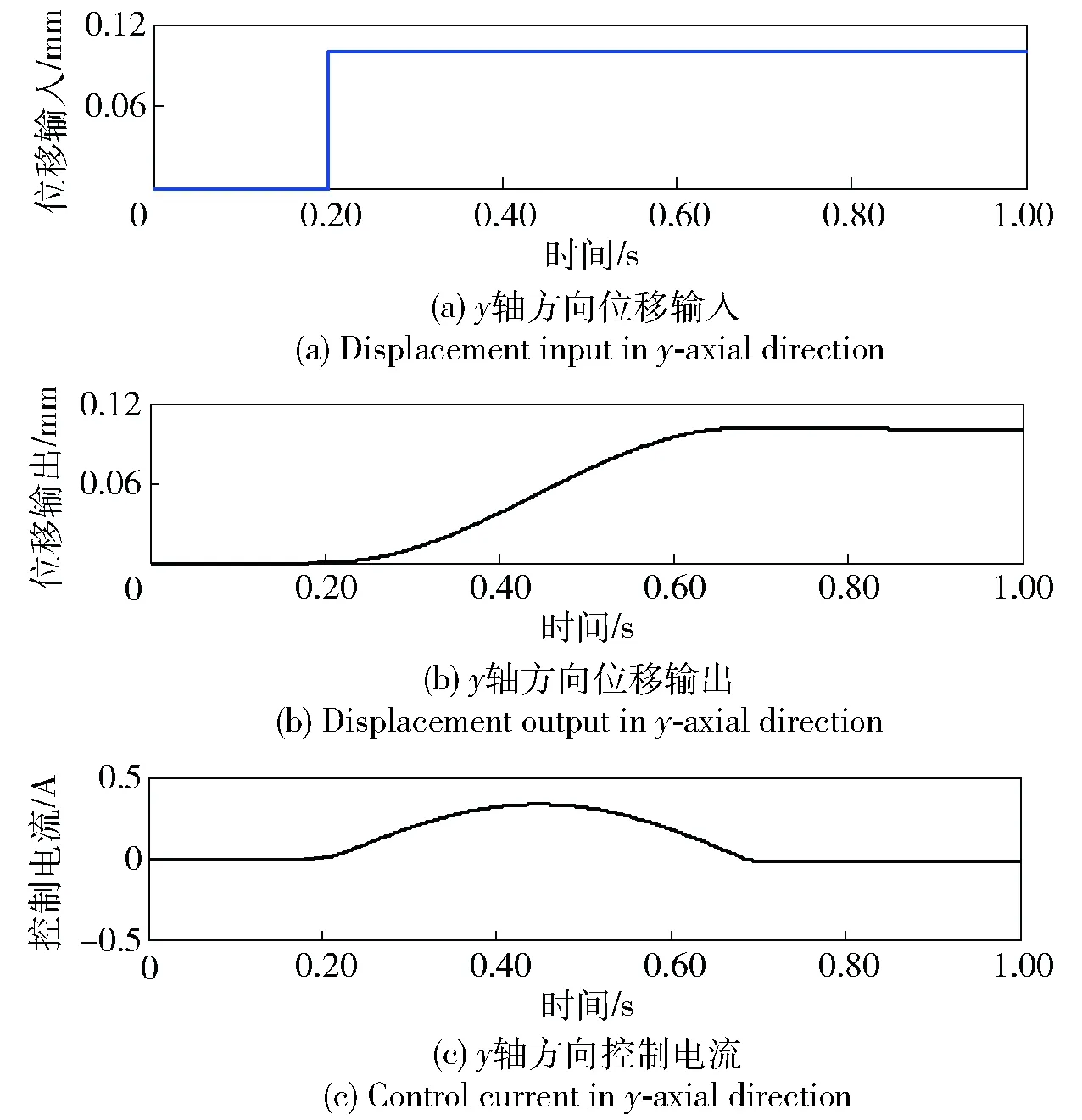
图8 传统PID控制器y轴方向仿真结果Fig.8 Simulated results of traditional PID controller in y-axial direction

3.4 模糊PID控制器y轴方向位置响应仿真分析

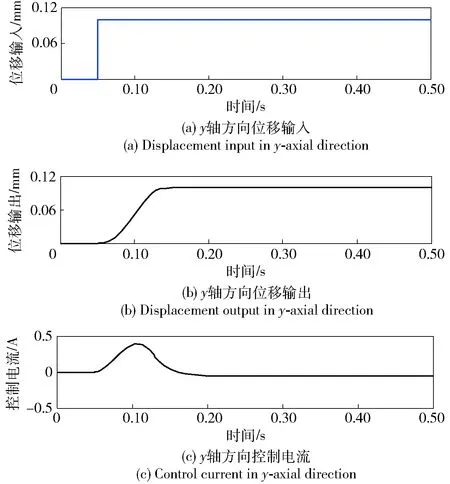
图9 模糊PID控制器y轴方向仿真结果Fig.9 Simulated results of fuzzy PID controller in y-axial direction

根据作动平台参数和LQR控制策略，通过试凑法进行调节，最终得到相对最优控制参数。模糊PID控制器参数kP、kI、kD取值分别为10、22 000、0.01，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6. 模糊PID控制器y轴方向仿真结果如图9所示。0.02 s时，给作动平台y轴方向一个0.10 mm位移阶跃信号，作动平台向上运动，并在0.14 s时稳定。作动平台响应时间为0.12 s，位置最大变化量为0.10 mm，系统无超调。控制电流由0 A到0.40 A再到0 A趋于稳定。与传统PID控制器相比，模糊PID控制器响应时间减少了0.48 s，超调量减少了10%，模糊PID控制器可以使作动平台在y轴方向实现稳定控制，并且对超调量和响应速度的控制效果更好。

4 实验分析

磁力作动器实验装置包括作动平台、控制器dSPACE1103、电涡流位移传感器、E120/06功率放大器。经过反复调试实验装置后，分别对x轴方向、y轴方向平动进行响应特性分析。作动平台控制部件如图10所示。

图10 作动平台控制部件Fig.10 Control components of experimental platform

首先分别给x轴方向2对电磁铁组、y轴方向1对电磁铁组接通1.20 A的偏置电流，使设定值与位移传感器检测数值相等，将经过控制器放大处理后的控制电流与电磁铁组中的偏置电流进行相加、减，构成差动电磁铁组对作动平台进行控制。

4.1 传统PID控制器x轴方向位置响应分析

传统PID控制器参数kP、kI、kD取值分别为2 754、10 000、10时，对作动平台x轴方向平动进行控制。传统PID控制器x轴方向平动位置响应结果如图11所示。

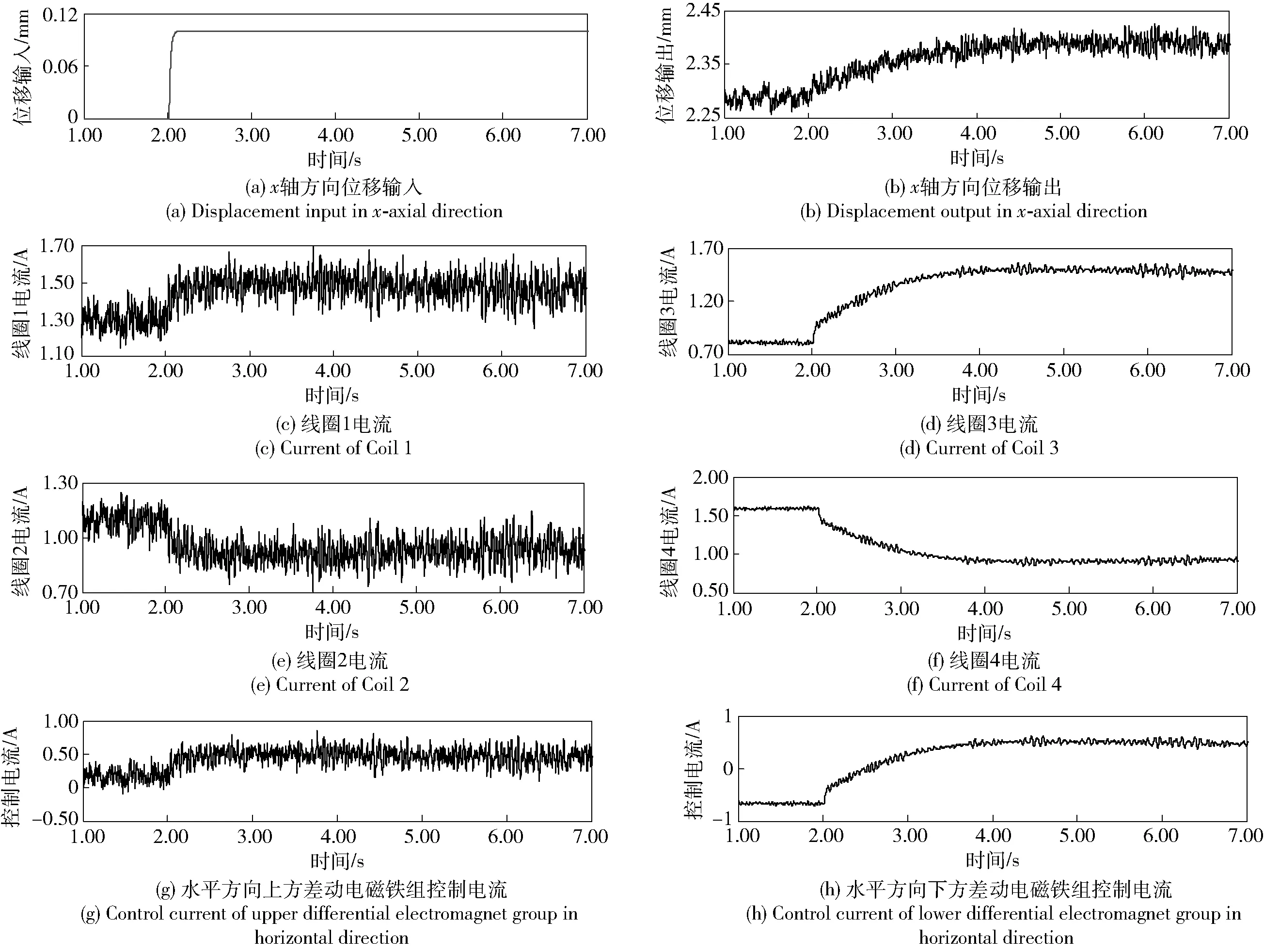
图11 传统PID控制器x轴方向实验结果Fig.11 Experimental results of traditional PID controller in x-axial direction

由图11可见，2.00 s时，给作动平台x轴方向一个0.10 mm位移阶跃信号，作动平台向左运动。作动平台位置响应在4.00 s时趋于稳定，作动平台响应时间为2.00 s，作动平台位置由2.28 mm到2.38 mm，系统无超调。线圈1电流由1.30 A上升到1.50 A，线圈3电流由0.80 A上升到1.50 A，线圈2电流由1.10 A下降到0.85 A，线圈4电流由1.60 A下降到0.90 A，上方差动电磁铁控制电流由0.20 A上升到0.50 A，下方差动电磁铁控制电流由-0.65 A上升到0.50 A. 线圈1、线圈3电流增加，则电磁铁1、电磁铁3电磁力增加；而线圈2、线圈4电流减小，则电磁铁2、电磁铁4电磁力减小。作动平台向左移动，2组差动电磁铁的控制电流变化趋势都是增加的。

4.2 模糊PID控制器x轴方向位置响应分析

模糊PID控制器参数kP、kI、kD取值分别为2 754、10 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6时，对作动平台x轴方向平动进行控制，模糊PID控制器x轴方向平动位置响应结果如图12所示。

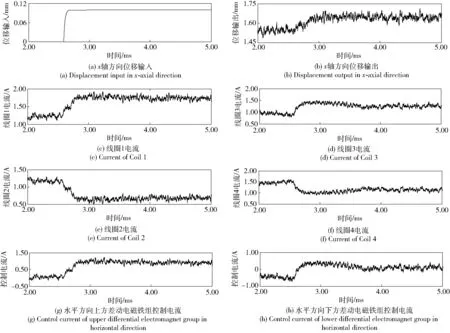
图12 模糊PID控制器x轴方向实验结果Fig.12 Experimental results of fuzzy PID controller in x-axial direction

由图12可见，2.60 s时，给作动平台x轴方向一个0.10 mm位移阶跃信号，作动平台向左移动。作动平台位置响应在3.10 s时逐渐趋于稳定，作动平台响应时间为0.50 s，作动平台位置由1.53 mm到1.63 mm，系统无超调。线圈1电流由1.20 A上升到1.80 A，线圈3电流由1.00 A上升到1.40 A最后稳定在1.30 A，线圈2电流由1.15 A下降到0.65 A，线圈4电流由1.40 A下降到1.00 A最后稳定在1.10 A，上方差动电磁铁控制电流由0 A上升到1.00 A，下方差动电磁铁控制电流由-0.50 A上升到0.40 A最后稳定在0.20 A.线圈1、线圈3电流增加，则电磁铁1、电磁铁3电磁力变大；而线圈2、线圈4电流减小，则电磁铁2、电磁铁4电磁力变小。作动平台向左运动并在3.10 s时稳定，与传统PID控制器对比，模糊PID控制器作动平台位置响应时间减少了1.50 s，响应时间变短，响应速度更快。

4.3 传统PID控制器y轴方向响应特性分析

传统PID控制器参数kP、kI、kD取值分别为10、22 000、0.01时，对作动平台y轴方向进行控制，传统PID控制器y轴方向位置响应结果如图13所示。

由图13可见，1.70 s时，给作动平台y轴方向一个0.10 mm位移阶跃信号，作动平台向上移动。作动平台位移响应在4.00 s时稳定，响应时间为2.30 s，作动平台位置由2.86 mm到2.97 mm，系统无超调。线圈5电流由0.75 A上升到2.20 A，线圈6电流由1.60 A下降到0.35 A，控制电流由-0.70 A上升到1.50 A. 由于控制电流变大，线圈5电流变大，线圈6电流变小，直接导致电磁铁5电磁力变大，电磁铁6电流变小，作动平台上移，最后稳定在新的平衡位置。从中可以看出，传统PID控制器可以使作动平台在y轴方向实现稳定控制。

4.4 模糊PID控制器y轴方向响应特性分析

模糊PID控制器参数kP、kI、kD取值分别为10、22 000、0.01，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6时，对作动平台y轴方向进行控制，如图14所示为模糊PID控制器y轴方向位置响应结果。

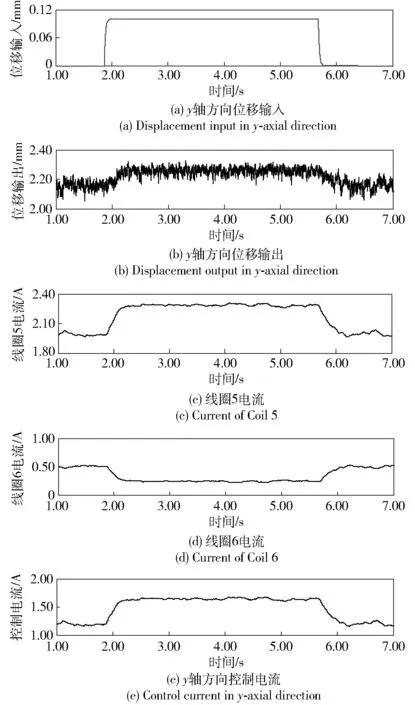
图14 模糊PID控制器y轴方向实验结果Fig.14 Experimental results of fuzzy PID controller in y-axial direction

由图14可见，1.88 s时，给作动平台y轴方向一个0.10 mm位移阶跃信号，作动平台向上运动且响应速度更快，在2.30 s时稳定，其响应时间为0.42 s. 作动平台位置由2.15 mm到2.25 mm，系统无超调。线圈5电流由2.00 A上升到2.30 A，线圈6电流由0.50 A下降到0.25 A，控制电流由1.20 A上升到1.65 A. 与传统PID控制器相比，模糊PID控制器位置响应时间缩短1.88 s，系统无超调。从中可以看出，模糊PID控制器可以使作动平台在y轴方向具有较好位移响应特性，并且控制效果要好于传统PID控制器。

5 模糊PID控制参数优化实验

模糊PID控制器参数kP、kI、kD取值分别为2 754、10 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6时，对作动平台x轴方向平动进行控制。由于x轴方向和y轴方向电磁铁之间耦合和摩擦力的影响，作动平台响应效果不太理想。经过对模糊PID控制器参数反复试凑，当模糊PID控制器参数kP、kI、kD取值分别为15、150 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6时，对作动平台x轴方向平动进行控制，如图15所示为模糊PID控制器x轴方向平动位置响应结果。

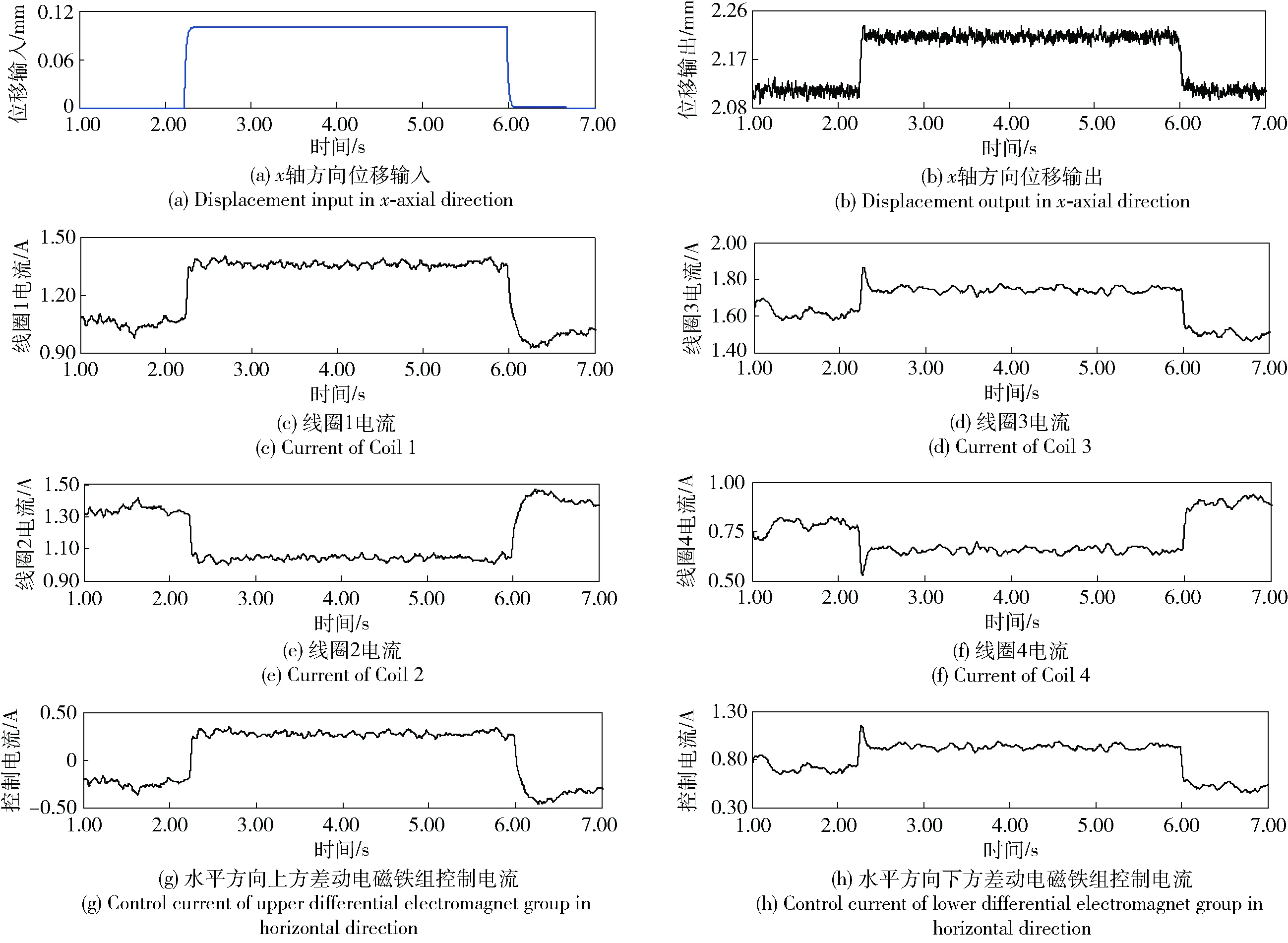
图15 模糊PID控制器参数优化后x轴方向实验结果Fig.15 Experimental results with optimized fuzzy PID controller in x-axial direction

由图15可知，2.25 s时，给作动平台x轴方向一个0.10 mm位移阶跃信号，作动平台位置响应在2.35 s时逐渐趋于稳定，作动平台响应时间为0.10 s. 作动平台位置由2.11 mm到2.21 mm，系统超调为0.9%. 线圈1电流由1.05 A上升到1.35 A，线圈3电流由1.60 A上升到1.85 A最后稳定在1.75 A，线圈2电流由1.30 A下降到1.00 A，线圈4电流由0.75 A下降到0.52 A最后稳定在0.65 A，上方差动电磁铁控制电流由-0.20 A上升到0.30 A，下方差动电磁铁控制电流由0.70 A增加到1.15 A最后稳定在0.95 A. 线圈1、线圈3电流增加，则电磁铁1、电磁铁3电磁力增加；而线圈2、线圈4电流减小，则电磁铁2、电磁铁4电磁力减小。作动平台向左运动并在2.35 s时保持稳定，模糊PID控制器位置响应控制效果较好。

6 结论

1)作动平台在x轴方向位置响应仿真实验中，传统PID控制器和模糊PID控制器二者控制效果基本相同。作动平台在y轴方向位置响应仿真实验中，模糊PID控制器响应时间较传统PID控制器响应时间缩短0.48 s，超调量减少10%.

2)x轴方向模糊PID控制器参数kP、kI、kD取值分别为2 754、10 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6；y轴方向模糊PID控制器参数kP、kI、kD取值分别为10、22 000、0.01，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6. 该情况下的位置响应实验结果说明，与传统PID控制器相比，模糊PID控制器x轴方向位置响应时间提高了1.50 s，在y轴方向位置响应时间缩短了1.88 s. 在切割速度低、精度要求不高的低速切割中，可用此模糊PID控制器参数进行切割。

3)模糊PID控制器参数kP、kI、kD取值分别为15、150 000、10，量化因子取值分别为2、0.01，比例因子取值分别为5、20、0.000 6情况下，x轴方向优化实验中，作动平台响应时间提高到0.10 s，此优化参数可用于切割速度快、精度要求高的高速切割。