基于排队论的中硬围岩长大隧道施工机群优化配置方法

曹豪荣，彭立敏，杜昆，雷明锋, 2，刘瑶



基于排队论的中硬围岩长大隧道施工机群优化配置方法

曹豪荣1，彭立敏1，杜昆1，雷明锋1, 2，刘瑶1

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

针对隧道施工过程中各作业线内部产生的机械排队作业现象，采用随机过程排队论方法以Ⅲ级围岩为例研究中硬围岩长大隧道施工循环作业线中机械配套问题，提出顾客为有限源的M/M/1/m/m排队系统的求解方法，由此得到基于快速施工的最优机械配套方案。结合黄岩隧道妹子娘冲斜井段的工程实例，得到Ⅲ级围岩下出碴运输系统以及锚喷支护系统的最优配置，可为工程实际施工提供一定参考。

隧道施工；排队系统；快速施工；机械配套；最优配置

在隧道施工过程中，各作业线内部都会产生机械排队问题。以出碴运输作业线和锚喷支护作业线为例，在这2条作业线中，由挖掘机与装载机组成的掌子面出碴机组、车载式湿喷机组作为服务台，自卸汽车运碴、混凝土运输车作为接受服务的顾客。若顾客偏少，服务台长时间处于闲置状态，影响施工效率；若顾客偏多，又会出现在服务台排队的现象，即自卸汽车、混凝土运输车运力过剩而装载机、车载式湿喷机效率不足，这样又会导致台班费的无故增加。因此，如何确定挖掘机、装载机与自卸汽车和车载式湿喷机与混凝土运输车的组合方案显得尤为重要。上述产生的排队问题，其最有效的解决方案是利用随机过程理论中的排队论。排队理论，是研究系统的随机聚散现象、随机服务系统工作过程的数学理论及其方法，又叫做随机服务系统理论[1]。排队理论越来越得到国内外学者的重视，LU等[2−3]基于排队理论对公共医疗资源合理分配进行研究与探讨；Haghighinejad等[4]应用排队理论和仿真模型对急救中心服务进行最优化，从而减少了患者的等待时间；WANG等[5]采用M/M/c模型对银行客户排队服务进行模拟，并得到最优解；XIONG等[6]基于排队理论对虹桥交通枢纽旅客信息服务模式进行研究与设计；Iyer[7]利用排队理论对运输服务效率进行研究，并进一步提高了运输能力；Naima等[8]基于排队理论对交通拥挤现象展开分析，并提出相应的最优解决方案；李波[9]基于排队论对地铁服务效率进行最优化研究；PENG等[10]应用排队理论对综合铁路客运枢纽城市交通疏散系统进行疏散效率优化研究。排队论在生活中的应用非常广泛，针对隧道施工过程中排队问题也最好采用排队理论进行解决。显然，在出碴运输作业线中，最理想的工作状态是：当一辆自卸汽车在服务台被装满离开的同时，下一辆自卸汽车刚好到达服务台开始接受服务。容易得知，服务台的服务效率与顾客的到达率是对该系统至关重要的2个因素。通过排队论解决作业线内部各工序间机群配套作业方案时，首先要研究的问题是单工序机械设备的单机作业特性[11−13]。

1 中硬围岩全断面施工流程

以Ⅲ级围岩为例，中硬围岩隧道单循环进尺的关键工序作业流程如下。

1) 测量放线。

2) 凿岩台车根据钻爆眼位设计图在掌子面进行钻孔，而后进行人工装药爆破，降尘及清危后开始出碴运输作业线。

3) 出碴运输作业线由挖掘机、装载机及自卸汽车组成。挖掘机与装载机构成服务体系服务台，自卸汽车在服务台接受服务后将石碴运至弃碴场，空车返回工作面，完成一次运输循环。

4) 锚喷支护作业线由车载式湿喷机与混凝土运输车组成。湿喷机作为服务体系服务台，混凝土运输车在服务台接受服务(将混凝土装料到湿喷机中)返回拌料场，装料后又运输至工作面，完成一次运料循环。

5) 湿喷机作业完成后，结束锚喷支护作业线。从凿岩台车开始工作至初期支护结束便完成了一次中硬围岩(以Ⅲ级围岩为例)Ⅲ级围岩单循环 进尺。

作业流程如图1所示。

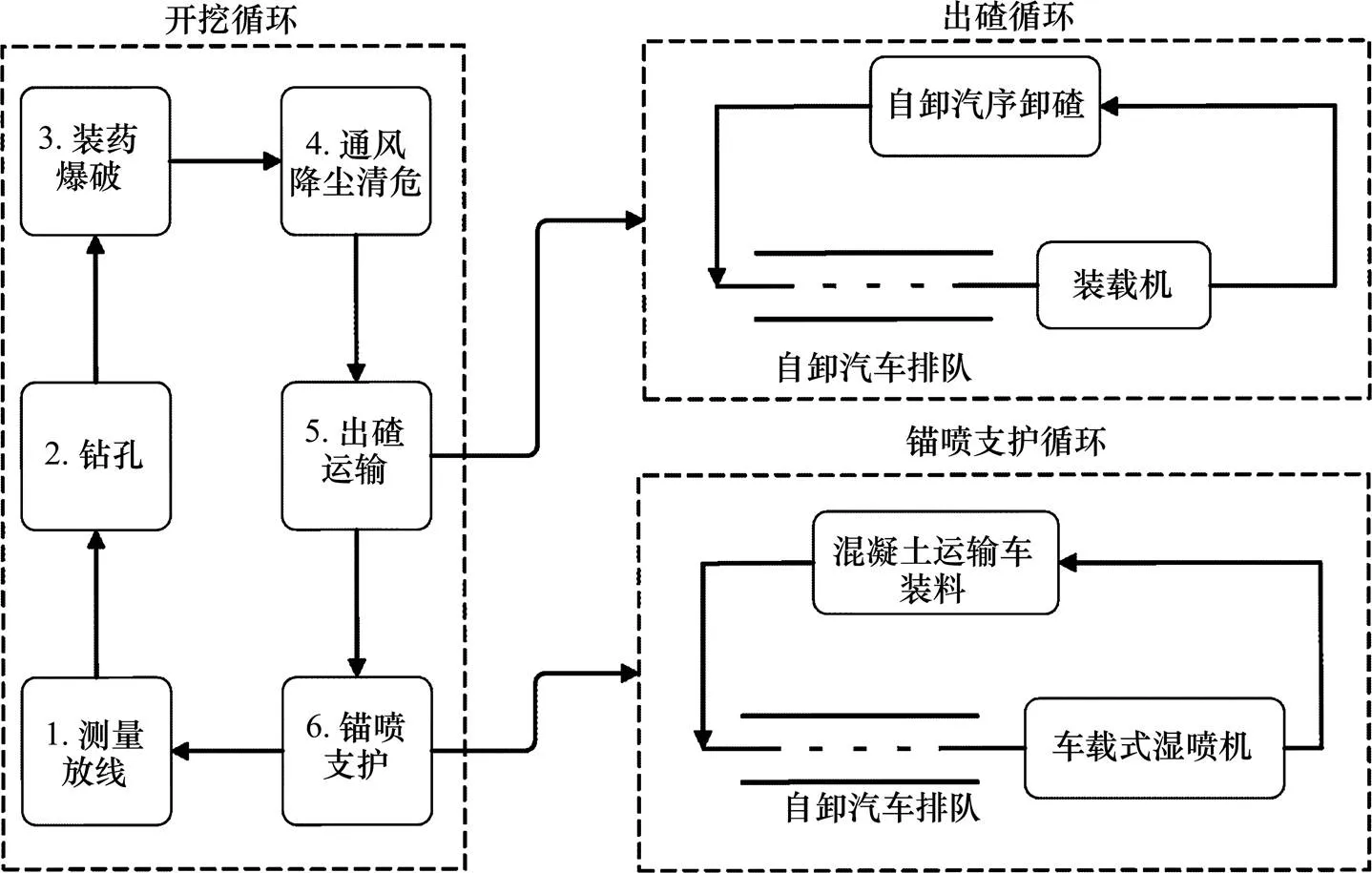
图1 Ⅲ级围岩单循环进尺机群作业流程图

2 顾客为有限源的M/M/1/m/m型排队系统

排队系统的基本要素有：输入过程、排队规则和服务机构[14−15]。

1) 输入过程：输入过程是指顾客到达排队系统的规律。一般来说，到达排队系统的规律与不同机械的单机运行规律和作业特性相关，根据现场的试验研究容易得到在出碴运输作业线与锚喷支护作业线中，顾客间相互独立，均以负指数分布的时间间隔到达排队系统。

2) 排队规则：排队规则指的是排队顾客接受服务的顺序，即为先到先服务制度(FCFS：First Come First Service)。

3) 服务机构：指的是服务台的数量、串并联关系以及服务时间规律，且装载机与车载式湿喷机均以负指数分布的时间间隔进行服务。

为对不同排队系统加以区分描述，用“Kendall记号”对排队系统进行命名，其固定格式：A/B/C/D/ E/F，其中，A为顾客进入排队系统时间间隔概率分布；B为服务时间概率分布；C为服务台个数；D为排队系统中顾客容量限额；E为顾客源限额；F为排队规则(省略则默认为FCFS型)。

故M/M/1/m/m型排队系统即为：顾客源为限额，到达时间间隔按负指数分布，服务台服务时间间隔按负指数分布的排队系统，如图2。

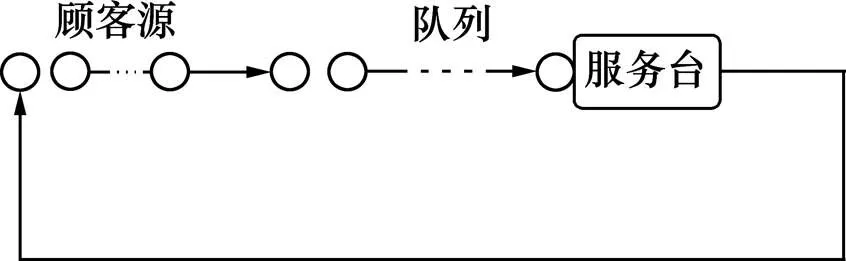
图2 M/M/1/m/m型排队系统

记以下常用符号：s为平均队长(排队顾客与接受服务顾客数量之和)；q为平均排队长(排队顾客数量)；s为平均逗留时间(排队时间与接受服务时间之和)；q为平均等待时间(排队时间)；为顾客平均到达率；1/为顾客平均到达时间间隔；为平均服务率；1/为平均服务时间；P为系统中有个顾客的概率。

在该排队系统中，顾客平均到达率为，而顾客源为，那么在系统外的顾客平均数为−s，所以系统的有效到达率为：e=(−s)考虑排队系统稳定后，达到“输入”=“输出”状态，可得到如下关于P状态的差分方程：

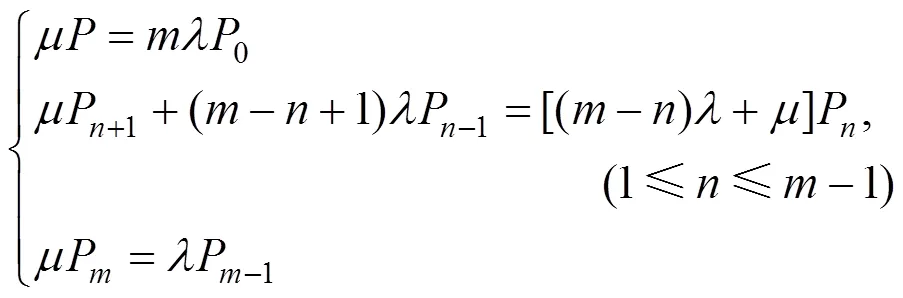
求解上述差分方程得：

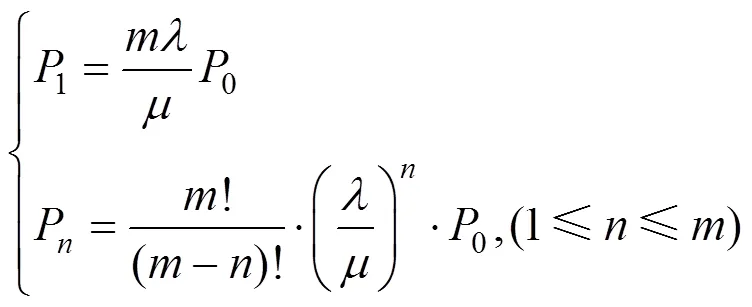
其中：

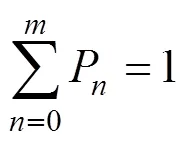
将式(2)与式(3)联立可得：

即：

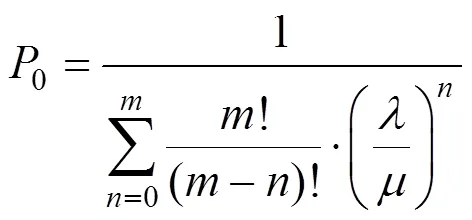
进而求得排队系统的主要绩效指标：

1) 平均队长期望值s：

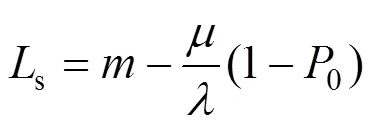
2) 平均排队长期望值q：

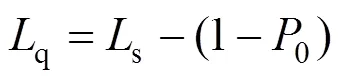
3) 顾客平均逗留时间期望值s：

4) 顾客平均等待时间期望值W：

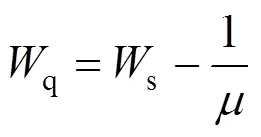
5) 系统有效到达率e：

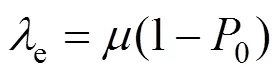
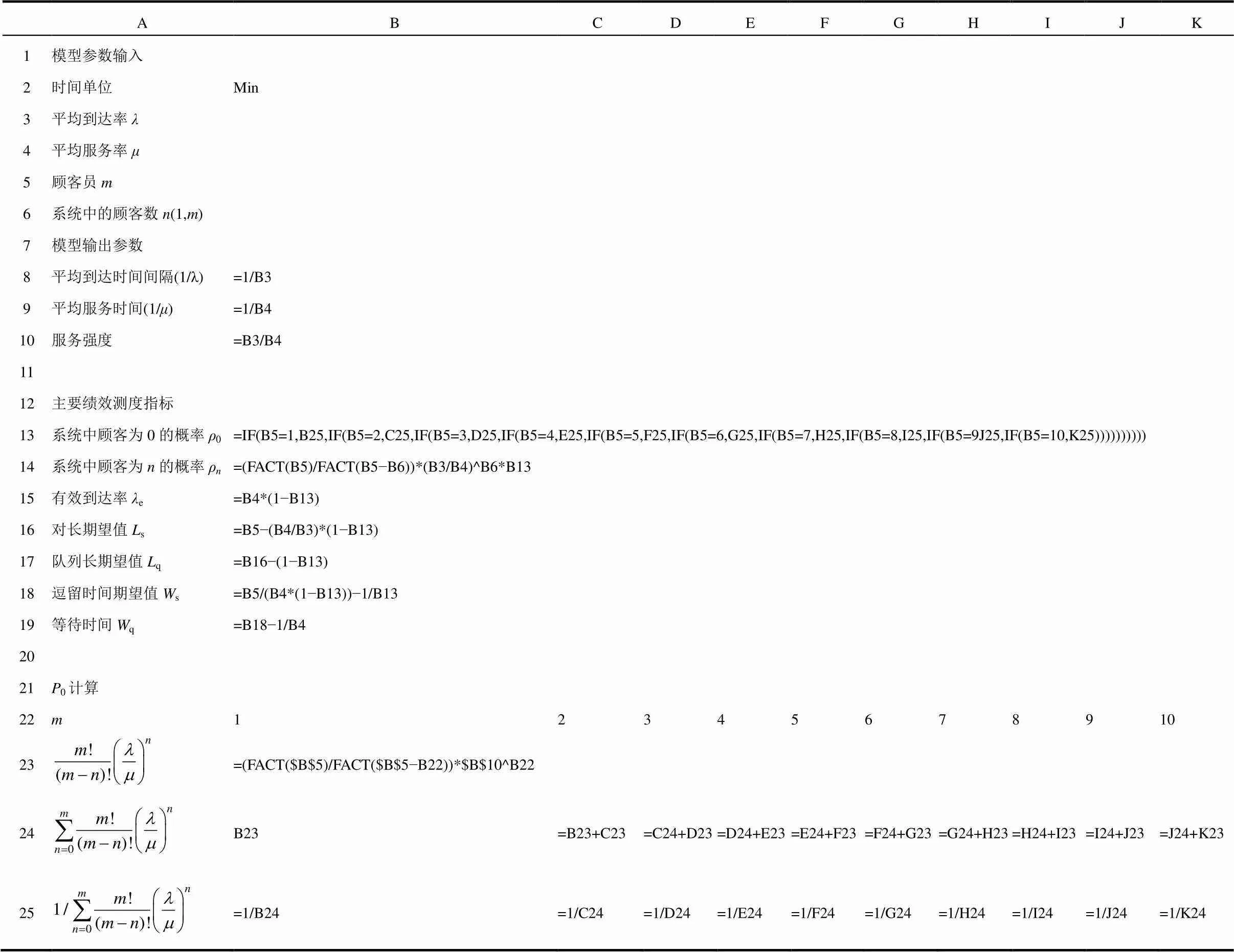
利用Microsoft Excel编制M/M/1/m/m型排队系统求解器，见图3。

ABCDEFGHIJK 1模型参数输入 2时间单位Min 3平均到达率λ 4平均服务率μ 5顾客员m 6系统中的顾客数n(1,m) 7模型输出参数 8平均到达时间间隔(1/λ)=1/B3 9平均服务时间(1/μ)=1/B4 10服务强度=B3/B4 11 12主要绩效测度指标 13系统中顾客为0的概率ρ0=IF(B5=1,B25,IF(B5=2,C25,IF(B5=3,D25,IF(B5=4,E25,IF(B5=5,F25,IF(B5=6,G25,IF(B5=7,H25,IF(B5=8,I25,IF(B5=9J25,IF(B5=10,K25)))))))))) 14系统中顾客为n的概率ρn=(FACT(B5)/FACT(B5−B6))*(B3/B4)^B6*B13 15有效到达率λe=B4*(1−B13) 16对长期望值Ls=B5−(B4/B3)*(1−B13) 17队列长期望值Lq=B16−(1−B13) 18逗留时间期望值Ws=B5/(B4*(1−B13))−1/B13 19等待时间Wq=B18−1/B4 20 21P0计算 22m12345678910 23=(FACT($B$5)/FACT($B$5−B22))*$B$10^B22 24B23=B23+C23=C24+D23=D24+E23=E24+F23=F24+G23=G24+H23=H24+I23=I24+J23=J24+K23 25=1/B24=1/C24=1/D24=1/E24=1/F24=1/G24=1/H24=1/I24=1/J24=1/K24

图3 M/M/1/m/m模型算法

Fig. 3 Arithmetic of M/M/1/m/m model

3 案例分析

以黄岩隧道妹子娘冲斜井段为例，对出碴运输与锚喷支护作业线分别进行机群优化配置。

3.1 出碴运输作业线机群状态分析

在出碴运输作业线中，自卸汽车在卸碴场卸碴不存在排队现象，即自卸汽车抵达卸碴场便可以卸碴。其排队系统如图4。

装载机装碴时间服从负指数分布，每装一车碴平均耗时4.3 min；自卸汽车到达排队系统时间间隔服从负指数分布，每循环时间耗时30 min，据此可得到该排队系统的输入参数：=1/30，=1/4.3，=/=0.143 3。

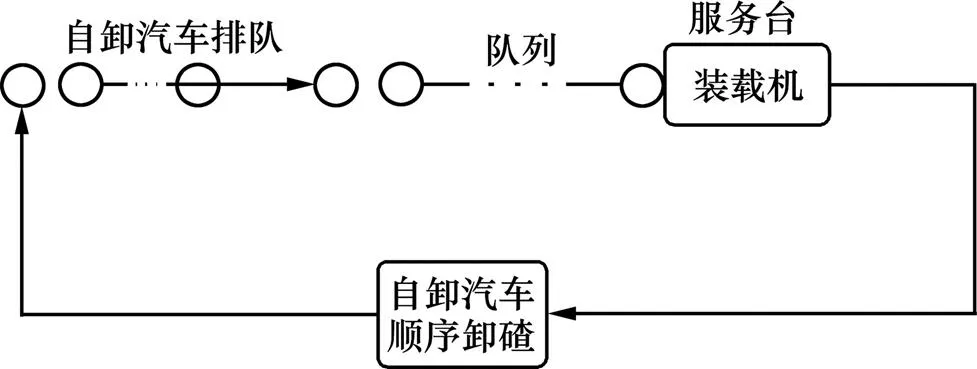
图4 出碴运输作业线循环系统

在该工作面现场施工中，自卸汽车数量为7台，服务台空闲等待时间为105 min。为寻求最佳配置方案，在Excel求解器中输入模型参数，令=5，6，7，8，9和10。排队系统主要绩效测度指标见表1。分析可见：

1) 当自卸汽车数量为7台时，0为0.329，即装载机有0.329的概率处于闲置状态，现场实测装载机闲置时间为105 min，对施工进度影响较大。

2) 若配置自卸汽车数量由7台增至8台时，顾客等待时间q有所降低，而从8台增至9台时，顾客等待时间q又有所回升。其非一致性变化表明，当自卸汽车数量少于7台时，数量偏少，不能满足运力要求，到达工作面时间很不均匀，在某段时间几辆车同时到达，使得服务台处于满载状态，在其他时间又没有一辆车到达，使得服务台闲置；而当自卸汽车数量增加至8台及以上时，运力逐渐满足要求，自卸汽车到达工作面时间较为均匀。

3) 当自卸汽车数量为10台时，装载机仅有0.084的概率处于闲置状态，出碴运输循环衔接紧密，同时自卸汽车平均等待时间为12.633 min，相较于7台车的10.544 min增加幅度不大。

4) 自卸汽车数量选用10台。相较于现场7台自卸汽车的配置，效率提升24.5%。

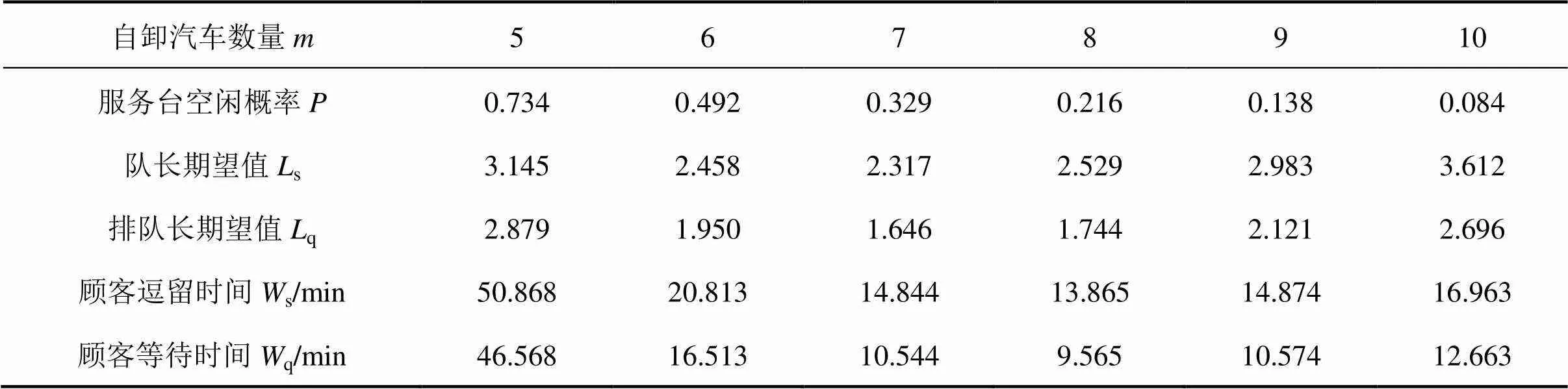
表1 不同自卸汽车数量配置的排队系统绩效测度表

3.2 锚喷支护作业线机群状态分析

在锚喷支护作业线中，混凝土运输车在混凝土搅拌站装料不存在排队现象，即混凝土搅拌站供料能力充足，混凝土运输车到达后便可装料。其排队系统如图5。

图5 锚喷支护作业线循环系统

车载式湿喷机喷射每车混凝土时间服从负指数分布，每喷一车平均耗时33.5 min；混凝土运输车到达排队系统时间间隔服从负指数分布，每循环时间耗时87.5 min，据此可得到该排队系统的输入参数：=1/87.5，=1/33.5，=0.383。

在该工作面现场施工中，混凝土运输车数量为3台，单循环进尺工序耗时中服务台空闲等待时间为115 min。为寻求最佳配置方案，在Excel求解器中输入模型参数，令=3，4，5，6，7和8。排队系统主要绩效测度指标见表2。从中可见：

1) 当混凝土运输车数量由3台增至4台时，顾客等待时间q有所降低，而从4台增至5台时，顾客等待时间q又有所回升。其非一致性变化表明，当混凝土运输车数量为3台时，数量偏少，运力不足，到达工作面时间很不均匀，在某段时间几辆车同时到达，使得服务台处于满载状态，在其他时间又没有一辆车到达，使得服务台闲置；而当自卸汽车数量增加至4台及以上时，运力逐渐满足要求，自卸汽车到达工作面时间较为均匀。

2) 当混凝土运输车数量为4台时，虽然排队长期望值q为1.089，满足理想工序衔接情况，即一辆车在接受服务的同时只有一辆车在排队等待。但服务台仍有0.194的概率处于闲置状态，基于快速施工目标考虑，该闲置概率仍然偏高。

3) 当混凝土运输车数量增至5台及以上时，服务台闲置概率已低于0.1，同时5台车的排队长期望值q为1.695，平均等待时间q为62.040 min，相较于3台车是0.915的排队长和53.139的平均等待时间来讲略有提高，但处于可接受水平。

4) 混凝土运输车数量选用5台，相较于现场3台混凝土运输车的配置，效率提升33.8%。

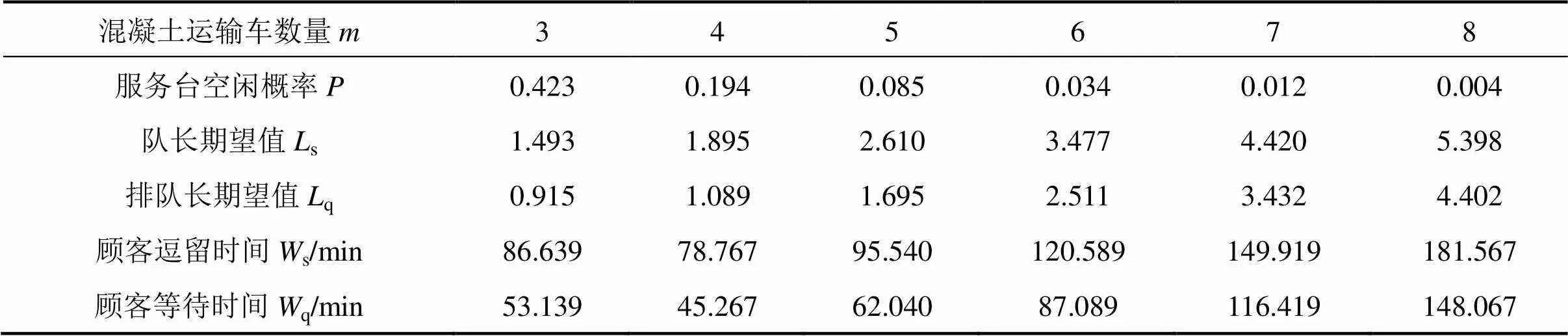
表2 不同混凝土运输车数量配置的排队系统绩效测度表

3.3 工程机械化配套方案评价

经过以上黄岩隧道机械选型评定与机群施工模式分析可以看出：

1) 该工程机械设备选型情况合理，属于在给定影响因素下的最优方案选择。现场施工机械化程度极高，相较于传统隧道施工方案，施工进度和施工成本都有了很大的改善。

2) 现场循环进尺机械配套数量略有不妥，有待改进。应加强各工序间的衔接以便实现快速施工的需求。

3) 随着工程的不断进展，排队系统中的相对参数应加以相应调整，机械配套方案也要作出相适应的改变。

4 结论

1) 基于随机过程排队论方法，研究提出顾客为有限源排队系统的求解方法，得到隧道Ⅲ级围岩段快速施工的最优机械配套方案。

2) 依托黄岩隧道妹子娘冲斜井段工程进行实例分析，获得该隧道Ⅲ级围岩段快速施工机群配套方案：1台挖掘机+1台装载机+10台自卸汽车；锚喷支护系统最优配置为：1台车载式湿喷机+5台混凝土运输车。

[1] 齐文雪. 排队理论及其应用[D]. 济南: 山东大学, 2016. QI Wenxue. Queuing theory and it’s application[D]. Jinan: Shandong University, 2016.

[2] LU Xiaoqing, TIAN Ruyu, GUAN Shuming. Medical equipment utility analysis based on queuing theory[J]. Journal of Computers, 2012, 7(9): 2232−2239.

[3] Appa Iyer S. Application of queuing theory in health care: a literature review[J]. Operations Research for Health Care, 2013, 2(1): 25−39.

[4] Haghighinejad Hourvash Akbazi, Kharazmi Erfan, Hatam Nahid, et al. Using queuing theory and simulation modelling to reduce waiting times in an Iranian emergency department[J]. International Journal of Community Based Nursing and Midwifery, 2016, 4(1): 11−26.

[5] WANG Yubo, CHENG Qian, CAO Jinde. Optimized M/M/c model and simulation for bank queuing system[C]// 2010 IEEE International Conference on Software Engineering and Service Sciences (ICSESS), 2010: 474−477.

[6] XIONG Honglin, FAN Chongjun. Research and design on passengers traffic information services mode of Hongqiao transport hub[J]. International Journal of Business and Management, 2010, 5(4): 194−199.

[7] Iyer Ranganath K. Creating additional capacity by applying queuing theory to transportation services[J]. IIE Annual Conference Proceedings, 2013: 1−32.

[8] Naima Saeed, Odd I Larsen. Application of queuing methodology to analyze congestion: a case study of the manila international container terminal, philippines[J]. Case Studies on Transport Policy, 2016, 4(2): 143−149.

[9] 李波. 基于排队论的地铁站服务效率优化研究[D]. 武汉: 华中科技大学, 2016. LI Bo. Research on service efficiency optimization of subway station based on queuing theory[D]. Wuhan: Huazhong University of Science and Technology, 2016.

[10] PENG B, YUN L. Urban traffic evacuation system for comprehensive railway passenger transport hub and its evacuation efficiency optimization Research[J]. Applied Mechanics & Materials, 2012, 209: 771−774.

[11] 孙高磊. 道路施工机群资源配置和计划调度沥青混凝土路面机械化施工系统状态分析与技术经济评价研究[D]. 重庆: 重庆交通大学, 2003. SUN Gaolei. Resource allocation and planning and scheduling of road construction machinery cluster analysis and technical and economic evaluation on mechanized construction system of asphalt concrete pavement[D]. Chongqing: Chongqing Jiaotong University, 2003.

[12] 李鹏伟. 基于多臂凿岩台车和湿喷机组的公路隧道施工机械化作业模式研究[D]. 重庆: 重庆交通大学, 2014. LI Pengwei. Analysis on mechanized working-mode of highway tunnel construction based on computer- controlled drilling jumbo and large wet-spraying unit[D]. Chongqing: Chongqing Jiaotong University, 2014.

[13] 欧阳结新. 公路隧道洞身开挖与支护的多机种机械化作业模式与集成研究[D]. 重庆: 重庆交通大学, 2015. OUYANG Jiexin. Research on the heterogenous mechanized working-mode and integration of highway tunnel excavation and supporting of holes[D]. Chongqing: Chongqing Jiaotong University, 2015.

[14] 黄德中. 土方工程机械选型配套的排队论网络分析[J]. 农业机械学报, 2004, 35(3): 79−82. HUANG Dezhong. Queuing analysis for selection of construction machinery[J]. Transactions of the Chinese Society of Agricultural Machinery, 2004, 35(3): 79−82.

[15] 黄德中. 工程机械选型配套的排队论网络[J]. 起重运输机械, 2003(5): 35−37. HUANG Dezhong. Queuing theory network for selection and matching of engineering machinery[J]. Hoisting and Conveying Machinery, 2003(5): 35−37.

Optimal allocation of long tunnel construction machinery groups in middle hard surrounding rock based on queuing theory

CAO Haorong1, PENG Limin1, DU Kun1, LEI Mingfeng1, 2, LIU Yao1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. Key Laboratory of Engineering Structure of Heavy Haul Railway (Central South University), Changsha 410075, China)

Aimed at the mechanical queuing phenomenon produced within the each working line of tunnel during long tunnel construction, and the problem of mechanical matching in the loop operation line was studied based on the queuing theory of the stochastic process theory by taking grade III wall rock as a example. A method for solving the M/M/1/m/m queuing system with limited sources was proposed. Then, the optimal mechanical matching scheme based on rapid construction was obtained. Finally, combined with the engineering example of the Huangyan tunnel, the optimum configuration of the mucking and transporting system and the bolting and shotcrete supporting system under grade III wall rock was obtained, and it can provide some reference for the actual construction of the project.

tunneling; queuing system; rapid construction; mechanical matching; optimal allocation

10.19713/j.cnki.43−1423/u.2019.02.033

TU745.3

A

1672 − 7029(2019)02 − 0535 − 07

2018−02−01

国家自然科学基金资助项目(51508575, U1734208)；中建股份科研项目(CSCEC-2016-Z-21-1)

雷明锋(1982−)，男，湖南祁东人，副教授，博士，从事隧道与地下工程方面的教学与科研工作；E−mail：mingdfenglei@csu.edu.cn

(编辑 阳丽霞)