变截面薄壁箱梁剪力滞计算的板元梁段法
2019-03-07李林安耿文宾刘习军张庆周聪
李林安,耿文宾,刘习军,张庆,周聪
变截面薄壁箱梁剪力滞计算的板元梁段法
李林安1, 2,耿文宾1,刘习军1, 2,张庆1,周聪1
(1. 天津大学 机械工程学院,天津 300350;2. 天津市现代工程力学重点实验室,天津 300350)
为了计算分析变截面薄壁箱梁剪力滞效应及其参数的敏感性,提出一种考虑剪力滞效应的三节点板元梁段法。基于箱梁截面内应变-位移-基本变形之间的关系,以形函数作为单元内高度变化的插值函数,利用最小势能原理推导出梁段法对应的等参有限元行列式。使用编写的有限元程序对算例进行计算,梁段单元法计算结果与模型的实测值及有限元数值结果均吻合良好,验证了理论方法与公式推导的正确性和可靠性;在集中和均布荷载2种工况下,分别考察变截面薄壁箱梁剪力滞效应分析中常见影响参数的敏感性,研究结果表明:翼宽比、宽跨比和腹板倾角是影响变截面箱梁剪力滞效应的主要因素。文中方法计算精度好、效率高,对分析变截面箱梁的剪力滞效应具有一定的参考价值。
变截面;薄壁箱梁;剪力滞效应;参数敏感性;等参有限元
为满足路线设计和跨越地形地物的需要,具有良好结构性能和受力特性的变截面连续箱梁在桥梁上部结构设计中被广泛采用[1]。工程中因剪力滞效应引起的一系列安全隐患备受工程师的关 注[2−3],但分析变截面连续箱梁桥的剪力滞效应,不能直接采用等截面箱梁剪力滞效应的计算公式。因此,研究适用于变截面连续箱梁剪力滞效应分析的方法是必要的。目前,关于变截面箱梁剪力滞问题的研究已有一定的进展。CHANG等[4−5]较早利用有限差分法研究了变截面悬臂箱梁和变截面组合箱梁的剪力滞效应;刘世忠等[6]以能量变分法为基础,建立了考虑变截面箱梁剪力滞和剪切变形双重效应的有限元列式;罗旗帜等[7−9]将基于能量变分法推导的剪力滞控制微分方程的齐次解作为梁段的位移模式,建立了变截面箱梁剪力滞分析的有限段法;何志刚等[10]采用能量变分法推导了考虑截面配筋后的剪力滞控制微分方程,研究了变截面悬臂箱梁截面配筋对剪力滞效应的影响;韦成龙等[11]提出一种分析变截面连续箱梁桥剪力滞及剪切变形双重效应的传递矩阵法;丁南宏等[12−13]基于等效刚度法提出了一种变截面悬臂箱梁剪力滞效应的近似计算方法。变截面箱梁因存在高度变化的现象,所以考虑剪力滞效应的控制微分方程很难得出解析解[7],其往往需要借助有限元法进行分析,但有限元法分析变截面箱梁剪力滞效应存在操作繁杂和自由度较多的问题。因此为计算分析变截面薄壁箱梁剪力滞效应和提高计算效率,本文提出一种考虑剪力滞效应的三节点板元梁段[14−15],通过建立箱梁各翼板关于基本变形的空间位移表达式,确定箱梁截面内应变−位移−变形模式之间的关系,基于最小势能原理建立梁段法对应的等参有限元行列式。算例的理论计算结果与已有实测值及数值结果均吻合良好,从而验证了理论方法与公式推导的正确性和适用性。
1 坐标系及基本假定
如图1所示,在竖直对称的变截面梯形箱梁段上,建立笛卡尔坐标系(,,),坐标系中箭头所指方向为坐标轴正方向,为箱梁闭合截面壁厚中心线的方向。箱梁横截面顶板、底板和悬臂板的宽度分别表示为b,b和b,相应的厚度分别表示为1,2和3,y和y依次为箱梁截面形心和扭转中心的竖向坐标,(z)为截面处箱梁的高度,以及h和h分别为形心轴距顶板、底板中心线的距离。
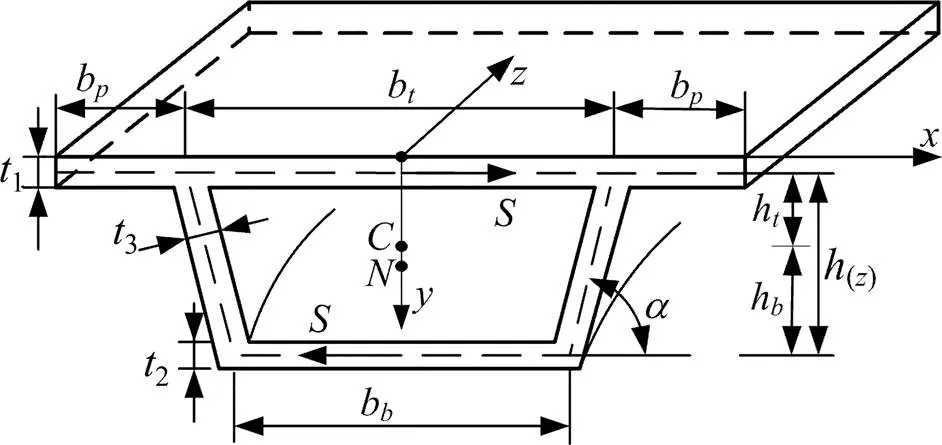
图1 坐标系及几何参数
在线弹性理论基础上引入以下假设:计入挠曲剪应变对弹性应变能的影响;翼板因扭转翘曲引起的正应力和剪应力沿壁厚方向均匀分布;横截面上翘曲纵向位移沿箱梁截面的分布规律与自由扭转时的纵向位移相同,引入独立的扭转翘曲位移变量;在竖向弯曲中计入剪力滞后效应,但不考虑畸变的影响。
2 箱梁内任意点的位移和应变
2.1 基本变形和空间位移
图2为截面变形所考虑的8种基本变形模式,结合截面形心和扭心的位移参数可构造变截面箱梁截面内任意点(,,)处的空间位移表达式:
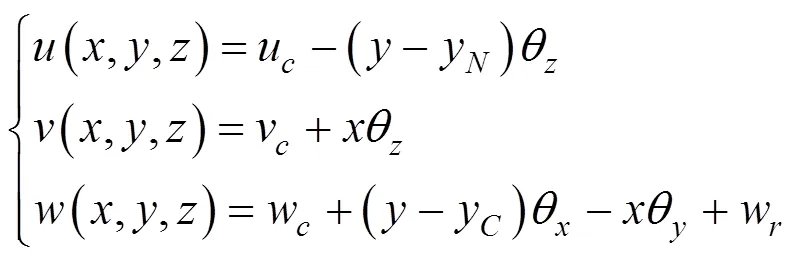
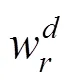
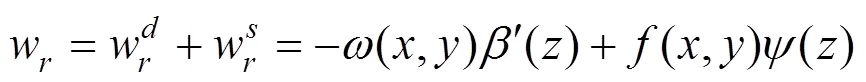
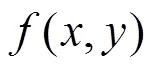
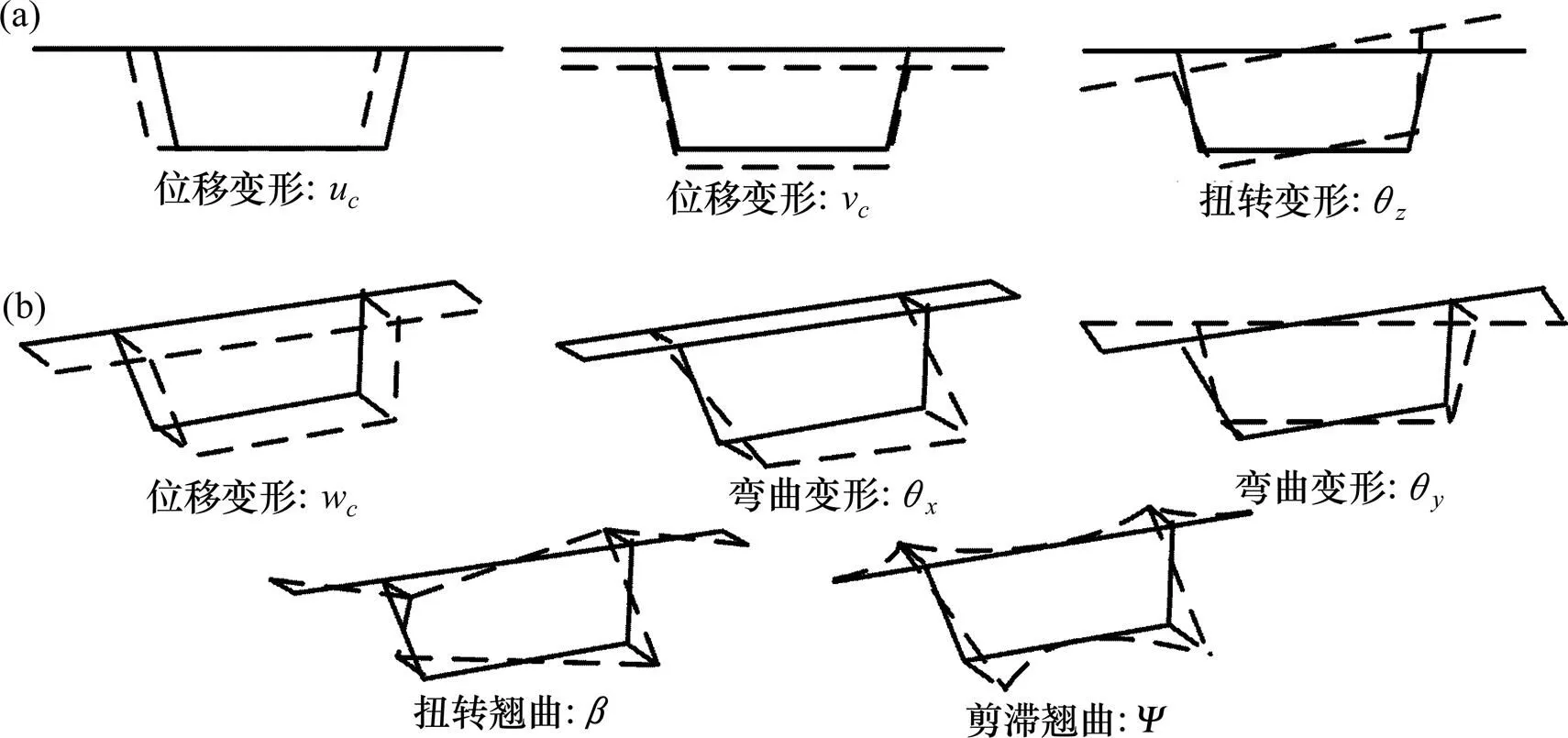
(a) 截面内;(b) 截面外
2.2 应变和位移关系
箱梁截面上任意点的正应变和剪应变与空间位移场函数的关系为
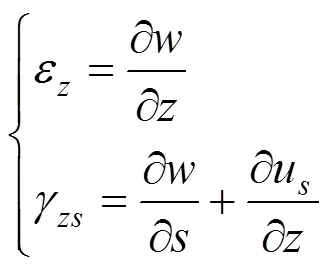
其中:u是闭合截面内任意点沿方向的位移,各翼板u的具体表达式参考文献[14]。
因变截面箱梁中高度为变量,所以位移表达式中y,y,和均为关于的变量。箱梁内任意点正向应变与基本变形模式之间的关系为
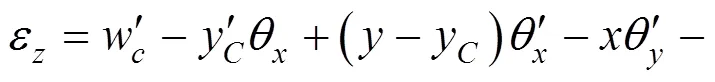
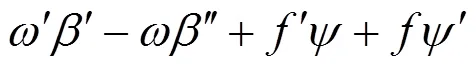
各翼板的剪应变为
顶板:
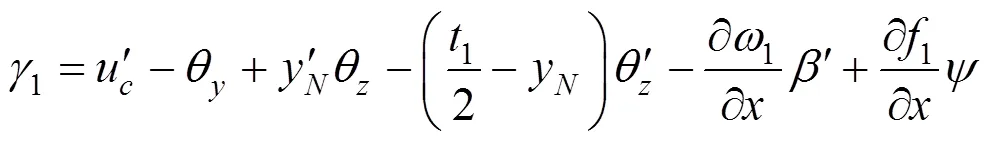
右腹板:
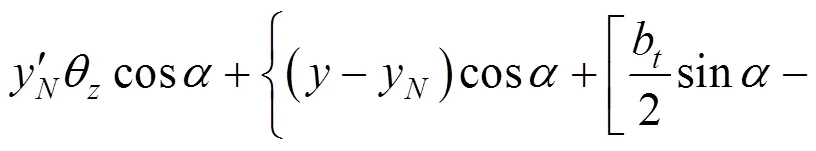
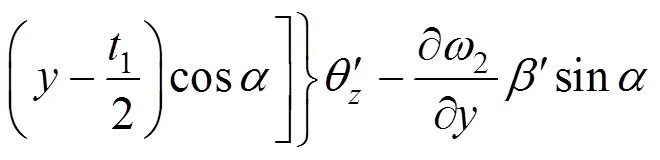
底板:
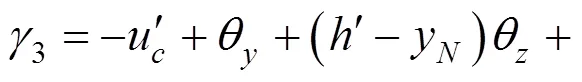
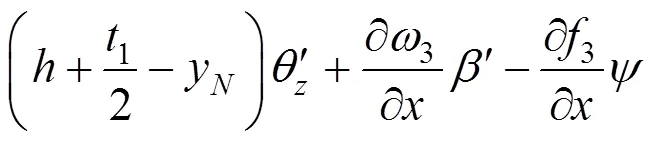
左腹板:
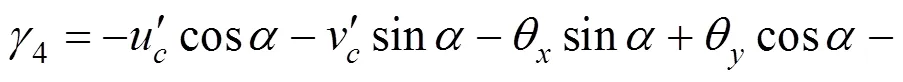
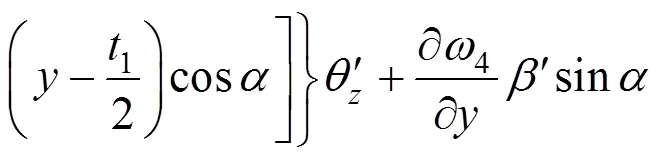
3 有限单元列式
3.1 几何单元及形函数
位移场函数中包含8种基本变形模式,即单元上每个节点具有8个自由度,因梁段采用三节点的一维等参单元,所以单元的基本变形列阵为
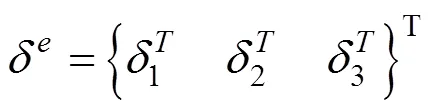
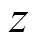
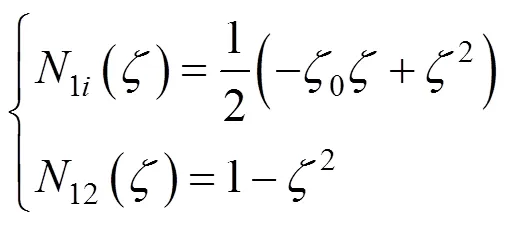
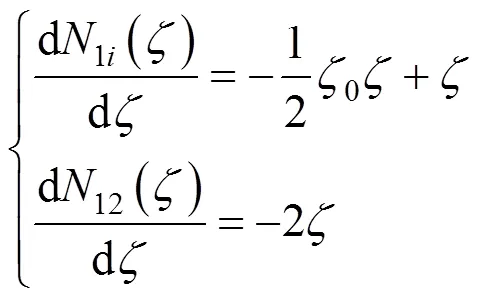
式中:=1时,0=1;=3时,0=−1。
0形函数作为单元坐标和截面高度变量(z)的插值形函数,即
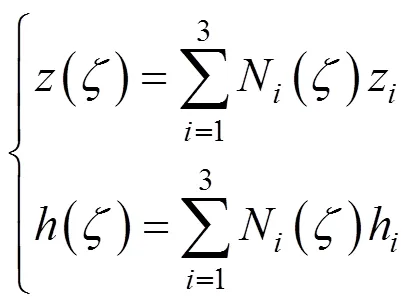
为建立广义局部坐标和整体坐标内导数之间的变换关系,引入雅克比系数:
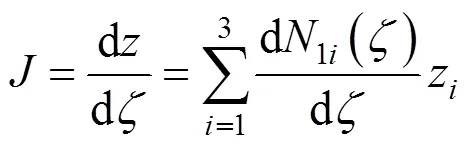
3.2 单元应变矩阵
单元内任意截面上的基本位移变量由构造的形函数与节点基本位移表示为
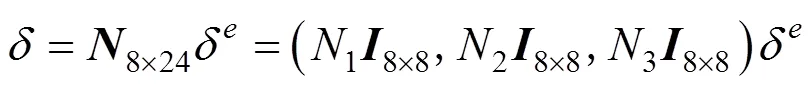
图3 形函数
Fig. 3 Shape Functions
单元内截面上任意点正应变和剪应变为
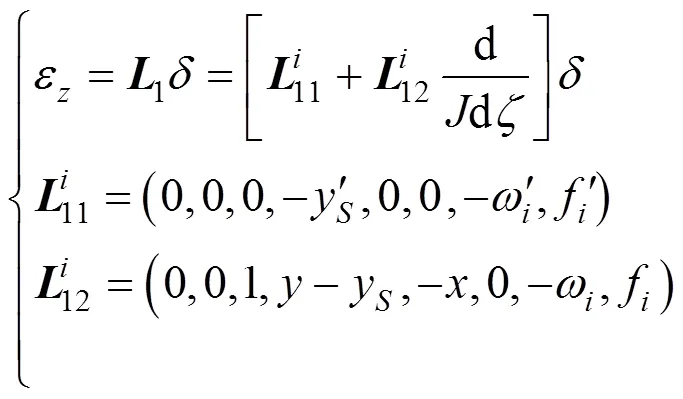
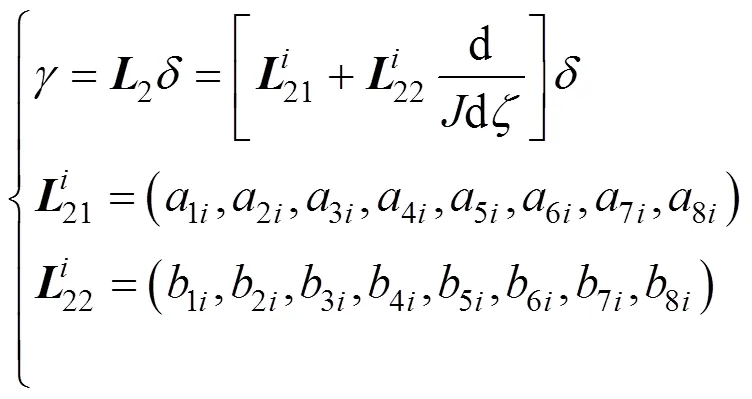
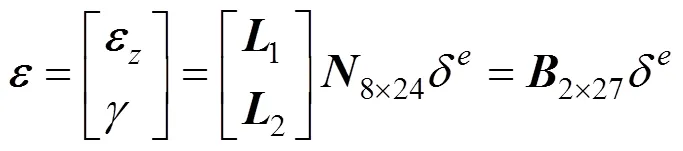
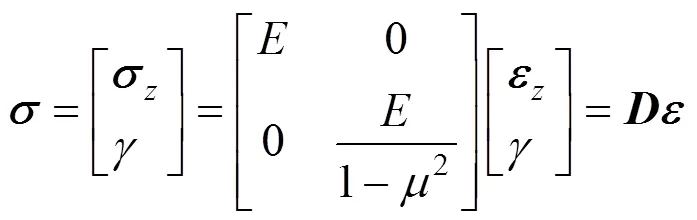
式中:为材料弹性模量;为泊松比。
3.3 单元平衡方程组
单元弹性应变能的一般表达式为
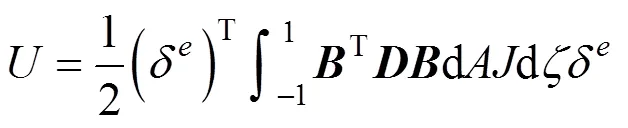
假设箱梁单元上作用均布荷载q,q和q,则外部荷载作用下的外荷载势能为
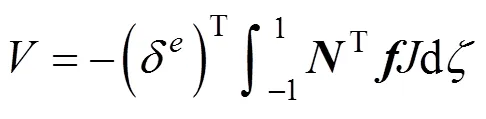
其中:为单元的外荷载矩阵,其具体形式参考文献[14]进一步得出。
基于最小势能原理得到三节点变截面箱梁段等参有限元的平衡方程组:
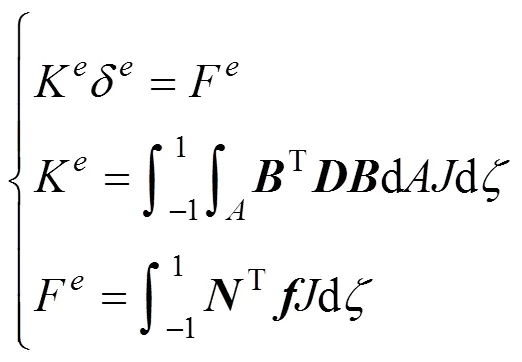
采用高斯积分计算得出变截面梁单元的单元刚度矩阵和节点等效荷载列阵,并基于MATLAB编写了相关理论的有限元计算程序。程序编写的一般流程如下。
1) 结构参数输入:节点坐标、截面几何尺寸、材料特性、荷载类型和约束条件等;
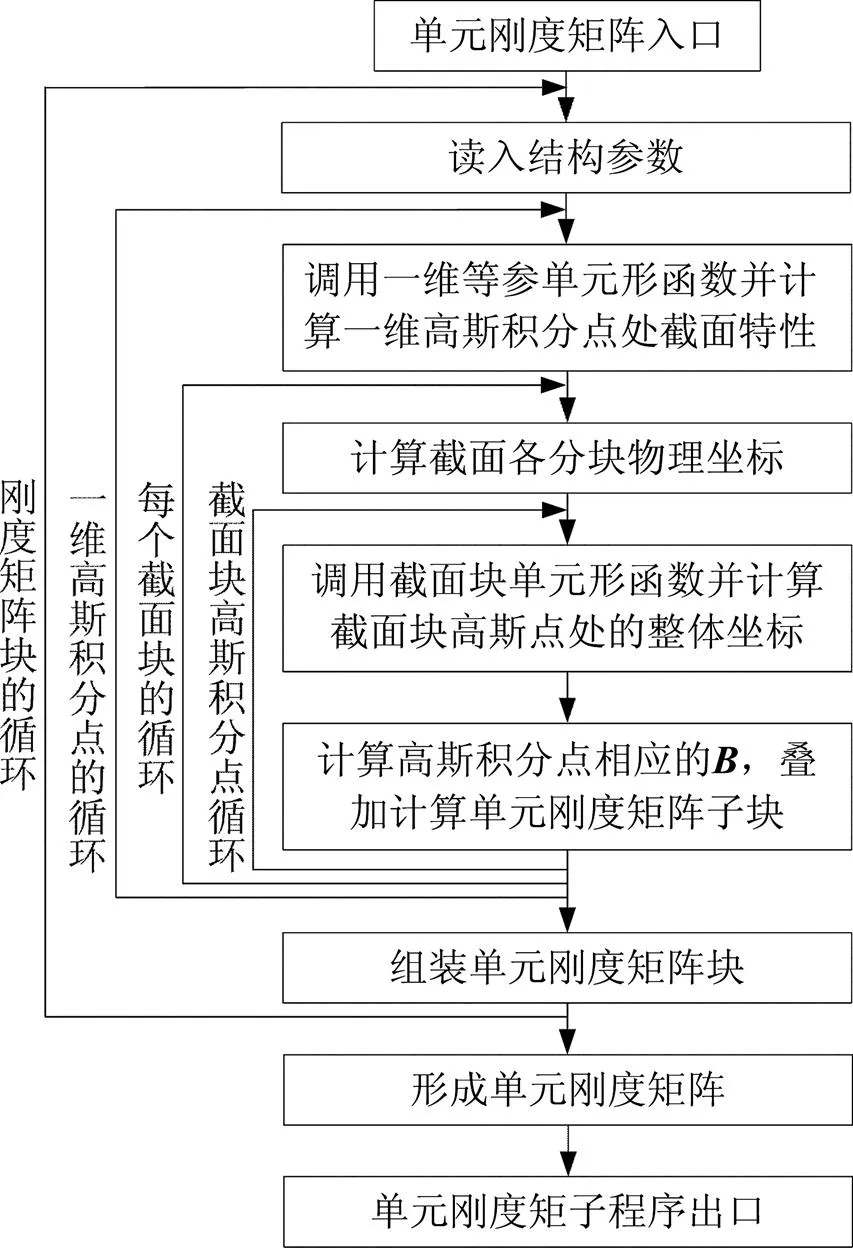
图4 单元刚度矩阵子程序的流程图
2) 计算单元刚度矩阵并组合形成整体刚度 矩阵;
3) 计算单元等效荷载列阵并组合形成整体荷载列阵;
4) 给定边界条件;
5) 分析求解。
单元刚度矩阵是有限元分析的重要部分,单元刚度矩阵计算子程序的编程框图如下:
4 实验模型验证
如图5(a)所示,一座有机玻璃制成的三跨变截面连续梁桥模型,其计算跨径为460 mm+860 mm+ 460 mm,变截面部分的高度按照=0.0252+40的二次抛物线变化。横截面的设计尺寸如图5(b)所示,除了箱梁高度变化外,其他的几何参数均保持不变。所用有机玻璃的弹性模量为=2 600 MPa,泊松比=0.4。罗旗帜[8]已测出作用集中力(= 173.33 N)和整桥作用均布荷载(=500 N/m)2种工况下截面I上各测点的正应力大小。
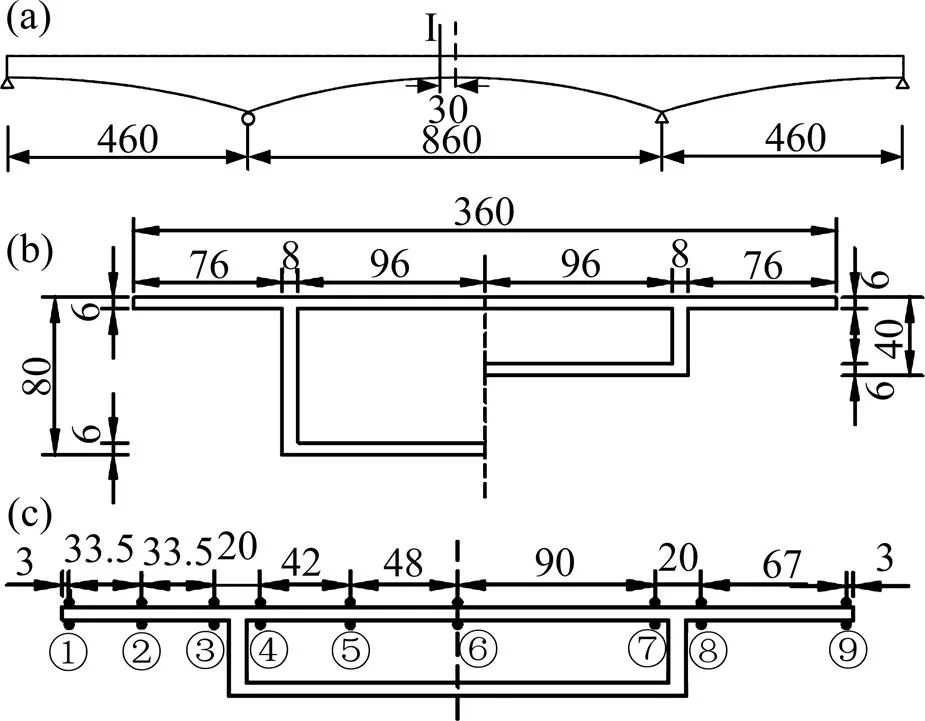
单位:mm
采用本文提出的三节点梁段法,将上述模型划分为19个梁段单元,共39个节点。利用编写的计算程序分别求出集中荷载和均布荷载作用下I-I截面上各测点的应力值,并与实测结果、有限段法和ANSYS数值结果进行对比分析。
由表1和2可知,无论在集中荷载或均布荷载作用下,截面上各测点的梁段法计算值与实测结果、有限段法和ANSYS数值结果均吻合较好;梁段法计算值相对于实测结果的最小绝对误差分别为1.62%和0.36%,最大绝对误差分别为10.19%和14.36%。综上所述,该算例验证了理论公式推导及其编写程序的正确性和有效性,能满足工程精度要求并适用于变截面箱梁的剪力滞效应的计算与 分析。
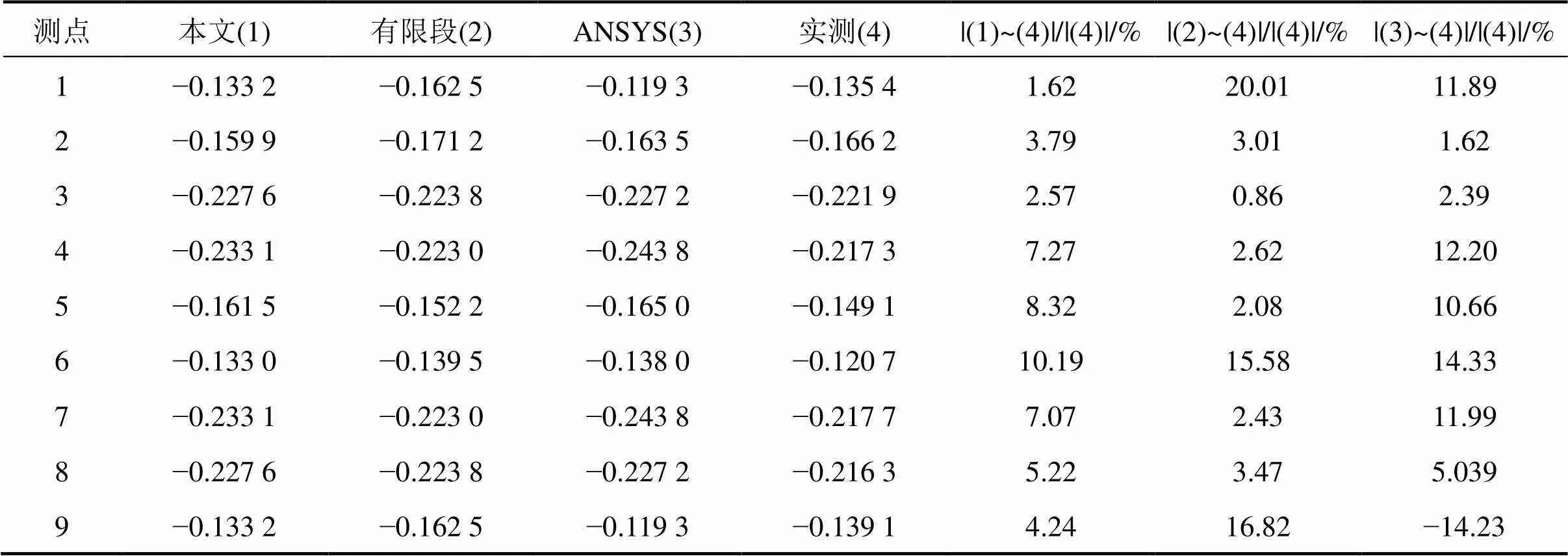
表1 集中荷载作用下截面I处应力分布
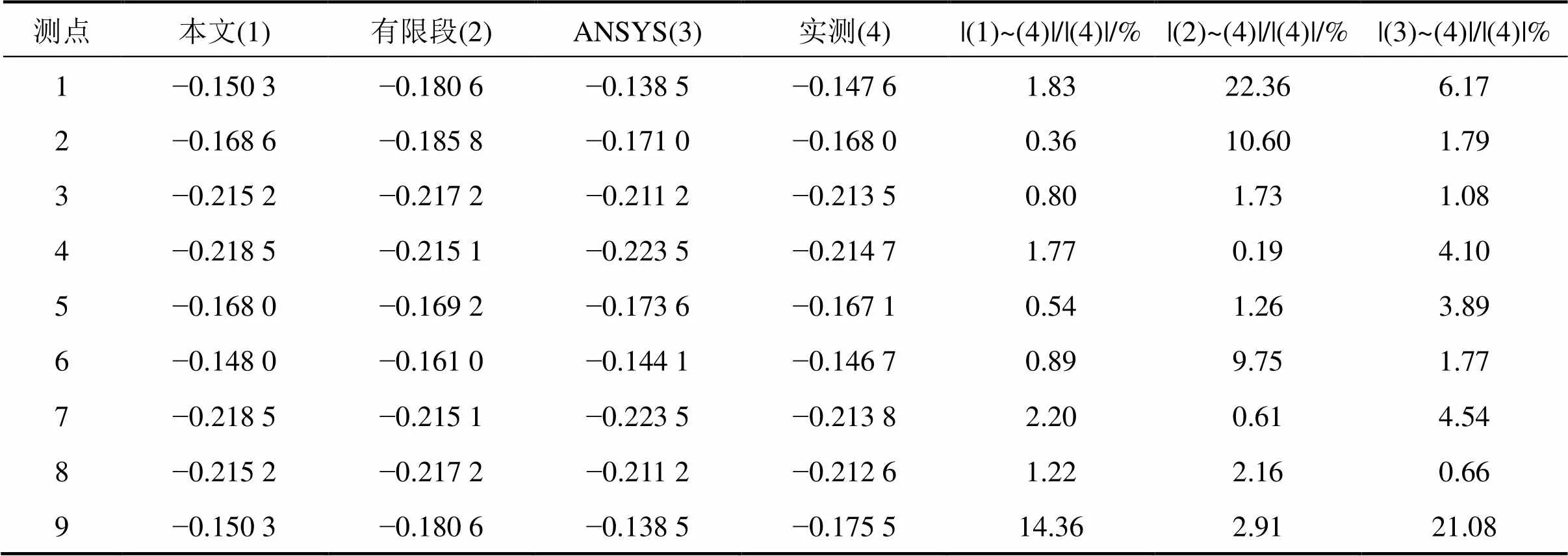
表2 均布荷载作用下截面I处应力分布
5 参数敏感性分析
计算钢−混组合箱梁剪力滞效应时,混凝土板与钢板之间的滑移对剪力滞效应影响较小,往往可以忽略剪力连接度的影响[16]。现选取某市轨道交通线上一座三跨变截面钢-混组合连续梁桥,分析梁高变化形式、混凝土强度、腹板斜率、翼宽比和宽跨比等因素对组合箱梁典型截面I-I和II-II处剪力滞效应的敏感性。
如图6(a)所示,连续梁桥的跨径组合为48 m+80 m+48 m,箱梁高度按照2次抛物线变化外,其他的几何参数均保持不变,截面尺寸见图6(b);该桥主梁顶板为C50混凝土,腹板和底板为Q345钢;考虑2种工况:1)集中荷载=10 kN作用于中跨跨中;2) 整桥作用均布荷载=1 kN/m。
5.1 梁高变化形式的敏感性分析
工程中变截面箱梁高度的变化常通过指数函数的幂次方变化来实现,常采用次方数为1.3,1.5, 1.8,2.0和2.2次。
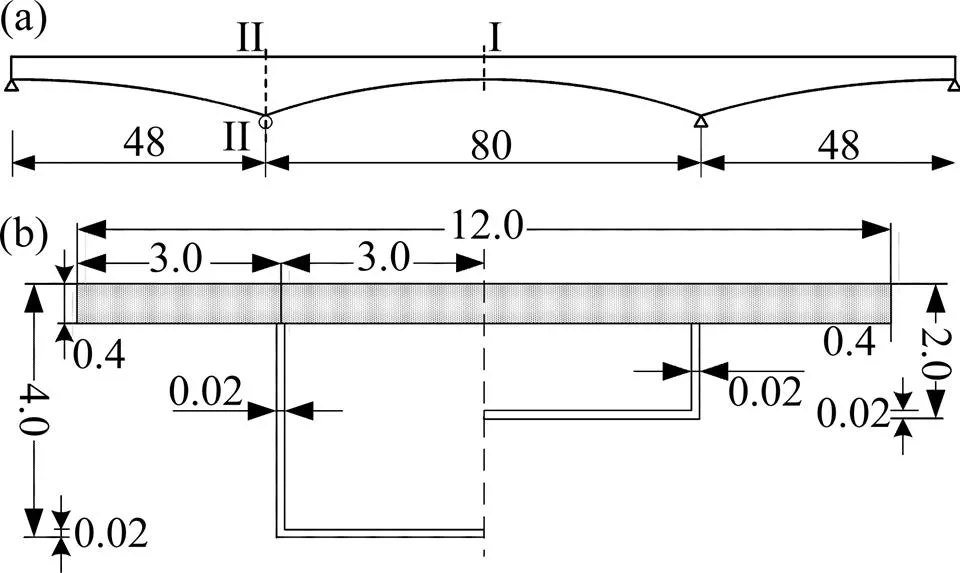
单位:m
图7给出了梁高变化形式对截面I-I和II-II顶板剪力滞效应敏感性的影响。随着次方数的逐渐增大,集中荷载作用下,截面I-I腹板处剪力滞系数从1.035增大到1.039,翼缘板自由端处剪力滞系数从0.994减小到0.988;均布荷载下,截面I-I腹板处剪力滞系数从1.024增大到1.026,翼缘板自由端处剪力滞系数从0.989减小到0.983。2种荷载下,截面II-II剪力滞系数的变化规律和截面I-I相同,腹板处剪力滞效应与幂次方数呈正相关的关系,翼缘板处剪力滞效应与幂次方数呈负相关的关系。敏感性分析结果表明,2种加载方式下,梁高变化形式对剪力滞效应的影响不明显。
5.2 混凝土强度的敏感性分析
选取C40~C80的混凝土强度,分析集中荷载和均布荷载作用下混凝土强度对剪力滞效应的敏 感性。
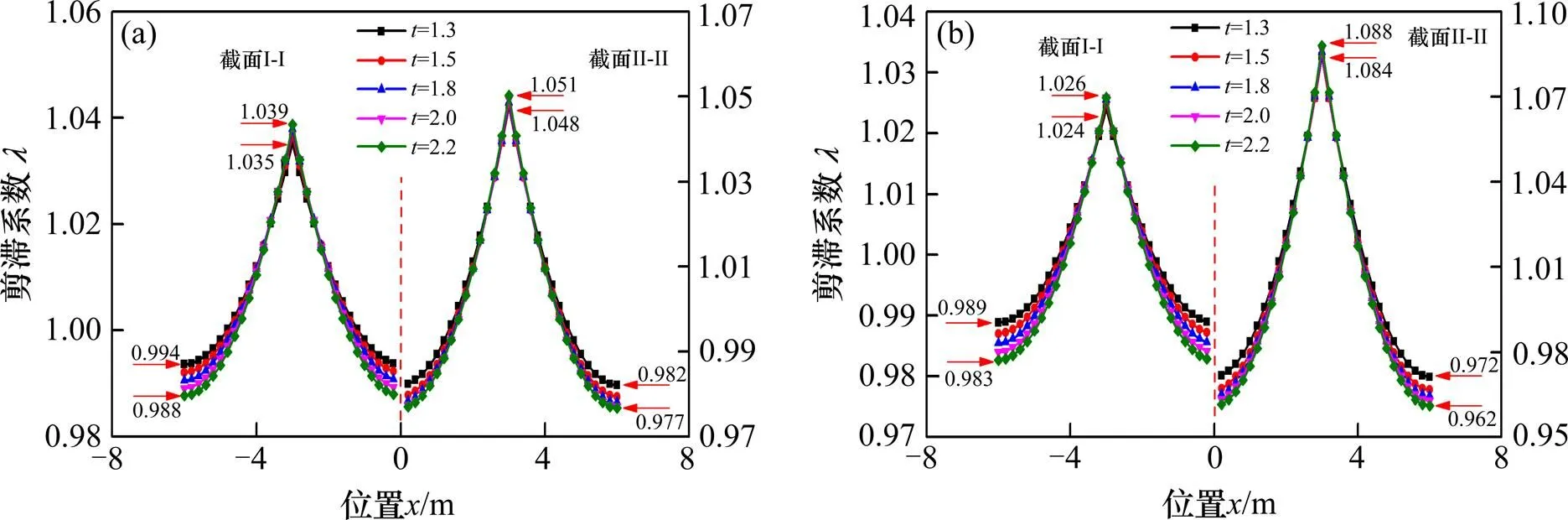
(a) 集中荷载;(b) 均布荷载
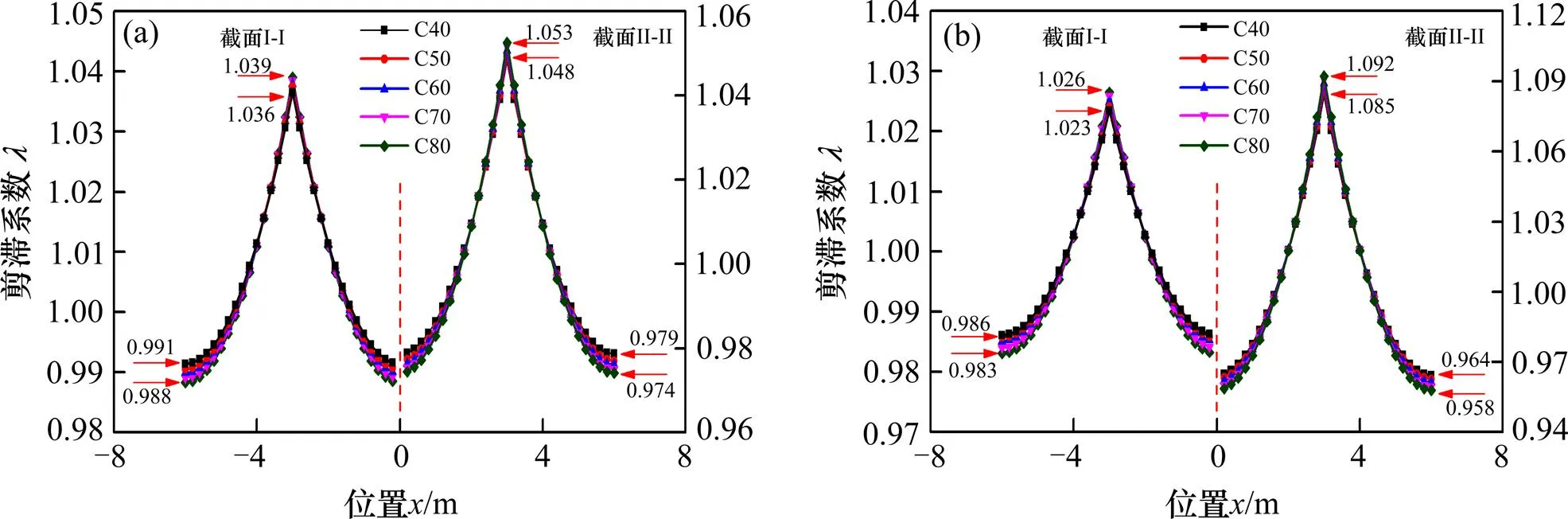
如图8所示,随着混凝土强度逐渐增大,集中荷载作用下,截面I-I腹板处剪力滞系数从1.036增加到1.039,翼缘板自由端处剪力滞系数从0.991减小到0.988;均布荷载作用下,腹板处剪力滞系数由1.023增大到1.026,而翼缘板自由端处剪力滞系数则由0.986减小到0.983。2种荷载下,截面II-II具有和截面I-I相同的剪力滞系数变化规律。敏感性分析结果表明,2种加载方式下,混凝土强度变化对剪力滞效应的影响不明显。
5.3 腹板斜率的敏感性分析
为研究不同腹板倾斜度下箱梁的剪力滞效应,倾斜角分别取70°,75°,80°,85°和90°,为便于剪力滞系数比较,通过改变混凝土底板宽度来实现α的不同。
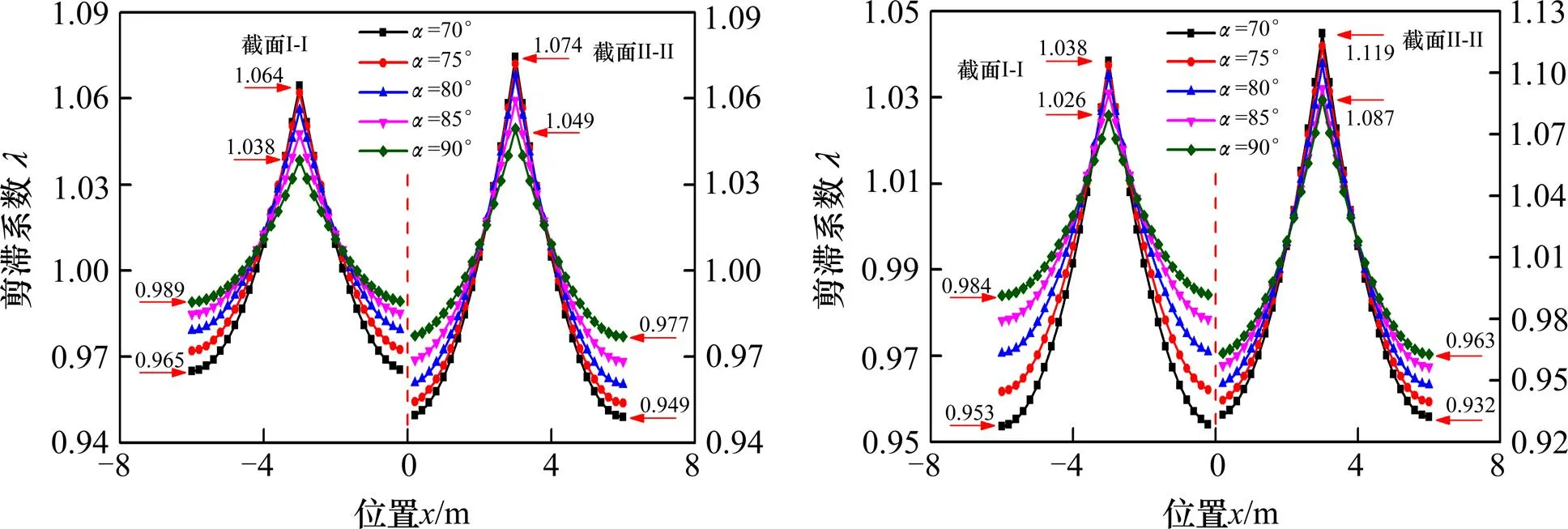
图9是倾斜角的敏感性分析,随着倾斜角从70°增加到90°,集中荷载作用下,截面I-I腹板处剪力滞系数从1.064减小到1.038,翼缘板自由端处剪力滞系数从0.965增加到0.989;均布荷载作用下,截面I-I腹板处剪力滞系数从1.038减小到1.026,翼缘板自由端处剪力滞系数从0.953增加到0.984。2种荷载下,截面II-II具有和截面I-I相同的剪力滞系数变化规律。敏分析结果表明,腹板倾斜度是变截面连续箱梁剪力滞效应分析时值得考虑的影响因素,倾斜角为90°时,剪力滞效应最小。
(a) 集中荷载;(b) 均布荷载
(a) 集中荷载;(b) 均布荷载
5.4 翼宽比的敏感性分析
翼宽比被定义为混凝土悬臂板b与顶板宽度b之比,通过改变悬臂板宽度,取翼宽比分别为0.2, 0.4,0.6,0.8和1.0。
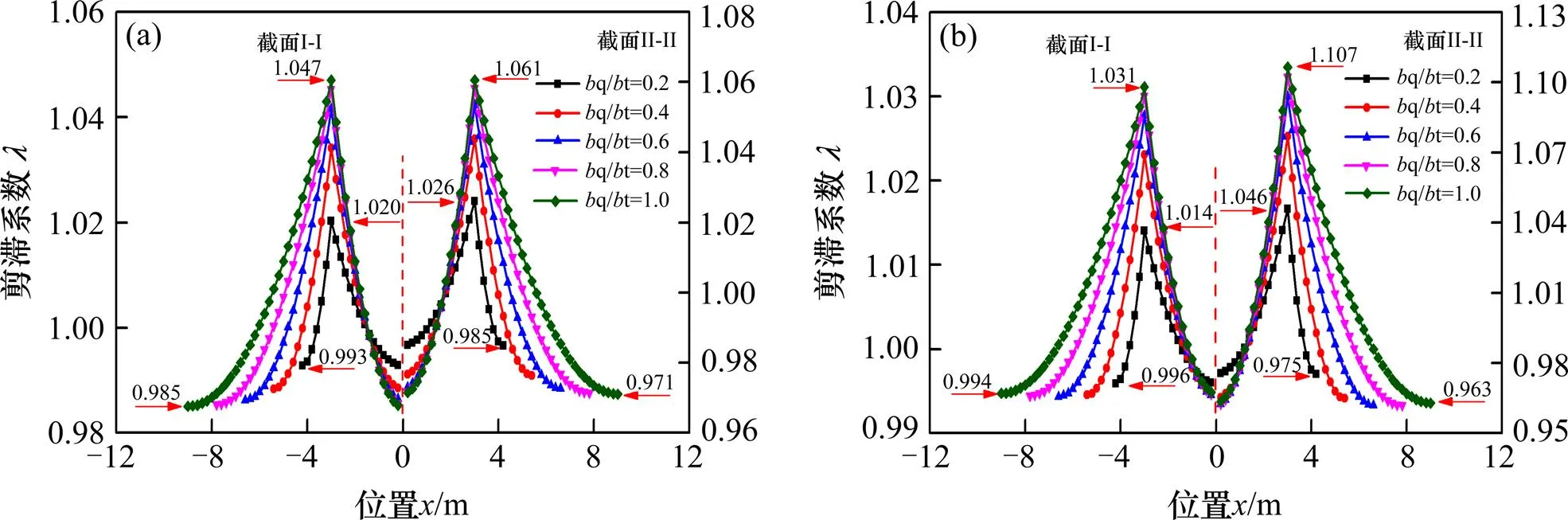
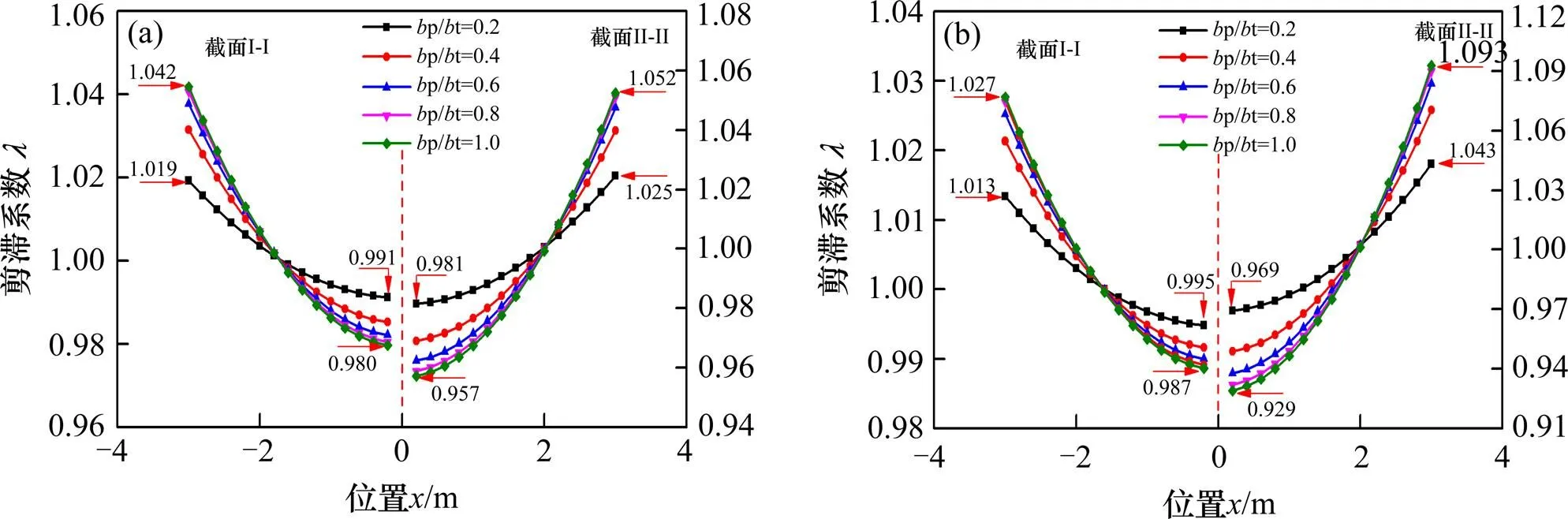
图10和图11分别是不同翼宽比的敏感性分析结果。当翼宽比从0.2增加到1.0时,集中荷载作用下,截面I-I顶板的腹板处剪力滞系数从1.020增加至1.047,翼缘板自由端处剪力滞系数从0.993减小至0.985;截面I-I底板的腹板处剪力滞系数从1.019增加至1.042,底板中点处剪力滞系数从0.991减小至0.980。均布荷载作用下,截面I-I顶板腹板处剪力滞系数从1.014增加至1.031,翼缘板自由端处剪力滞系数从0.996减小至0.994;截面I-I底板腹板处剪力滞系数从1.013增加至1.027,底板中点处剪力滞系数从0.995减小至0.987。2种荷载下,截面II-II顶板和底板上剪力滞系数的变化规律与截面I-I相同,前者剪力滞效应较后者明显。分析结果表明,翼宽比小于0.6时,剪力滞效应随翼宽比的增大而增大,但翼宽比大于0.6时,翼宽比变化对剪力滞系数变化的影响较小。
5.5 宽跨比的敏感性分析
宽跨比定义为顶板宽度b与中跨跨长之比,保持箱梁顶部宽度不变及边跨长恒等于0.6倍的中跨长,中跨长度分别取60,80,100,120和150 m,相应的宽跨比分别为0.100,0.075,0.060,0.050和0.040。
(a) 集中荷载;(b) 均布荷载
(a) 集中荷载;(b) 均布荷载
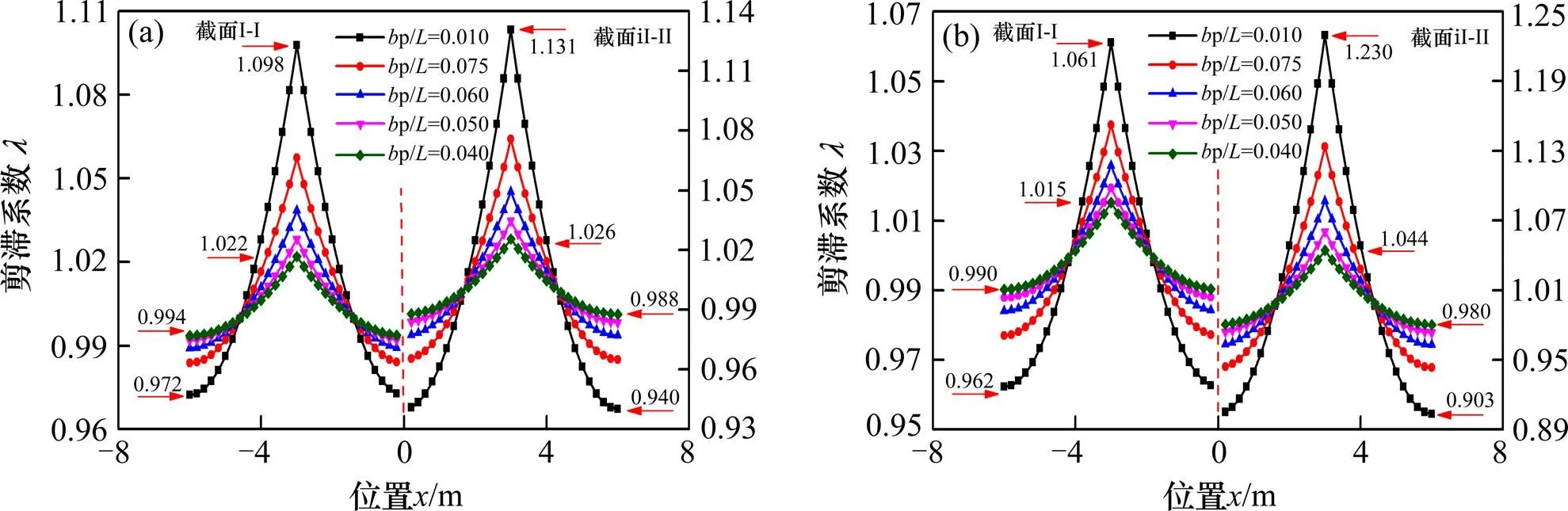
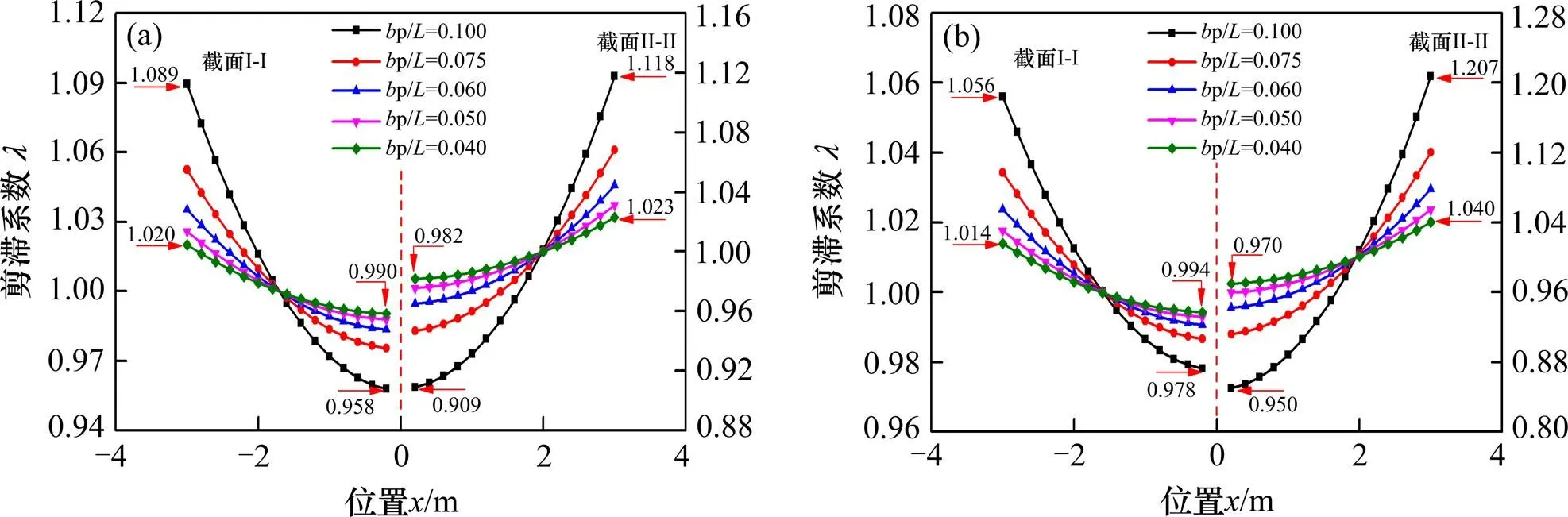
如图12和图13所示,随中跨长度从60 m增加到150 m,集中荷载作用下,截面I-I顶板的腹板处剪力滞系数明显减小,其值从1.098减小到1.022,悬臂板自由处剪力滞系数从0.972增加到0.994;截面I-I底板的腹板处剪力滞系数从1.089减小到1.020,底板中点处剪力滞系数从0.958增加到0.990。均布荷载作用下,截面I-I顶板的腹板处剪力滞系数从1.061减小到1.015,翼缘板自由端处剪力滞系数从0.962增加到0.990;截面I-I底板的腹板处剪力滞系数从1.056减小到1.014,底板中点处剪力滞系数从0.978增加到0.994。2种荷载作用下,截面II-II顶板和底板上剪力滞系数的变化规律与截面I-I相同,前者剪力滞效应较后者明显。分析结果表明,宽跨比是箱梁模型中剪力滞效应分析的主要影响因素,宽跨比越大,剪力滞效应越明显。
将上述三跨变截面连续箱梁剪力滞效应的参数敏感性分析结果与文献[17]中等截面钢−混简支箱梁剪力滞效应的参数敏感性分析结果进行对比。对比结果表明,影响箱梁剪力滞效应的主要因素为宽跨比和翼宽比,且荷载类型对箱梁剪力滞效应有一定的影响;同时,变截面连续箱梁中腹板倾角的变化对剪力滞效应变化程度的影响较等截面简支箱梁明显。
(a) 集中荷载;(b) 均布荷载
(a) 集中荷载;(b) 均布荷载
6 结论
1) 基于选定的二次抛物线剪力滞翘曲位移函数,提出了分析变截面连续箱梁剪力滞效应的三节点板元梁段法,并利用最小势能原理推导出相应的等参有限元行列式。算例模型的数值结果与实测值吻合良好,且利用较少单元就可以获得满意的剪力滞效应分析结果。
2) 集中荷载和均布荷载2种工况下,变截面连续箱梁剪力滞效应的敏感性分析结果表明:影响变截面箱梁剪力滞效应的主要因素依次为宽跨比、翼宽比及腹板倾角,而荷载类型对箱梁剪力滞效应也有一定的影响。
3) 随着宽跨比的增大,剪力滞效应逐渐增大且变化趋势逐渐明显;随着翼宽比的增加,剪力滞效应虽然逐渐增大但变化趋势逐渐减弱;相反,随着腹板倾角的增大,剪力滞效应逐渐减小,且腹板倾角变化对变截面箱梁剪力滞效应变化程度的影响较等截面箱梁明显。
[1] 邵旭东, 顾安邦. 桥梁工程[M]. 4版. 北京: 人民交通出版社, 2016:87−90. SHAO Xudong, GU Anbang. Bridge engineering[M]. 4th ed. Beijing: China Communication Press, 2016: 87−90.
[2] 孙璐, 王文雷, 吴国琦, 等. 客运专线箱梁端部裂纹成因分析及施工控制[J]. 铁道工程学报, 2007, 24(10): 44−49. SUN Lu, WANG Wenlei, WU Guoqi, et al. Analyses of the causes for crack on the end side of box girder for railway passenger dedicated line and its construction control[J]. Journal of Railway Engineering Society, 2007, 24(10): 44−49.
[3] 张元海, 胡玉茹, 林丽霞. 基于修正翘曲位移模式的薄壁箱梁剪力滞效应分析[J]. 土木工程学报, 2015, 48(6): 44−50. ZHANG Yuanhai, HU Yuru, LIN Lixia. Analysis on shear lag effect of thin-walled box girders based on a modified warping displacement mode[J]. Journal of Civil Engineering, 2015, 48(6): 44−50.
[4] CHANG S T, YUN D. Shear lag effect in box girder with varying depth[J]. Journal of Structural Engineering, 1988, 114(10): 2280−2292.
[5] 周勇超, 郝宪武, 李子青. 变截面波形钢腹板组合梁剪力滞效应[J]. 长安大学学报(自然科学版), 2014, 34(4): 62−69. ZHOU Yongchao, HAO Xianwu, LI Ziqing. Shear lag effect of non-uniform composite beam with corrugated steel web[J]. Journal of Changan University (Nature Science), 2014, 34(4): 62−69.
[6] 刘世忠, 欧阳永金, 吴亚平. 变截面薄壁箱梁剪力滞剪切变形效应分析[J] .中国公路学报, 2002, 15(3): 61−67. LIU Shizhong, OUYANG Yongjin, WU Yaping, et al. Non-uniform thin wall box analysis of considering both shear lag and shear deformation[J]. China Journal of Highway & Transport, 2002, 15(3): 61−67.
[7] 罗旗帜. 变截面多跨箱梁桥剪滞效应分析[J]. 中国公路学报, 1998, 11(1): 63−70. LUO Qizhi. Analysis of the shear lag effect on continuous box girder bridges with variable depth[J]. China Journal of Highway and Transport, 1998, 11(1): 63−70.
[8] 吴幼明, 罗旗帜, 岳珠峰. 薄壁箱梁剪力滞计算的梁段有限元法[J]. 中国铁道科学, 2003, 24(4): 64−68. WU Youming, LUO Qizhi, YUE Zhufeng. Finite element method for calculating the shear lag in box girders[J]. China Railway Science, 2003, 24(4): 64−68.
[9] ZHANG Y H, LIN L X. Shear lag analysis of thin-walled box girders based on a new generalized displacement[J]. Engineering Structures, 2014, 61(1): 73−83.
[10] 何志刚, 蔺鹏臻. 考虑截面配筋的变截面悬臂梁剪力滞效应研究[J]. 铁道科学与工程学报, 2017, 14(10): 2154−2161. HE Zhigang, LIN Pengzhen. Study on shear lag effect of varying section cantilever beam in consideration of section reinforcement[J]. Journal of Railway Science and Engineering, 2017, 14(10): 2154−2161.
[11] 韦成龙, 李斌, 曾庆元. 变截面连续箱梁桥剪力滞及剪切变形双重效应分析的传递矩阵法[J]. 工程力学, 2008, 25(9): 111−117. WEI Chenglong, LI Bin, ZENG Qingyuan. Transfer matrix method considering both shear lag and shear deformation effects in non-uniform continuous box girder[J]. Engineering Mechanics, 2008, 25(9): 111−117.
[12] 丁南宏, 林丽霞, 钱永久. 变截面箱梁剪力滞及剪切变形效应近似计算方法[J]. 铁道科学与工程学报, 2011, 8(1): 14−18. DING Nanhong, LIN Lixia, QIAN Yongjiu. An approximate method to analyze the effect of shear lag and shear deformation of box beam with varing depth[J]. Journal of Railway Science and Engineering, 2011, 8(1): 14−18.
[13] 魏丽娜, 方放, 余天庆, 等. 变截面箱形梁桥剪滞效应的近似计算方法[J]. 土木工程学报, 1997, 2(1): 64−72. WEI Lina, FANG Fang, YU Tianqing, et al. An approximate method for calculating shear lag in variable cross-section box girders[J]. China Civil Engineering Journal, 1997, 2(1): 64−72.
[14] 王银辉, 陈山林. 考虑初曲率影响的变曲率箱梁空间有限元分析[J]. 中国公路学报, 2007, 20(6): 18−21.WANG Yinhui, CHEN Shanlin. Spatial finite element analysis for variable-curvature box girder with initial curvature[J]. China Journal of Highway and Transport, 2007, 20(6): 18−21.
[15] Høgsberg J, Krenk S. Analysis of moderately thin-walled beam cross-sections by cubic isoparametric elements[J]. Computers & Structures, 2014, 134(4): 88−101.
[16] 孙林林, 蒋丽忠, 周旺保. 钢−混凝土组合箱梁剪力滞系数实用计算方法[J]. 铁道科学与工程学报, 2017, 14(6): 1289−1295. SUN Linlin, JIANG lizhong, ZHOU Wangbao. Practical calculation method of shear lag coefficient of steel-concrete composite box beam[J]. Journal of Railway Science and Engineering, 2017, 14(6): 1289−1295.
[17] HU S, YU J, WEI C, et al. Shear lag behavior and parametric sensitivity analysis of steel–concrete composite structure with double-box[J]. Archive of Applied Mechanics, 2017, 87(10): 1−15.
Board beam segment method for calculating shear lag of thin-walled box girder with variable section
LI Linan1, 2, GENG Wenbin1, LIU Xijun1, 2, ZHANG Qing1, ZHOU Cong1
(1. Mechanical Engineering of Tianjin University, Tianjin 300350, China; 2. Tianjin Key Laboratory of Modern Engineering Mechanics, Tianjin 300350, China)
In order to calculate shear lag effect of Thin-walled box girder with variable section and analyse parametric sensitivity, this paper presents a three nodes board beam segment method considering shear lag effect. Based on the relation among strain, displacement and deformation in box girder section, and regarding shape functions as interpolation functions of variable height within element, the determinant of isoparametric finite element corresponding to beam segment method had been established by using the minimum potential energy principle. Computing a model by using the complied finite element program, whose theoretical results agree well with experimental value and the finite element results, it verified the correctness and reliability of the theoretical method and deduced formulas; Finally, the parametric sensitivity analysis about some common influence factors was also launched under concentrated and uniform load, when analyzing shear lag of thin-walled box girder with variable cross section. The results show that the flange width ratio, width span ratio and inclination of webs are the main factors that influence the shear lag of box girder with variable section. The accuracy and efficiency of the method given in the paper can provide certain reference value for the shear lag effect of box girder with variable section.
variable section; thin-walled box girder; shear lag effect; parametric sensitivity; isoparametric finite element
10.19713/j.cnki.43−1423/u.2019.02.017
U448.21
A
1672 − 7029(2019)02 − 0408 − 11
2018−03−08
国家自然科学基金资助项目(11572218)
李林安(1966−),男,山西吕梁人,教授,博士,从事桥梁与结构工程研究;E−mail:lali@tju.edu.cn
(编辑 蒋学东)
