不同因素对填筑路堤边坡稳定性影响分析

2021-05-19王鹏

黑龙江交通科技 2021年4期

关键词：坡坡摩擦角安全系数

王鹏

(中铁十四局集团有限公司，山东济南 250000)

1 工程实例

1.1 工程简介

松山湖站位于东莞市松山湖景区新城路与沁园路交叉口，为地下二层双岛式站台，呈南北向布置，与规划3#线同台换乘，并设置联络线，总长度为404.1 m，标准段宽度为49.9 m，采用明挖法施工。

新城路西侧机动车道及人行道在施工场地内，需要临时占用，根据占一还一的原则，需在新城路西侧修建由北向南的交通疏解道，道路等级为城市主干路，设计车速60 km/h，由左向右为0.5 m坡肩+3 m人行道+14 m机动车道，采用水泥混凝土路面。

1.2 工程地质

松山湖站属于剥蚀残丘地貌，地表层局部可见第四纪沉积层，地形地貌比较开阔平缓，坡度一般在10°以下，水系不发育。拟建工程区域内人工填土广泛分布，主要为回填的黏性土、砂土、碎石等。

1.3 路基边坡

交疏疏解道填筑高度最高约为5 m，采取分层回填、分层碾压，现场试验测得压实度均在96 %以上，符合设计和规范要求，边坡设计坡率为1∶1.5，边坡填筑完成后沿路线走向每隔10 m测量一下边坡坡率，现场实测边坡坡率为1∶1.5～1∶2.02。

2 数值模拟分析

2.1 强度折减法基本原理

FLAC3D是率先将连续体快速拉格朗日分析法应用于岩土工程问题上，在解决相关问题上具有许多优越性，可对岩石、边坡等建立模型并进行数值分析。

强度折减法是将强度折减技术与数值模拟方法相结合，通过调整折减系数对边坡的稳定性进行分析。基本原理是将坡体原始粘聚力c和内摩擦角φ同时除以折减系数K，得到一组新的粘聚力c′和内摩擦角φ′，作为新的参数反复进行数值模拟，直至边坡达到临界破坏状态，原始强度指标与临界破坏状态的强度指标之比即为该边坡的安全系数Fs。

2.2 数值模型

路基填筑高度为5 m、坡率为1∶1.5时数值模型如图2，绿色部分为路基，蓝色部分为地基，路基顶面宽度为17.5 m、底面宽度为25 m，地基高度为10 m，地基宽度为35 m，沿纵向长度为2 m。固定约束地基底面、四周，路基顶面不约束，模型共划分7 600个网格单元，10 005个节点。

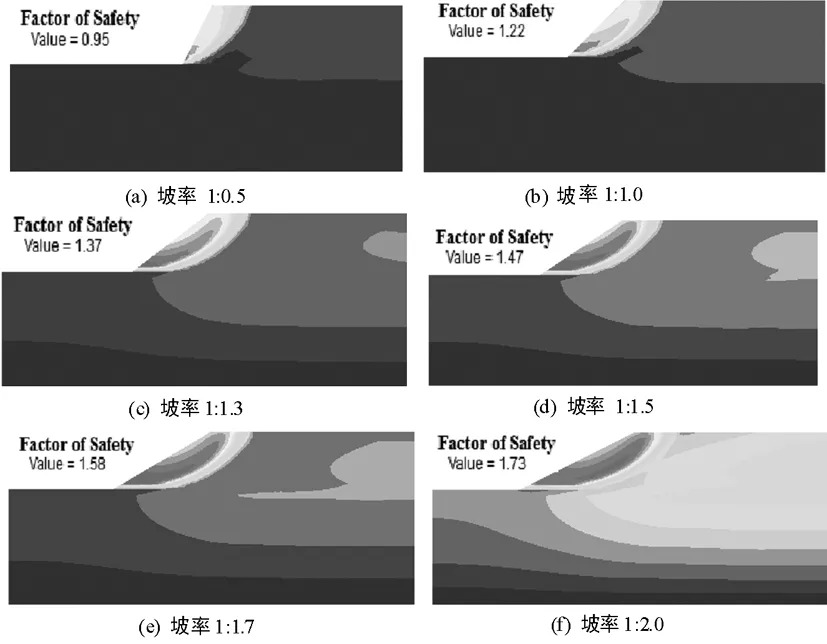
图2 不同坡率模拟云图

2.3 物理力学参数

根据地质勘探钻孔取样试验得出地基物理力学参数，填筑土体及地基物理力学参数如表1。

表1 物理力学参数

2.4 数值模拟结果分析

建立模型后进行数值模拟，结果如图1所示。边坡安全系数为1.47，《铁路路基设计规范》规定路基边坡稳定安全系数不得小于1.25，因此该边坡安全系数满足规范要求。

图1 数值模拟云图

路基边坡坡角向上0.5～1 m范围内位移最大为14.699 cm，沿滑坡体向上位移逐渐减小，坡顶位移为8.4 cm，路基中部位移变化不大，从路基中部至坡面位移逐渐增大，塑性区滑坡体未贯通，边坡稳定性和安全性较好。

3 影响因素分析

3.1 边坡坡率对安全系数影响

分别建立边坡坡率为1∶0.5、1∶0.7、1∶1.0、1∶1.3、1∶1.5、1∶1.7、1∶2.0、1∶3.0的边坡模型并分别进行数值模拟，模型的物理力学参数均保持一致。部分坡率数值模拟结果如图2所示。分析模拟数据得出边坡安全系数与坡率的关系曲线如图3所示。

图3 安全系数与坡率关系

由图2、图3分析可知，随着坡率的增大，边坡安全系数逐渐增大，安全系数随坡率的增加近似呈线性关系增长，坡率为1∶0.5、1∶0.7、1∶1.0的安全系数分别为0.95、1.07、1.22，均小于1.25，不满足规范要求，边坡稳定性较差，容易发生滑坡等事故。坡率越大安全系数越高，边坡稳定性、安全性越好。

通过origin拟合得出安全系数与坡率的关系式

Fs=0.517 4L+0.697

(1)

式中:Fs为安全系数；L为边坡坡率；回归系数R2=99.98%。

3.2 边坡坡角对安全系数影响

由坡率数值模拟得出安全系数与边坡坡角的关系，边坡坡角分别为18.4°、26.6°、30.5°、33.7°、37.6°、45°、55°、63.5°的安全系数分别为2.25、1.73、1.58、1.47、1.37、1.22、1.07、0.95，安全系数与坡角的关系曲线如图4所示。

图4 安全系数与坡角关系

由图4分析可知，边坡安全系数随着坡角的增大而逐渐减小，坡角大于45°时，边坡安全系数小于1.25，不满足规范要求，边坡稳定性较差。通过origin拟合出边坡安全系数与坡角的幂函数关系式

Fs=16.897θ-0.693

(2)

式中:Fs为安全系数；θ为坡角，°；回归系数R2=99.96%。

3.3 填筑高度对安全系数影响

填筑高度对边坡稳定产生一定的影响，填筑高度越高，在填筑体自重及外荷载作用下，可能出现滑坡现象。为研究填筑高度对边坡稳定性的影响，基于上文建模的基础上分别建立填筑高度为2 m、3 m、4 m、5 m、6 m、7 m的边坡模型并进行数值模拟，物理力学参数均保持一致，分析数据拟合得出边坡安全系数与填筑高度的关系曲线如图5所示。

图5 安全系数与填筑高度关系

通过origin软件拟合出边坡安全系数与路基填筑高度的关系可用幂函数表达

Fs=6.816 8H-0.94

(3)

式中：Fs为安全系数；H为路基填筑高度，m；回归系数R2=99.17%。

3.4 粘聚力和内摩擦角对安全系数影响

采用单因素法分别改变粘聚力和内摩擦角的参数研究分析粘聚力和内摩擦角对安全系数的影响，粘聚力分别为12 KPa、16 KPa、20 KPa、24 KPa、28 KPa、32 KPa，内摩擦角分别为10°、14°、18°、22°、26°、30°，每次模拟只改变一个参数，其余参数保持不变，共进行36次数值模拟，通过origin拟合得出安全系数与粘聚力、内摩擦角关系如图6所示。