带标准Brown运动扰动风险模型的破产概率模拟计算

王 琪， 薛 红， 陈毛毛

(西安工程大学理学院， 西安 710600)

引 言

破产概率是衡量金融风险和保险公司经营稳健性的重要尺度。关于破产理论的研究起源于由Lundberg和Cramér提出的L-C经典风险模型[1]。文献[2]讨论了经典风险模型最终破产概率的解析表达式，因有限时破产概率并没有具体的计算公式，文献[3]利用Monte-Carlo方法对经典风险模型在有限时间内的破产概率值进行了模拟计算。当索赔到达过程不依赖于独立性假设时，文献[4]分析了风险模型有限时破产概率的渐近性。此外，许多学者对L-C经典风险模型做了如下推广：一方面，在对保险公司的历史理赔额数据进行分析后发现，相较于轻尾分布而言，重尾分布更适合刻画实际中的理赔额分布。当不考虑风险干扰时，唐启鹤[5]等得到了重尾索赔风险模型最终破产概率的一个等价式，文献[6]讨论了当重大索赔额服从广义Pareto分布时的最终破产概率估计值。文献[7]基于条件泊松过程的空间分析法，讨论了路径依赖重尾索赔风险模型的渐近有限时间破产概率。另一方面，由于现实中存在着投资收益和通货膨胀等干扰因素，故加入扰动项的风险模型会更贴合实际，Gerber在文献[8]中首次用标准Brown运动来刻画风险干扰，并将其引入经典风险模型。当索赔额序列服从指数分布，理赔次数服从Poisson过程时，文献[9]讨论了带标准Brown运动扰动风险模型的最终破产概率表达式，文献[10]用鞍点法分析了最终破产概率的上下界。

当索赔额序列服从重尾分布时，带标准Brown运动扰动风险模型的破产概率没有解析表达式，故本文提出了一种有效的带标准Brown运动扰动风险模型盈余轨道的模拟程序，运用MATLAB R2016a软件对带标准Brown运动扰动风险模型在有限时间内的破产概率进行Monte-Carlo模拟计算。并综合考虑小额索赔、办公用品、佣金等其他营业支出以及风险干扰等影响因素，结合保险公司实际数据，对该公司在有限时间内的破产概率进行了数值模拟计算，以期计算结果更加符合实际。

1 风险模型及破产概率模拟计算

1.1 经典风险模型

经典风险模型中，保险人在t时刻的盈余过程为[11]

(1)

其中：u是初始盈余，c为保费率即单位时间内的保费收入。{Xi,i≥1}是第i次理赔额，具有同分布A且均值为μA。{N(t),t≥0}服从参数为λ的Poisson过程，表示[0,t]内的理赔次数。

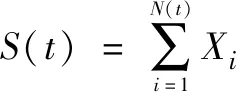
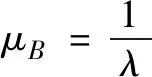
(2)

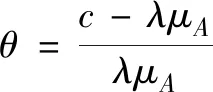
在风险模型中，若索赔额序列{Xi,i≥1}服从广义Pareto分布，索赔时间间隔序列{Wj,j≥1}服从均值为μB的指数分布，最终破产概率的渐近结果如定理2所述。

定理2[6]假设索赔额{Xi,i≥1}是一列非负的上广义负相依序列，具有共同分布A和有限均值μA；索赔时间间隔序列{Wj,j≥1}是一列广义负相依序列，具有共同分布和有限均值μB；并且索赔额序列{Xi,i≥1}与索赔时间间隔序列{Wj,j≥1}相互独立。若索赔额分布A属于重尾分布族中的控制变换尾分布族，同时安全负荷条件即κ=cμB-μA>0成立，则最终破产概率满足如下渐近结果：

(3)

1.2 经典风险模型的破产概率模拟计算

当索赔额服从重尾分布时，经典风险模型在有限时间内的破产概率没有明确表达式。结合经典风险模型盈余轨道的模拟程序思想[3]，假设索赔额序列服从广义Pareto分布，对有限时间内破产概率值进行Monte-Carlo模拟计算。步骤如下：

①以天为单位，选取研究的时间总长度T，将时间区间[0,T]平均等分为n份，s=T/n为每一时间区间的长度。记m为发生破产的次数。

②确定初始盈余值u，单位时间内的保费收入c。

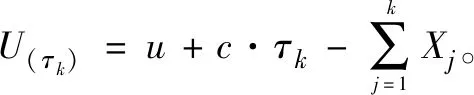
⑤重复第③步至第④步，利用MATLAB软件总共进行M次模拟。

⑥用m除以M可得到破产概率模拟值p。

例1对风险模型的参数及分布作如下假设：

(i) 以天为单位，初始盈余u=20，单位时间的保费收入c=5。

(ii) 索赔额序列{Xi,i≥1}服从参数为k1=0.0016,σ1=14.7580的广义Pareto分布F(x)=1-(1+kx/σ)-1/k，均值μA=15。

(iii)理赔次数{N(t),t≥0}服从参数为λ=1/5的 Poisson 过程，即索赔时间间隔序列{Wj,j≥1}服从均值为μB=5的指数分布。

取小时间区间的长度s=0.1天，总时间长度T=1年，模拟盈余轨道如图1所示。

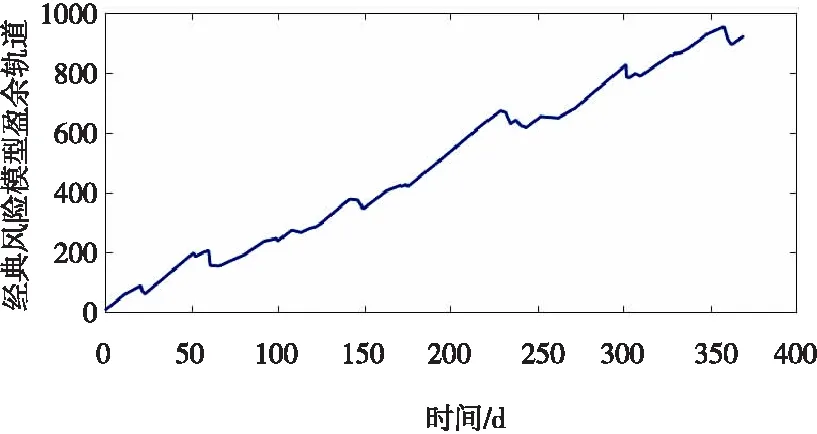
图1 经曲风险模型盈余轨道模拟图

取s=0.001年，改变T的取值，分别用MATLAB软件进行M=104次模拟，可得有限期内的破产概率模拟值，见表1。

表1 有限时间破产概率模拟值(重尾索赔)

根据例1中的假设，由式(3)计算得到最终破产概率值p1=0.3826。由表1可知，随年限增长，破产概率模拟数值逐渐接近于最终破产概率p1，表明数值模拟计算合理有效。

1.3 带标准Brown运动扰动风险模型

由于现实中存在着投资收益和通货膨胀等各种随机干扰因素，故加入扰动项的风险模型会更切合实际，Gerber[8]用标准Brown运动来刻画风险干扰，并将其引入经典风险模型，盈余过程为

(4)

其中：σ>0为波动常数，{B(t),t≥0}是标准Brown运动，其余符号意义同经典风险模型，该模型也称为跳-扩散风险模型。

若理赔次数服从参数为λ的Poisson过程，索赔额序列{Xi,i≥1}独立同分布于均值为μA的指数分布A(x)，彭勤文[9]利用鞅论中的收敛定理得到带扩散扰动风险模型的最终破产概率表达式。

定义1[12]设MX(r)为索赔额序列的矩母函数，则

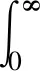
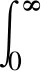
定理3[9]当σ≠0时，带标准Brown运动扰动风险模型的最终破产概率为

Ψ3(u)=(1+RμA)e-Ru

(5)

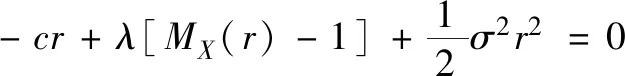
1.4 带标准Brown运动扰动风险模型的破产概率模拟计算

基于1.2节，本文设计了一种模拟带标准Brown运动扰动风险模型盈余轨道的程序思想，并结合Monte-Carlo方法，对风险模型在有限时间内的破产概率进行了模拟计算。步骤如下：

①选取研究的时间总长度T。将[0,T]等分为n等份，每一小区间长度为s. 则共有n+1个区间端点，记为{0,s,2s,…,ns}. 记m为发生破产的次数。

②确定初始盈余值U(0)=u，单位时间内保费收入c，波动常数σ的取值。

③由指数分布生成索赔时间间隔序列{Wj,j≥1}，并记录下索赔发生的时刻{τk,k≥1}。之后，生成服从A分布的索赔额序列{Xi,i=1,…,j}。再生成标准Brown运动随机数序列{Bhs,h=0,1,2,…,n}，它是独立的正态过程，且满足{B(h+1)s-Bhs}～N(0,s)。

④计算每一小时间区间[hs,(h+1)s]右端点时刻的盈余值，记为序列{Uh+1},(h=0,1,…,n-1)。若τk∈[hs,(h+1)s]，即在时间区间[hs,(h+1)s]上发生了额度为Xk的索赔，则不仅在右端点处加入扩散扰动项σ·B(h+1)s，同时也要减去索赔额Xk，计算公式为Uh+1=Uh+c·s+σ·B(h+1)s-Xk；若未发生索赔，则仅在右端点处加入扰动项即可，计算公式修改为Uh+1=Uh+c·s+σ·B(h+1)s。若Uh+1<0，则终止本次计算，破产次数m加1。否则继续计算下一区间右端点时刻的盈余值。

⑤重复第③步至第④步，利用MATLAB软件进行M次模拟。

⑥用m除以M可得到破产概率模拟值p。

例2对风险模型(4)的参数作如下假设：

(i) 以天为单位，初始盈余u=20，单位时间的保费收入c=5。

(ii) 索赔额序列{Xi,i≥1}独立同分布于均值为μA=15的指数分布。

(iii)理赔次数{N(t),t≥0}服从参数为λ=1/5的 Poisson 过程，即索赔时间间隔序列{Wj,j≥1}服从均值为μB=5的指数分布。

(iv) 取波动常数σ=15。

取小时间区间的长度s=0.1天，T=1年，盈余过程样本轨道如图2所示。

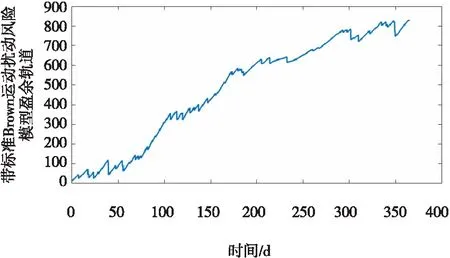
图2 带标准Brown运动扰动风险模型盈余轨道模拟图

对于不同参数σ，由式(5)可计算得到带标准Brown运动扰动风险模型的最终破产概率值。分别进行M=106次模拟，利用Monte-Carlo方法模拟计算5年内的破产概率值，见表2。

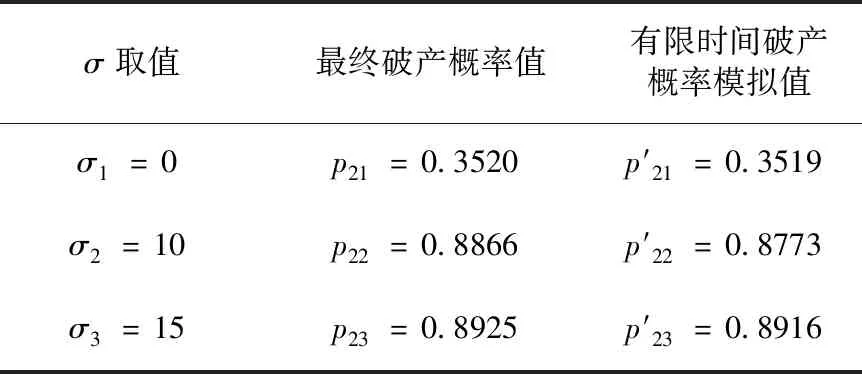
表2 带标准Brown运动扰动风险模型破产概率模拟值

由表2知：(1)有限时间破产概率模拟值接近于最终破产概率值，证明了程序的合理有效性。(2)不同σ的取值对有限时间破产概率模拟数值及最终破产概率值都存在显著影响。

2 实证分析

2.1 模型选取

考虑保险公司办公用品、佣金等其他营业支出对破产概率值的影响，用带漂移项的标准Brown运动刻画其他营业支出及风险干扰，记为W(t)=-μt+σB(t)～N(-μt,σ2t),t≥0。其中非负常数μ表示单位时间的其他营业平均支出，其余符号意义同模型(4)。盈余过程可整合写为如下形式：

(6)

2.2 数据选取

中国太平洋财产保险股份有限公司(简称太平洋财险)成立于2001年11月，注册资本为95亿元。通过《中国保险年鉴2015》[13]和《中国保险年鉴2016》[14]，可得表3和表4中的数据信息(数额单位：百万元，时间间隔单位：天)。

表3 太平洋财险2014年和2015年基本数据信

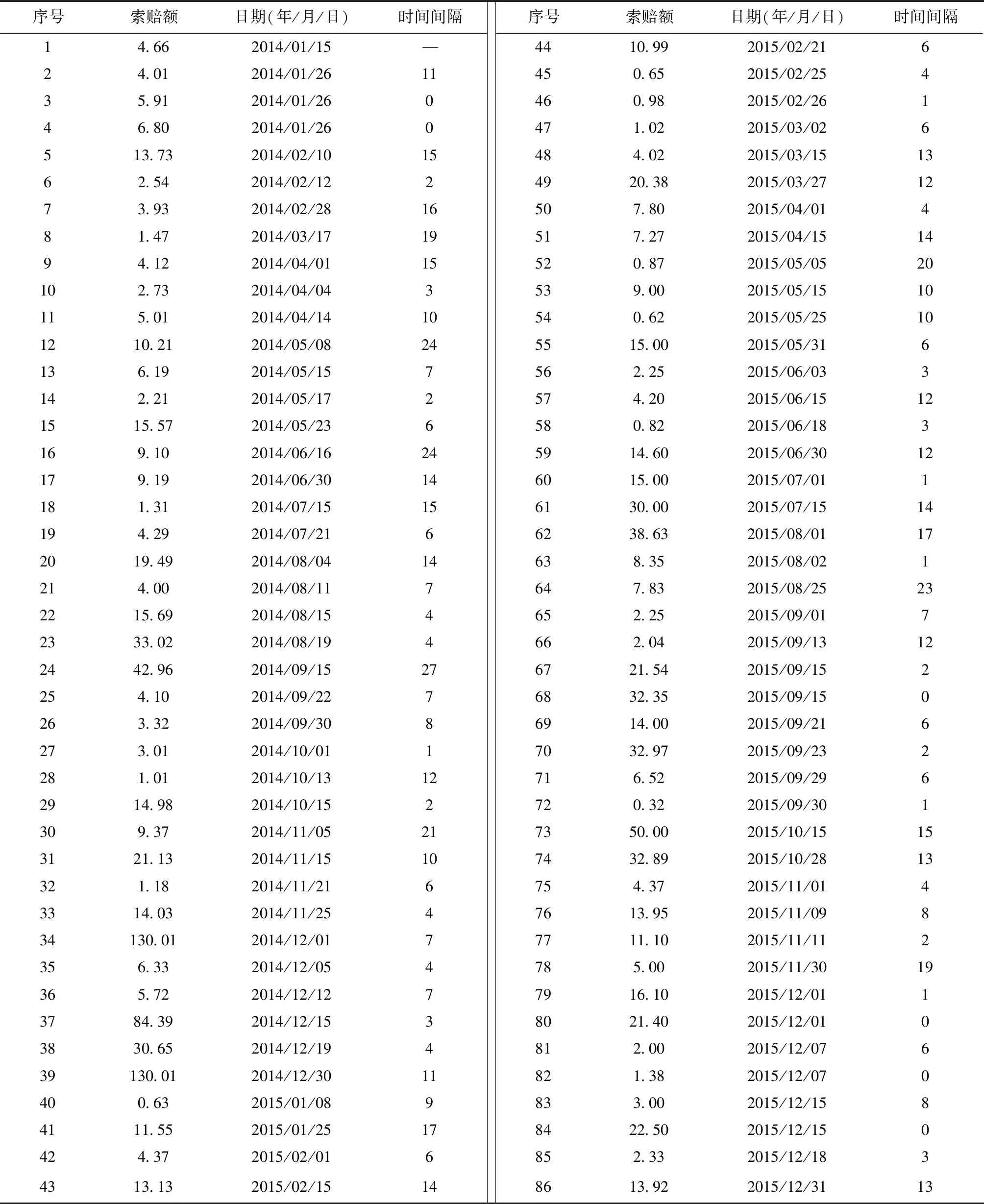
表4 太平洋财险2014年和2015年重大索赔数据

2.3 模型的参数估计及分布检验

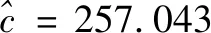
(2) 结合表4中的数据，运用MATLAB R2016a、SPSS 16.0软件进行分析，确定索赔时间间隔序列{Wj,j≥1}和索赔额序列{Xi,i≥1}所服从的分布。

假设索赔时间间隔序列{Wj,j≥1}服从指数分布，运用SPSS 16.0软件进行参数估计，并通过单样本K-S检验来验证这一假设，如图3所示。此检验在显著性水平α=0.05下进行，图3表明渐近显著性(双侧)值大于α，不能拒绝原假设，即{W(t),t≥0}服从均值为μB=9.0886的指数分布。

图3 指数分布K-S检验

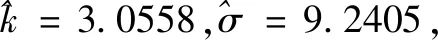
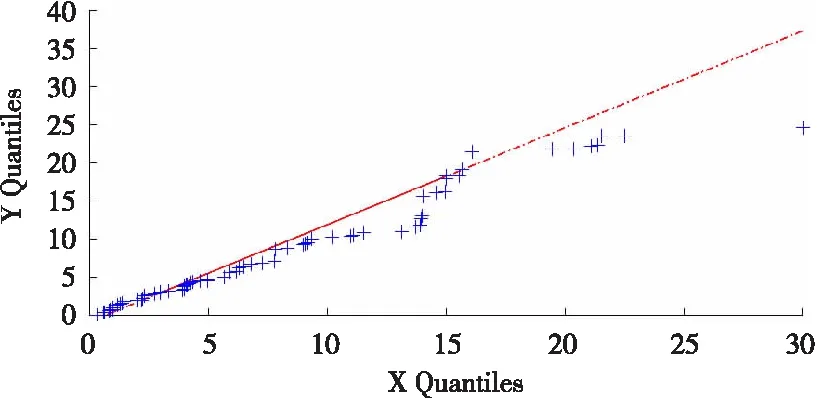
图4 QQ图拟合效果

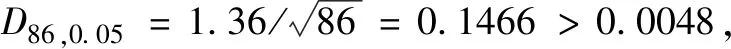
(3) 分别取表3中的2014年初和2015年初的盈余值为初始值，对一年后的盈余值即2014年底和2015年底的盈余值进行计算，相比表3中的真实值U11和U21仍存在偏差，见表5。

表5 太平洋财险2014年和2015年年末盈余值

用扩散扰动项来刻画偏差则εi～N(0,σ2t)，研究期限为一年，即t=365d。根据数理统计中正态总体方差估计方法[15-16]，参数σ的估计式

(7)

2.4 有限时间内破产概率模拟计算

取太平洋财险在2015年年底的总资产为初始盈余即U0=125 011.21百万元，结合2.3节中的参数估计值，取总时间长度T=5年，时间小区间长度s=0.1天，利用MATLAB软件对该公司在2020年底的破产概率进行Monte-Carlo模拟计算，结果见表6。

表6 太平洋财险在2020年底的破产概率模拟值

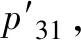
3 结束语

由于带标准Brown运动扰动的重尾索赔风险模型在有限时间内的破产概率及最终破产概率都没有解析表达式，本文针对这一问题提出了一种模拟带标准Brown运动扰动风险模型盈余轨道的有效程序。并结合太平洋财产保险公司实际数据，进一步考虑其他营业支出及风险干扰两大影响因素，利用Monte-Carlo方法对该公司在有限时间内的破产概率进行了数值模拟计算，使得计算结果更加切合实际。