GEE下经验似然估计的渐近正态性质

靳永涛， 尹长明， 吴 迪

(广西大学数学与信息科学学院， 广西 南宁 530004)

引 言

似然是参数模型推断参数时讨论和应用最为重要的概念之一，如最为经典的极大似然估计[1]。经验似然(EL)是Owen[2-3]在Thomas和Grunkemeier[4]提出的非参数似然比问题的想法下的一种非参数统计推断方法。在分布函F未知情况下，参数β(F)的经验似然比统计量在一定条件下收敛到卡方分布并且可以进行假设检验和区间估计等。此后Owen[5]和Kolaczyk等[6]将经验似然方法拓展到线性回归模型和广义线性模型中，比较均值经验似然比估计检验，经验似然的适用范围得以扩大。Qin和Lawless[7]将Owen求经验似然比的限制条件进行修改，提出了一个包含参数信息无偏的限制条件，并给出在满足一定条件下经验似然比统计量的各种性质与Owen的结果一致。Bai等[8-10]对在纵向数据下经验似然方法做了富有成果的研究。Li和Pan[11]提出在不服从独立同分布的纵向数据下将广义估计方程中含参数信息的模型加入求经验似然比的限制条件中，进一步拓展了经验似然方法的适用范围。

上面给出经验似然方法的应用范围和理论支撑，但选取的模型较为简单，同时模型的理论证明条件较强，不易验证。本文在上述作者研究的基础上，分析含有参数信息GEE模型下的经验似然方法，在较易验证的条件下给出经验似然估计存在性、相合性和渐近正态等的理论证明，并运用R语言进行统计模拟。

1 主要结果

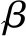
Qin和Lawless[7]的EL模型是在Owen早期EL模型的推广，EL模型如下

(1)

(2)

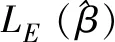
广义估计方程(GEE)是Liang和Zeger[12]在广义线性模型的基础上建立的，它在分析数据的相关性、对重复次数数据的研究，特别是对纵向数据的研究很实用。GEE的一般形式如下：

(3)

(4)

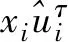
基于经验似然和广义估计方程的介绍，现把求经验似然比最小值(1)式中的g(xi,β)换为式(4)的Si(β)。需要注意这并非简单的替换，因为在GEE中xij是不服从独立同分布的纵向数据，在给出本文主要结果之前，先给出假设条件如下

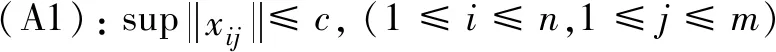
(A3)：Ri(α)≥c，即Ri(α)有正下界;

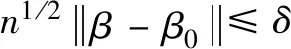
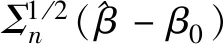
其中

定理1表明经验似然比统计量最小值的存在性问题，即参数β的相合性问题。定理2给出参数β的渐近正态性质。在给出定理证明之前，先给出合适的引理如下：

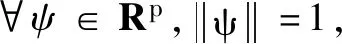
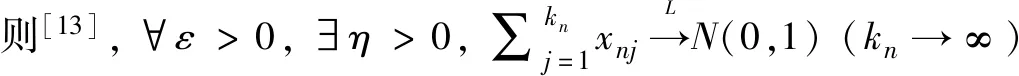
可知要证明

只需要证明

→0 (n→∞)

由条件(A1)-(A5)可知

则引理得证。

引理2[7]在满足(A1)-(A4)的条件下

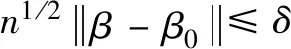
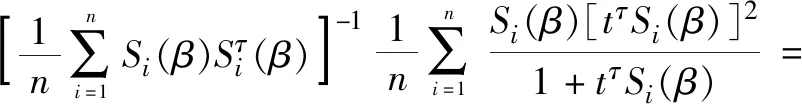
Op(n-1/2)

证明由限制条件可知

上式经化简可得

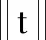
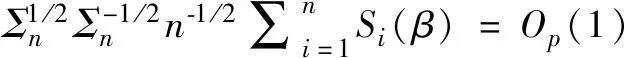
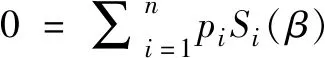
通过逆矩阵的除法得

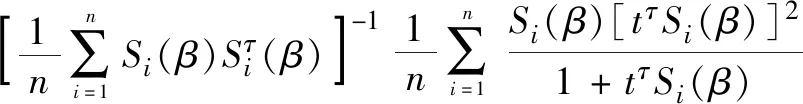
命题得证。

引理4在满足条件A1下有：

(5)

(6)

证明首先证明式(5)，根据已知条件有：

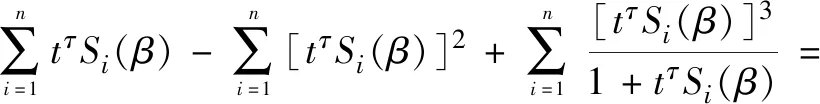
其次证明式(6)如下：

由引理2和引理3可知上式

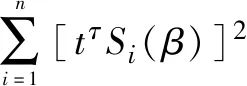
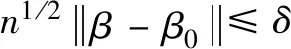
可得：

op(1)

(7)

其中由引理4可知：

将(7)式在β0处运用泰勒展开式有：

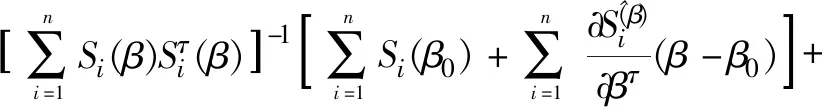
op(1)=

op(1)

上式化简得：

2cδ+δ2]ξ∈(0,tτSi(β))=

(8)

(9)

比较(8)式和(9)式可以发现当n趋于无穷大时，两式中的如下部分：

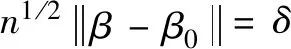
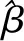
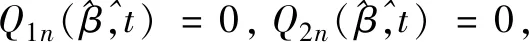
定理2的证明运用引理1的正态收敛性质和定理1的结论可证。首先有：

在不服从独立同分布下运用大数定理有

A22=0

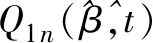
其中

d1=Q1n(β0,0)+op(δn)，d2=op(δn)

运用矩阵求逆可得：

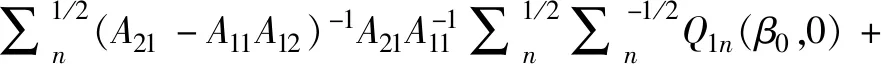
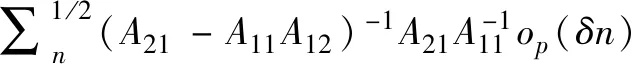
定理得证。

2 统计模拟和结论

例1本例是AnestisTouloumis[17]提到的GEE算法模型与本文EL模型相比较的统计模拟分析，建立模型Pr(Yiτ=1|xiτ)=F(0.5xi)。其中分布F均值为0，方差为π/3。边际分布的工作相关阵R(a)定义如下

运用R语言运行GEE和EL方法的结果见表1和表2。

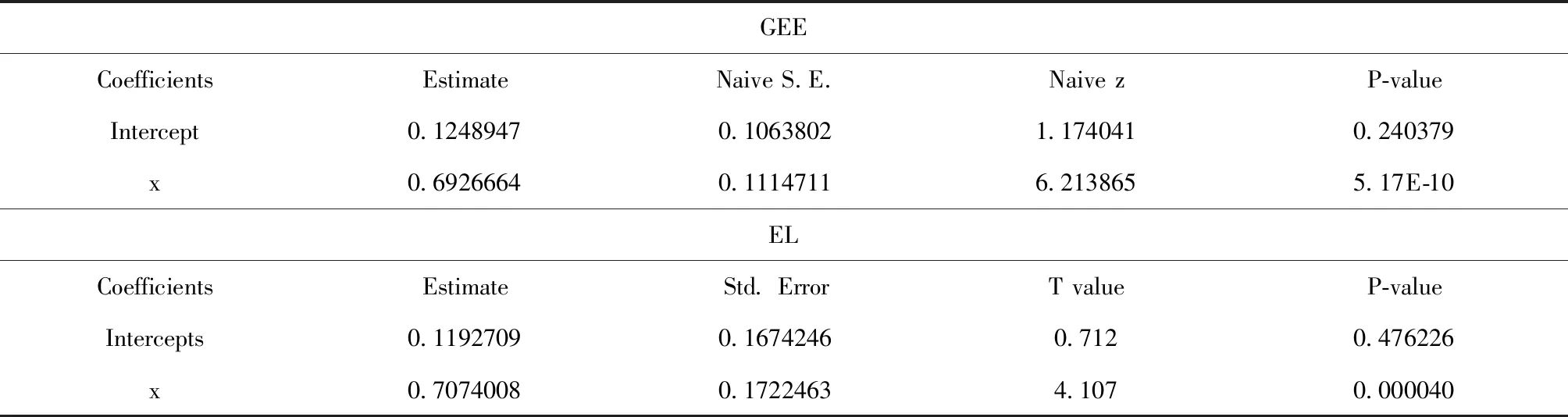
表1 100样本下GEE和EL方法的比较

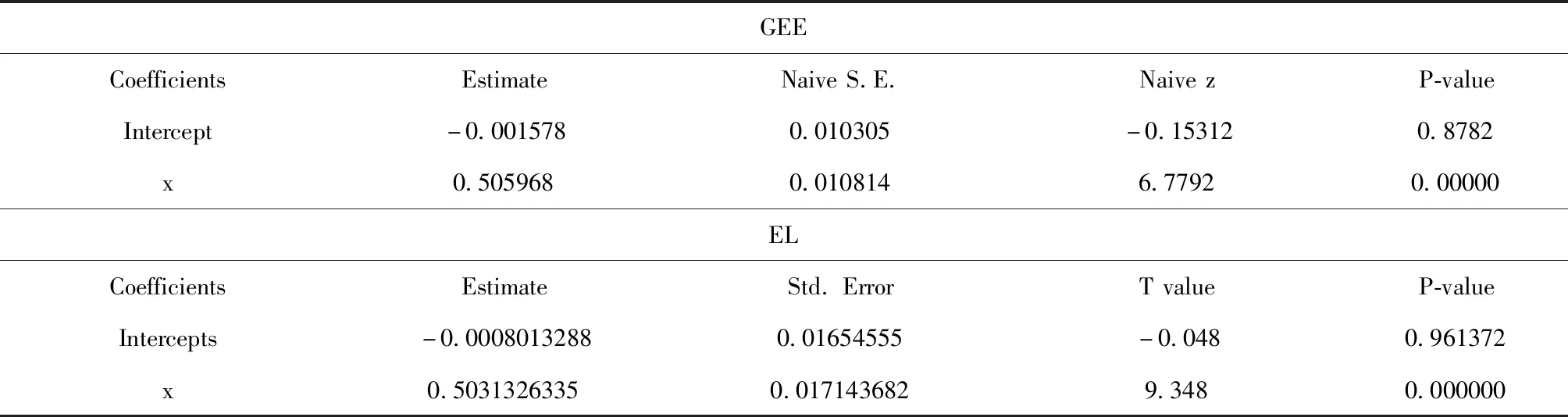
表2 10000样本下GEE和EL方法的比较

表1和表2分别是在100个体和10000个体下GEE和EL方法的运算结果。首先定义个体数量和每个个体观察次数T=4；其次随机产生相应个体100×4的标准正态分布；然后在边际分布工作相关阵的基础上产生高维纵向数据；最后用两种方法进行分析。表中对应的GEE方法用z统计量，经验似然方法用t统计量。当样本量充分大时EL方法较GEE方法x的回归系数更接近0.5，表明EL方法比GEE方法更优。

3 结束语

将GEE和经验似然方法相结合，既保留了GEE方法的误差方差最小的性质，又有经验似然方法构造置信区间域保持性和变换不变性等优点[1-3]。同时在不服从独立同分布和较弱的限制条件下给出经验似然估计存在性、相合性和渐近正态性等的理论证明，有别于经典研究的独立同分布，拓展了经验似然方法在纵向数据下的研究领域，更为精确的给出经验似然方法的适用范围。将来可进一步在理论证明中对约束条件进行弱化[18-21]。此外运用R语言给出统计模拟对理论证明进行补充，对比GEE方法结果表明纵向数据下经验似然方法更优，对于纵向数据在实际应用中有较好的参考价值。