基于双孔隙径向复合地层渗流理论的气井产能模型
2019-02-27欧家强陶小红蔡珺君
袁 权, 欧家强, 颜 平, 陶小红, 杨 琛, 蔡珺君, 邓 庄
(1.中国石油西南油气田公司川中油气矿, 四川 遂宁 629000;2.成都理工大学能源学院, 成都 610059)
引 言
气井的产能是气田开发工作者最为关心的问题之一,它是气井配产的重要依据,是油气井生产系统分析及生产动态预测的基础[1-2]。目前,气层储层产能评价方法[3-6]主要有基于测井的产能评价方法,基于地震的产能评价方法,及基于试井的产能评价方法等。其中,最准确的是通过产能试井来评价气井产能。由于压力恢复试井可以准确测试地层的参数,越来越多的研究人员开始研究如何利用压力恢复试井结果,并基于渗流方程构建产能方程,进而计算气井产能。唐洪俊等人提出了应用不稳定试井资料确定气井产能的方法[7-8];李治平等推导了在近井区存在非达西渗流的情况下的复合气藏的产能方程[9];在生产井的井控区,近井和远井地带(内区和外区)储层物性不同,朱黎鹞等在单一介质储层的渗流方程基础上,建立了径向复合气藏二项式产能方程[10-11]。
四川盆地大多数碳酸盐岩气藏属于裂缝-孔隙型气藏。各气井的单井控制区域径向内,地层渗透率存在着较大的差异。在正式投产前,一般还要进行增产改造。因此,在径向上将形成存在明显物性差异的非均质区域。传统的基于单一介质储层的径向均质复合产能计算公式与气藏实际情况不相符。在双孔隙介质储层的渗流方程基础上推导出的产能公式更符合实际地质特征。
本文首先推导出双孔隙径向复合气藏气井二项式产能表达式, 利用不稳定试井解释资料获得双孔隙径向复合气藏内、外区的各项参数后, 得到径向复合气藏气井二项式产能方程和无阻流量。
1 双孔隙径向复合气井的产能方程推导
首先采用双孔隙介质模型,建立拟稳态产能方程。
1.1 双孔隙模型的气井拟稳态产能方程
假定在圆形地层中心的一口直井,储层厚度为h且全部射开,原始压力为Pi,直井半径为rw。假定气井定产量Qsc生产,外边界定压Pe,如图1所示。
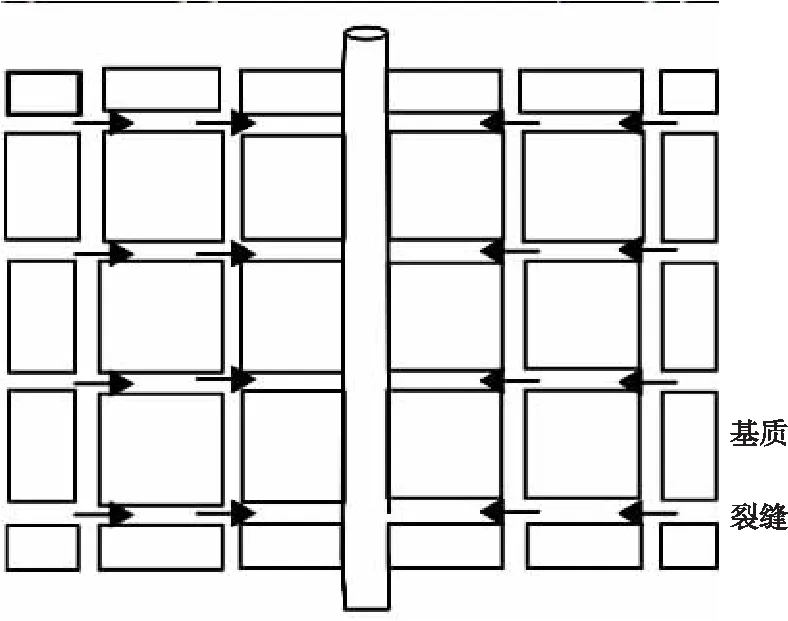
图1 双孔渗流模型
定义拟压力函数[12]:
(1)
式中:P为压力,MPa;μ为气体粘度,mPa·s;Z为天然气偏差因子,无因次。
对于裂缝孔隙型储层,在裂缝中渗流属于高速非达西渗流,因此采用Forcheheimer二项式公式来表征[13]:
(2)
式中:β为非达西渗流系数[14],1/m;K为渗透率,mD;v为流体速度,m/s。
碳酸盐岩和砂岩非达西渗流系数不同,根据非达西渗流系数与渗透率拟合归纳出的震旦系灯影组碳酸盐岩非达西系数表达式为:
裂缝运动方程为:
(3)
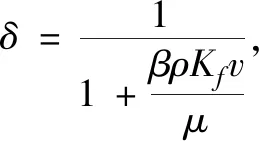
可得到裂缝渗流速度为:
(4)
将非达西流动、渗流速度和气体密度代入裂缝压力梯度公式,得:
(5)
式中:Qsc为地面标准状态下气井产量,m3/d;Tsc为标准状态下温度,K;Psc为标准状态下压力,MPa;ρgsc为标准状态下的气体密度,kg/m3;T为气藏温度,K;h为储层厚度,m。
平面径向流裂缝和基质连续性方程分别为:
(6)
(7)
式中:v为流体速度,m/s;φ为孔隙度,小数;ρg为标准状态下的气体密度,kg/m3;f、m为下标,其中f表示裂缝,m表示基质。
考虑基质和裂缝的状态方程分别为
(8)
式中:φ0为初始状态的孔隙度,小数;Cφf为裂缝的压缩系数,1/MPa;Cφm为基质孔隙的压缩系数,1/MPa。
基质向裂缝的窜流项为:
(9)
式中:α为双孔隙形状因子,无因次。
将运动方程、窜流项都代入到连续性方程,得:
(10)
(11)
得到二项产能公式为:
(12)
(13)
式中:re为井控区半径,m。
(14)
(15)
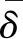
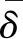
(16)
(17)
式中:ω为储容比,可从压力恢复试井解释结果中读取。
(18)
(19)
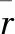
如果考虑表皮效应[15],得到系数:
(20)
式中:S为表皮系数,可从压力恢复试井解释结果中读取。
无阻流量计算公式:
(21)
2.2 双孔隙径向复合地层的气井拟稳态产能
双孔隙径向复合气藏[16-18]平面、剖面示意图分别如图2、图3所示,径向渗流区域被分割成近井区渗流区和远井区渗流区。利用2.1节中双孔隙模型的气井拟稳态产能公式,可分别得到双孔隙径向复合地层拟稳态近井区和远井区产能方程。由于两个渗流区域在边界上是连续的,联立求解,即可得到双孔隙径向复合地层拟稳态产能方程。
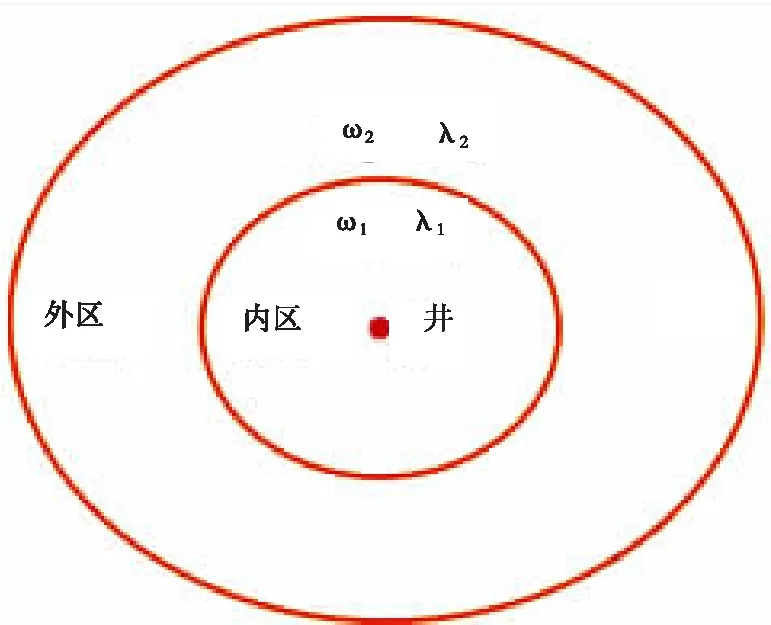
图2 基于双孔隙基质的径向复合地层平面示意图
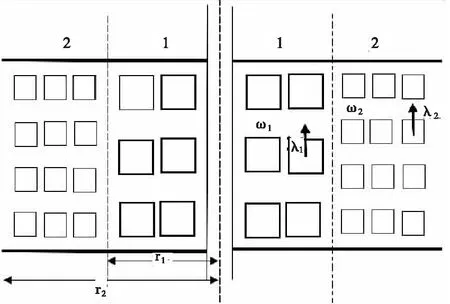
图3 基于双孔隙基质的径向复合地层剖面示意图
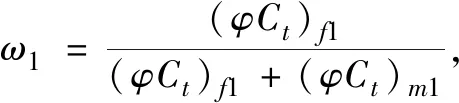
在内区,可以得到:
(22)
在外区,可以得到:
(23)
式(22)与式(23)相加,得到双孔隙径向复合产能方程:
(24)
无阻流量计算公式:
(25)
其中:A=A1+A2,B=B1+B2。
(26)
(27)
(28)
(29)
(30)
(31)
(32)
式(25)~式(32)各式中的下标1、2含义:1表示内区,2表示外区。
利用径向压力公式,计算内区、外区边界压力:
(33)
然后求算术平均压力,内区、外区的平均压力为:
(34)
计算内、外平均半径公式为:
(35)
2 实例分析
灯影组气藏M井,生产层位为灯四段,储层产层中部垂深5297.3 m,目前地层压力Pi取为58.04 MPa,储层平均孔隙度φ=3.8%,岩石压缩系数为Cφ=0.002 MPa-1。标准状态温度Tsc=293.15 K,标准状态压力Psc=0.101 MPa,井底温度T=152.62 ℃(425.77 K),井口温度40.3 ℃,储层有效厚度28.1 m,井半径rw=0.044 m。
M井储层的测井解释结果如下:储层发育层位灯四,常规测井资料指示孔隙发育,电成像资料指示溶蚀孔洞非常发育,裂缝发育,阵列声波能量衰减明显,核磁共振指示孔隙结构以中小孔为主。测井解释符合双孔隙径向复合模型特征。
双孔隙径向复合模型,其曲线特征如图4所示,主要有以下三点:
①在近井带渗流过程中,观察到一个典型的双孔类型储层的渗流特征,即:基质与裂缝的窜流段在导数上表现为“谷”。该段试井曲线解释的渗透率和储容比等裂缝参数是压裂改造区的性质。
②如果远井地带的物性变差,导数曲线整体呈上升趋势。反之,如果远井地带的物性变好,导数曲线整体呈下降趋势。
③在近井带渗流过程中,也能观察到一个典型的双孔类型储层的渗流特征。该段试井曲线解释的渗透率和储容比等裂缝参数是地层本身的性质。
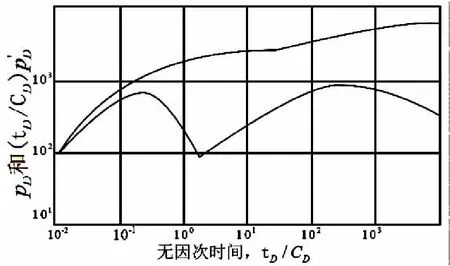
图4 双孔隙径向复合地层试井曲线形态示意图
M井于2017年8月12日开始进行井下压力恢复测试,8月22日压力测试结束,其双对数曲线如图5所示。
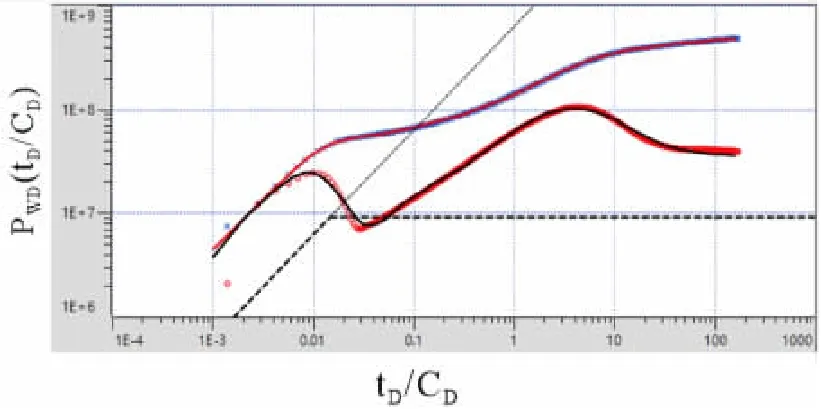
图5 M井压恢双对数拟合图
结合磨溪108井的储层类型,参考双孔径向复合试井模型的特征,试井解释模型选择双孔径向复合模型,见表1。
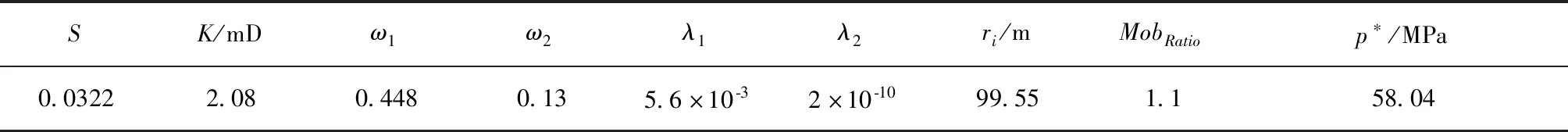
表1 M井双孔隙压力恢复试井解释结果
在表1中:表皮系数S=0.0322,内区半径为r1=99.55 m,内区裂缝渗透率为Kf1i= 2.08 mD,外区半径为re=690.34 m,外区裂缝渗透率为Kf2i=1.89 mD,双孔隙形状因子为α=0.6。
由气体组分分析结果,计算临界参数得到:拟临界温度192.8241 K,拟临界压力4.8458 MPa。
首先采用双孔隙径向复合模型,将算术平均压力、内区半径、外区半径、内区紊流系数、外区紊流系数,代入参数计算公式,得到计算的系数见表2。

表2 M井双孔隙产能公式参数
计算得到:
A=A1+A2=73.814
B=B1+B2=23.1634
代入无阻流量计算公式:
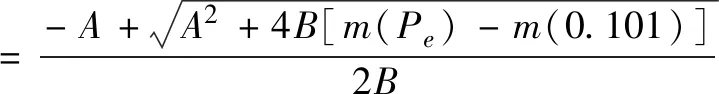
=75.40×104m3/d
将本文计算结果与气井产能试井结果进行对比,见表3。

表3 不同方法产能计算结果对比
从表3中可以发现,基于压力恢复试井参数常能方程计算的产能结果,比常规一点法产能计算结果更为准确,有较好的适用性。
3 结 论
(1)基于渗流力学理论,采用压力恢复试井结果,可以建立双孔隙径向复合地层的气井产能公式。
(2)本文提出的用压力恢复试井资料确定气井产能的方法较气井产能试井提高了经济效益和工作效率,扩大了压力恢复曲线的应用范围。
(3)对比产能试井和常规一点法结果,发现该公式有较高的准确性,适用于进行过压力恢复试井但未进行产能试井且试井解释模型为双孔隙径向复合的气井。
