动态加载率对巷道内裂纹扩展速度及动态起裂韧度的影响
2019-02-22朱哲明董玉清
周 磊, 朱哲明, 董玉清, 应 鹏, 王 磊
(四川大学 建筑与环境学院 深地科学与工程教育部重点实验室, 成都 610065)
地下岩体结构时常承受动载荷的作用,如爆破、顶板破裂、冲击地压等,对地下岩体结构稳定性具有严重影响,造成的地质灾害也越来越严重。在既有巷道围岩中存在大量裂纹缺陷,如天然节理、孔洞、裂隙等,当冲击地压等瞬时动态载荷发生于采矿掘进过程中时,冲击应力波特别容易诱发既有围岩裂纹的起裂、扩展,与周边裂纹缺陷贯穿,降低围岩强度,随后促使巷道的破坏。巷道内裂纹缺陷在动态载荷作用下,裂纹扩展速度、动态断裂韧度与动态加载率有很大的关系,因此研究不同冲击载荷作用下巷道内裂纹的扩展速度及动态断裂参数具有较大的实践意义。
动荷载作用下巷道的稳定性已经得到了很多国内外研究学者的关注,而动态载荷作用下,巷道内裂纹的扩展速度测试及动态断裂韧度计算是研究课题的重点之一,特别是在不同巷道围岩的岩石介质工况下,裂纹扩展的速度也将有很大的差别。郭东明等[1-2]研究了爆炸载荷作用下巷道内裂纹的扩展行为,对裂纹尖端起裂前动态应力强度因子的演化规律进行了分析。唐治等[3]建立了冲击地压巷道围岩支护作用的动力学模型,分析了支护结构对巷道在冲击载荷作用下的围岩加强作用。倪海敏等[4]基于内蒙古唐公沟巷道工作面的围岩情况,采用损伤模型及经典的Drucker-prager准则对巷道在冲击载荷作用下动态稳定性进行了数值分析。Wang等[5-6]采用裂纹扩展计监测了侧开单裂纹半孔板中裂纹的扩展速度,并结合高速摄影机监测到了裂纹止裂现象的存在。Wang等[7-9]采用应变计与裂纹扩展计相结合的方式研究了动态加载率对平台巴西圆盘动态起裂韧度的影响。Wang等[10]以落锤冲击试验并结合应变片测试了VB-SCSC试件的裂纹扩展速度,并分析了冲击载荷作用下入射波与反射波对裂纹快速扩展过程的影响。
随着分离式霍普金森压杆(Split Hopkinson Pressure Bar,SHPB)试验装置的发展与改进,SHPB试验装置对于岩石类等各种脆性材料在动态载荷作用下的研究已经较多。Zhang等[11-12]利用SHPB试验装置并结合裂纹断裂计测试了半巴西圆盘试件的动态起裂韧度,并指出高速摄影系统仅仅适用于准静态相关试验的分析。Chen等[13-14]采用SHPB试验装置与应变片测试了半巴西圆盘的动态断裂韧度,并对裂纹尖端的动态断裂韧度各种测试方法进行了分析与讨论。但由于SHPB试验装置对于试件尺寸大小的局限性,针对较大的巷道模型试件不能使用,因此,基于SHPB试验装置原理的各种落锤冲击试验机就孕育而生。宋义敏等[15-16]采用自发研制的落锤冲击试验机结合高速摄影机搭建的数据采集系统对花岗岩内Ⅰ型裂纹在冲击载荷作用下的裂纹扩展速度、动态断裂全过程中的裂尖应力强度因子等进行了定量分析。潘峰等[17]采用落锤冲击试验系统研究了不同加载率作用下特殊设计三点弯曲梁的破坏形态并进行相应的理论分析,指出岩石、混凝土类不均匀脆性材料动态强度提高的主要原因是材料的不均匀性和惯性效应联合作用。
本文基于SHPB试验装置原理装配成落锤冲击试验机,对青砂岩制作的巷道模型试样进行中低速冲击加载,随后结合裂纹扩展计对巷道内裂纹的起裂时间及裂纹在围岩中的快速扩展特性进行研究,并采用ABAQUS程序结合试验-数值法对裂纹在不同加载率作用下的动态起裂韧度进行计算,并对巷道内裂纹断裂参数进行分析,得出巷道围岩内裂纹的扩展特性,为提高巷道结构的动态稳定性提供一定的理论基础。
1 试验过程
1.1 试验装置
试验装置使用基于SHPB原理并能实现中低速冲击载荷加载的落锤冲击试验机,入射板长li=3 m,透射板lt=2 m,板宽H=0.3 m,板厚B=0.03 m,如图1所示。经过与SHPB试验装置杆件材料对比,入射板与透射板选择弹性材料 LY12CZ 铝合金,该材料的力学性质参数,如表1所示。为了减小应力波传播过程中的弥散效应,在落锤与入射板之间粘贴一块黄铜片作为整形器,该措施也能够很好地延长半正弦波的加载时间。为了减小试件与入射板、透射板之间的摩擦效应,在巷道模型试件与入射板、透射板之间涂抹少量黄油。落锤的冲击高度采用光电测速装置进行测试,冲击高度范围可达0~10 m,试验采用冲击高度h=1.5~3.5 m。
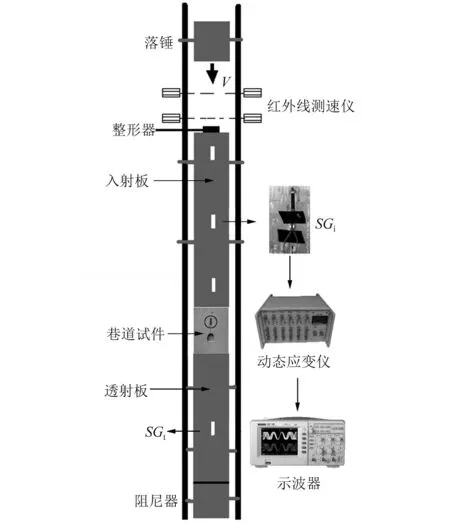
图1 冲击加载装置Fig.1 Impact loading device

材料ρ/(kg·m-3)σc/MPaσt/MPaKIC/(MPa·m1/2)E/GPaνCd/(m·s-1)Cs/(m·s-1)CR/(m·s-1)LY12CZ2 85071.70.35 006Sandstone2 26522.081.080.46815.90.182 5631 607.41 457.6
1.2 试验试件
鉴于巷道断面对巷道围岩稳定性的影响,圆弧拱巷道围岩的稳定性远大于矩形巷道,本文选择圆弧拱矢跨比为0.5的巷道模型作为研究对象,这样既可以显著改善巷道围岩的稳定性,减少巷道围岩的变形,也可以充分的观测巷道内裂纹对巷道围岩稳定性的影响,更可以很好地测试裂纹在围岩中快速扩展的问题,避免矩形断面拐角处等应力集中现象对测试结果的影响[18-20]。假设某地下深部煤矿开采巷道宽度5 m,高度6 m,圆弧半径2.5 m,矢跨比为0.5,按此尺寸比例进行相似比例缩小设置,巷道断面宽度w=50 mm,巷道侧帮高L=35 mm,巷道半径r=25 mm,如图2(a)所示。为了准确地测试裂纹的扩展速度及吻合裂纹扩展计的测试方法,加工裂纹扩展路径为相对直线特性的纯Ⅰ型预制裂纹,因此在巷道对称轴中轴线上设置预制单裂纹。经过ABAQUS对巷道模型构件进行准静态计算可知,当裂纹位于巷道拱顶位置时,KⅡ/KⅠ≈0, 表明KⅡ值很小,此时为纯Ⅰ型裂纹。 裂纹长度a=50 mm, 与巷道的跨度w比值为1∶1, 巷道模型试件,如图2(b)所示。该巷道模型能够很好的表观在静态载荷作用下的断裂行为,模型试件大小为300 mm×350 mm×30 mm。巷道模型的加工采用水刀进行切割,切割试件的精度介于0.1~0.25 mm。试件成型之后,采用多功能角磨机对巷道模型试件周边进行打磨抛光处理,使得试件的长宽高误差在±1 mm之内。裂纹采用0.5 mm厚的拉花锯条进行加工处理,随后裂纹尖端采用0.1 mm厚的美工刀片进行锐化处理,使得裂纹尖端的应力集中现象更为准确。总共制作20组模型试件进行试验测试,避免动态加载试验过程中偶然因素等误差因素对试验结果的影响。模型材料选择为青砂岩,将巷道模型试件理想化为均匀的连续介质力学模型,这样既能够避免裂纹扩展路径超出裂纹扩展计的监测范围,也能够很好地测试砂岩围岩中裂纹的扩展速度。该砂岩的物理性质参数经过某地质勘察设计院的SonicViewer-SX岩样超声波波速测试仪器的测试结果,如表1所示。
1.3 加载波形
为了采集到落锤加载过程中的半正弦脉冲信号,数据采集系统依据SHPB试验装置进行设置。首先在入射板上贴有3张应变片(BX120-50AA)分别记为SG1,SG2,SG3, 它们距离试件上端面的距离分别为l1=0.5 m,l2=1.5 m,l3=2.5 m,经过最终的试验数据分析选择SG1(l1=0.5 m)作为入射板脉冲信号的数据采集点;在透射板中间处粘贴一张应变片(BX120-50AA)作为透射端的脉冲信号采集,记为SGt。将应变片的应变信号经过超动态应变仪放大转换成电压信号,最后用瞬态记录仪进行数据的采集,冲击高度h=2.508 m的加载脉冲信号,如图3所示。从图3可知,这与SHPB试验装置所获的加载脉冲信号相似,这也说明该试验装置能够很好地实现中低速冲击载荷作用下岩石材料的动态断裂试验[21-23]。
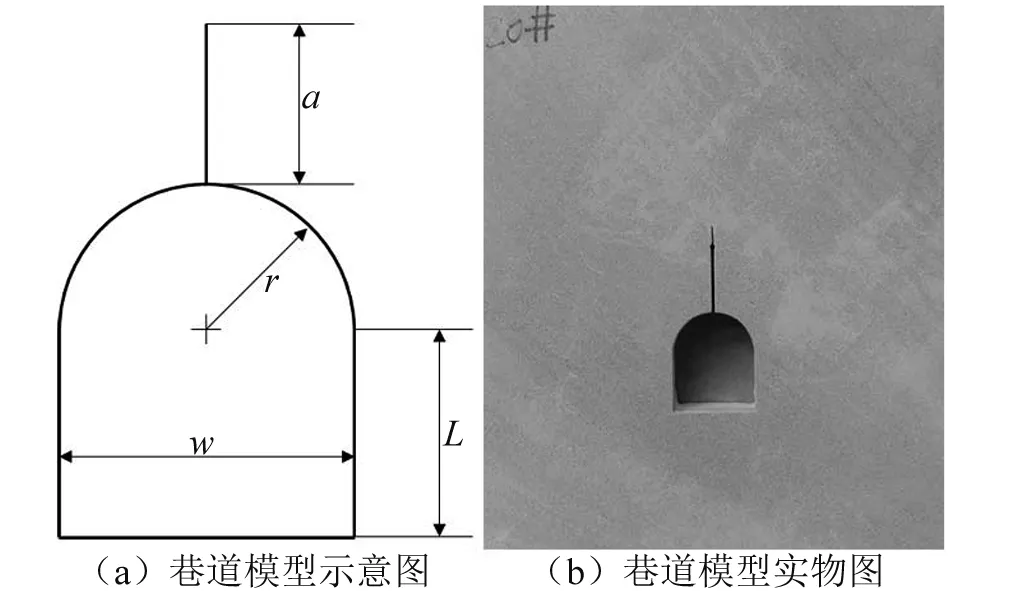
图2 巷道模型试件尺寸示意图Fig.2 Sketch map of tunnel model
根据SHPB试验技术,基于一维应力波传播理论假设,将入射板上的入射波与反射波信号进行叠加可以得到入射板上的作用力Pi(t),由透射波信号可以计算得到透射板上的作用力Pt(t),计算式为[24]
(1)
式中:E为弹性杆件的弹性模量;εi(t),εr(t),εt(t)分别为入射板上的入射波应变时程曲线和反射波应变时程曲线及透射板上的透射波应变时程曲线。最终经过数据转换获得入射端与透射端的加载应力时程曲线。
为了研究动态加载率对巷道内预制裂纹起裂时间ti及起裂韧度的影响,本文将动态加载高度h所得的应力曲线与动态加载率进行相应的转换,对入射板上的入射波与反射波进行叠加,得到应力曲线,如图4所示。随后对入射载荷Pi(t)上升沿进行线性求导,得到上升沿斜率值即为动态加载率[25]。从图4可知,动态加载高度h=2.508 m的动态加载率为257.898 GPa/s,最大应力值为25.798 MPa。
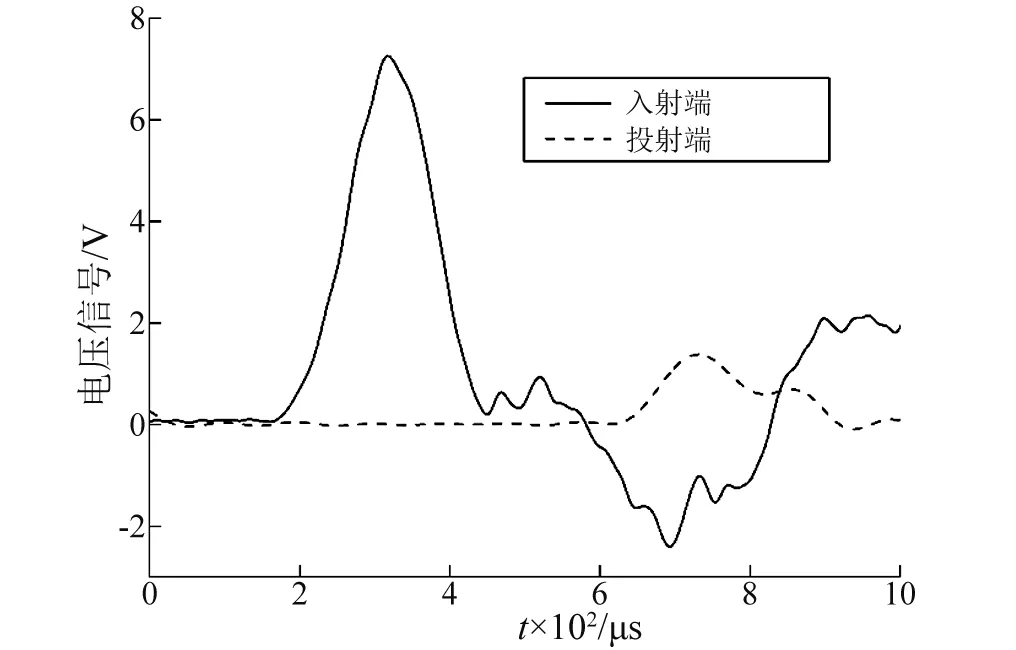
图3 加载高度h=2.508 m的脉冲波形Fig.3 Loading waveform of h=2.508 m
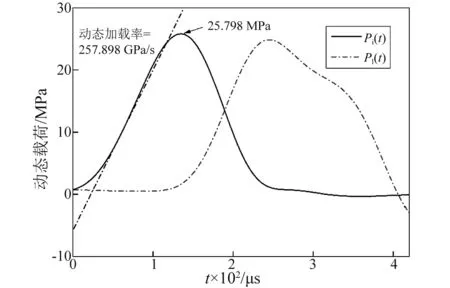
图4 动态加载载荷与动态加载率Fig.4 Dynamic loading force and dynamic loading rate
2 裂纹扩展计的使用
为了精确地测试巷道内预制裂纹的扩展速度,在裂纹尖端粘贴由玻璃丝布基底与金属敏感栅丝组成的裂纹扩展计(Crack Propagation Gauge,CPG),敏感栅丝的间距及长度可以根据试验测试要求进行定制。在粘贴CPG的过程中,使CPG的第1根金属栅丝与裂尖重合,且使CPG 的长度方向平行于裂纹预期扩展方向,使裂纹预期扩展路径尽量垂直通过各栅丝的中点处,并且最接近裂纹尖端的栅丝R1电阻最小,距离裂纹尖端最远的栅丝R10电阻最大。这样既能够很好地测试裂纹的起裂时间,也能够很好地测试裂纹的快速扩展过程。本文选择由10根等长但宽度不同因而电阻不同的金属栅丝并联而成的CPG进行试验测试,栅丝之间的间距l0=1.1 mm,初始电阻约为3 Ω,宽度为h0=10 mm, 总长度l=9.9 mm,如图5所示。
首先,测试系统在CPG两端并联电阻R1=51 Ω,随后与电阻R2=51 Ω串联,最后与恒压源连接,恒压源能够提供0~60 V稳定电压,调压精度能够达到0.1 mV。这些措施既能够使CPG两端的电压足够大,充分采集到CPG两端电压的变化,又能够防止CPG两端电压过大导致CPG超过其额定功率损坏,测试电路(见图5)。
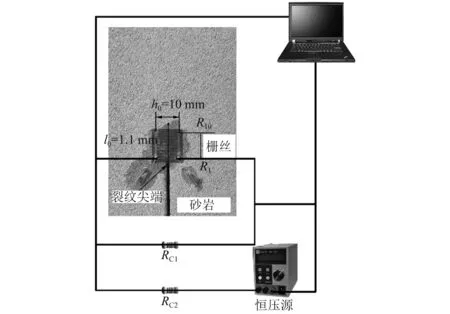
图5 CPG测试系统Fig.5 CPG test system
2.1 CPG试验数据
当裂纹开始起裂时,CPG的10根敏感栅丝一根根被拉断,在拉断的过程伴随着电阻的变化,因而CPG两端产生电压变化,形成阶梯电压信号,如图6(a)和图6(b)所示。并将每1个电压信号进行求导绘制于图中,可以在导数的极值点确定为每1根金属栅丝的断裂时刻,再根据每2根栅丝的断裂时间差及栅丝之间的距离l0就可以求得裂纹向前的扩展速度。选择加载高度h1=3.506 m和h2=2.834 m两种试验数据进行分析,如图6(c)和图6(d)所示。在CPG粘贴时,第1根栅丝与裂纹尖端重合,即第1根栅丝断裂时就可以作为预制裂纹的起裂时刻ti。在不同的加载高度情况下,裂纹的起裂时刻ti1与ti2有所不同。裂纹的扩展速度随着裂纹扩展距离的增加,裂纹扩展速度在逐渐的波动,不是一个定值;加载高度h1的平均扩展速度va1=l/(ts1-ti1)=630.573 m/s,加载高度h2的平均扩展速度va2=l/(ts2-ti2)=596.385 m/s,表明加载高度h对裂纹扩展速度有一定的影响。
2.2 加载高度h对裂纹扩展速度的影响
为了分析动态加载高度h对巷道内裂纹扩展速度的具体影响程度,将20组巷道模型试件CPG测定的裂纹扩展速度进行计算。由于试验加载过程中偶然因素的影响,例如预制裂纹的扩展路径偏出CPG监测范围,有5组巷道模型试件没有监测到试验数据,因此仅对15组试验数据进行分析,得到裂纹扩展速度与加载高度h的曲线图,如图7所示。曲线进行相应的二次拟合,拟合函数在图中列出,拟合相关系数为0.955 8。从图7可知,动态加载高度h=2.834 m,裂纹扩展速度为596.385 m/s;动态加载高度h=3.002 m,裂纹扩展速度为630.573 m/s。裂纹扩展速度随动态加载高度增加而增加,随后增加趋势逐渐变缓。当动态加载高度达到一定程度时,裂纹的扩展速度不再增加,将趋于稳定,即裂纹扩展速度有一个极限值,极限值略小于0.38C0=988.435 m/s(C0为砂岩纵波波速)[26]。
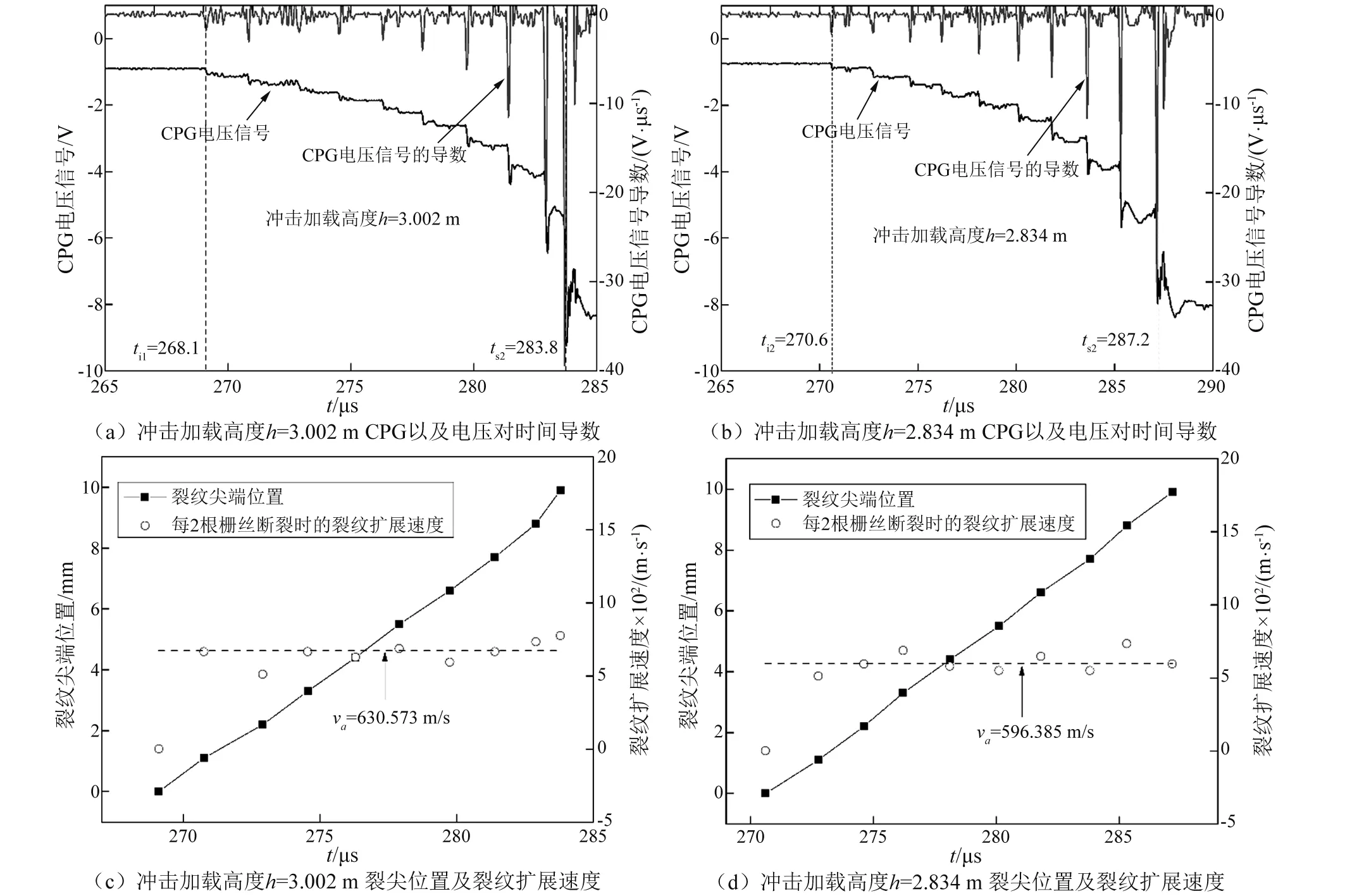
图6 CPG记录的电压信号及每2根栅丝断裂时的裂纹扩展速度Fig.6 Voltage signal curves by CPG and crack propagation speed between 2 fine wires
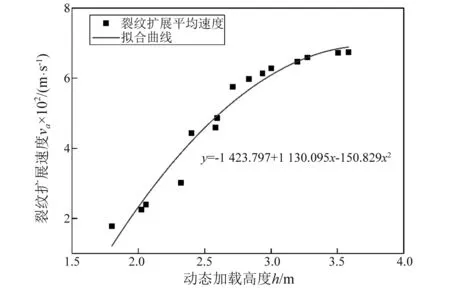
图7 不同加载高度h下的平均裂纹扩展速度Fig.7 Average crack propagation speed under different loading heights h
3 动态加载率的影响
3.1 动态加载率与起裂时间的关系
为了分析不同动态加载率作用下巷道预制裂纹起裂时间的变化,得到起裂时间与动态加载率的关系曲线,如图8所示。曲线进行相应的二次拟合,拟合函数在图中列出,拟合相关系数为0.849 9。从图中可以看出裂纹的起裂时间随着动态加载率的增加逐渐降低,降低幅度范围约大概在50 μs以内。随着动态加载率的增加,起裂时间呈缓慢下降的趋势,并在较高动态加载率情况下出现较大的波动现象。当动态加载率为202.163 GPa/s时,起裂时间为307 μs;当动态加载率为357.881 GPa/s时,起裂时间为257 μs。在较低动态应变率的情况下,围岩的变形仅仅只有一部分微裂纹,而随着动态加载率的增加,越来越多的微观裂纹参与岩石变形,直至达到某一动态加载率的峰值,所有的微观裂纹都参与动态断裂变形,且在这一峰值点后,动态起裂时间在某一值上下波动。微裂纹越多,达到裂纹起裂所需的时间越短[27]。
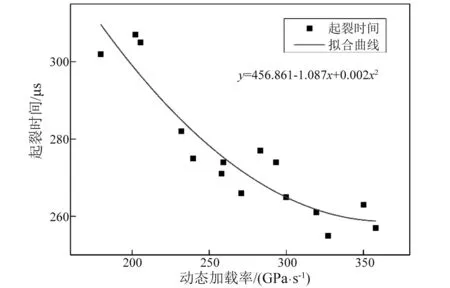
图8 起裂时间与动态加载率Fig.8 Dynamic initiation time and loading rate
3.2 起裂韧度的计算
巷道内裂纹在冲击载荷作用下,由于惯性力效应形成的应力波作用不能忽视,从而动态起裂韧度与静态起裂韧度有明显的不同。裂纹的起裂是由众多的微观裂纹连续聚集而成的过程,而裂尖微观裂纹的生成分布及数量是由应力强度因子及材料本身性质决定的。从试样受动态载荷作用到裂纹起裂前,动态应力强度因子逐渐增加,预制裂纹将发生微裂纹的聚集,当应力强度因子增加到动态起裂韧度时,裂纹微裂纹的数量将达到峰值,在微裂纹的相互作用下,最终将形成宏观裂纹的起裂与扩展,因此计算冲击载荷作用的动态起裂韧度就变得尤为重要。
为了计算巷道模型试件在冲击载荷作用下的动态起裂韧度,依据CPG测算的裂纹起裂时刻ti与动态加载应力曲线共同确定裂纹的起裂韧度,采用试验-数值法进行计算,此种方法已经被较多的国内外学者进行起裂韧度、扩展韧度等断裂参数的计算。
首先,本文采用ABAQUS有限元程序进行动态应力强度因子曲线的计算,随后结合CPG测试的起裂时刻ti确定巷道内裂纹的动态起裂韧度。为了验证ABAQUS动态有限元数值方法的有效性,Chen[28]对经典问题之一的中心板裂纹受Heaviside阶跃函数载荷进行有限元数值模拟,有限元差分法计算结果与ABAQUS动态数值分析结果在定性及定量方面基本吻合,这也与解德等[29]数值分析结论基本一致,表明ABAQUS程序能够很好地计算动态载荷作用下的应力强度因子时程曲线。
本文采用动态隐式模块(ABAQUS/Standard)进行巷道模型试件裂纹尖端应力强度因子的计算,基于图2的模型尺寸建立15组相应的二维数值有限元模型,裂纹尖端区域采用6节点的三角形CPS6网格单元,其余区域采用8节点的四边形CPS8单元,总共包含5 481个网格单元,16 732个单元节点。边界条件设置将图4中的入射端载荷Pi(t)与透射端载荷Pt(t)分别加载至巷道模型试件的上下两端。最后在巷道数值模型中设置相应的重力载荷,考虑重力载荷对巷道模型的影响,数值模型如图9所示。荷载加载步设置600个步长,每一步长间隔时间为1 μs。砂岩物理性质参数设置的实测参数进行相关设置,如表1所示。
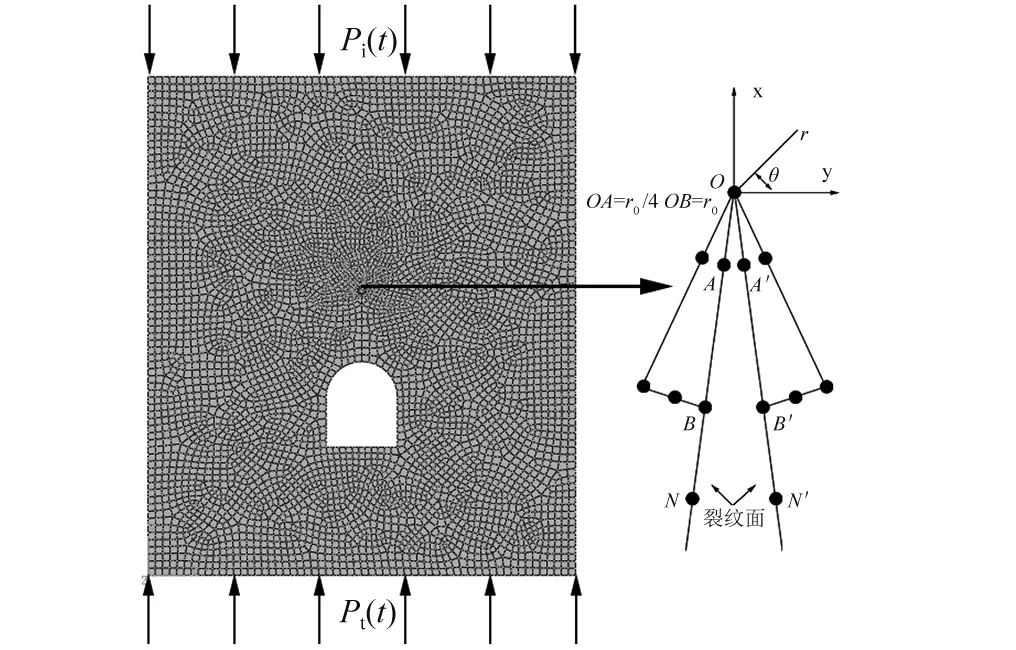
图9 数值模型示意图Fig.9 Sketch map of numerical model
通过ABAQUS获得的动态加载高度h=2.508 m的动态应力强度因子时程曲线,如图10所示。从图10可知,裂纹尖端在开始受到动态载荷作用下出现大概时间约为150 μs的压应力阶段,随后裂纹尖端应力强度因子进入拉应力阶段,结合CPG测定的起裂时刻ti=271 μs,可以确定出巷道模型试件内预制裂纹的起裂韧度为1.351 MPa·m1/2,而在裂纹的起裂后,裂纹尖端的应力强度因子继续增大,达到峰值2.131 MPa·m1/2后逐渐减小,裂纹尖端的起裂韧度小于动态应力强度因子曲线的最大值2.131 MPa·m1/2。
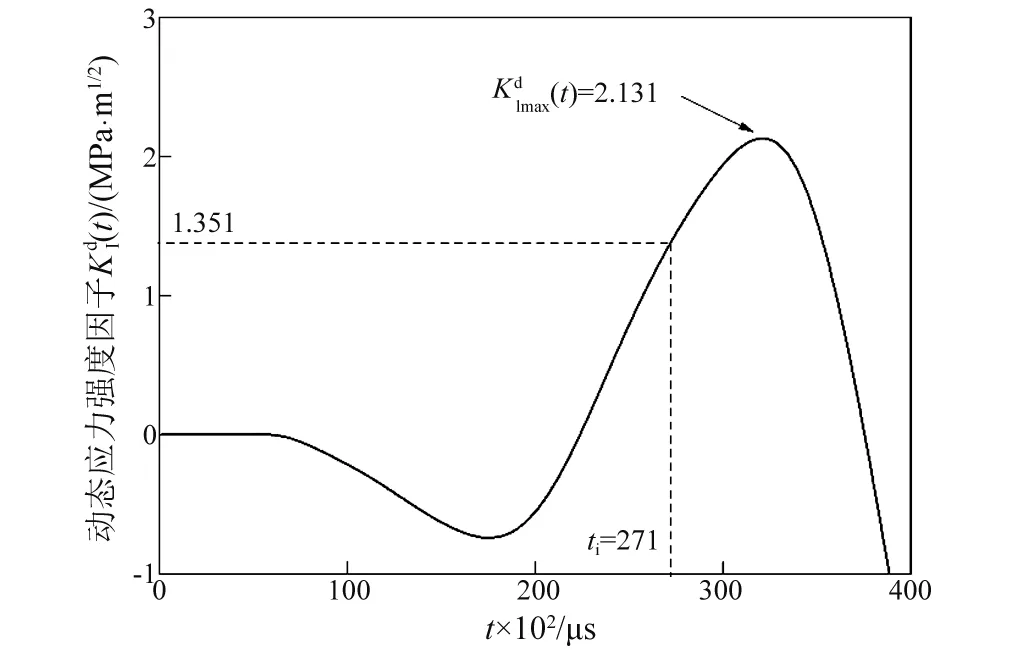
图10 预制裂纹尖端开裂前应力强度因子演化Fig.10 Stress intensity factor of initial cracking at the crack tip
3.3 动态加载率与起裂韧度的关系
在巷道内预制裂纹起裂前,动态试验不会像静态试验形成局部化的集中应变,产生较多的微裂纹,数量相对较少。因此岩石材料在高加载率情况下对断裂的抵抗能力将较高于静态或低加载率情况。根据15组所确定的动态起裂韧度与动态加载率的关系,最后进行分析得到的曲线,如图11所示。从图11可知,动态加载率的增加,裂纹起裂韧度逐渐增大。当动态加载率为257.898 GPa/s时,动态起裂韧度为1.351 MPa·m1/2;当动态加载率为350.189 9 GPa/s时,动态起裂韧度为3.052 MPa·m1/2。在动态加载率为202.163~357.881 GPa/s,动态起裂韧度随着动态加载率的升高,有明显增加的趋势,这与文献[30]采用圆孔内单边裂纹平台巴西圆盘试件得出的结果基本吻合。
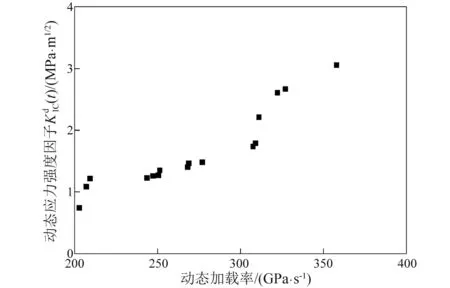
图11 动态加载率与动态起裂韧度Fig.11 Dynamic loading rate and dynamic initiation toughness
4 结 论
本文采用落锤冲击试验机进行冲击加载试验,结合CPG对砂岩巷道模型试件内纯Ⅰ型裂纹的扩展特性进行测定,研究了裂纹扩展速度、起裂时间、动态起裂韧度与动态加载高度及动态加载率的关系,获得了以下主要结论:
(1) 随着动态加载高度的增加,裂纹的扩展速度呈逐渐增加的趋势,随后趋于稳定,裂纹扩展速度最终趋于一个极限值,实测的裂纹扩展速度略小于0.38倍砂岩纵波波速(0.38C0)。
(2) 以入射端加载应力曲线上升沿的斜率定义为动态加载率,随着动态加载率的增加,动态裂纹的起裂时间逐渐降低,下降幅度范围约为50 μs。当动态加载率增加到一定程度时,下降幅度逐渐趋于平缓。
(3) 动态起裂韧度随着动态加载率的升高逐渐增大,说明动态加载率越大,巷道内预制裂纹的动态起裂韧度越大。岩石在高应变率作用下对断裂的抵抗能力将较高于静态或低加载率作用下。
