Ⅰ型裂纹的高强混凝土梁断裂性能试验研究

2020-06-06徐玉萍杨丽娟鲁艳超

科学技术与工程 2020年12期

徐玉萍,杨丽娟,鲁艳超

(1.华东交通大学交通运输学院，南昌 330013；2.华东交通大学经济管理学院，南昌 330013；3.山东省建筑设计研究院青岛分院，青岛 266000)

高强混凝土以其抗压强度高、抗变形能力强、密度大、孔隙率低等优越性，在高层建筑结构、大跨度桥梁结构以及某些特种结构中得到广泛的应用。工程中混凝土一旦开裂就可能会引起钢筋的锈蚀，影响结构的安全与耐久性，因此对混凝土结构在外部荷载下的断裂特性研究，对混凝土结构的抗裂设计及损伤结构的剩余强度具有重要意义。邓宗才[1]通过三点弯曲梁对高强混凝土的断裂韧度以及应力强度因子进行了相应研究，分析了裂纹相对深度变化对断裂韧度的影响并探讨了高强混凝土的断裂机理等问题，研究表明高强混凝土的断裂韧度明显大于普通混凝土的断裂韧度，试件相对裂缝深度对断裂韧度有一定的影响。而Giaccio等[2]采用不同粗骨料研究了高强混凝土的断裂能，结果表明断裂能依赖于骨料的粒径，随着混凝土强度的提高，其断裂能增大。Sener[3]对单轴受压的高强混凝土圆柱体试件进行了尺寸效应的研究，试验结果证明了Bazant尺寸效应率能够·较好的描述高强混凝土抗压强度的尺寸效应，并且大尺寸试件的脆性破坏特征较小尺寸试件更加明显。Tokyay等[4]、Viso等[5]对40～90 MPa高强混凝土的形状效应和尺寸效应进行了试验研究，结果表明立方体试件的尺寸效应较明显，而长细比对高强混凝土试件的抗压强度影响较小。此外，中外学者发现混凝土强度、骨料种类和尺寸、龄期、配合比、试件尺寸等都对混凝土断裂韧度有影响[6-10]。

在双K理论模型的基础上引入双G理论模型作对比[11]，结合试验研究分析高强混凝土在静力荷载作用下的断裂性能以及高强混凝土三点弯曲梁整个断裂过程区的发展过程。分析初始缝高比对裂缝尖端应力强度因子、断裂韧度、断裂过程区长度等的影响。

1 试验材料的制备及试件设计

1.1 试验材料的制备

试验混凝土的强度等级为C60，混凝土材料均采用同一配合比。砂子为河沙，粒径为5 mm；骨料为普通石灰石碎石，最大骨料粒径在20 mm左右，水泥采用江西水泥厂制P.O 42.5普通硅酸盐水泥。配合比设计参照《普通混凝土配合比设计规程》(JG J55—2011)。为了确保试验的准确性，在浇筑之前测试了砂子的含水率，所使用的砂子含水率为4.84%。高强混凝土配合比例如表1所示。

表1 高强混凝土配合比例Table 1 High strength concrete proportion

1.2 试件设计

试验采用标准三点弯曲梁试验方案，如图1所示。试验共浇筑了4组不同尺寸(跨度分别为320、400、480、560 mm)和5种初始缝高比(0.1、0.2、0.3、0.4、0.5)的混凝土试件梁，每种尺寸浇筑3个，共计60个。

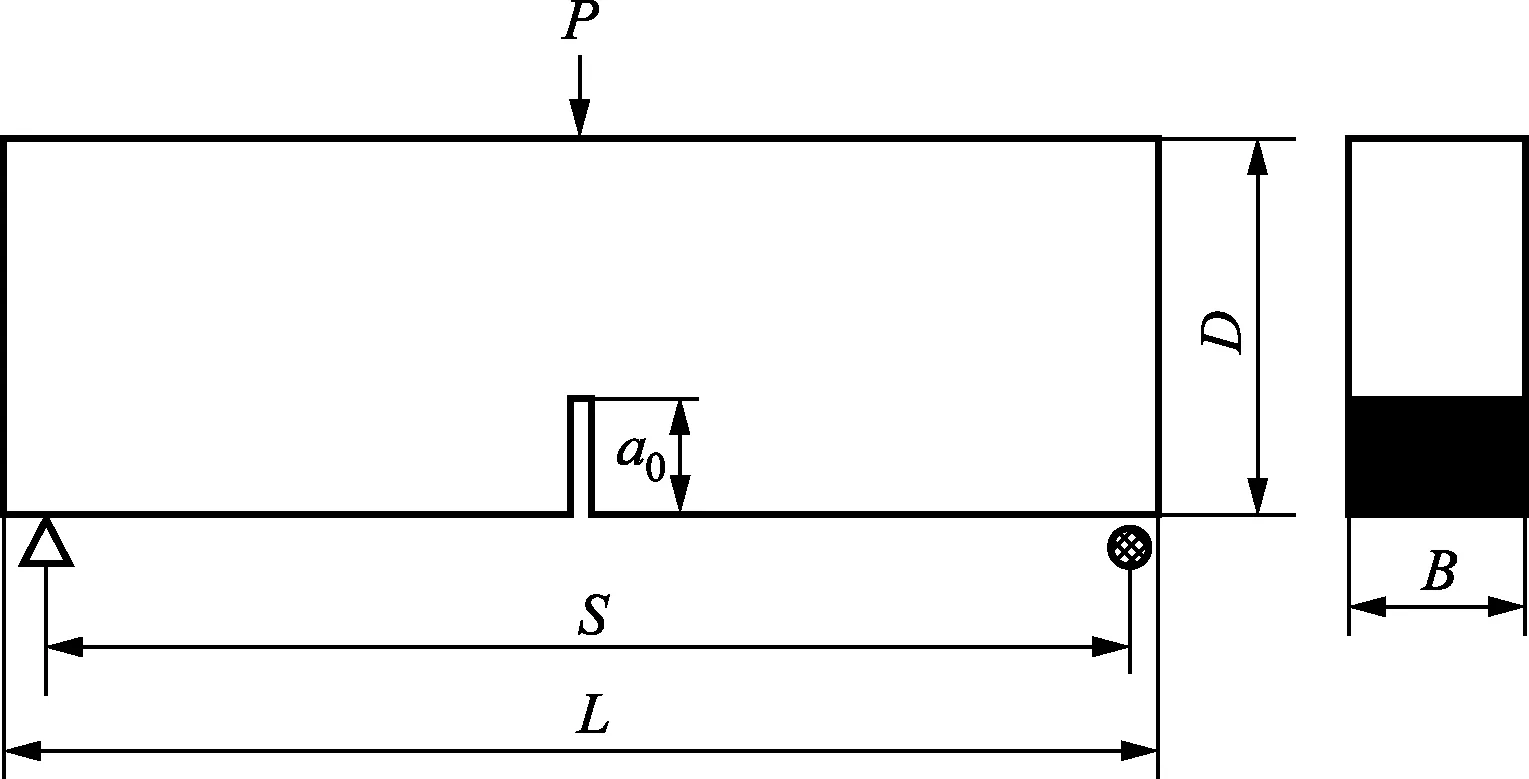
S为试件梁的跨度；L为总长度；a0为初始缝长；B为厚度；D为高度；P为集中荷载图1 三点弯曲梁试验方法Fig.1 Three point bending beam test method

2 荷载值的测定

通过查阅大量文献发现，试验测量起裂荷载的方法有很多，采用较简单、精度高的电阻应变片法[12-14]，这种方法是采用电阻应变片对称粘贴在试件裂缝尖端处来监测应变的变化情况，从而获取起裂与破坏荷载值。表2列举了部分试验试件(TPB-400-10、TPB-400-20、TPB-400-30、TPB-400-40、TPB-400-50)的荷载与应变。

表2 试验荷载与应变值Table 2 Test load and strain value

注：TPB-XX-xx中，TPB为三点弯曲试件梁；XX为梁的长度；xx为初始缝高比；—表示该项无数值。

3 试验结果及断裂特性分析

3.1 初始缝高比对荷载值的影响

分析表3得到的试验数据，分别绘制初始缝高比对(Pmax-Pini)/Pmax的关系曲线(图2)、初始缝高比与Pini/Pmax的关系曲线(图3)、初始缝高比对起裂荷载Pini和最大荷载Pmax的影响(图4)。

由图2可知，(Pmax-Pini)/Pmax基本保持不变，不会随着初始缝高比的变化而变化。数据采用Origin 8.0进行线性回归，得到线性方程为

y=0.305-0.048x

(1)

由回归方程[式(1)]可知其斜率基本为0，y大致在0.3附近波动。

表3 试验断裂性能数据Table 3 Test fracture performance data

图2 (Pmax-Pini)/Pmax与初始缝高比的关系曲线Fig.2 Relation curve of (Pmax-Pini)/Pmax and initial seam height ratio

由图3可知，Pini/Pmax不会随着初始缝高比的变化而变化，同样采用Origin 8.0进行线性回归，得到方程为

y=0.698+0.04x

(2)

由回归方程[式(2)]可以看出，其斜率基本为0，y大致在0.7附近波动。

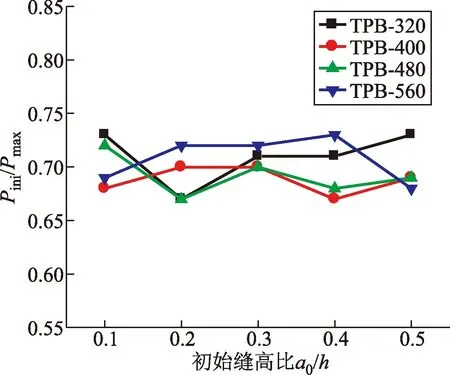
图3 缝高比与Pini/Pmax的关系Fig.3 Relationship between seam height ratio and Pini/Pmax

由图4可知，起裂荷载Pini和最大荷载Pmax均随着初始缝高比的增大而逐渐变小，尤其是初始缝高比从0.1变化到0.2时，荷载值下降幅度相对较大；初始缝高比从0.2变化到0.5时，荷载降低幅度较小，基本保持相同速率降低。另外，最大荷载相比起裂荷载而言，降低幅度相对较大。当跨度S=560时，随着初始缝高比的增大，最大荷载值从10.353 kN降低至3.344 kN；起裂荷载从7.160 kN降低至2.264 kN。当跨度S=320时，随着初始缝高比的增大，最大荷载值从8.082 kN降低至2.486 kN；起裂荷载从5.860 kN降低至1.822 kN。可以看出跨度越大，其降低幅度也相对较大。

图4 初始缝高比对Pini和Pmax的影响Fig.4 Effect of initial seam height ratio on Pini and Pmax

3.2 初始缝高比对起裂韧度的影响

根据文献[15]对于带预制裂纹的三点弯曲梁，断裂韧度可以采用式(3)～式(6)计算(任意α和β≥2.5范围内有效)。

(3)

式(3)中：kβ(α)为对应于β的形状函数，其表达式为

(4)

式(4)中：p4(α)、p∞(α)为关于初始缝高比α的三次多项式：

p4(α)=1.9+0.41α+0.51α2-0.17α3

(5)

p∞(α)=1.99+0.83α-0.31α2+0.14α3

(6)

式中：α=a/D；β=S/D。

将试验值Pini(表3)代入式(5)、式(6)，可以求出起裂韧度，结果如表4所示，然后利用Origin8.0绘制初始缝高比对起裂韧度的影响。

由图5可知，初始缝高比为0.1～0.2时，起裂韧度呈增大的趋势；但初始缝高比为0.2～0.5时，起裂韧度出现了略微下降的趋势。为了更加直观清楚地分析整体的趋势，在只考虑初始裂缝，不考虑跨度的影响下，进行拟合，得到线性回归方程：

y=0.963 8-0.052x

(7)

从式(7)也可以看出初始缝高比与起裂韧度之间的关系，其斜率为负值，起裂韧度子会随着初始缝高比呈现下降的趋势，但回归方程斜率较小，起裂韧度的下降幅值几乎可以认为为0，即起裂韧度一般不会随着初始缝高比的变化而变化，起裂韧度的值大致保持在0.96 MPa·m1/2附近。

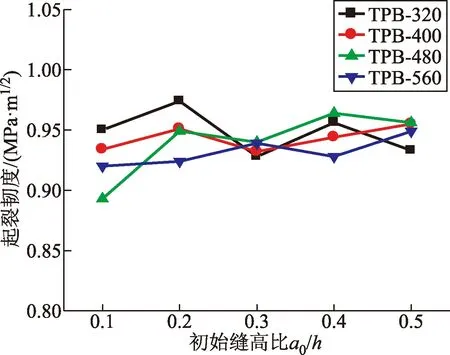
图5 初始缝高比对起裂韧度的影响Fig.5 Influence of initial crack depth ratio and stress intensity factor

3.3 初始缝高比对双K断裂韧度的影响

混凝土的断裂过程大致分为三个阶段：裂纹的起裂、扩展及失稳破坏。如果仅采用传统的理论参数，如临界应力强度因子、能量释放率G、J积分等来分析混凝土的整个断裂过程区，显然是不够充分说明其发展过程的。所以，Xu等[16]、荣华[17]在此基础上，通过大量的试验数据，以应力强度因子为控制参量，提出了混凝土双K断裂模型。

(8)

(9)

(10)

(11)

通过试验测定试件的起裂荷载与失稳荷载，通过双K断裂模型式(8)～式(11)可以得出试件的起裂韧度与失稳韧度，结果如表4所示。

表4 试验数据结果Table 4 Test data results

根据表4数据绘制初始缝高比对双K断裂韧度的影响曲线(图6)。由图6可知，起裂韧度基本不会随着初始缝高比的变化而变化。并且起裂韧度基本保持在0.65 MPa·m1/2，这与荣华[17]的研究结果相同。同样，其值也不会随着跨度与梁高而改变，可以作为材料本身固有断裂性能的材料表征。而对于失稳韧度，从图6中可以看出，当初始缝高比从0.1变化到0.2时，失稳断裂韧度有略微的增大趋势，而随后失稳韧度开始下降，初始缝高比从0.2变化到0.4时，失稳断裂韧度也从1.05 MPa·m1/2下降到了0.95 MPa·m1/2左右。最后，初始缝高比从0.4变化到0.5时，断裂韧度数值又有所上升，但整体的趋势只在微小的范围内浮动，失稳韧度一般分布在1.0 MPa·m1/2左右。同样，失稳韧度和起裂韧度也不会随着跨度与梁高而改变。所以，失稳断裂韧度和起裂断裂韧度可以作为材料本身所固有的断裂性能。

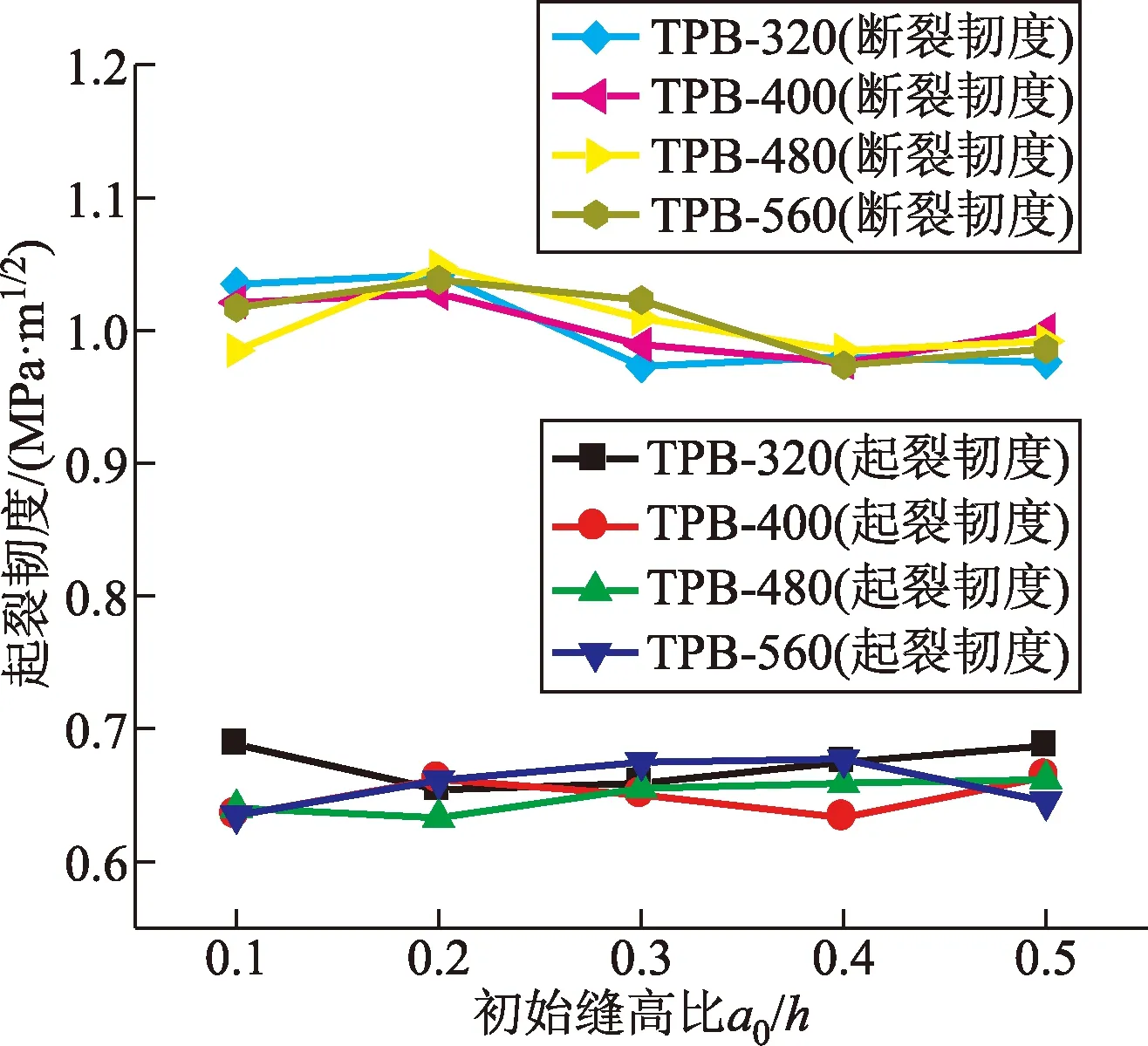
图6 初始缝高比对双K断裂韧度的影响曲线Fig.6 Effect of initial fracture height ratio on fracture toughness of double K

3.4 初始缝高比对双G断裂韧度的影响

混凝土双G断裂模型[18]从本质上和双K断裂模型相同，都是以线弹性理论为基础。故将起裂和失稳视为两个不同线弹性状态，在任意时刻三点弯曲试件梁的能量释放率为

(12)

式(12)中：B为试件的厚度；α=a/D为相对梁高的缝长；C为试件的柔度系数，C=P/δ，其中P为荷载值，δ为荷载挠度曲线的挠度。

根据式(13)可求出dC/dα：

(13)

式(3)中：E为混凝土试件的弹性模量；V(α)为关于缝高比α的四次多项式，V′(α)为V(α)的导数。

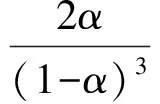
73.64α-104.82α2-51.08α3)

(14)

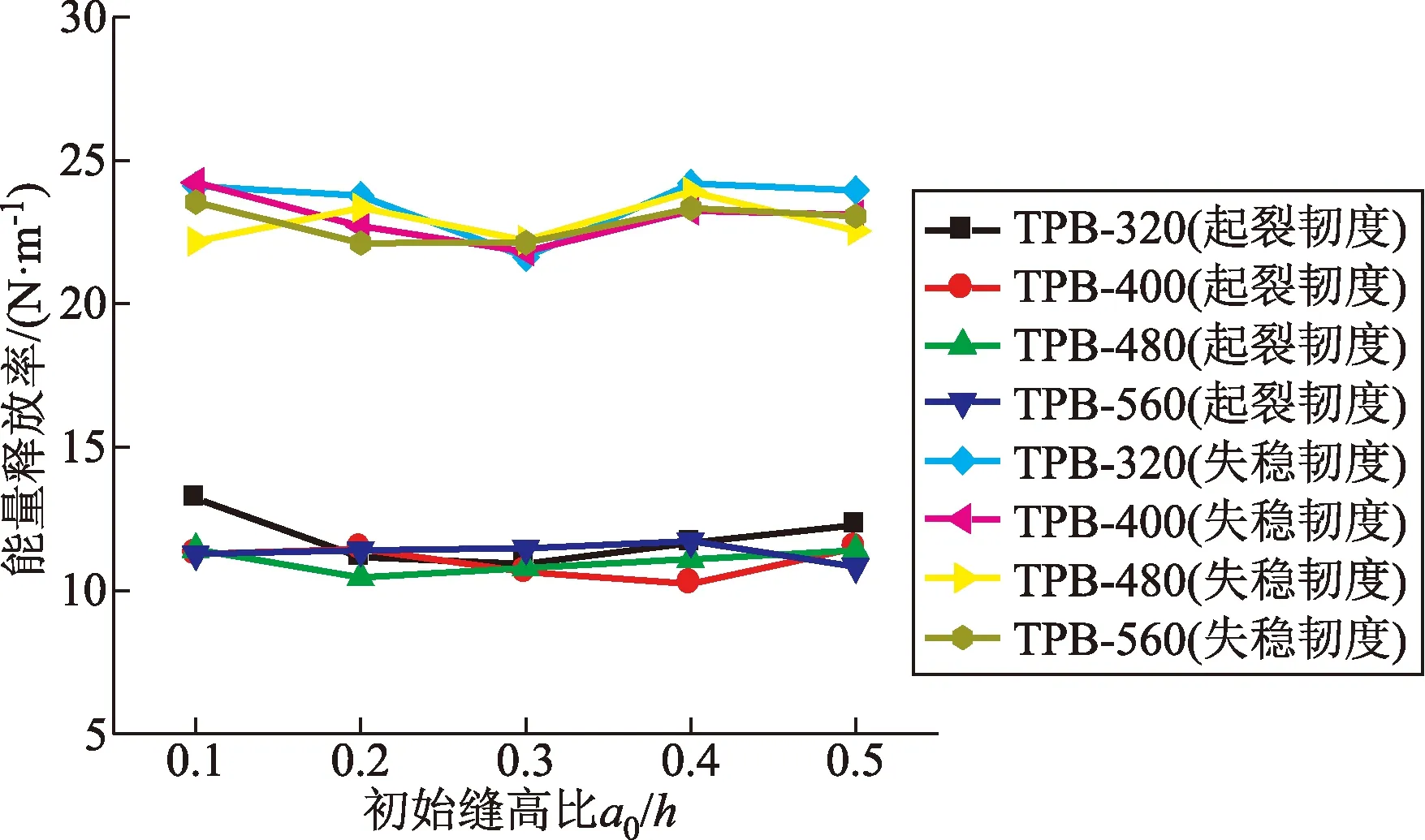
图7 初始缝高比对双G断裂韧度的影响曲线Fig.7 Effect of initial fracture height ratio on fracture toughness of double G

由图7可知，能量释放率G一般不会随着初始缝高比的增加而变化。但也有个别的试件偏离平均值范围附近，如TPB-320-8试件的起裂韧度达到13.5 N/m左右，高于平均值12.5%；失稳韧度降低至21.4 N/m，低于平均值10.83%。但起裂韧度基本上平均值在12 N/m附近，失稳韧度平均值在 24 N/m附近。

3.5 双K断裂模型与双G断裂模型比较分析

双K断裂韧度与双G断裂韧度都是根据修正线弹性断裂力学对混凝土的稳定状态进行判定的，从这一点考虑出发，两者具有相同的效力。根据表2、表3的试验数据对二者的关系进行比较分析。为了客观容易地看出两者之间的关系，将双G断裂韧度按式(14)转换为双K断裂韧度表示为

(15)

式(15)中：G为能量释放率，最后计算结果如表4所示。

起裂韧度与断裂韧度不会随着初始缝高比和梁高的变化而变化。所以取相同初始缝高比试件的平均值，然后通过Origin8.0绘制对比图，如图8所示。

图8 双K与双G断裂参数的比较Fig.8 Comparison of double K and double G fracture parameters

由图8(a)可知，当初始缝高比为0.1时，双K断裂模型与双G断裂模型得出的起裂韧度大致相同，双K断裂模型得出的起裂韧度为0.649 MPa·m1/2，而双G断裂模型得出的起裂韧度为0.651 MPa·m1/2，误差达到最小值，基本相同。当初始缝高比从0.2变化到0.5时起裂韧度则有所增加，初始缝高比等于0.3时起裂韧度达到最大值。双K断裂模型得出的起裂韧度是0.628 MPa·m1/2，而双G断裂模型得出的起裂韧度是0.66 MPa·m1/2，误差达到5.09%。综合所有初始缝高比之间的误差，可以得出双K断裂模型得出的起裂韧度高于双G断裂模型得出的起裂韧度，大致高出3%左右。

由图8(b)可知，初始缝高比从0.1变化到0.3时失稳韧度相对较大，最大时是在初始缝高比等于0.3时，双K断裂模型得出的失稳韧度是1.035 MPa·m1/2，双G断裂模型得出的失稳韧度是0.91 MPa·m1/2，误差达到12.08%。当初始缝高比从0.4变化到0.5时其失稳韧度相对误差较小，双K断裂模型得出的失稳韧度是0.98 MPa·m1/2，双G断裂模型得出的失稳韧度是0.926 MPa·m1/2，误差达到5.94%。综合所有初始缝高比之间的误差，可以得出双K断裂模型得出的起裂韧度高于双G断裂模型得出的起裂韧度。

由图8可知，双K断裂韧度与双G断裂韧度比较接近，且两者变化的趋势大致相同，反映了两者之间的真实性，也得出断裂韧度的稳定性，小尺寸试件不具有尺寸效应的问题，判定断裂韧度可以作为材料本身的断裂性能以及材料的基本参数。