近自由表面海流能发电装置VIVACE流激振动的实验研究
2019-02-22徐万海
徐万海, 罗 浩, 孙 海
(1.天津大学 水利工程仿真与安全国家重点实验室,天津 300072;2.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
近年来,全球环境变化一直是人们关注的热点,以石油和煤炭为代表的化石燃料的大量使用,成为众多环境污染因素中“罪魁祸首”。如何经济高效的开发和利用以海流能为代表的可再生清洁能源,是工业界和学术界亟待解决的技术难题。多种有效的海流能发电技术被提出[1-2], Bernitsas等[3]在此研究领域做出了卓越贡献,他们利用水流经过圆柱(群)所激发的圆柱流激振动,开发了海流能发电装置-VIVACE(Vortex-induced Vibration for Aquatic Clean Energy Converter)。VIVACE装置具有对低流速海流适应性强、对海洋生物友好、制造简单、结构可靠、经济性好等诸多优点,近几年相关研究开展得十分活跃[4-7]。
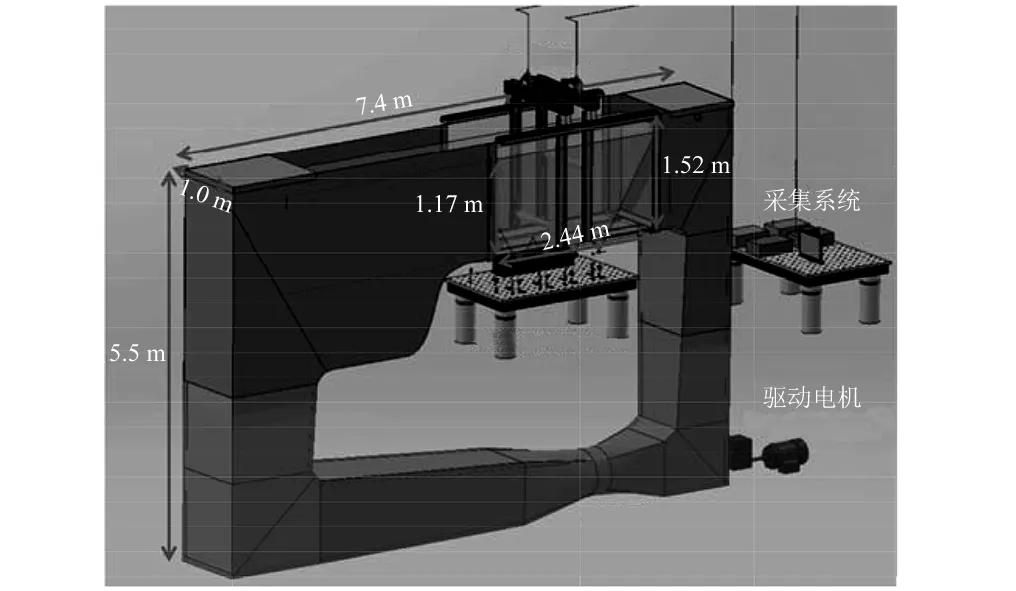
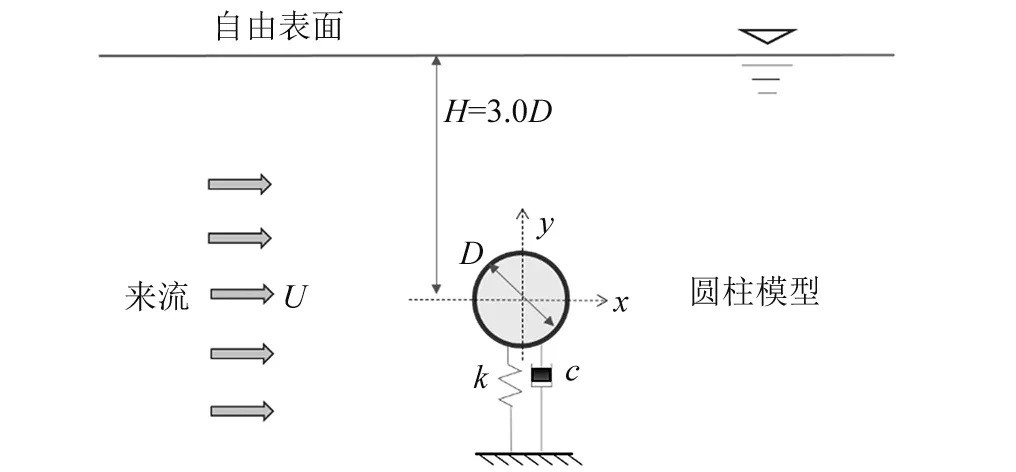
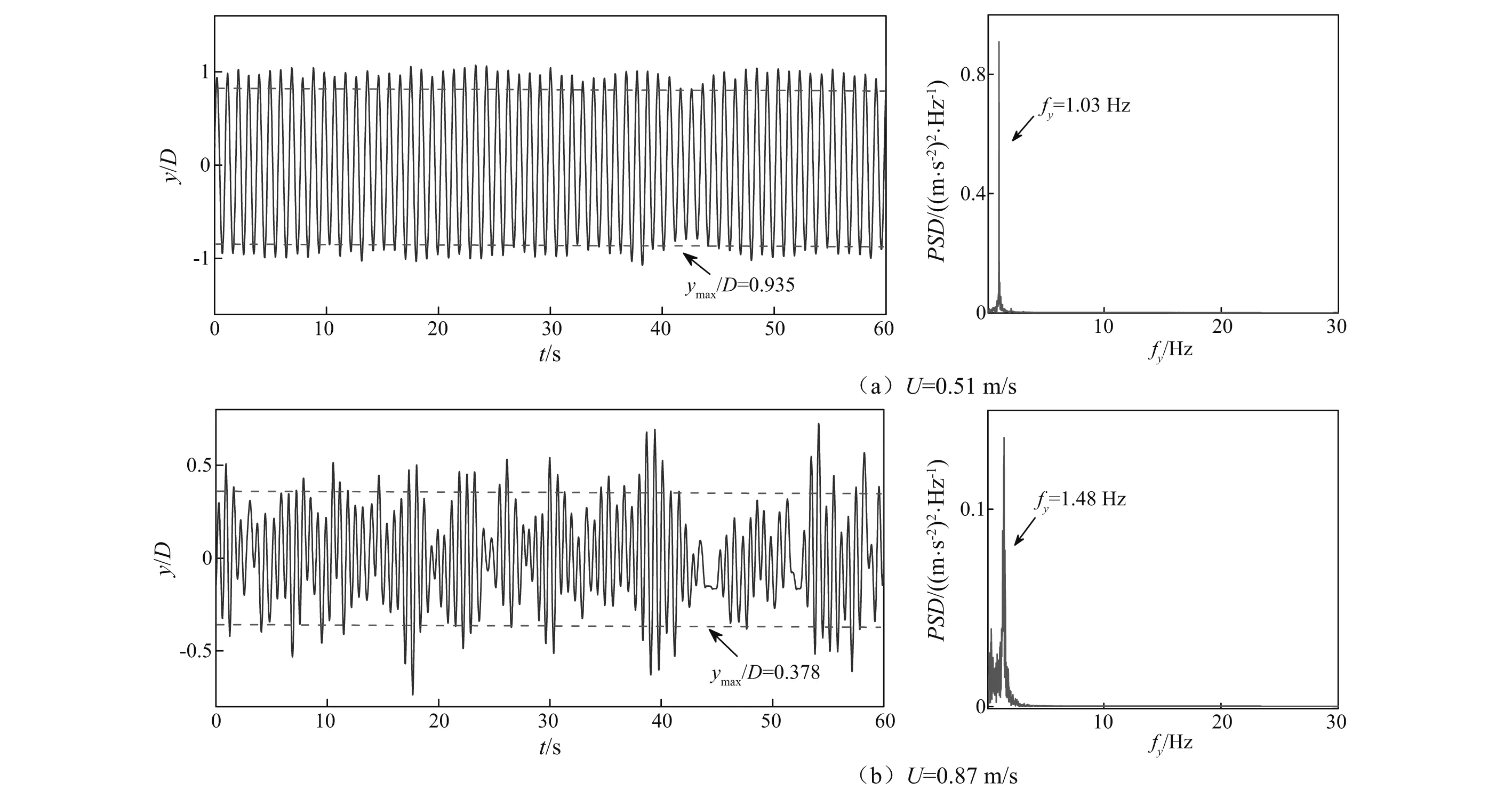
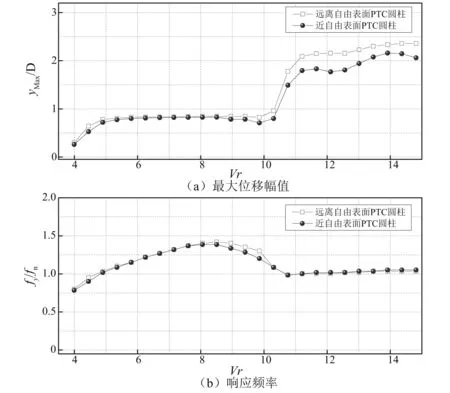
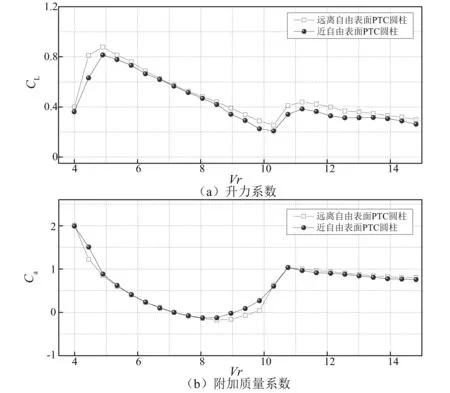
雷诺数(Re)对圆柱流激振动最大响应振幅具有显著作用,Govardhan等[8]给出了最大响应振幅随质量-阻尼参数的变化规律。近期,针对VIVACE流激振动的小质量比(m*=4mosc/πρD2,mosc为圆柱系统结构质量,ρ为流体密度,D为圆柱的外径), 大阻尼比(ζ=ζs+ζharness,ζs为结构阻尼比,ζharness为发电机的阻尼比)和高Re等特点, Raghavan等实验观测了大雷诺数对单个光滑圆柱流激振动的影响规律,发现当2.0×104~4.0×104 VIVACE有时需安装于浅水区或者河流中运行发电,因此自由水面的影响不可忽视。为深入研究自由表面附近光滑圆柱涡激振动特性,需全面探究圆柱尾流区的漩涡脱落模式。Reichl等[9]数值模拟了雷诺数Re=180、弗劳德数Fr(=U/(gD)0.5, 其中U为来流速度,g为重力加速度)介于0~0.7、间隙比H/D=0.1~5.0时(H为圆柱圆心距离自由表面的距离),自由表面附近固定圆柱的绕流流场特性,发现较低Fr时,自由表面变形几乎可忽略; 当Fr>0.3~0.4时,出现了明显的自由表面变化;随着Fr数继续增大,发现了剧烈的自由表面变化现象。Kocabiyik等[10]还关注了近自由表面处,顺流向涡激振动的流体力特征及漩涡脱落规律,并重点分析了自由表面的影响。近期, Chung[11]分析了自由表面附近的弹性支撑刚性圆柱顺流向与横流向涡激振动,发现随着间隙比逐渐变小,规律的漩涡脱落会被一定程度抑制,同时涡激振动响应有减小趋势。整体而言,自由表面效应会减小弹性支撑刚性圆柱涡激振动的共振区间,并降低结构响应幅值。 现阶段,近自由表面的圆柱涡激振动研究大多局限于小雷诺数情形,在大雷诺数条件下,近自由表面处弹性支撑圆柱的涡激振动是否具有较大幅值,亦或振动被抑制,有待进一步探索。同时,人们缺乏对施加了湍流控制的粗糙圆柱,在近自由表面处的流激振动响应规律的认识。上述研究的相对滞后,已大大阻碍VIVACE的设计与工程应用。基于此,本论文开展了相应的实验研究工作,重点观测近自由表面的光滑圆柱与PTC圆柱的流激振动,并与大浸没深度圆柱流激振动实验对比,力图弥补相关流激振动领域的理论不足。 本实验美国密西根大学海洋可再生能源实验室(MRELab)的低湍流循环水槽内开展,通过自动化控制泵的转动,改变来流流速,最大流速为U=1.4 m/s,来流湍流度小于0.098%。水槽整体几何参数为长7.4 m,高5.5 m,宽1.0 m,并设定2.2 m长的观测段,如图1所示。 图1 循环水槽实验系统Fig.1 Schematic diagram of recirculating waterchannel 已有的PTC圆柱流激振动实验表明,在实验水槽允许的来流流速范围内,结构响应幅值可超过2.50D。由于驰振是一种不稳定的振动,随着来流流速的继续增加,响应幅值会进一步加大。因此,实验中设定单圆柱VIVACE系统距离自由表面间隙为3.0D,如图2所示。该间隙的选取可避免测量圆柱跳出水面造成系统损坏,亦可有效地观测自由表面对流激振动的影响。仅允许圆柱在垂直于来流方向发生振动,分别观测了自由表面效应对漩涡脱落激发的光滑圆柱以及PTC圆柱振动特性影响,并对比近自由表面与远自由表面处圆柱振动特性。实验中最大的来流速度1.31 m/s,最高雷诺数为Re=1.18×105。 图2 自由水面附近单圆柱VIVACE示意图Fig.2 Experimental setup for single cylinder-VIVACE near a free surface 当前,弹簧支撑圆柱流致振动实验装置通常采用简单方便的金属弹簧,缺点是一旦确定了硬件系统,弹簧刚度与阻尼调整困难,大大降低了实验效率,甚至影响到实验观测系统的精度。本实验采用虚拟弹簧阻尼系统(Vck)测量结构响应,表1详细列举了Vck系统参数。圆柱直径0.088 9 m,长度0.895 35 m,长度与直径大比值大于10,因此圆柱两端的边界影响可忽略。Vck系统的圆柱质量为7.286 kg,质量比为1.343。Vck系统的弹簧刚度及阻尼比对流激振动的影响规律已得到深入系统的研究,因此,本文仅选取一个弹簧刚度k=500 N/m和发电机的阻尼比ζharness=0.08。 弹性支撑光滑刚性圆柱的涡激振动的锁频区域与约化速度Vr(=U/Dfn)密切相关,随着约化速度增加,依次出现初始分支(Initial branch)、上端分支(Upper branch)和下端分支(Lower branch)[12]。伴随来流的继续增加,弹性支撑光滑刚性圆柱的涡激振动的锁频现象不再出现,这一规律严重限制了VIVACE装置的海流能吸收能力,特别是来流速度比较大的情况下。被动湍流控制技术(PTC)的采用改变了圆柱表面粗糙度,有效调整圆柱表面压力分布,进而引起圆柱升力和阻力的变化。利用了PTC技术,单圆柱VIVACE的振动随约化速度剧烈变化,PTC在VIVACE中的应用,大幅的提高了VIVACE的海流能收集能力。本实验采用PTC60的粗糙带对流动进行控制,详情可参考Sun等的研究。 表1 Vck系统参数 图3 实验数据处理举例,U=0.51 m/s和U=0.87 m/s时光滑圆柱位移时间历程及振动频率Fig.3 Typical example of processing experimental data, time-varying displacement and vibration frequency of the smooth cylinder with U=0.51 m/s and U=0.87 m/s 通过给定单圆柱VIVACE一个较大初始位移,使其自由衰减,根据自由衰减获得的位移时间历程曲线,并做频谱分析,获得了本文实验系统的固有频率为0.998 2 Hz,同时亦可根据式(1)确定VIVACE静水中的固有频率,通过对比理论分析结果与实验结果,可发现本文采用的Vck系统具有较高的精确度。需要指出的是,后续的约化速度Vr计算,结构固有频率fn采用静水中自由衰减实验值。 (1) 将最大位移响应数据的前30%做平均,选取此平均值为最大幅值。振动频率根据快速傅里叶变换(Fast Fourier Transform,FFT)获得。图3给出了两个简单的实验数据处理例子,对应的实验工况为近自由表面的光滑圆柱,来流速度U=0.51 m/s和0.87 m/s,可发现当U=0.51 m/s时,最大无量纲幅值为0.935,振动频率为1.03 Hz;U=0.87 m/s时,最大位移幅值为0.378,振动频率为1.48 Hz。本文的结构振动幅值及频率的确定,均采取此方法。 单圆柱海流能发电装置VIVACE可看作为在垂直于来流方向(即y轴方向)振动的质量-弹簧-阻尼振子,其控制方程如下 (2) 式中:mosc为圆柱系统结构质量;y为横流向的振动位移;k为虚拟弹簧的刚度;Fy为横流向流激振动承受的流体载荷;c为VIVACE整体阻尼; 包括结构阻尼和电机系统阻尼,可表示为 (3) 根据实验观测发现,单圆柱VIVACE的流激振动可简化为正弦形式,因此横流向的振动位移y及流体载荷Fy能够采用如下关系表述 y=y0sin(2πfyt) (4) Fy=F0sin(2πfyt+φ) (5) 根据式(4),可以确定单圆柱VIVACE的振动速度和加速度为 (6) 对式(5)展开分析 Fy=F0sin(2πfyt)cosφ+F0cos(2πfyt)sinφ (7) 圆柱流激振动的横流向流体载荷Fy的真实值可以用升力系数CL和附加质量系数Ca表示为 (8) (9) 通过最小二乘法, 确定升力系数CL和附加质量系数Ca, 具体计算如式(10)和式(11)所示。 (10) (11) 其中, (12) 详细推导过程可参见文献[13]和文献[14]。需要指出,本文第“3”节有关VIVACE流激振动的流体力特性分析时,升力系数CL和附加质量系数Ca均根据结构振动信息,采用式(10)和式(11)间接计算获得。 共开展四个系列模型实验:(a)不考虑自由表面效应的光滑圆柱涡激振动实验;(b)近自由表面对光滑圆柱涡激振动的影响机制实验;(c)不考虑自由表面效应的PTC圆柱流激振动实验;(d)近自由表面PTC圆柱流激振动实验。本部分从三个方面详细阐述实验现象和对应规律:①光滑圆柱流激振动特性;②近自由水面处PTC的控制效果;③PTC圆柱流激振动特性。主要分析单圆柱VIVACE的响应幅值、振动频率、升力系数和附加质量系数特性。 图4绘制了在漩涡脱落激励下,光滑圆柱涡激振动的最大幅值和振动控制频率,为方便结果分析,对位移幅值及振动频率做了无量纲化处理,横坐标为约化速度Vr。可发现,对于光滑圆柱的涡激振动响应,自由表面影响并不明显,主要原因是本文实验自由表面附近布置的圆柱模型间隙距离较远,使得较低流速U条件下,也即为较低约化速度情况时,弗劳德数Fr较小,自由表面效应可忽略。图4中光滑圆柱涡激振动最大位移幅值近似在Vr=6.25时取得,其数值几乎可达1.0D。在整个实验测量速度工况范围内,振动频率fy/fn随约化速度Vr近似线性增加,自由表面对振动频率的影响不明显,再次证明本文实验设定的3.0D间隙距离,不会显著改变弹性支撑刚性圆柱漩涡模式。另一点需指出:当约化速度Vr进一步增大时,自由表面对漩涡脱落频率影响逐步呈现,但由于实验条件限定,我们无法开展更大流速,即对应更大约化速度工况的实验观测,但可推测,来流速度的持续增加,会直接导致弗劳德数Fr不再为小量,位移幅值和振动频率将会受到自由表面效应影响。 图4 近自由表面和不考虑自由表面的光滑圆柱涡激振动最大位移幅值和响应频率Fig.4 Maximum amplitudes and vibration frequencies of surface smooth cylinder and middle smooth cylinder varying with reduced velocity 图5绘制了光滑圆柱涡激振动升力系数CL和附加质量系数Ca随约化速度Vr的变化规律。可发现:当涡激振动的初始分支出现时,近自由表面附近的光滑圆柱升力更小,即自由表面会抑制横流向的升力。但随着来流速度继续增加,上端分支出现,使自由表面的影响逐渐变弱,几乎可忽略。最大升力系数幅值超过了0.8。随着来流速度增加,升力系数CL先逐步增大,后逐渐减小至0, 此时涡激振动的锁频现象几乎消失。附加质量系数Ca几乎一直随Vr增加而减小,最小值接近-0.5。由于附加质量系数Ca的持续减小,才导致图4(b)中振动频率的持续增加。 图5 近自由表面和不考虑自由表面的光滑圆柱涡激振动升力系数和附加质量系数Fig.5 Lift coefficients added mass coefficients of surface smooth cylinder and middle smooth cylinder varying with reduced velocity 图6给出了自由表面附近的光滑圆柱与PTC圆柱最大位移幅值和响应频率随约化速度的变化规律。可发现:PTC圆柱流激振动仍然可以分为三个部分,当4.0≤Vr≤8.0时,PTC圆柱的响应特性与光滑圆柱近似一致,均为涡激振动形式,但其响应幅值略小,振动频率略大。当8.0≤Vr≤10.0时,此时的光滑圆柱涡激振动处于下端分支区域(Lower branch),而PTC圆柱并不存在下端分支,其位移幅值并未出现明显的下降,但是其振动频率却有突然地下降趋势。当约化速度在10.0附近时,PTC圆柱处于由涡激振动向驰振过渡的转化区域,此时相比于光滑圆柱,其位移幅值更大,振动频率更低。当约化速度Vr>10.3时,PTC圆柱位移幅值突然增大,到达驰振区域,并随约化速度线性增加,最大幅值为2.2D。此时光滑圆柱的涡激振动超出了锁频区域,响应幅值很小。当Vr≥14.0时,PTC圆柱驰振位移达到最大值后逐步下降,因为在此约化速度范围内,弗劳德数很大,自由表面的影响凸显。另外可发现,当PTC圆柱驰振发生时,其无量纲的频率值近似为1.0,这表明驰振的频率近似等于PTC圆柱静水中的固有频率。 图6 近自由表面的光滑圆柱与PTC圆柱最大位移幅值和响应频率Fig.6 Maximum amplitudes and vibration frequencies of surface smooth cylinder and surface PTC-cylinder varying with reduced velocity 图7为近自由表面处光滑圆柱与PTC圆柱升力系数和附加质量系数的对比图。可发现:约化速度介于4.0≤Vr≤5.0时,PTC圆柱的升力系数从0.37增加到0.80;当5.0≤Vr≤10.3时,PTC圆柱流激振动的升力系数随约化速度线性减小;当约化速度Vr进一步增加时,PTC圆柱的升力系数CL又开始逐步增加,而后维持在一个相对稳定水平;当约化速度Vr增大到一定量级时,较大的弗劳德数Fr促使升力系数CL出现一定程度下降,此规律也证实了自由表面效应亦会在一定程度上抑制PTC圆柱的流激振动;在较低约化速度对应的涡激振动区域,PTC圆柱与光滑圆柱的升力系数CL具有相似的变化规律,仅取得最大升力系数幅值对应的约化速度存在差异。相比于光滑圆柱,PTC圆柱的附加质量系数Ca随约化速度的变化要更加复杂,当4.0≤Vr≤8.0时,附加质量系数Ca逐步减小;当PTC圆柱振动位于涡激振动向驰振转化区时,附加质量系数Ca会有出现明显增加,直接导致结构振动的频率出现较大幅度的下降,如图7(b)所示。当PTC圆柱的驰振稳定发生时,附加质量系数Ca整体稳定在1.0附近,并随约化速度有细微降低的趋势,这也是为什么图7(b)中驰振的振动频率近似于结构静水中的固有频率的原因。 图7 近自由表面的光滑圆柱与PTC圆柱升力系数和附加质量系数Fig.7 Lift coefficients added mass coefficients of surface smooth cylinder and surface PTC-cylinder varying with reduced velocity 这里进一步分析近自由表面处的PTC圆柱与不考虑自由表面的PTC圆柱流激振动差异, PTC圆柱流激振动最大位移幅值和响应频率的对比图,如图8所示。可发现,在本文观测的实验工况条件下,当振动处于涡激振动范围,自由表面效应对PTC圆柱位移幅值和振动频率的影响很小;随约化速度增加,振动逐步处于涡激振动向驰振转化的区域,此时考虑自由表面影响和不考虑自由表面影响的PTC圆柱响应幅值的差异逐步明显,并在振动处于驰振状态时,位移幅值差异有加大趋势,表明自由表面效应越来越重要,在VIVACE实际设计过程中,这一特性需要重点关注。然而,自由表面效应对振动频率的影响却很微弱,详见图8(b)。 图8 近自由表面和不考虑自由表面的PTC圆柱流激振动最大位移幅值和响应频率Fig.8 Maximum amplitudes and vibration frequencies of surface PTC-cylinder and middle PTC-cylinder varying with reduced velocity PTC圆柱流激振动升力系数和附加质量系数随约化速度变化趋势,如图9所示。通过对比近自由表面的实验工况与远离自由表面的工况,分析自由表面效应对升力系数CL和附加质量系数Ca的作用。可发现:在涡激振动发生区域,自由表面对PTC圆柱的升力系数CL影响较小。当振动处于涡激振动向驰振转化区、以及驰振完全发生区域,自由表面效应强烈制约PTC圆柱的流激振动升力系数CL。出现如此规律的原因,主要是大弗劳德数Fr引起。与升力系数CL不同,自由表面对PTC圆柱流激振动的附加质量系数Ca几乎无影响,详情可参见图9(b)。这一现象说明了自由表面对PTC圆柱流激振动的振动频率影响亦很小,相关规律已在图8(b)中观察得到。 图9 近自由表面和不考虑自由表面的光滑圆柱流激振动升力系数和附加质量系数Fig.9 Lift coefficients added mass coefficients of surface PTC-cylinder and middle PTC-cylinder varying with reduced velocity 本文在低湍流度循环水槽内开展单圆柱VIVACE的流激振动实验,通过虚拟阻尼弹簧系统测量圆柱的振动特性,并确定了流激振动的升力系数和附加质量系数,得到如下结论: (1) 根据本文实验设定的3.0D间隙距离,分析自由表面对光滑圆柱涡激振动的影响发现,自由表面不会显著改变弹性支撑刚性圆柱漩涡模式、位移幅值、升力系数和附加质量系数。获得的最大位移幅值为1.0D,振动频率与约化速度呈现线性增加的关系。同时发现大约化速度条件时,由于对应较大弗劳德数,自由表面影响逐步显著。 (2) 近自由水面PTC圆柱的流激振动根据约化速度由低到高,依次分为三个区域,涡激振动区、涡激振动向驰振转化区和驰振区。在涡激振动区,PTC圆柱与光滑圆柱具有相似的振动特性及流体力系数,在驰振区域,采用了PTC圆柱结构具有很大响应幅值,并且其振动频率与静水中固有频率近似相同,升力系数不再接近于0,而是处于一个相对稳定的数值,附加质量系数近似为1.0。 (3) 当振动处于涡激振动范围,PTC圆柱位移幅值和振动频率受自由表面效应影响小;振动处于驰振状态时,考虑自由表面影响及不考虑自由表面影响的实验结果表明,位移幅值和升力系数差异逐渐增大,表明自由表面效应越来越重要。1 实验设计

2 流体力计算方法
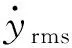
3 实验结果分析
3.1 光滑圆柱涡激振动特性
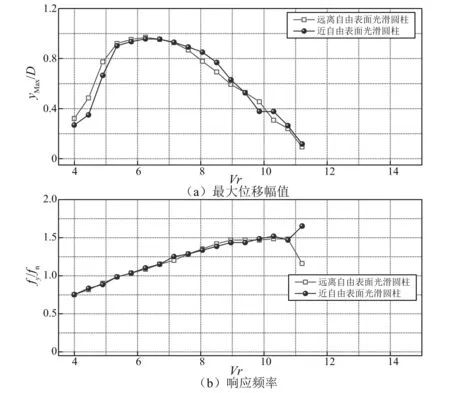
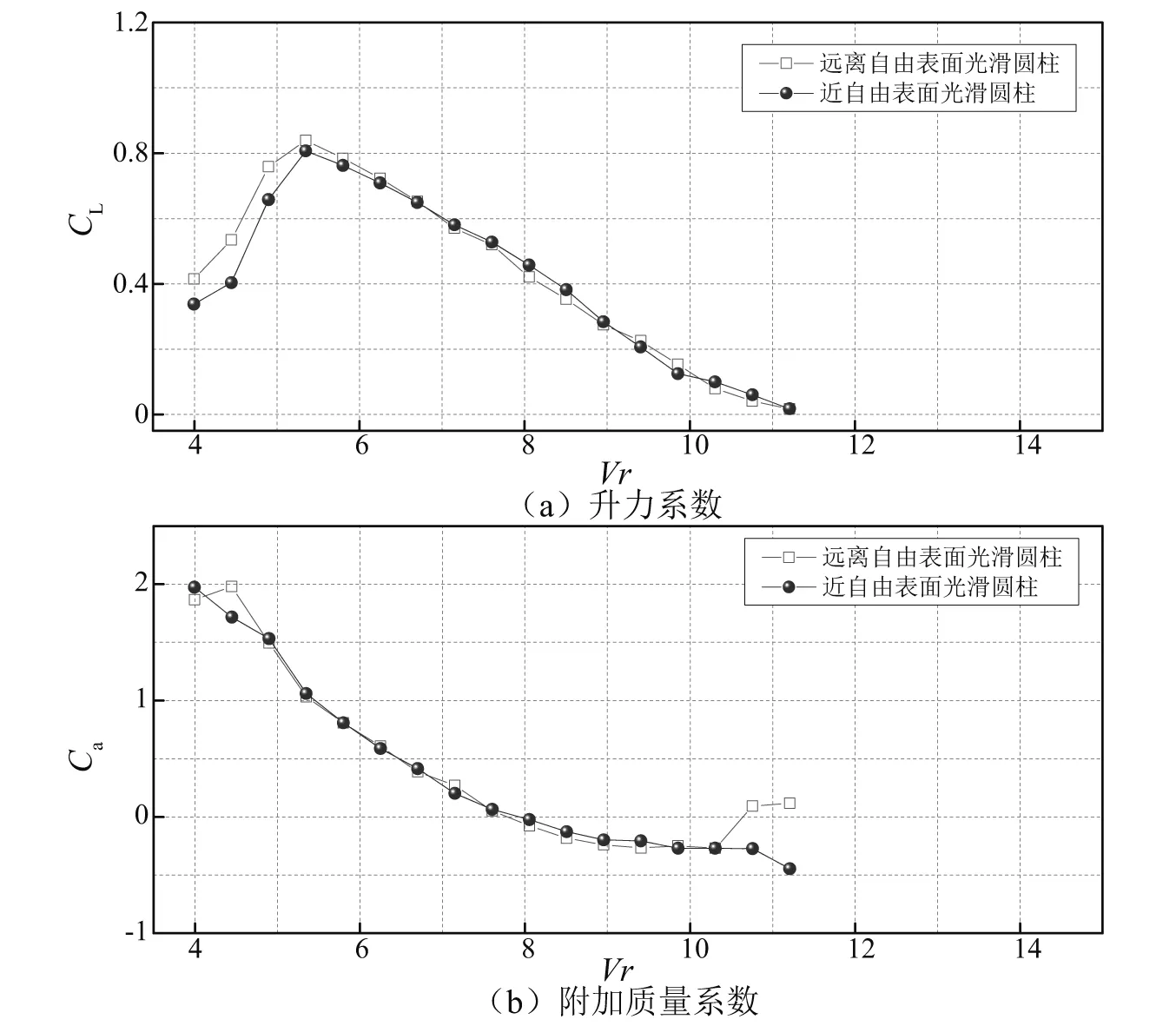
3.2 近自由表面处PTC的控制效果
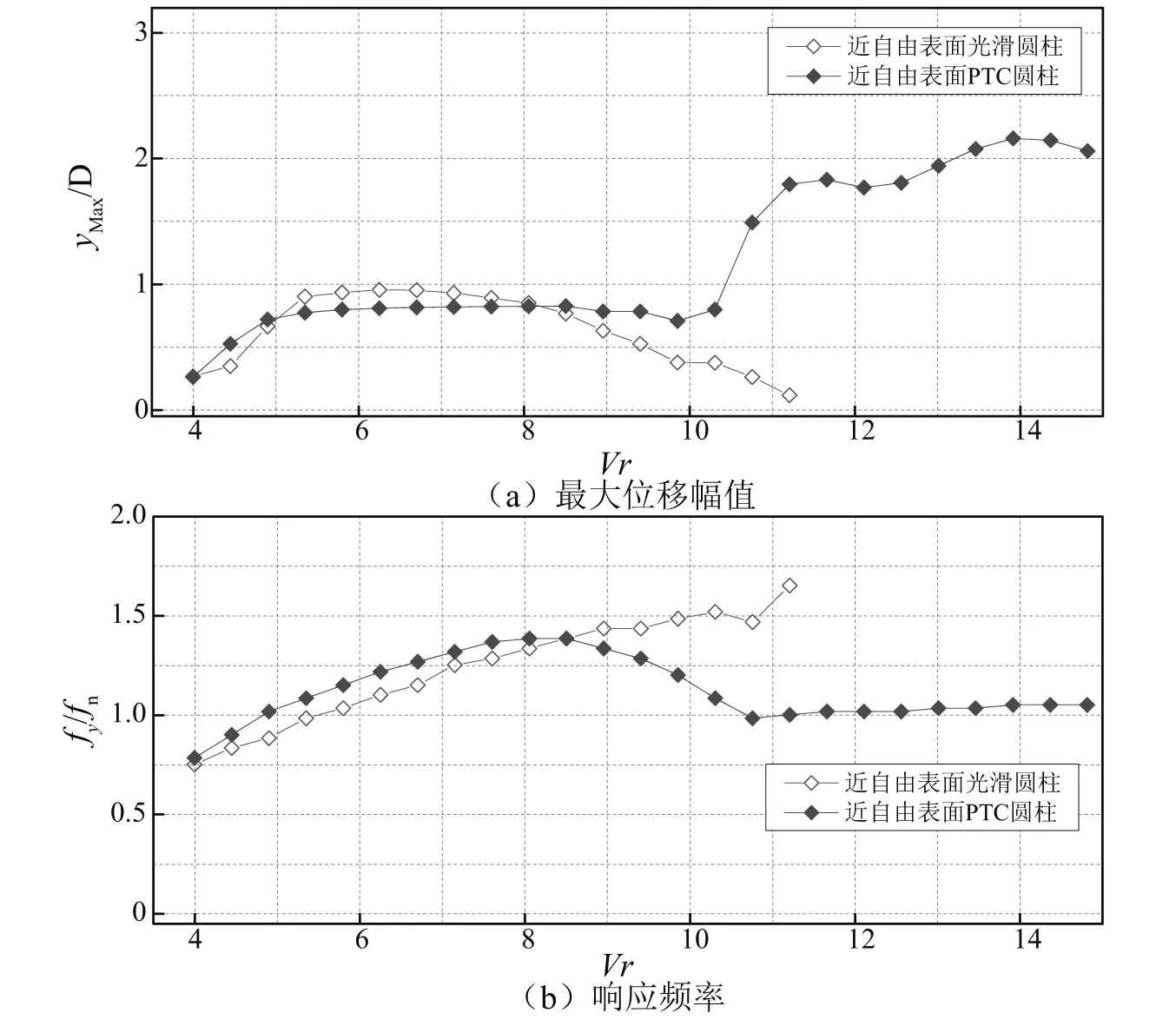
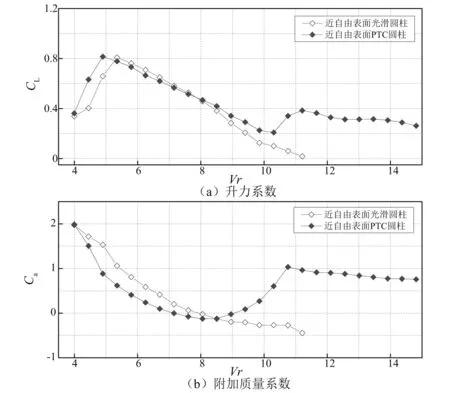
3.3 PTC圆柱流激振动特性
4 结 论
