基于优化函数的PID参数整定技术在液压振动台上的应用

谢海波， 杜泽锋， 卢俊廷， 张泰龙， 杨华勇

(浙江大学机械工程学院， 浙江杭州 310027)

引言

液压伺服系统具有输出力大、响应频率高、控制精度高等优点，在工程中被广泛应用。通常，液压伺服系统简单有效的控制策略为PID控制。在计算机进入控制领域之前，PID控制主要是通过电路硬件的方式实现，其调试过程花费时间较长，效率较低。在计算机进入控制领域之后，PID控制逐渐采用数字计算机组成的计算机控制系统来进行控制。通过软件程序的编写，PID控制更加灵活。目前，数字PID控制是生产过程中最普遍采用的控制方法，在多行业工程中获得了广泛的应用。

然而PID控制的参数调定，一直以来都是困扰科研人员的一大难题。目前研究领域调定PID参数主要的两种方法，一种是借助工程经验进行试凑，另一种是借助计算机软件进行仿真。计算机仿真法因数学模型不够准确，调定的PID参数可靠性较低；经验试凑法调定的PID参数效果较好，但参数调定效率较低，且精度不高。因此本研究提出了一种精确系统辨识并基于最优求解函数的PID快速整定方法。该方法在搭建的伺服实验台上取得了较好的效果，对工程控制有普遍借鉴意义。

1 高频液压伺服振动台

实验台搭建的液压伺服控制系统主要构成有力反馈两级电液伺服阀和双出杆伺服油缸。

1.1 力反馈两级电液伺服阀

力反馈两级伺服阀如图1所示，这种伺服阀由于衔铁和挡板均在中位附近工作，所以线性好。对力矩马达的线性度要求也不高，可以允许滑阀有较大的工作行程。

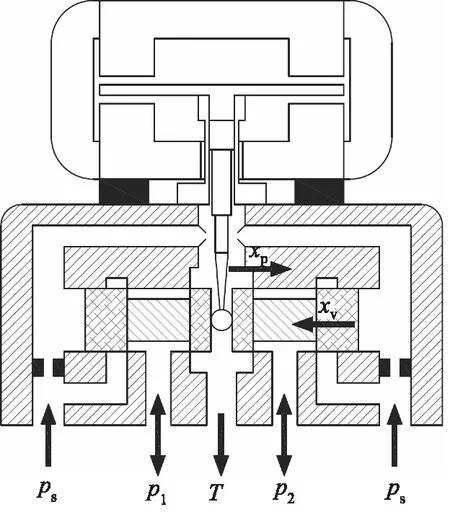
图1 力反馈两级伺服阀结构图

这种伺服阀的简化方框图如图2所示，进而可以推出伺服阀的传递函数为:

(1)

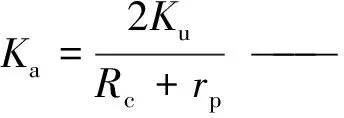
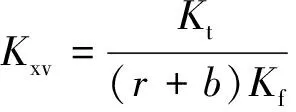
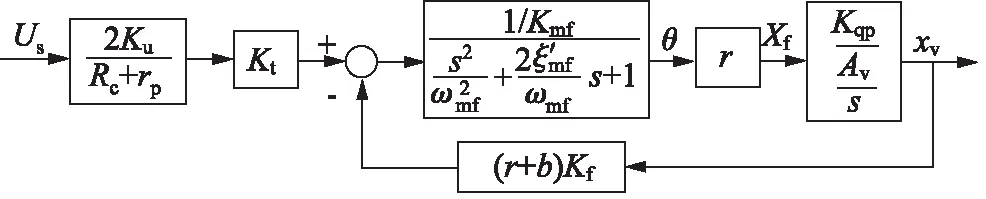
图2 力反馈伺服阀的简化方块图

在伺服系统中，通常以电流作为输入参数，伺服阀的动态响应往往高于动力元件的动态响应，通常还可以进一步简化为二阶振荡环节，即:

(2)

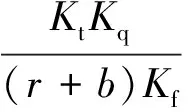
ωsv—— 伺服阀固有频率

ξsv—— 伺服阀阻尼比

1.2 系统数学模型简化

该液压系统参与数学建模的主要部分为：力反馈两级电液伺服阀和带位移反馈的伺服油缸。

伺服阀控制液压缸的环节，在考虑负载质量mt、忽略油液体积变化(即认为油液有效体积模量为无穷大)、负载无阻尼和弹性作用时，阀控缸环节的传递函数可以简化为式(3)的二阶环节。

(3)

式中,ω1为惯性环节的转折频率。

根据伺服阀和阀控缸的简化模型得到系统的方块图如图3所示。

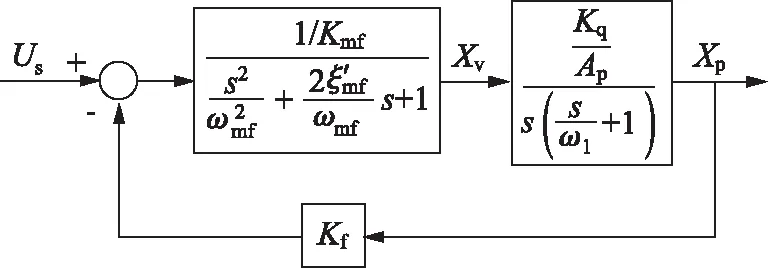
图3 简化后的系统方块图

由方块图的化简可以得出系统闭环传递函数阶次。推知系统的闭环传递函数为4阶0次(即4个极点，无0点)。

1.3 基于MATLAB的系统辨识

伺服阀的结构较为复杂，不便于拆卸与试验，因此伺服阀的关键参数不便于获取。但实验台搭建完成后，伺服缸的位移数据比较容易采集。因此给系统输入特定波形，采集伺服缸的位移数据，然后借助MATLAB的系统辨识工具箱，识别出系统的各阶次系数，得到系统的传递函数，基于MATLAB的系统辨识的流程如图4所示。

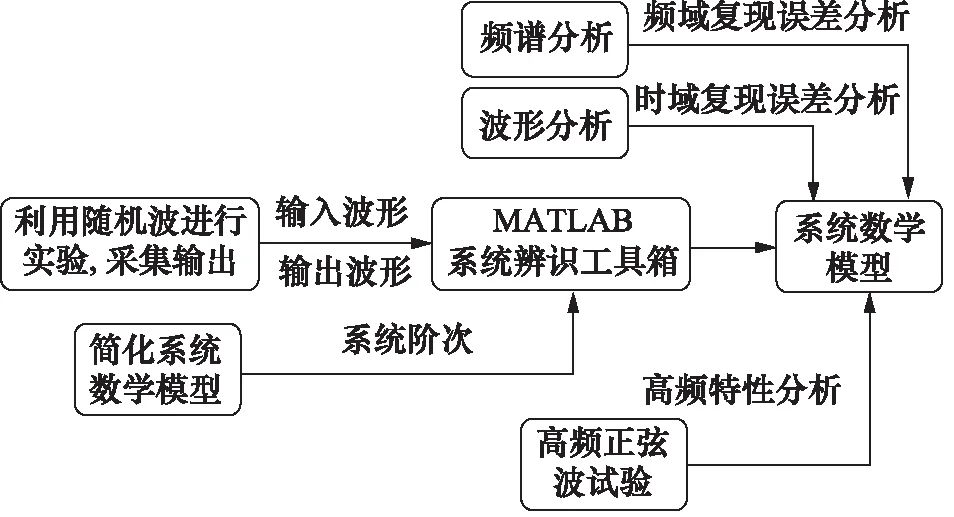
图4 系统辨识流程图

首先对系统输入1组地震波形数据，该波形的主频范围在0～200 Hz。采集油缸的位移反馈信号，采集到的波形如图5所示。

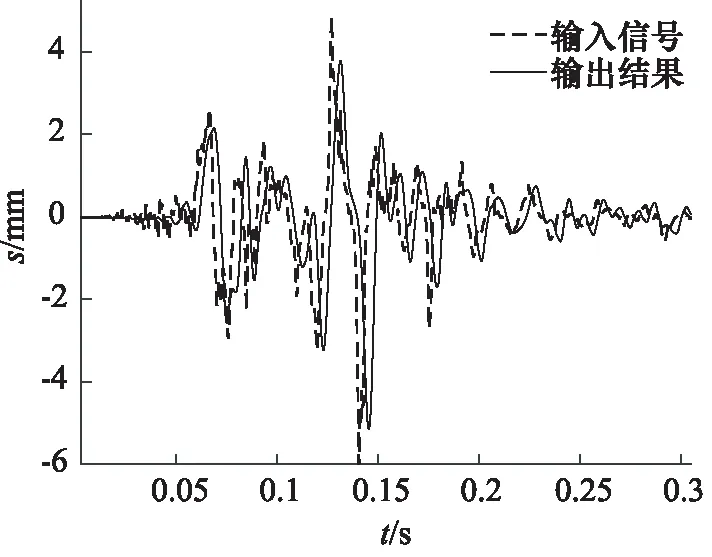
图5 28 MPa随机波形输入输出结果

已经推知系统的传递函数可以简化为4阶0次。将输入给实验台的样本波形数据与采集到的油缸位移数据输入到MATLAB的系统辨识工具箱中。设定待拟合的系统阶次为4阶0次，经MATLAB计算，可以识别出的系统的传递函数为式(4)：

(4)

(注：式中传递函数中，en代表10n)

对得到的实验数据进行Simulink模型搭建，因为实际系统在低频时的跟随特性较好，因此闭环传递函数中的零阶系数可以近似等于3.117×1011，因此可以搭建出Simulink模型如图6所示，其中数值限制模块是为了模拟电压输出板卡的输出电压范围为0～±10 V。

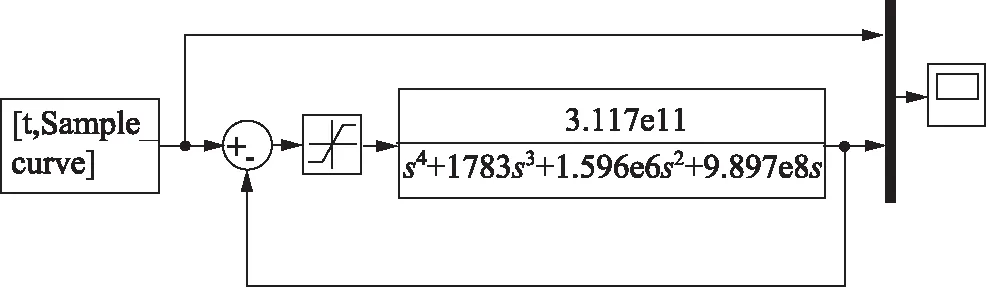
图6 系统的Simulink模型

对模型进行仿真，比较仿真系统的输出波形与输入波形，比较结果如图7所示。同时，将仿真模型输出波形与试验得到的实际油缸位移波形进行对比，对比结果如图8所示，数据显示2个波形的拟合度高达81.5%。虽然可以看出仿真波形和实验输出波形基本重合，但仿真模型在稳态特性和瞬态特性上的可靠性还需要对比进一步验证。

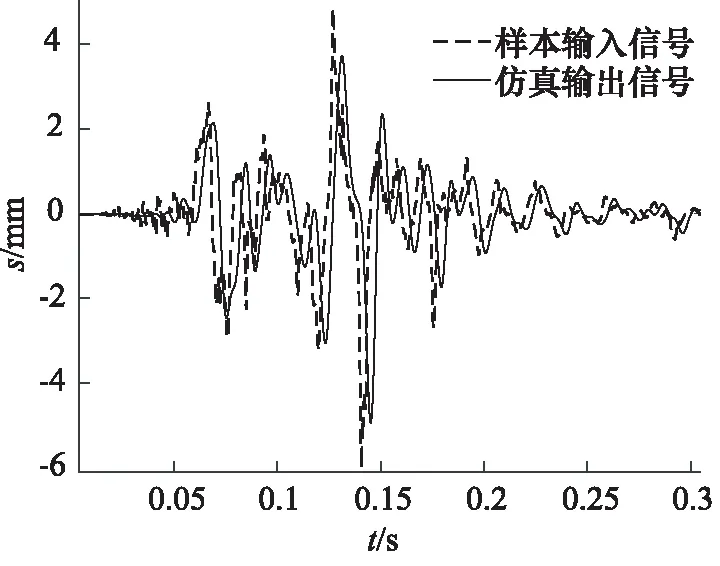
图7 Simulink仿真输出结果

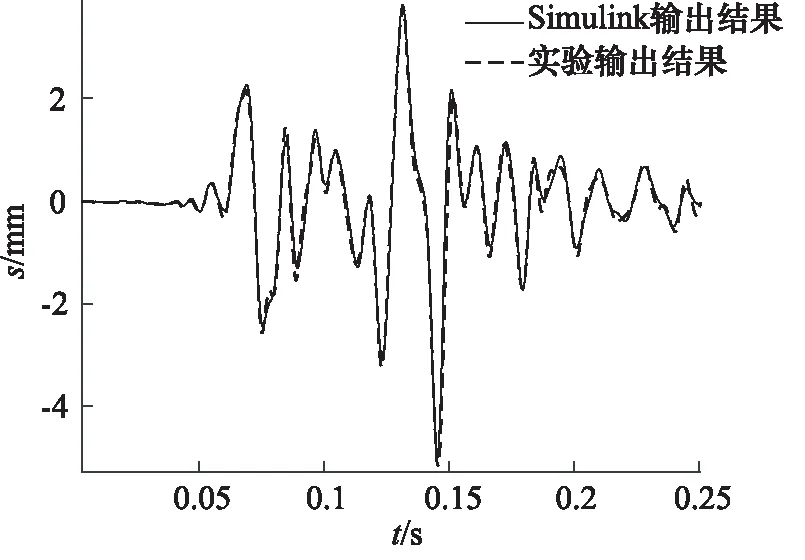
图8 仿真结果与实验结果对比图

利用正弦波进行实验，通过比较仿真输出波形与理论波形在时间和相位上的滞后量以及幅值上的差值，验证系统模型的高频可靠性。构建的正弦波仿真模型如图9所示。因振动台的性能主要体现在高频响应，因此选择频率较高的90 Hz正弦波作为测试波形。

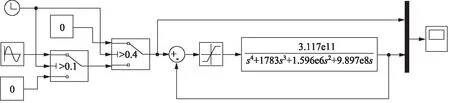
图9 Simulink正弦仿真模型

通过仿真模型仿真得到的结果如图10所示。在实验台上进行测试，输入同样频率及幅值的正弦信号，得到的结果如图11所示。对比实验测得的结果与仿真结果，从关键参数看出，波形的滞后均为0.004 s，即相位滞后129.6°。仿真波形振幅的超调量为2.17%，而实验的振幅波形超调量2.16%。通过该组波形的对比得知，MATLAB的系统辨识的模型与原系统的相似度较高，可以作为仿真模型进行实验。

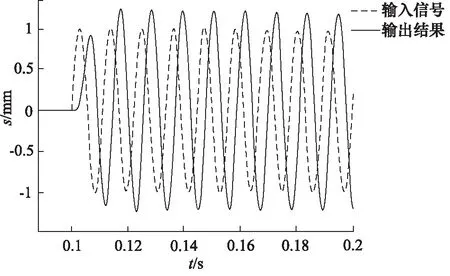
图10 Simulink正弦波仿真结果

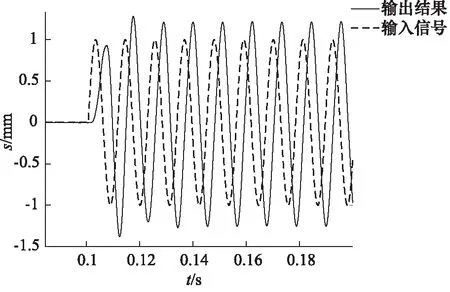
图11 实验台90 Hz正弦波实验结果

2 常见PID控制策略

PID控制算法被广泛应用于各大工程项目之中，能适用于大部分的线性及非线性项目。目前PID控制算法已经比较成熟。针对的液压伺服振动台，选择了以下3种合适的PID控制策略进行分析。

2.1 基本PID控制算法

基本PID控制主要由比例环节、积分环节及微分环节组成。比例环节用以减小误差，积分环节用以消除误差，微分环节主要在加快系统的动作速度，以提高系统的动态性能。

仿真模型中的PID控制器的传递函数为式(5)。在Simulink中建立的基本PID的仿真模型如图12所示。

(5)

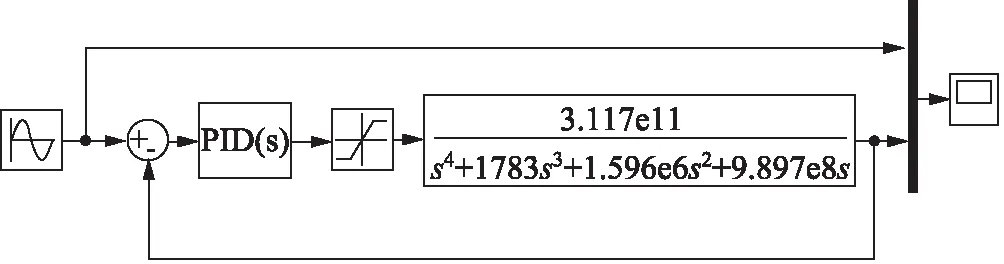
图12 基本PID控制Simulink仿真图

2.2 分离式PID控制算法

在振动台控制系统中加入PID控制策略的主要为了提高系统的快速性，系统的快速性和稳定性是相对矛盾的两个因素。增加了PID控制环节后，系统快速性得到提升的同时，超调量也会相对增大。因此，希望在误差信号较大时和误差信号较小时用两组PID控制器进行分别控制。在误差较大时，主要以增加系统快速性为主，在误差信号较小时，主要以减小系统超调量为主。两组PID控制器的调用，以误差信号的大小作为触发信号。在Simulink中建立的仿真模型如图13所示。

2.3 微分先行PID控制算法

图14为微分先行PID控制算法的原理方块图。

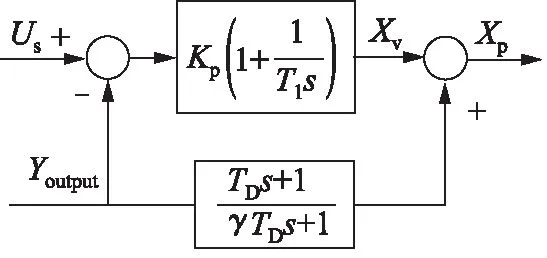
图14 微分先行PID控制原理方块图

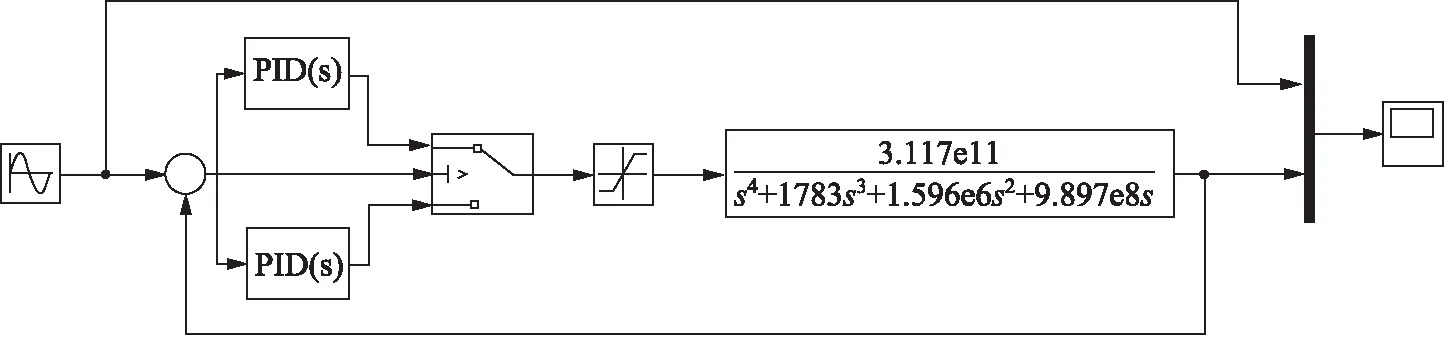
图13 分离式PID Simulink控制模型

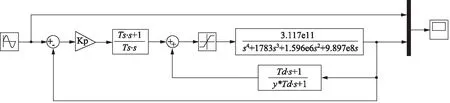
图15 微分先行PID控制Simulink仿真图

的特点是只对输出量进行微分而对输入量不进行微分。因为在输入地震波时，输入量通常是变化比较频繁的，而输出量变化比较缓和。这样的PID控制策略可以避免因为给定量剧烈变化而带来的系统震荡。

在Simulink中搭建该PID控制算法的仿真图，如图15所示。

3 优化函数的运用

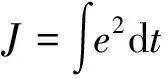
在MATLAB中的最小平方函数为lsqnonlin，设定需要整定的参数，便可以在指定范围内寻找最优解。优化函数的求解步骤如图16所示。

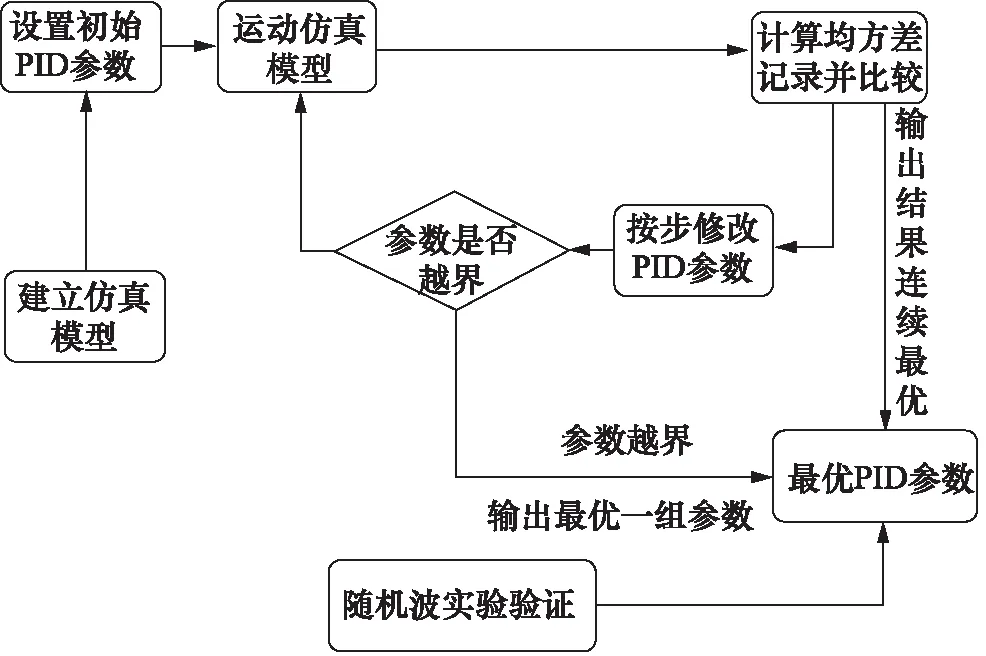
图16 优化函数求解步骤流程图

3.1 基本PID控制仿真求解

利用MATLAB与Simulink联合仿真，均设定PID初始值为[Kp,Ki，Kd，N]=[1 0 0 100]，求解范围为：下限矩阵=[0 0 0 0],上限矩阵=[100 100 100 10000]，求解步长=[1e-3 1e-5 1e-5 1e-2];

用10 Hz的正弦波进行误差求解，求得的PID的最优矩阵为:

[Kp，Ki，Kd，N]=[0.9007 2.1365 1.838e-4 3413.3]

利用求解得到的参数，进行地震波曲线输出，图17为基本PID仿真输出结果。

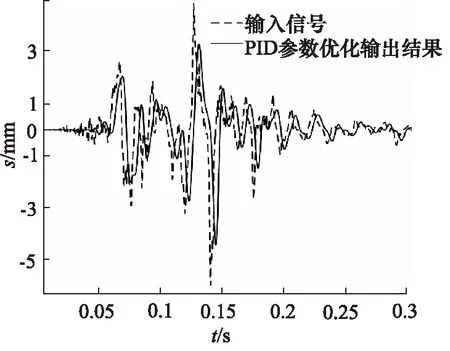
图17 基础PID参数优化仿真输出结果

对仿真结果与原实验结果进行频谱分析，结果如图18所示，可以看出，无PID控制的闭环系统对于80 Hz以上的频率响应会出现明显的超调，表现为80～135 Hz，振幅超调，130 Hz以后迅速衰减。而加入经过参数最优化处理的基本PID控制后，系统在80～135 Hz处的超调现象得到了较好的抑制，曲线在0～135 Hz对原波形的复现效果较好。

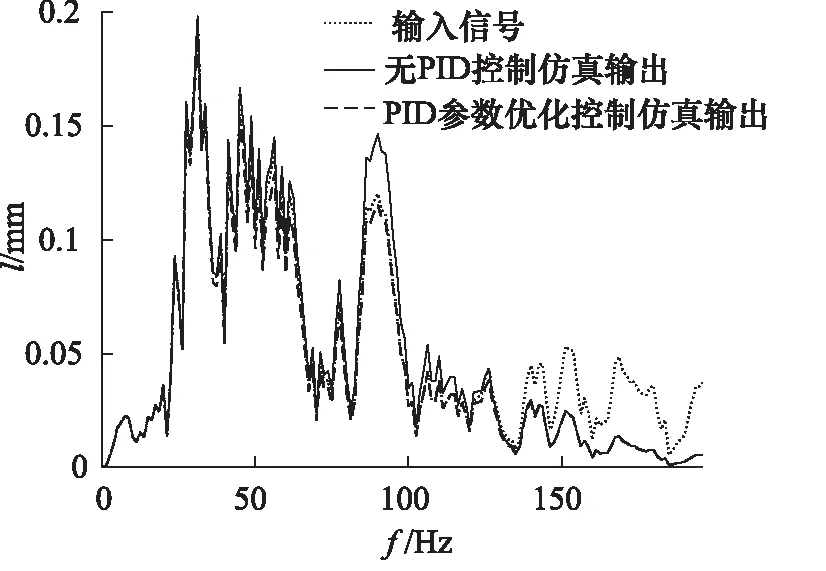
图18 基础PID仿真频谱对比分析

观察得知，加入PID控制的闭环系统与未加PID控制的闭环系统，对90 Hz左右的波形有较为明显的改善。在仿真系统中输入90 Hz的正弦波，输出的结果如图19所示。从90 Hz的正弦波仿真结果可以看出，加入了最优参数PID后的曲线能够较好地跟踪上样本的输入，而无PID校正的闭环系统对该输入波形跟踪情况较差。

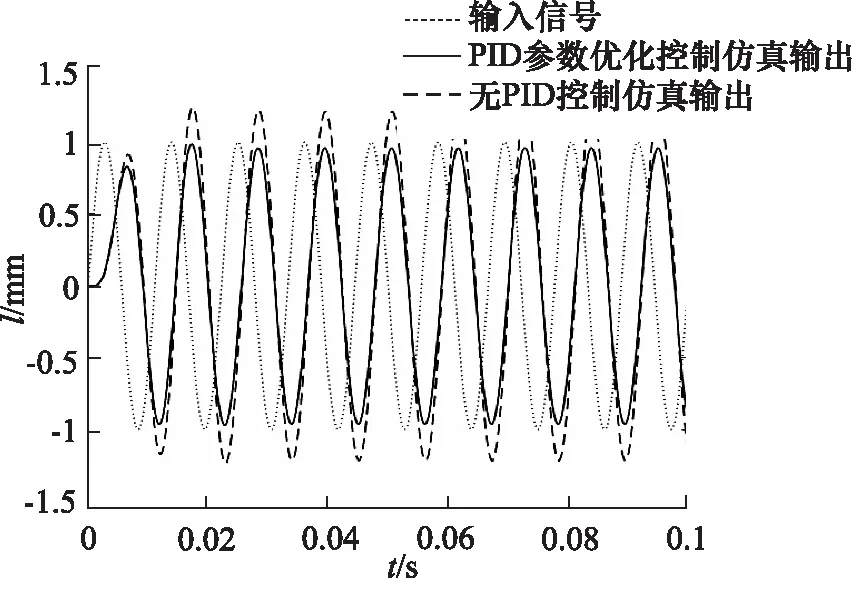
图19 90 Hz正弦波仿真结果

3.2 特殊PID控制方式的最优求解

设定参数，可以对其余PID控制方式进行最优化求解。

对于分离式PID的求解，设定的参数为两个PID控制器的8个参数[Kp1,Ki1,Kd1, N1,Kp2,Ki2,Kd2,N2]以及误差分界点参数e。设定e的求解范围为[0 1]，求解步长为0.0001。最终求解的结果为[Kp1,Ki1,Kd1,N1，Kp2，Ki2，Kd2，N2，e]=[0.2928 8.0853e-30 0.0071 111.2958 0.8073 9.9678e-5 0.0011 33.1529 0.1994]。

用90 Hz的正弦波进行验证，结果如图20所示，发现跟踪效果并无明显改善且输出曲线出现偏置现象。

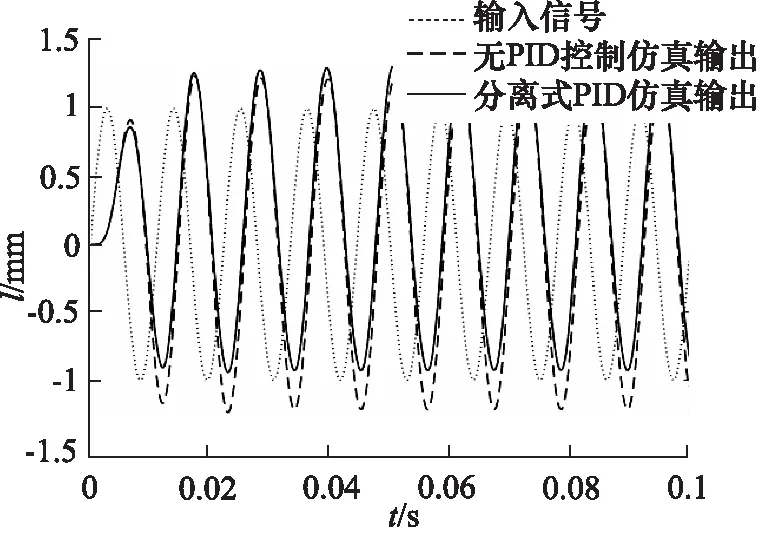
图20 90 Hz分离式PID仿真结果

对系统的瞬态响应性能进行验证。输入单位阶跃信号，输出的结果如图21所示。可以看出，在无PID控制时，系统的超调量大于20%，而加入参数优化后的分离式PID控制后的系统的超调量为5%。故加入参数优化后的分离式PID控制，系统的瞬态响应性能得到了较好地改善。

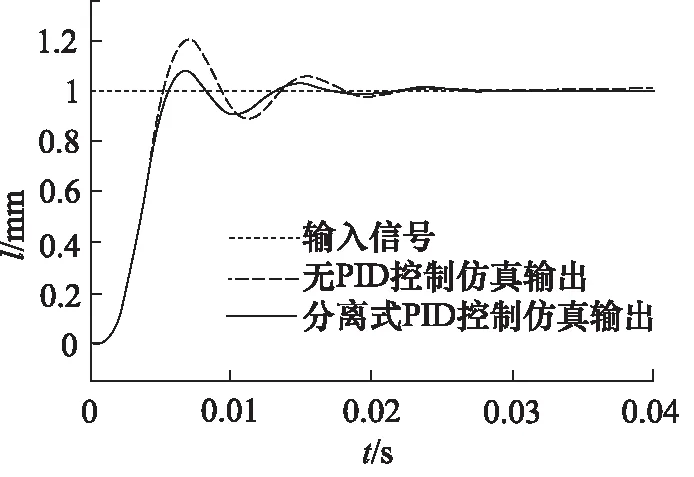
图21 分离式PID阶跃响应仿真结果

3.3 实验验证算法可行性

仿真求解得到两组最优解，通过实验对仿真结果进行验证。

一组为基本PID控制最优参数，用与仿真相同的地震波及频率90 Hz、振幅1 mm的正弦波进行验证，验证结果如图22～图24所示。可以看出，实验结果与仿真结果一致。

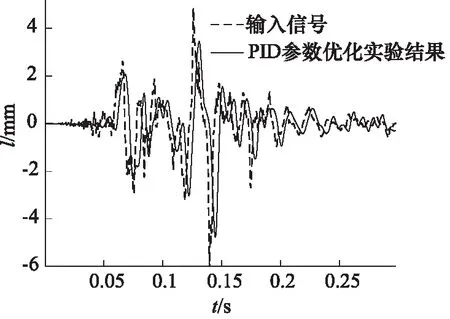
图22 基础PID参数优化实验输出结果

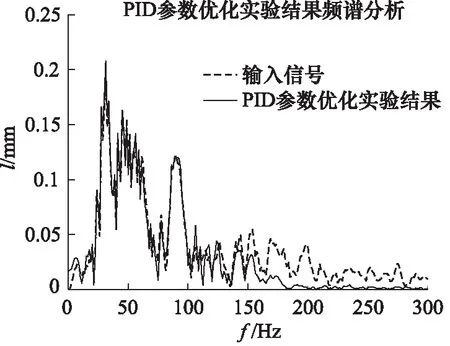
图23 基础PID实验频谱对比分析

另一组为分离式PID控制的最优参数。因为该算法仅对瞬态响应有较好的控制效果，因此用单位阶跃输入对仿真进行验证，实验结果如图25所示。可以看出，仿真的模型与系统真实模型，瞬态性能仍存在一定的差异。但代入最优化参数后的分离式PID控制后，超调量由原先的30%降到了7%，稳定时间由原先的0.11 s降为0.06 s，对系统瞬态响应性能仍有较大的改善。

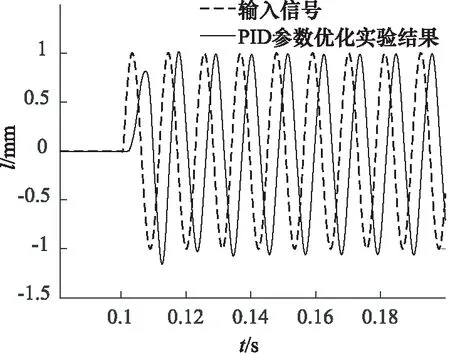
图24 90 Hz正弦波实验结果

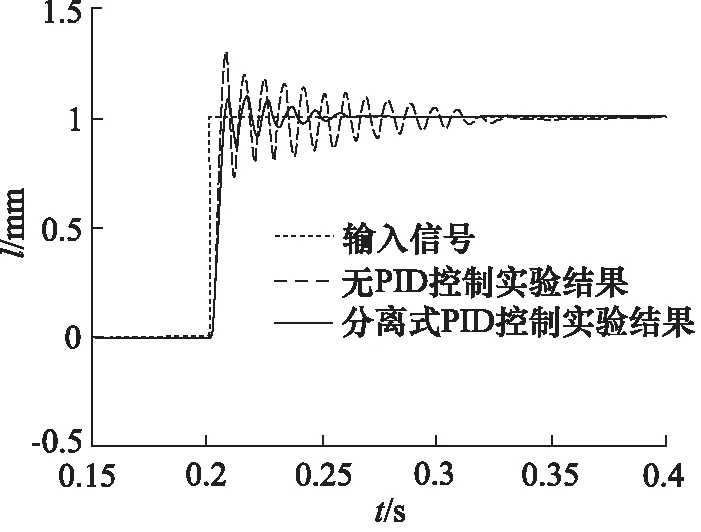
图25 分离式PID阶跃响应实验结果

4 结论

本研究介绍了一种利用MATLAB系统识别与优化函数迭代求解对PID控制参数进行最优调节的方法，并介绍了对基本PID控制器参数的最优调整与对分离式PID控制器的参数调整，可以通过实验结果看出基本的PID控制器的最优解，能够较好地降低系统的谐振峰值， 改善系统中高频的跟踪性能。分离式PID的最优化求解虽然对系统的中高频性能改善不明显，但对于系统的瞬态性能有较为明显的提升。这种基于系统数学模型的PID最优化求解方法适用于大部分工程PID控制器的参数调试，对提高PID控制器参数调试效率有较大帮助，对工程中PID控制器的调试具有普遍借鉴意义。