基于子空间辨识的阀控液压缸泄漏诊断方法
2019-01-25郭隽侠陶建峰刘成良
郭隽侠, 陶建峰, 李 琳, 刘成良
(上海交通大学机械与动力工程学院, 上海 200240)
引言
阀控液压缸作为执行机构在工程机械及工业装备中有着广泛的应用[1]。近年来,有关阀控液压缸泄漏诊断的理论与方法受到高度关注:一方面,液压缸的内泄漏检测是工程实践中的一大难点[2];另一方面,泄漏故障一旦发生而未及时采取有效措施,可能会造成极其严重的后果[3-4]。因此,提出一种有效、及时且便捷的阀控液压缸泄漏诊断方法具有重要的现实意义。
近20年来,国内外学者针对液压系统泄漏诊断进行了大量的研究工作。AN Liang等[5]采用广义卡尔曼滤波方法对液压系统状态进行估计预测,实现了对液压系统不同泄漏类型的故障诊断;邹俊等[6]针对液压泥炮系统泄漏量小、故障频发的特点,将主成分分析(PCA)方法引入到液压泥炮系统的泄漏检测中,有效克服了该系统由于泄漏量小对泄漏诊断产生的不利影响,提高了系统泄漏故障诊断的准确性;周小军[7]将外泄漏和内泄漏分别等效为孔口出流和缝隙流动,采用支持向量机方法提出故障诊断策略,并运用AMESim对相关系统进行了仿真分析;GOHARRIZI AY等[8]研究了Hilbert变换对于液压缸的内泄漏检测的适用性,证明了与第一固有模态函数相关的瞬时振幅的均方根值能够有效地反应液压缸内泄漏及其严重程度,实现了对液压缸小流量泄漏的在线识别;李琳等[9]通过小波分解提取液压缸进口压力信号特征,利用BP 神经网络建立分类器,实现了对液压缸内泄漏的智能识别。这些方法的有效性在实践中已得到验证,但其物理含义通常比较模糊,缺乏直观性。利用子空间辨识方法直接得到液压缸泄漏系数的估计值,进而进行泄漏故障诊断的算法研究几乎仍是空白。
子空间辨识方法综合了几何、线性代数、系统学、滤波理论以及统计学等数学分支思想,能够根据未知系统的输入输出数据获得相关系统参数的无偏估计值,在系统模型辨识中具有数值鲁棒性高、运算速度快、无需模型参数化等诸多优势[10-11],因而被广泛运用于系统建模、预测控制等领域中[12]。对于阀控液压缸泄漏故障,尤其是内泄漏的检测,子空间辨识可根据活塞位移、两腔压力等较易测量的物理量高效、准确地得到阀控液压缸的泄漏情况,且辨识所得的相关参数具有明确的物理含义。
本研究设计了一种基于子空间辨识的阀控液压缸泄漏诊断算法,运用于相关设备在非工作状态下的泄漏检测。对液压缸活塞杆施加轴向外力,测量两腔压力和活塞杆位移,进而由子空间辨识获取缸的内、外泄漏系数。首先,建立典型的阀控液压缸泄漏系统状态空间模型;接着,阐述本研究所采用的子空间辨识算法原理(Multivariable Output Error State Space,MOESP)及主要步骤;然后,提出基于子空间辨识的阀控液压缸泄漏诊断算法流程;进一步,利用MATLAB-Simulink对所提出的算法加以验证;最后,给出算法效果的评价并加以总结。
1 系统原理及数学模型
1.1 系统描述
本研究讨论的阀控液压缸泄漏系统如图1所示。沿液压缸活塞杆轴向的外力驱动活塞杆运动,其负载包括质量、阻尼和弹簧。a,b,c 3处的阀分别模拟液压缸两腔之间的内泄漏与各自的外泄漏。光栅尺用于测量负载的位移,压力传感器用于测量两腔的油液压力。
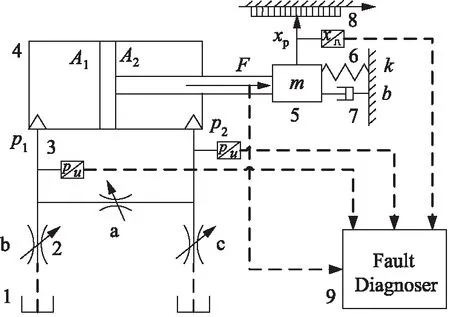
1.回油箱 2.节流阀 3.压力传感器 4.差动液压缸 5.质量块 6.弹簧 7.阻尼 8.光栅尺 9.故障诊断器
1.2 系统假设
针对图1中的系统作如下假设:油液体积弹性模量为常数;液压缸的泄漏均由a,b,c 3处的阀替代,即不存在除a,b,c 3处以外的油液泄漏;不考虑外力突变所导致的瞬时效应;不考虑回油背压的影响。
1.3 数学建模
对于图1给出的系统进行状态空间建模,为此,给出系统所满足的物理方程。
液压缸无杆腔流量连续性方程:
(1)
液压缸有杆腔流量连续性方程:
(2)
式中,A1—— 无杆腔活塞有效面积
A2—— 有杆腔活塞有效面积
V1—— 无杆腔油液体积
V2—— 有杆腔油液体积
Kci—— 内泄漏系数
Kco1—— 无杆腔外泄漏系数
Kco2—— 有杆腔外泄漏系数
E—— 油液体积弹性模量
p1—— 无杆腔油液压力
p2—— 有杆腔油液压力
xp—— 活塞位移
考虑到活塞杆上的惯性、阻尼、弹簧负载,其力平衡方程为:
(3)
式中,F—— 外驱动力
m—— 负载质量
b—— 系统阻尼系数
k—— 负载弹性模量
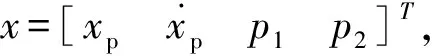
(4)
式中,
由于实际过程中,传感器测得的位移与压力信号均为离散时间信号,因而将式(4)转化为离散时间形式。设采样周期为τ,并采用欧拉法近似替代状态变量的一阶导数,得到系统的离散时间状态空间表达式:
(5)
式中,
2 子空间辨识及故障诊断
2.1 子空间辨识方法
本研究的阀控液压缸泄漏模型为四阶开环离散时间系统,采用子空间辨识理论中经典的MOESP方法[13],由系统输入、输出量得到原系统矩阵Ad经线性变换后的矩阵AdT。
本节阐述对于一般离散系统的MOESP辨识算法,假设系统状态空间模型为:
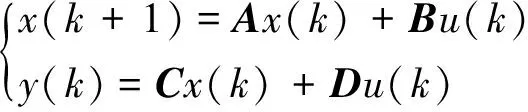
(6)
式中,x(k)∈Rn,u(k)∈Rm,y(k)∈Rl,n,m,l均为正整数,k=0,1,2,…。若系统初值为x(0),则由式(6)可得:
x(1)=Ax(0)+Bu(0)
x(2)=A2x(0)+ABu(0)+Bu(1)
⋮
(7)
类似地,对于系统输出有:
y(0)=Cx(0)+Du(0)
y(1)=CAx(0)+CBu(0)+Du(1)
y(2)=CA2x(0)+CABu(0)+CBu(1)+Du(2)
⋮
y(k)=CAkx(0)+CAk-1Bu(0)+CAk-2Bu(1)+
…+CBu(k-1)+Du(k)
(8)
将式(7)、式(8)写成矩阵形式,则有:
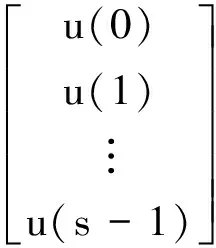
(9)
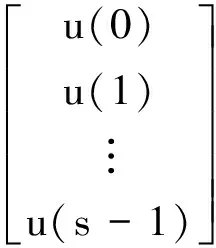
(10)
式中,s>n且为正整数。定义:
Yi,N=[y(i),y(i+1),…,y(i+N-1)]∈Rm×N
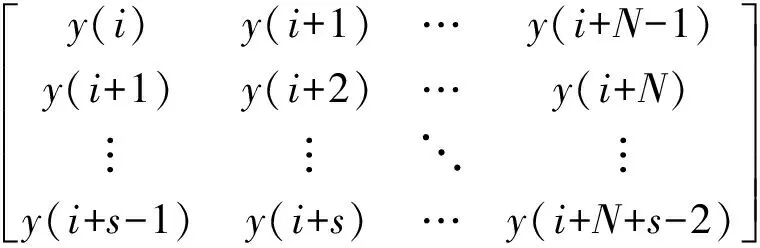
N为正整数。类似地,定义Xi,N,Ui,N与Ui,s,N。同时,定义:
则式(10)可简写为:
Y0,s,N=ΓsX0,N+Hu,sU0,s,N
(11)
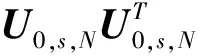
其中,IN为N阶单位矩阵,显然:
(12)
则式(11)转化为:
(13)
(14)
式中,Q1,Q2,Q3均为正交矩阵,则:
R11Q1=R22Q2
(15)
由于Q2是正交矩阵,因此R22与Γs的列空间等价,rank(R22)=n。设R22的SVD分解为:
R22=Un∑nVn
(16)
其中,Un,Vn均为正交矩阵,∑n为对角矩阵且对角线元素为R22的n个特征值。由矩阵理论知,Un的各列为矩阵R22列空间的一组标准正交基,因而Un可看作Γs经某一线性变换后的矩阵,即存在可逆矩阵T,使得:
(17)
其中,CT=CT,AT=T-1AT。
由式(17)可知,Un的前l行即为CT,而AT可由下式求得:
Un(1∶(s-1)l,1∶n)AT=Un(l+1∶sl,1∶n) (18)
2.2 阀控液压缸泄漏诊断算法
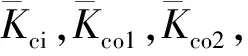
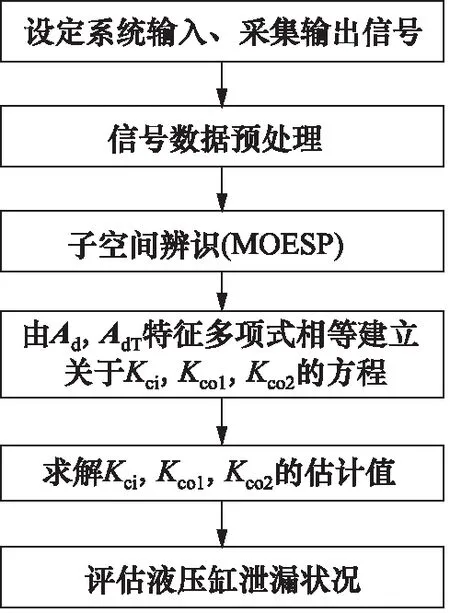
图2 泄漏诊断流程
3 算法验证
在MATLAB/Simulink平台搭建系统仿真模型,对提出的阀控液压缸泄漏诊断算法加以验证。所搭建的仿真系统采样周期τ=5×10-5s,仿真时长1 s,初始状态x(0)=[0 0 1×1072×107]T。在初始状态时,活塞在外驱动力的作用下处于平衡状态,外驱动力为恒力F=1000 N,并在活塞位移输出中引入20 dB的高斯白噪声,系统其他相关参数如表1所示。
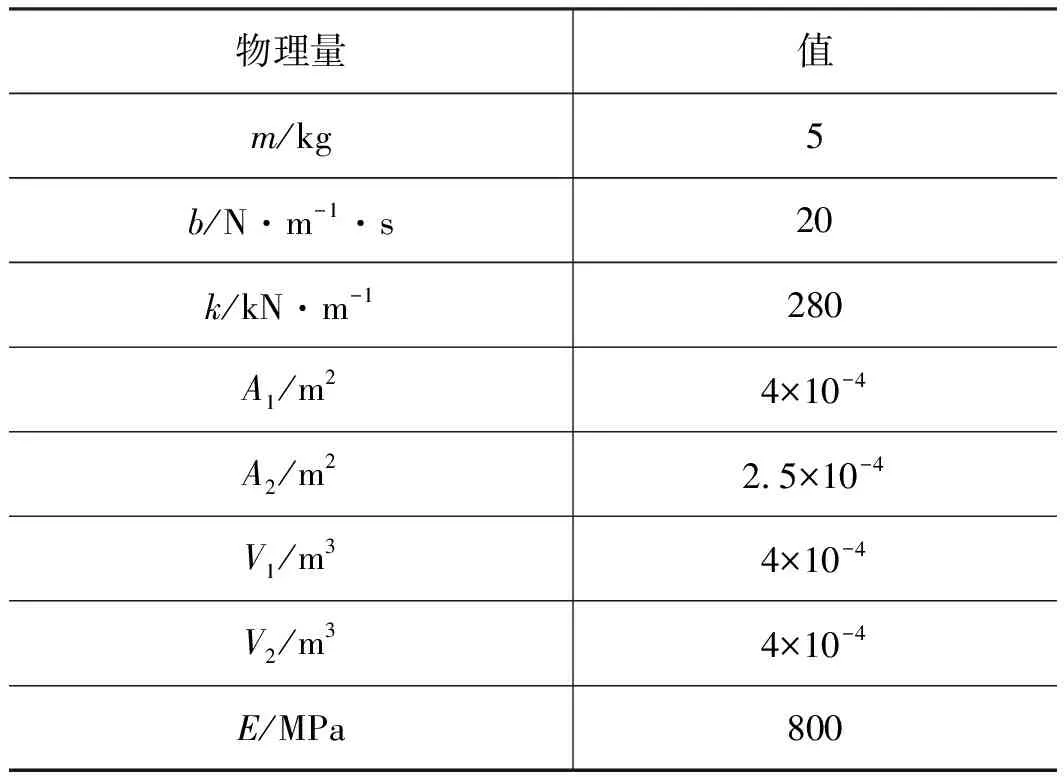
表1 仿真系统参数
将Kci为0.12 mL·min-1·MPa-1,Kco1为0.06 mL·min-1·MPa-1,Kco2为0.06 mL·min-1·MPa-1作为无泄漏基准状态,认为系统产生小泄漏故障时各泄漏系数增大为基准值的5倍,即出现小内泄漏时Kci为0.6 mL·min-1·MPa-1,出现小外泄漏时Kco1为0.3 mL·min-1·MPa-1,Kco2为0.3 mL·min-1·MPa-1;认为系统产生大泄漏故障时各泄漏系数增大为基准值的100倍,即大内泄漏时Kci为12 mL·min-1·MPa-1,大外泄漏时Kco1为6 mL·min-1·MPa-1,Kco2为6 mL·min-1·MPa-1。
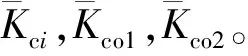
4 结论
本研究提出了一种基于子空间辨识的阀控液压缸泄漏诊断算法。建立阀控液压缸系统的状态空间模型,阐述所采用的MOESP子空间辨识原理,并提出诊断算法流程。MATLAB-Simulink仿真及运算结果表明,提出的算法能够准确得到系统内、外泄漏系数的估计值,实现了对于阀控液压缸泄漏故障的有效诊断。
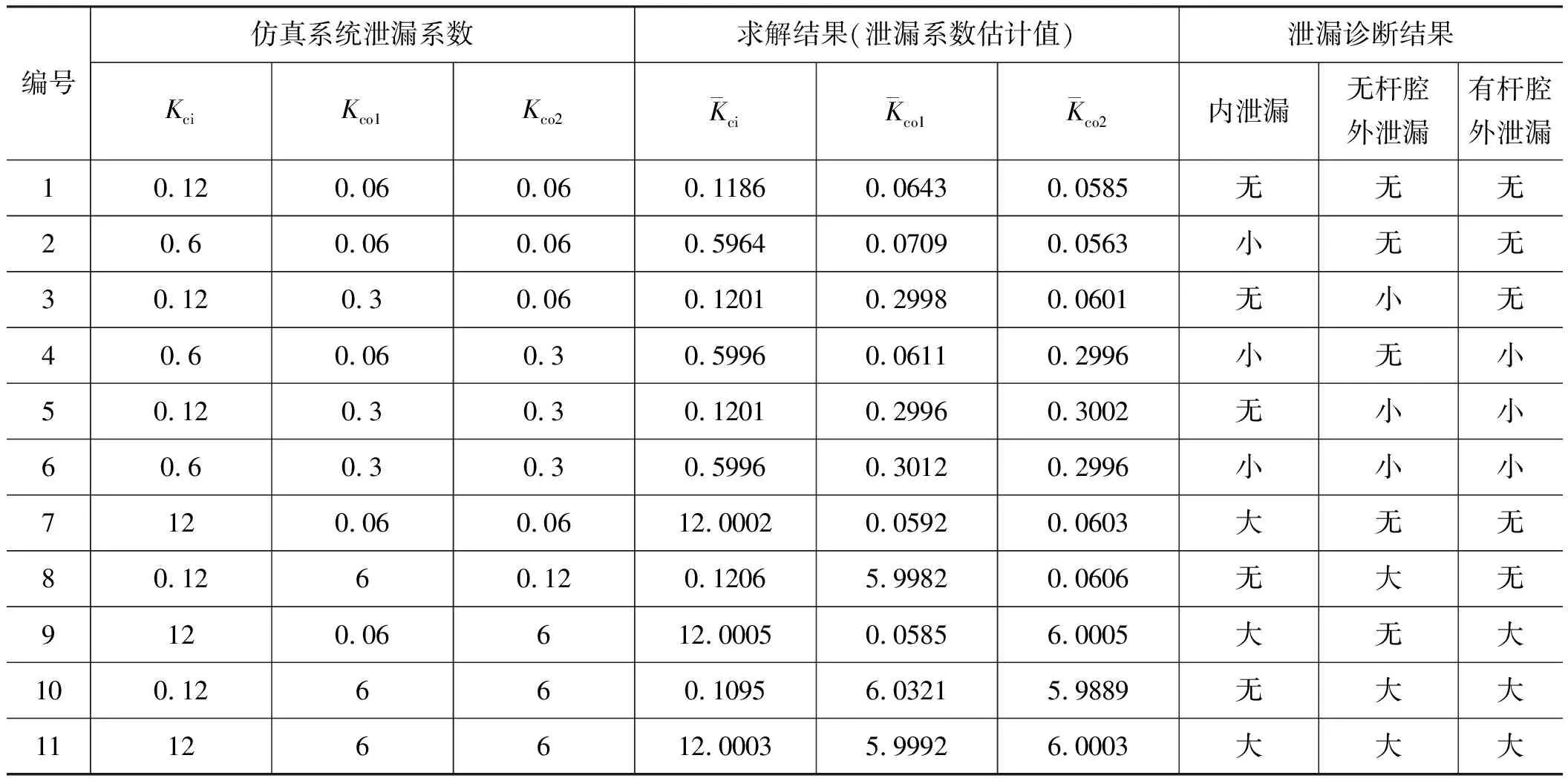
表2 泄漏系数求解及诊断结果 mL·min-1·MPa-1
