PSS2A模型在水泥余热机组励磁中的实现与应用
2020-12-18邓国平中国中材国际工程股份有限公司江苏南京211100
邓国平(中国中材国际工程股份有限公司,江苏 南京 211100)
1 PSS2A模型
PSS(Power System Stability),也就是通常所说的电力系统稳定器。典型的PSS2A数学模型在IEEE STD421.5中有详细的传递函数描述见图1。
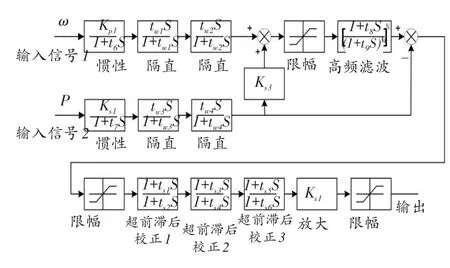
图1 典型的PSS2A数学模型在IEEE STD421.5中详细的传递函数描述
通常励磁调节器通过电压闭环的PID方式进行控制,由于转子磁场的惯性时间常数的滞后,产生了不利于机组稳定运行的负阻尼。PSS2A辅助功能的作用就是通过以频率(转速)与功率为输入信号,它们分别经过传递函数中所规定的超前、滞后环节,最后产生一个叠加(辅助)的控制信号到PID的闭环中给定值,使励磁系统为机组的稳定运行提供正阻尼。
2 PSS2A模型在控制程序中的处理
连续系统传递函数常用拉普拉斯变换来描述,而实现该传递函数的微机化(数字控制系统),那就必须使用到离散处理(Z变换)。从图1中PSS2A所描述的传递函数,主要有几个典型的子环节:惯性环节、超前滞后环节、隔直环节、高频滤波环节、线性放大环节、限幅环节。由于线性放大环节和限幅环节相对比较简单易懂,本文不再描述处理过程。本文着重介绍隔直环节与惯性环节的离散化处理,其余的几个环节,也都是按类似描述的过程进行相应的处理。
(1)隔直环节。
传递函数为:

输入输出的为:
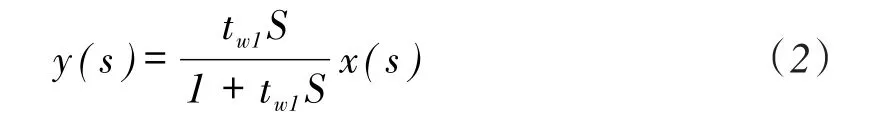
传递函数变为:
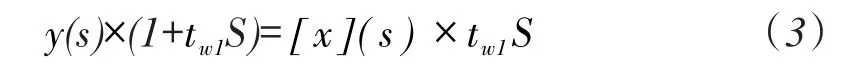
时域离散为:
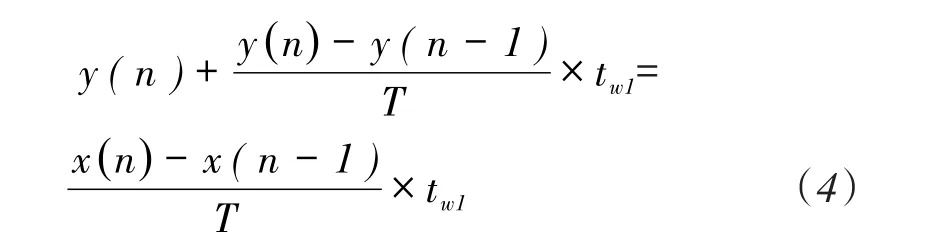
可得到:
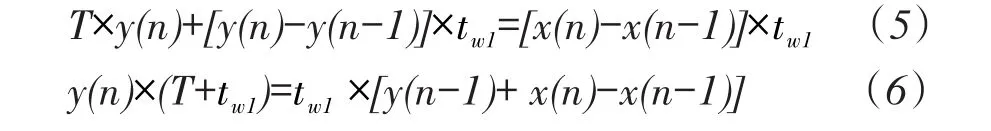
其中:y(n)—传递函数的本次输出,y(n-1)—传递函数的上次输出;x(n)—传递函数的本次输入,x(n-1)—传递函数的上次输入,T—采样周期,tw1—时间常数。
隔直环节程序处理:

(2)惯性环节。
传递函数:

输入输出的为:

传递函数变为:

时域离散为:
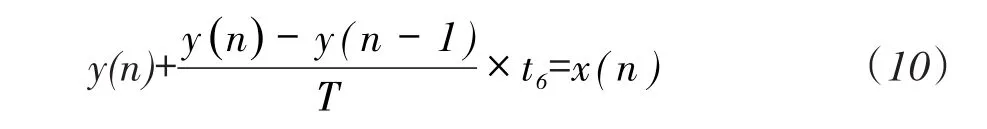
由上式可得到:
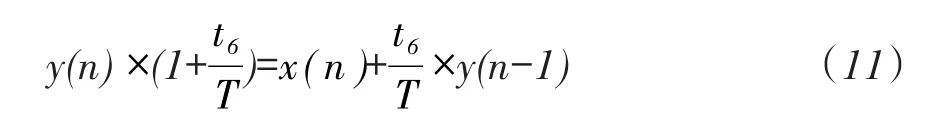
其中:y(n)为传递函数的本次输出,y(n-1)为传递函数的上次输出;x(n)为传递函数的本次输入;T为采样周期,t6为时间常数。
惯性环节程序处理:

(3)超前滞后环节。
传递函数:

输入输出的为:

传递函数变为:
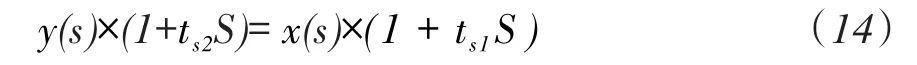
时域离散为:
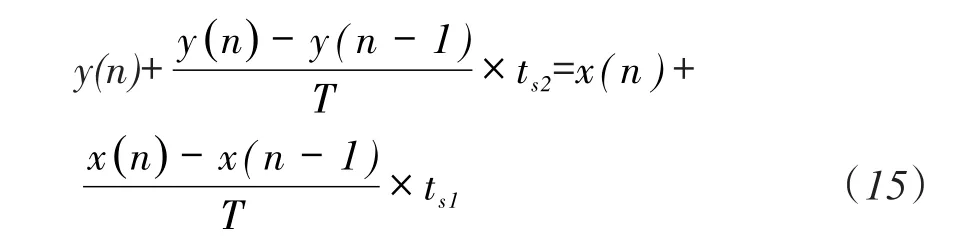
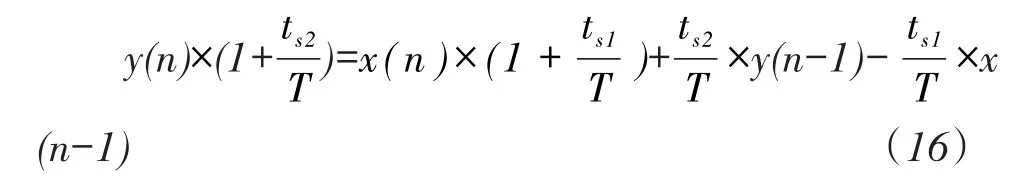
其中:y(n)—传递函数的本次输出,y(n-1)—传递函数的上次输出;x(n)—传递函数的本次输入,x(n-1)—传递函数的上次输入;T—采样周期,ts1、ts2—时间常数。
超前滞后环节程序处理:

可得到:

(4)高通滤波环节。高通滤波环节的参数,IEEE推荐M=5,N=1。实际上也就是在一阶超前滞后环节滞后,再加四个惯性环节处理,达到同样的结果。其离散化过程也是与上面介绍的一致,此处不再赘述了。
程序是循环执行的,一个变量在赋新值前,就是上次计算的历史值,当然,为了程序的可读性与易读性,我们在程序中也用new和old来定义与区分历史值与当前新的数值。
3 云南凤庆习谦水泥机组并网后的试验
关于PSS定值和效果验证,我们在云南凤庆习谦水泥余热机组进行了试验。PSS试验首先在100%、90%额定有功的两个工况下分别测试了机组励磁系统相频特性,据此计算了PSS有关参数,之后在上述工况下验证PSS在本文提供的整定值下对有功振荡的阻尼效果。在习谦水泥厂余热发电机组中,分别测试参数、设置参数、并网状态下做电压4%的阶跃实验,分析录波曲线并做结论评判,见表1,图1,图2。
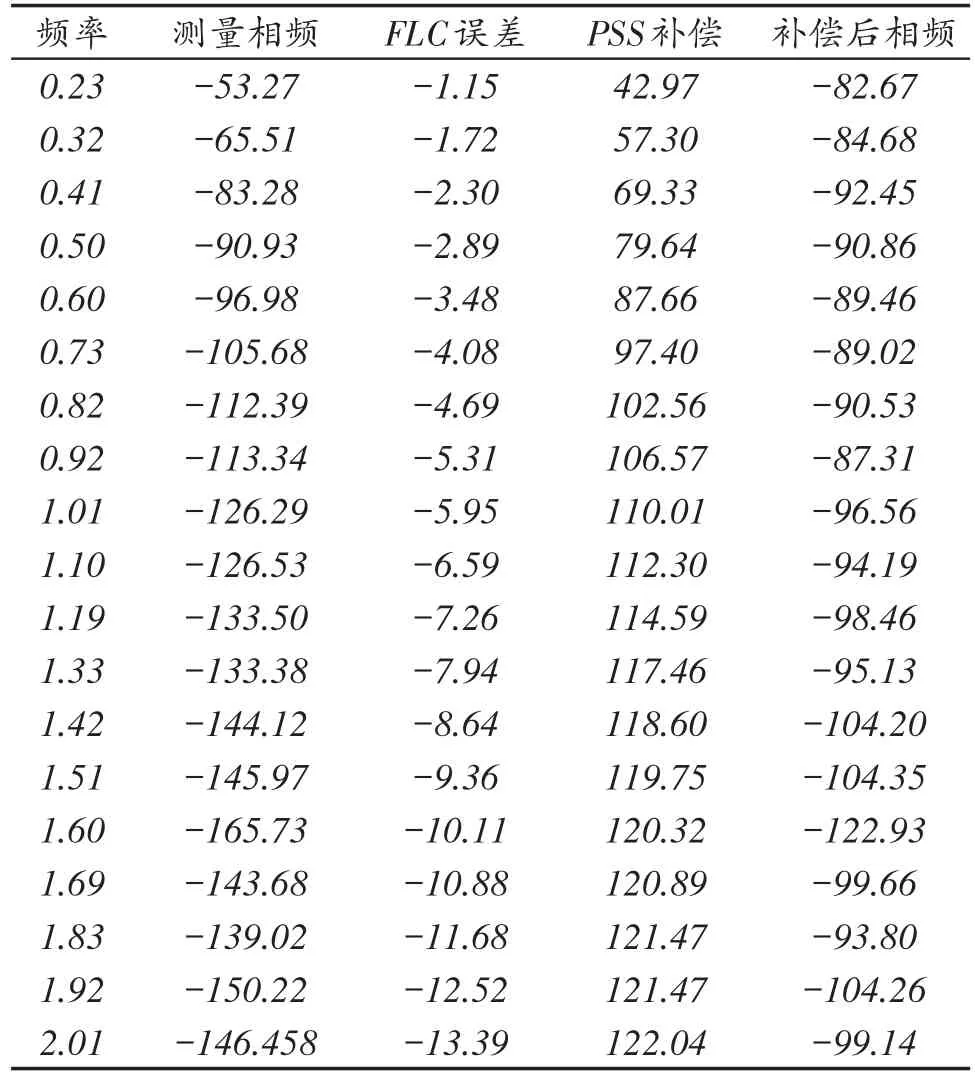
表1 机组相频特性 Hz
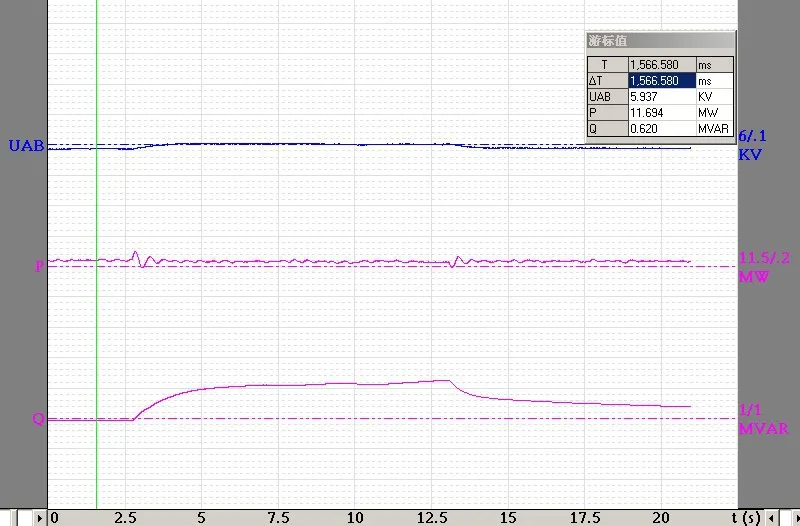
图1 P=Pe,PSS退出,4%阶跃
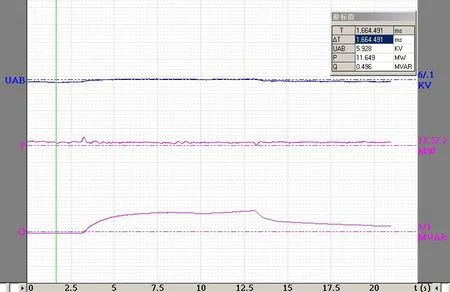
图2 P=Pe,PSS投入,4%阶跃
机组PSS整定的定值为:
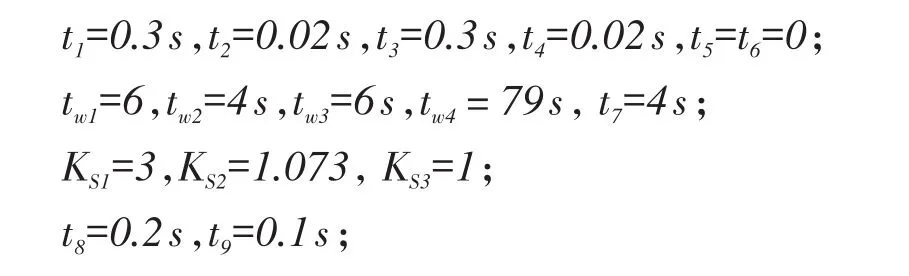
PSS出口限幅为±10%;PSS投退有功水平为30%Sn;PSS临界增益为KS1=8。
3 结论
以PSS2A模型实现的功能在水泥余热机组中的使用,对抑制系统低频振荡(0.2~2Hz)有明显的效果,振荡周期由2~3个减少到0.5~1个,提高系统的动态稳定性。
