力干扰下的电液位置系统自适应鲁棒控制

李 旭， 芮光超， 殷士才， 汤 裕， 沈 刚

(1. 中国船舶重工集团公司第七一三研究所， 河南郑州 450000；2. 河南省水下智能装备重点实验室， 河南郑州 450000； 3. 中国矿业大学机电学院， 江苏徐州 221116)

引言

电液伺服系统广泛应用于各大领域[1]，主要用于研究被控对象的位置[2]运动状态和力加载[3]状态，从而实现整个电液系统控制功能[4]。

电液伺服系统中依照控制理论输出所要求的控制信号来对其进行控制，最终得到满足需求的输出信号，并且使得系统同时具有响应稳定、 抗干扰性强和输出结果精确等能力[5]。在实际操作处理的过程中，所要控制对象的模型复杂[6]，而且系统中还有非线性[7]、外界干扰[8]和参数时变[9]等因素影响整个控制。传统的控制系统通常可以视为一个比较容易简化而且可线性化建模[10]的控制系统，但是几乎很难用描述系统状态空间和传递函数的方法来真实而有效地反应系统确切状态[11]，这就要求在控制方法理论上进行更为贴近实际系统的研究和探索[12]。

为了确保系统的跟踪特性，在提高系统精度的同时也需要对外界的干扰进行抑制[13]。一些专家对于电液伺服系统中存在的不确定性参数，提出了一种非线性的自适应控制方法[14]，如对伺服系统控制的影响。然而精确反馈自适应控制对伺服系统的模型精度要求很高，在实际中实现比较困难。

为了抑制外界存在的未知干扰，可以将非线性观测器与反步滑模等算法相结合。国内外的学者研究了许多干扰观测器用以对外界的干扰进行抑制。因此可以发现干扰观测器可以对外界的位置干扰有很好的抑制[15]。

综上所述，当外界存在较大的干扰时，电液系统的精度及稳定性有很大下降，为了进一步改善控制器性能，将耦合系统互相作用当成干扰来处理，对干扰进行抑制，进而提高系统的鲁棒性，本研究设计了一种自适应鲁棒控制器，实现对干扰的抑制。

1 系统的非线性数学模型

如图1所示，该系统使用阀控对称液压缸。在建立流量方程时，假设此阀为零开口阀、供油压力ps为常值、回油压力p0为0。

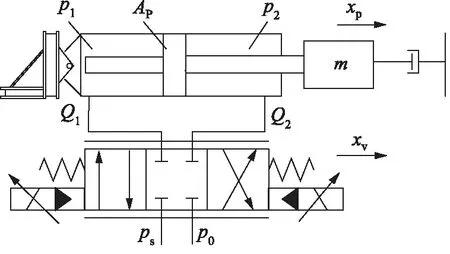
图1 液压动力机构

忽略压缩流量，流量方程为：

QL=Kqxv-KcpL

(1)

式中，Kq—— 滑阀的流量增益

Kc—— 滑阀的流量压力系数

pL—— 负载压降，定义pL=p1-p2

液压缸的流量连续性方程：

(2)

式中，Ap—— 液压缸活塞的有效面积

xp—— 活塞位移

Ctp—— 液压缸的总泄漏系数

Vt—— 液压缸中两腔的总容积

βe—— 有效体积的弹性模量

忽略流体的质量和摩擦，系统的力平衡方程为：

(3)

式中，m—— 活塞和负载折合到活塞上的总质量

Bp—— 活塞和负载的黏性阻尼系数

FL—— 作用在负载上的外负载力

为了采用自适应鲁棒法对电液系统进行控制，首先需要将其写成系统状态方程，根据自适应鲁棒控制器的控制原理，考虑外界干扰和参数不确定性的建模如下：

(4)

式中，D为外界未知干扰。

2 控制器设计

2.1 非线性观测器的设计

设计的非线性干扰观测器如下：

(5)

式中，p(x1,x2) —— 待设计的非线性函数

L(x1,x2) —— 非线性观测器的增益

两者满足关系如下：

(6)

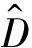
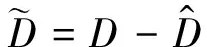
(7)

对等式两端进行微分，得：

=L(x1,x2)(z+p·(x1,x2))-

(8)

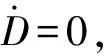
令L(x1,x2)=b,b>0，有：

p(x1,x2)=bx2

(9)

2.2 自适应反步控制器的设计

设计的自适应反步控制器系统，其中α1，α2定义为虚拟控制量，定义3个误差信号：

(10)

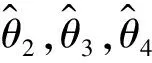
(11)

(1) 步骤1

令误差e1接近于0，函数定义为：

(12)

求导函数两端，代入系统的状态方程：

(13)

可使虚拟控制量为：

其中,k1为大于0的正数。则虚拟控制量的导数为：

(14)

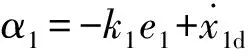
(2) 步骤2

令e2接近于0，且考虑参数θ2的存在，函数定义为：

(15)

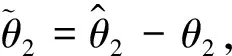
(16)

可使虚拟控制量为：

(17)

其中，k2为大于0的正数。所以有:

(18)

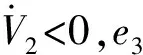
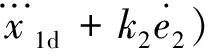
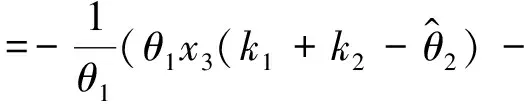
(19)

在下面的推导中，主要是提取θ2其中不确定的部分，通过自适应的方法将它消除，所以可令α2的导数为：

(20)

其中，

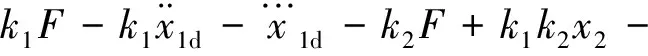
(21)

(3) 步骤3

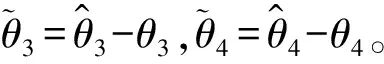
(22)

求导函数两端，代入系统的状态方程：

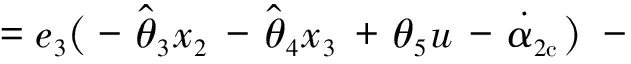
(23)

从式(22)中已经能够计算出控制的输入信号，得：

将控制的输入信号带入式(22)可得：

(25)

为了消除参数变化带来的偏差，取自适应率如下：

(26)

代入式(24)得：

(27)

如图2是自适应鲁棒控制器的原理图，利用观测器将外界的干扰D输入到反步控制器中，实现最终的干扰抑制补偿。

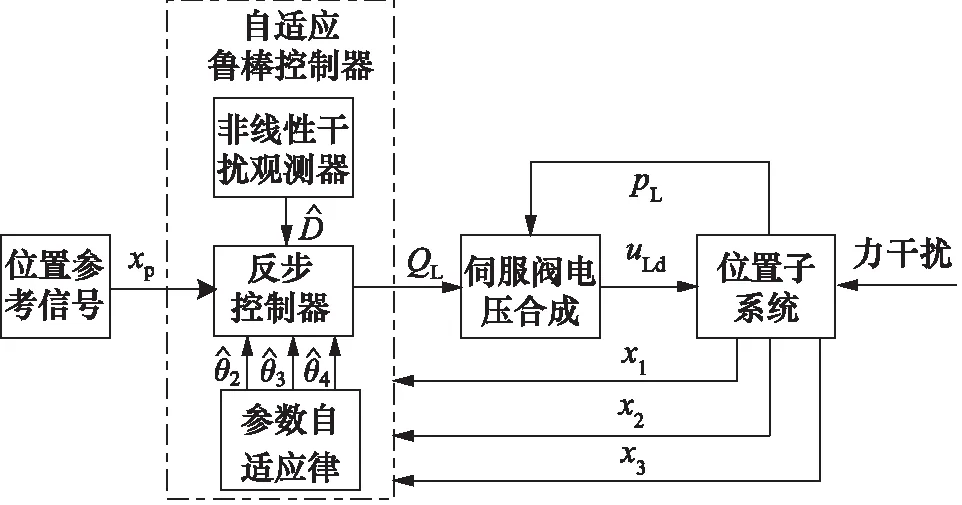
图2 系统控制方案

根据李雅普诺夫理论，可知整个系统是稳定的。至此，设计的电液位置伺服系统的自适应鲁棒控制器完成，即在原来的反步控制中加入了干扰观测器和自适应控制的方法。系统通过抑制干扰的方法对电液伺服系统的力位耦合特性进行改善，对整个控制系统的鲁棒性有了很大的提高。

3 试验验证

3.1 试验台

如图3所示，振动台、液压缸、伺服阀和泵站组成了整个试验台。振动台用于安装测试件或相关设备，并通过铰支座连接到液压缸，试验台相关参数如表1所示。

图3 试验台

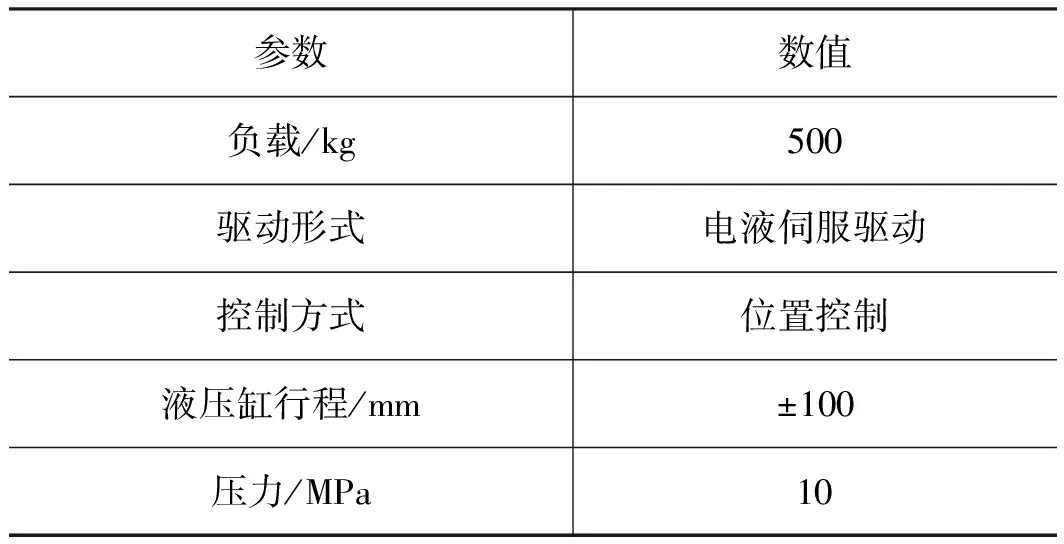
表1 试验台主要参数

图4为控制原理图，整个系统的位置闭环由指令信号经控制算法产生的位移信号以及振动台位置变化的输出信号构成；控制器输出-10～+10 V的驱动信号，然后由ACL-6126板卡进行发送，由信号调理电路和功率放大器产生-40～+40 mA的电流信号，以驱动电液伺服阀的运动。根据激励信号，伺服阀控制振动台进行相应的运动。

图5为实验控制程序，其中自适应鲁棒控器：反步系数k1=230，k2=150，k3=60，γ2=1×10-11，γ3=4000，γ4=1×10-15，干扰观测器的参数b=500。

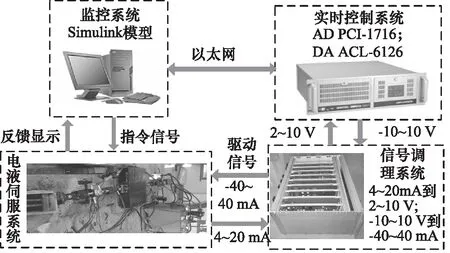
图4 试验台控制原理

3.2 试验结果

首先，在只有PID控制的情况下，输入一组随机信号，并且在负载的另一端施加未知的干扰力，得到如图6所示的跟踪曲线，可以发现其幅值相位都有很大的偏差。然后，在相同的随机信号和干扰力下切换到反步控制器，得到如图7所示的跟踪曲线，可以发现其幅值相位都得到了很好的改善，但是仍然受到的外界干扰的影响。最后，切换到自适应鲁棒控制器，得到的跟踪曲线如图8所示。对比不同控制器的信号跟踪曲线可以看出，精度有很大的提高，表明自适应鲁棒控制器对外界干扰具有很好的抑制效果。图中X为缸的位移信号。

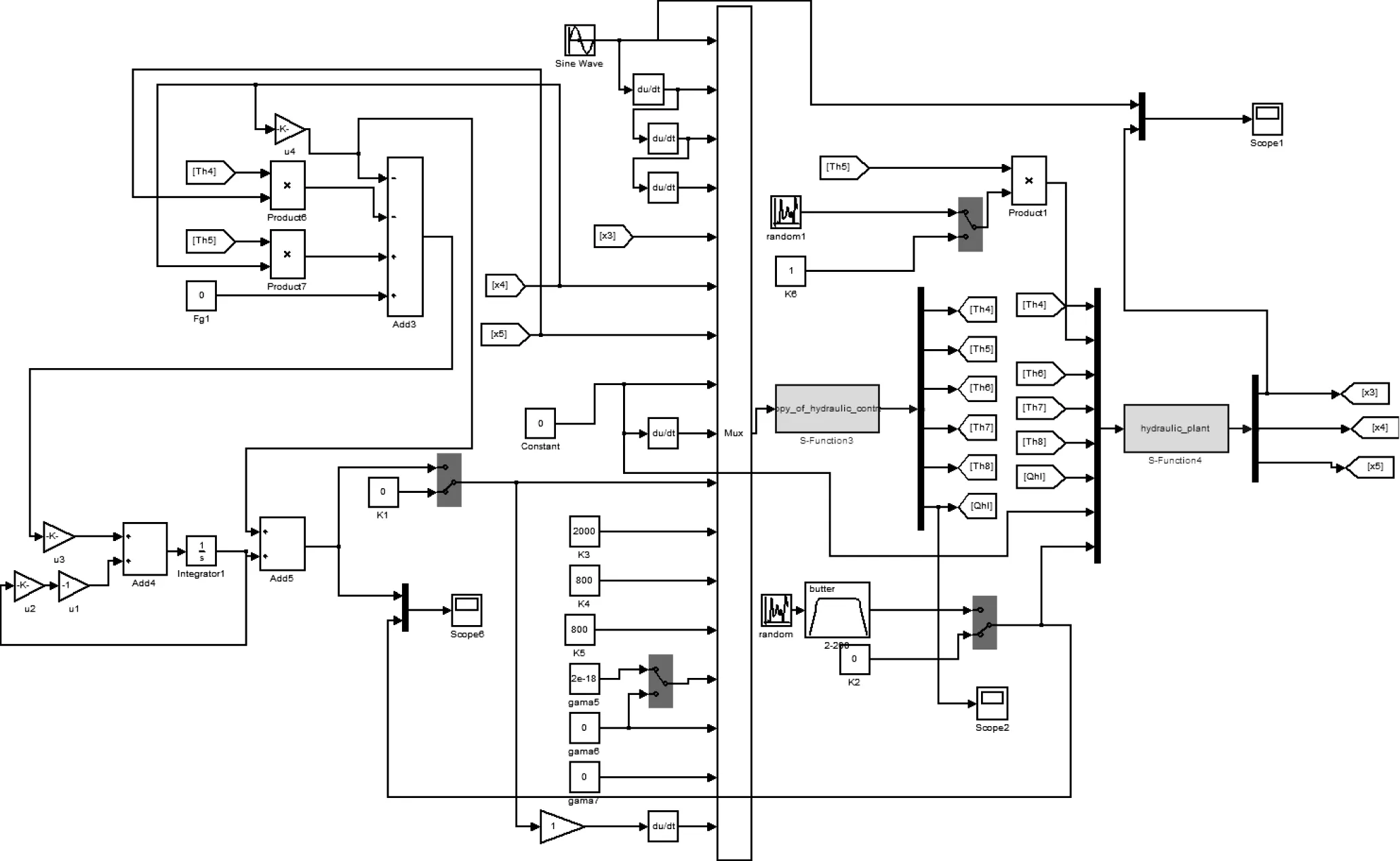
图5 实验控制程序

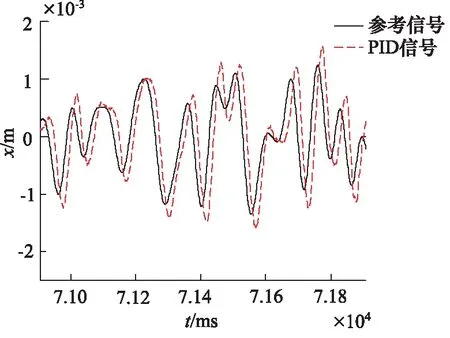
图6 PID控制器跟踪曲线

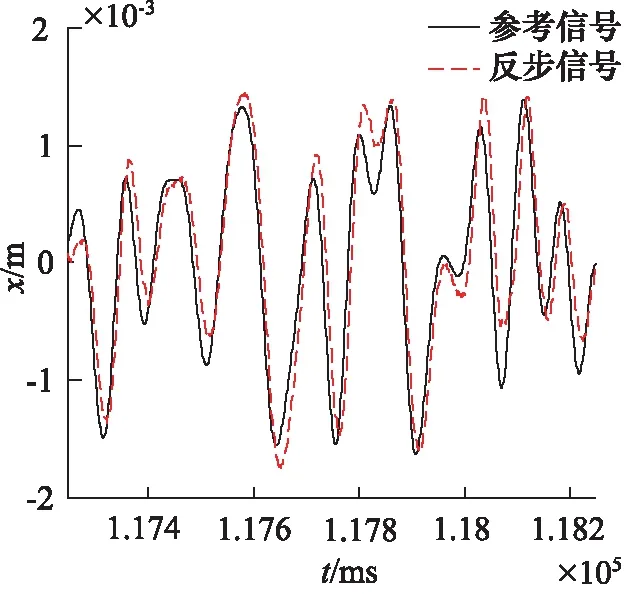
图7 反步控制器跟踪曲线

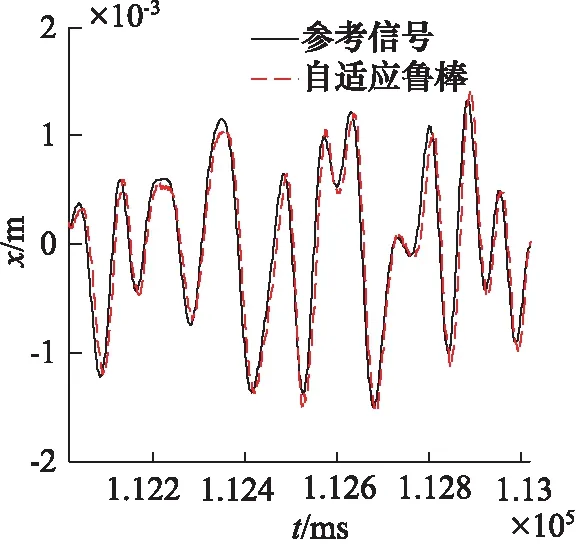
图8 自适应鲁棒控制器跟踪曲线

4 结论

从有干扰情况下的随机信号的试验可以得到，提出的基于反步控制的非线性策略要比传统PID控制效果更好，对于干扰能够有效的抑制。反步控制器和自适应鲁棒控制器的跟踪效果，后者在反步控制器的基础上增加了干扰观测器和自适应参数的控制方法，进一步改善了控制效果。试验结果显示，所提出的控制策略有效抑制了外界干扰力对电液伺服系统的影响，对电液伺服系统的跟踪精度有很大的提高，所以该控制策略是切实可行的。