基于稀疏先验正则化的图像盲去模糊

肖 宿

（淮北师范大学计算机科学与技术学院 安徽淮北 235000）

一、引言

图像盲去模糊（BID，blindimagedeblurring）易受不适定性干扰，会严重降低复原图像的质量。因此，对未知清晰图像和模糊核应选择合适的先验假设，以稳健高效地获得令人满意的图像去模糊结果。在过去几十年间，基于稀疏先验的图像处理研究取得了丰硕的成果，产生了许多具有代表性的方法[1-6]。为充分利用稀疏性，在图像盲去模糊模型中，常以未知清晰图像和模糊核或其稀疏变换的lp范数（0≤p≤1或p=2）充当模型罚函数的正则项，以提高图像盲去模糊的能力。因为l2范数不能严格地满足稀疏条件，新提出的方法很少对未知清晰图像和模糊核或其稀疏变换施加l2正则化，以防止生成过于平滑的清晰图像。显然，考虑到图像盲去模糊的结果，主流的方法更倾向于使用lp范数正则化（0≤p≤1），比如l0范数正则化和l1范数正则化。虽然，以非凸l0范数作为正则项时，图像盲复原模型变为NP-hard问题，但l0范数正则化仍然是诱导稀疏性最直接方法，因为它直接计算非零值的数量。作为l0范数的等效松弛，凸l1范数越来越受到欢迎，因为处理l1范数正则化问题很容易获得其解析解。但只有当最终解足够稀疏时，l1正则化和l0正则化之间等效性才有效。最近，lp范数正则化（0〈p〈1）引起了越来越多的关注，并在图像盲去模糊中获得了更多的应用，因为它有助相应方法复原出自然图像[7]。尽管当p趋近零时，l0范数可被视为lp范数的极限情况。但相比较而言，lp范数（0〈p〈1）相关的问题更难处理。值得注意的是，绝大多数自然图像虽然是非稀疏的，但根据稀疏表示理论，可以通过变换（例如，框架波变换）对图像进行编码以稀疏地表示它们。因此，lp范数（0≤p≤1，p=2）通常被用于图像的变换系数而非图像本身。

在陈繁昌等人[8]建立的全变分盲去模糊（TVBD，total variationblinddeblurring）模型中，l1范数被用于刻画未知清晰图像和模糊的梯度稀疏性，以实现稀疏正则化。在快速傅里叶变换域中，使用共轭梯度迭代计算TVBD模型的欧拉-拉格朗日（EL，Euler-Lagrange）方程，以交替估计未知清晰图像和模糊核。因直接计算EL方程的效率低，因此Li等人[9]建议采用分裂Bregman迭代处理TVBD模型，从而显着减少了计算开销。为了改进文献[8]的工作，Liao等人[10]提出用模糊核的拉普拉斯算子l2范数替换TVBD模型中模糊核的TV-l1范数。因为正则化参数也会影响恢复质量，作者还引入广义交叉验证对其自动选择。受变量分裂（VB，variablesplitting）应用的启发，文献[10]采用与之类似的方法处理清晰图像估计子问题。考虑到自然稀疏性，胡哲等人[11]应用拉普拉斯算子l2范数对模糊核正则化，并利用了图像的变换稀疏性而非梯度图像的稀疏性，即清晰图像首先表示为预定义字典和对应的稀疏的乘积，然后变换系数的l1范数被用作正则项。蔡剑锋等人[12]也将分裂Bregman迭代应用于清晰图像重建和模糊核估计。为了保持估计模糊核的连续性和稀疏性，使用框架波系统下未知模糊核稀疏表示的二次l2范数和l1范数对其正则化。其中，l1范数正则化可避免由模糊核估计产生的误差干扰。当采用分裂Bregman来解决BID问题时，原问题通常分解为更容易子问题加以处理。张海潮等人[13]提出一种联合方法同时估计模糊核，恢复清晰图像和面部识别。为了利用稀疏先验改进BID，使用训练字典稀疏地表示清晰图像，并以产生的变换系数的l1范数和未知清晰图像梯度的lp范数（p=0.5）作为正则项。通过快速傅里叶变换，多尺度估计方法和稀疏投影交替地求解其建立的BID模型。邵文泽等人[14]将混合l1范数和二次l2范数正则化应用于清晰图像和模糊核以改善BID。通过融合变量分裂和增广拉格朗日方法，交替迭代地执行清晰图像重建和模糊核的估计。基于图像梯度和暗通道稀疏先验，潘金山等人[15]为未知的清晰图像提供了一种混合的l0范数正则化，以获得令人满意的图像盲去模糊结果。二次l2范数正则化被用于模糊核，将模糊核估计简化为可直接求解的最小二乘子问题。为利用稀疏边缘先验，Almeida等[16]对清晰图像梯度和模糊核分别进行lp范数（p=0.4）正则化和l1范数正则化。使用带连续策略的交替优化过程导出图像去模糊问题的局部最小解。Amizic等人[17]分别对清晰图像及其变换系数的二阶差分执行lp范数正则化和l1范数正则化，并使用拉普拉斯算子l2范数来正则模糊核[10],[11]。通过优化-最小化（majorization-minimization）和压缩感知重建方法交替处理子问题以获得估计的清晰图像，模糊核和变换系数。

本研究的重点是通过分裂交替最小化（SAM，split alternating minimization），广义软阈值（GST，generalized soft-thresholding）函数和快速傅里叶变换等来解决BID问题。为了消除不适定性的不利影响，构造一个新的含稀疏lp范数正则化的BID模型。SAM将所建立的模型解耦为可迭代交替处理的子问题，这些子问题可以通过快速傅里叶变换和GST等有效地计算。在标准测试图像上进行实验以评估所提出方法的有效性和性能。

二、本文提出的BID方法

对于图像退化，BID旨在按照期望由给定的模糊图像估计清晰图像和模糊核。设y，k和x分别代表观察到的模糊图像，未知模糊核和未知清晰图像。图像退化可以表示为

其中，“★”表示卷积运算，n是加性噪声。从数学的角度看，BID问题属于求逆问题，亦属于不适定问题，因此，式(1)通常不存在唯一解。为了求解BID问题一般将其纳入正则化框架，以使其适定化，从而BID问题模型可统一表示为

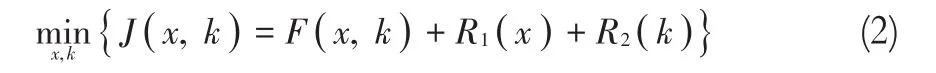
其中，J(x,k)是罚函数；F(x,k)是数据拟合项；第二和第三项是正则项，它们分别代表对清晰图像和模糊核的先验约束。在过去十余年中，稀疏先验在图像处理领域取得了巨大成功。因此，它们现在被视为许多正则化BID方法的首选。

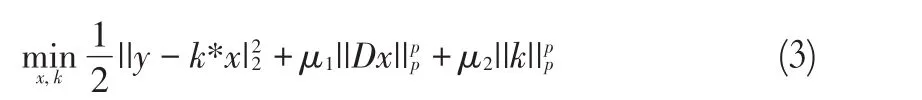
本研究的重点是解决稀疏先验正则化BID问题，以有效地重建清晰图像和估计模糊核。基于式(2)，我们将BID问题建模为其中，数据拟合项惩罚y和k*x之间的距离；和是稀疏性促进正则算子；参数μ1和μ2是大于零的常数；D是变换算子（例如，冗余小波变换）。在由D表示的变换域中，x可以被编码为稀疏系数，即Dx是稀疏的；||·||p是lp范数，p的取值范围[0,1]，它有助于消除异常值和微小细节。对于信号z，其lp范数可以写成

其中，zi表示z的某个元素。直接计算式(3)是行不通的，因为该式的罚函数包含两个未知的参数和相应的lp范数。为解决这个棘手的问题，建议采用SAM方法，即交替最小化迭代（AMI，alternating minimization iteration）加VB。

SAM将问题(3)等同于下面两个交替迭代的问题：

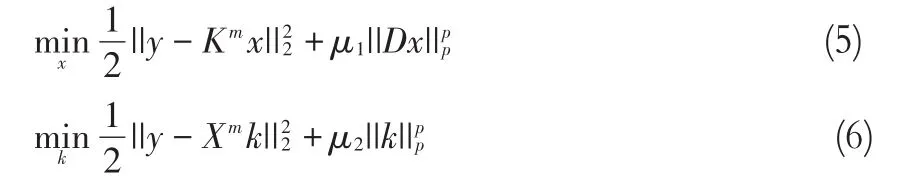
其中，Km是第m次迭代中获得的km形成的模糊算子，并且在估计x时其值固定的；Xm+1是第(m+1)次迭代中获得的xm+1形成的卷积算子，并且在估计k时其值是固定的。借助AMI，多变量最小化问题(3)被简化为单变量最小化问题(5)和(6)。为了解决这些问题，SAM使用VB等效地将它们转换为

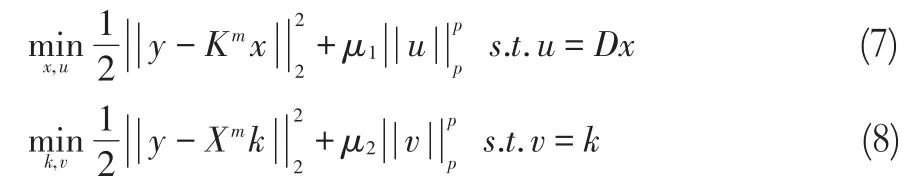
其中，u和v是松弛变量。通过引入这两个变量，问题(5)和(6)的数据拟合项和正则项被解耦，这简化了问题处理。再次应用AMI，问题(7)和(8)被分解为

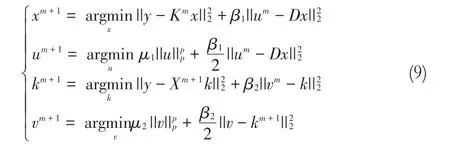
其中，参数β1和β2是正的常数。

该x子问题和k子问题是最小二乘类型的，可以使用快速傅里叶变换做如下计算

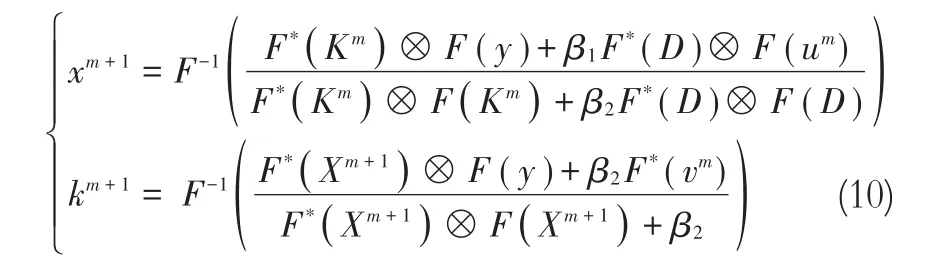
其中，F(·)和F-1(·)分别表示快速傅里叶变换和快速傅里叶逆变换；F★(·)是F(·)的复共轭；符号“⊗”表示点乘。对于u和v子问题，采用GST[18]计算可得

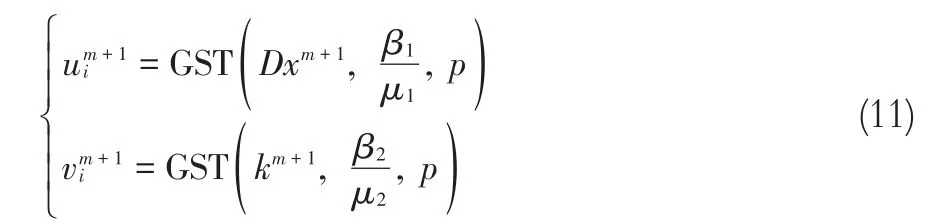
其中，um+1i和vm+1i分别是um+1和vm+1的任意元素。上述GST函数定义为综上所述，本文所提出的BID方法可以概括为：

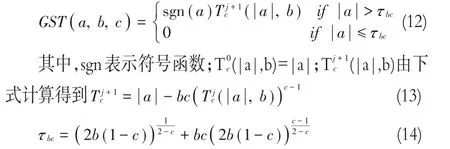
SPR-BID方法输入：模糊图像y和冗余变换D输入：μ1,μ2,β1和β2初始化：k0=u0=v0=0输出：xm+1和km+1 1．Form=0 to M do 2．根据式(10)更新xm+1 3．Loop执行多尺度策略{4．根据式(10)更新km+1 5．对km+1施加约束ki≥ 0和∑iki=1}6．Endfor

三、实验与结果

对图1所示合成模糊图像和真实模糊图像进行去模糊实验，以分析上述SPR-BID的性能。为了公平和准确，模糊图像从基准数据集[19,20]下载，这些数据集目前被大多数BID研究采用。SPR-BID和另一项研究中提出的方法[12]进行比较，比较从输出质量和平均速度两方面进行。对于去模糊后的合成图像，通过峰值信噪比（PSNR）客观地测量输出质量并对其视觉评估，去模糊后的真实图像仅通过视觉效果来评估，因为相应的原始清晰图像不存在。在所有实验中，文献[12]中的方法保留了其默认设置，以展示该方法的实际性能。经调整，SPR-BID方法参数设置如下：μ1=0.01，μ2=15，β1=1，β2=15000，p=0.5，M=10。为精确表征图像的全局特征和局部细节，采用双树复数小波变换作为冗余变换D。在配置 Windows7OS（64位），MATLAB R2012a平台，Intel Corei5-4258UCPU和4GBDDR内存的笔记本电脑上运行两种BID方法。每种方法执行5次去模糊任务，平均时间耗费见表1。

如图2以和表1所示，结果清楚表明所提出的SPR-BID方法在模糊估计和恢复清晰图像方面的有效性。与文献[12]中的方法相比，SPR-BID方法在速度和恢复质量方面具有优势。在视觉上，因SPR-BID方法复原了更多的细节特征（例如，突出边缘）并移除了更多的环形伪像，因此生成的去模糊图像更清晰。在速度方面，本文提出的SPR-BID方法可以在80秒内处理尺寸为1024×768的图像。

表1 两种方法处理图1时消耗的平均时间

图1 合成模糊图像和真实模糊图像

图2 BID方法的输出结果

四、结语

本研究致力于快速准确的图像盲去模糊，提出了一种稀疏先验正则化方法，它融合了lp范数正则化，SAM和GST。在交替迭代中，通过使用适当的方法计算和处理几个子问题，等效地解决了本文所创建的图像盲去模糊模型。在实验中，通过处理合成模糊图像和真实模糊图像，所提出的SPRBID方法被验证是有效的，通过对比实验还证实了SPRBID方法的优越性。