基于排队论的校园充电基础设施定量方法*

2019-01-22周智文马健霄韩正大汪子恒

物流工程与管理 2019年1期

□ 周智文，马健霄，韩正大，汪子恒

(南京林业大学汽车与交通工程学院，江苏南京 210037)

近年来，环境污染的加剧和电池技术的发展推动着电动汽车行业的不断进步。充电基础设施作为电动汽车行业的重要一环，其规划理论与方法一直是近年来的研究热点问题之一。电动汽车充电基础设施由于兼具停车与充换电双重功能属性，不能仅仅依赖传统的停车规划方法。而校园不同于一般商业用地和居住用地，其独特的多重用地性质也需要规划理论人员进行深入研究与探讨。

本文从电动汽车的停车需求即电动汽车的渗透率出发，进而考虑电动汽车的充电需求，以此建立双层模型进行充电设施的预测及规划。上层模型为校园电动汽车的停车需求预测，下层模型为基于排队论的充电设施计算模型。

1 校园电动汽车停车需求预测

1.1 电动汽车渗透率预测

电动汽车的渗透率即电动汽车数量占汽车总量的比例。校园电动汽车渗透率的预测受到以下几种因素的影响。

1.1.1 政策影响

公安部统计数据显示，截至2017年底，全国汽车保有量2.17亿辆，其中电动汽车保有量达153万辆，占汽车总量的0.7%。预计到2020年，全国汽车的总保有量预计将达2.8亿辆，其中电动汽车的保有量将超过500万辆，约占1.79%。

1.1.2 教职工群体的特殊性

校园作为一个特殊环境，其教职工群体普遍受教育程度较高，对电动汽车的可接受程度也普遍较高。笔者通过调查问卷统计得到，约占2%的教职工已购买电动汽车，约占21%的教职工有意愿购买电动汽车。

此外，教职工的远距离出行需求较少，日常通勤需求较大，如图1所示，约83%的教职工日常出行距离在20km以内，恰恰符合电动汽车的主要市场定位。

1.1.3 工作单位提供充电服务的影响

目前电动汽车产业发展最大的局限性在于汽车充电的不便，无法保证充电的方便快捷是目前广大车主选购电动汽车时主要顾虑的问题之一。而工作单位提供充电服务将会对该单位电动汽车渗透率产生较大影响。调查问卷统计约64%的职工将单位是否提供充电设施作为购买电动汽车的重要考虑因素。

图1 教职工日常通勤出行距离统计

1.2 电动汽车停车需求预测

校园电动汽车停车需求预测公式如下：

N电=N汽×α

(式1)

式中：N电为校园电动汽车停车需求(辆)；N汽为校园机动车停车需求(辆)；α为校园电动汽车渗透率。

2 校园电动汽车停车充电基本属性分析

电动汽车的充电行为具有较大的随机性和灵活性。

经调查分析发现，由于车辆形式的多样性和电动汽车运行条件等不确定因素的影响，到达充电站的电动汽车数量随时间变化的规律一般服从参数为λ的泊松分布。由于校园日间充电设施主要服务于教职工，而外来办事人员停留校园时间较短，充电需求较小，夜间主要服务于校园生活区居民。因此日间与夜间电动汽车到达率不同，需要分别考虑。

但是由于校园内教学工作区与生活区一般距离较近，甚至有部分重合区域。故充电设施合理布设在工作区与生活区相连处，令目的地处于可接受步行范围内，即可有效兼顾日间与夜间充电需求，减少充电设施的闲置与浪费。

此外，某一电动汽车到达充电站时，如果充电设施有空闲，则可以接受充电服务，当服务结束后就驶离充电站；如果充电设施没有空闲，则电动汽车需要排队等候服务，直到充电站有空闲的充电设施时再按照一定的秩序接受充电服务。

因此，从排队系统服务规则的角度来说，它属于先到先服务。电动汽车接受充电服务的时间服从参数为μ的负指数分布。所以校园电动汽车充电排队系统的随机过程具有马尔科夫性质，为一个生灭过程。

3 电动汽车充电设施的排队模型建立

由于校园该模型参数有三个，即电动汽车到达率λ，充电基础设施服务率μ，充电设施数量s。其平衡方程如下：

(式2)

由上式递推可得电动汽车接受充电服务的概率如下：

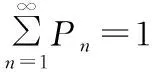
(式3)

该模型的主要特征可由特征指标体现。该模型特征指标如下：

(式4)

(式5)

(式6)

(式7)

系统中的平均车辆数：Ls=Lq+ρ

(式8)

(式9)

(式10)

充电设施排队系统单位时间的最优费用效益模型可以分为日间费用模型与夜间费用模型，其中各费用模型包括充电设施服务费用和电动汽车排队等待费两部分，并将两部分费用模型进行归一化处理，得到其最优效益模型如下：

F日=C1×s+C日×Ls日

(式11)

F夜=C1×s+C夜×Ls夜

(式12)

F=ω日×F日+ω夜×F夜

(式13)

式中：s为最优充电设施数量(个)；F为排队系统单位时间总费用(元)；F日为日间排队系统单位时间总费用(元)；F夜为夜间排队系统单位时间总费用(元)；ω日为日间排队系统单位时间总费用归一化系数；ω夜为夜间排队系统单位时间总费用归一化系数；C1为单位时间内单个充电设施的服务费用系数；C日为日间单位时间内单辆电动汽车的排队时间成本系数；C夜为夜间单位时间内单辆电动汽车的排队时间成本系数；Ls日为日间排队系统中的平均车辆数(辆)；Ls夜为夜间排队系统中的平均车辆数(辆)。

充电设施服务费用包括设施建设费用、运营维护费及充电电费等。其中，充电设施建设费用不仅包括充电桩及配套电线，还包括电网增容费用。

电动汽车排队费用主要为排队时间成本。由于日间(6点至18点)校园充电设施主要面向教职工服务，夜间(18点至次日6点)主要面向生活区居民服务，所以电动汽车排队费用以教职工和居民的时间成本为研究对象。

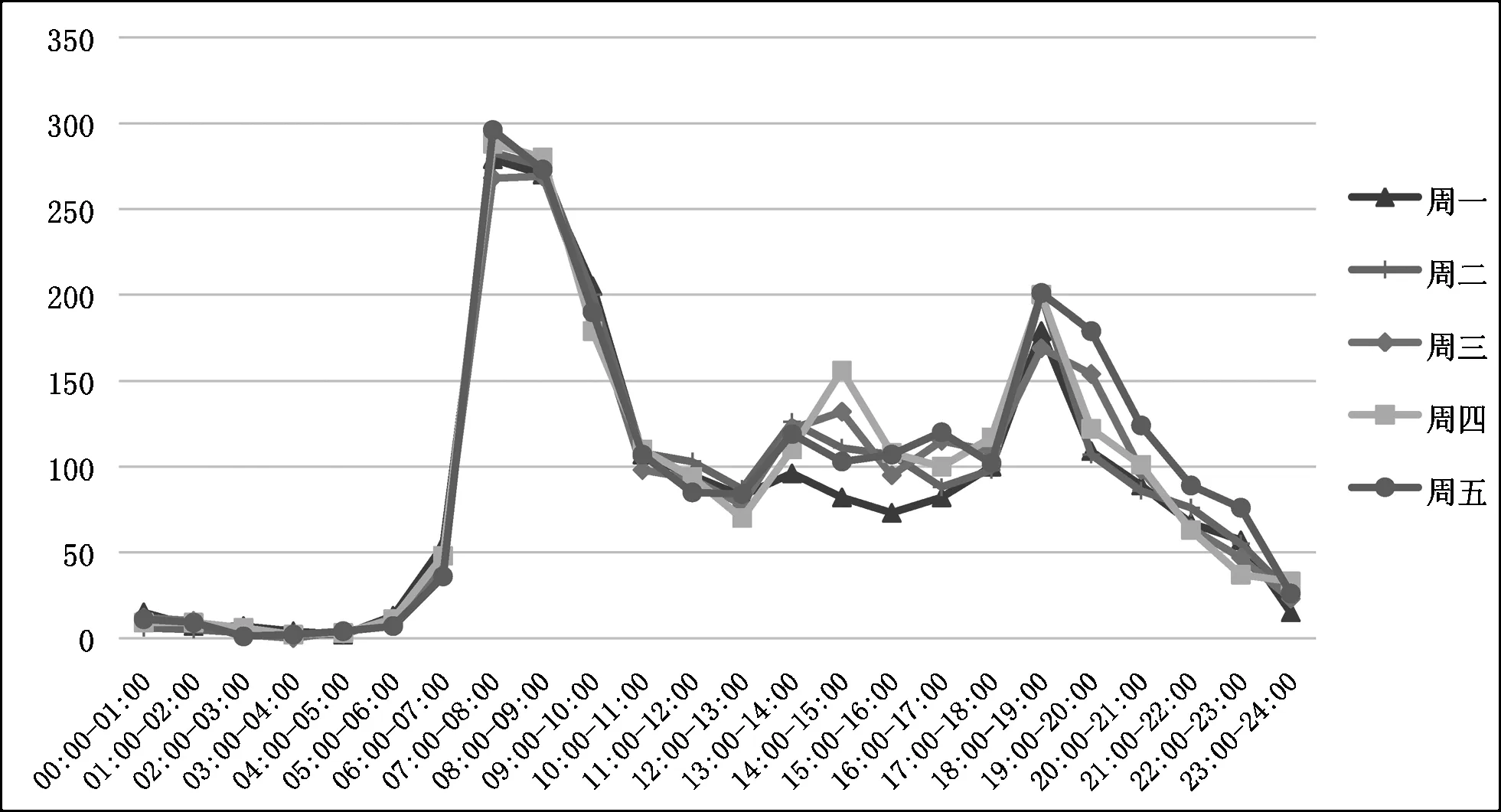
由于充电设施数量是一个整数解，所以最优充电设施数量s无法利用排队系统总费用对s的微分法求得，只能使用边际分析法求解。通过对模型输入不同的s值，令Fs

4 算例分析

本文以南京林业大学校园为例，进行校园电动汽车充电基础设施预测及规划。

4.1 电动汽车停车需求预测

南京林业大学地处南京市新庄地区，校园内停车需求主要集中在教学工作区与生活区，应分别进行停车需求预测。

目前该校在职教职工人数为2050余人，根据校园车辆管理系统数据已登记教职工车辆数为516辆。

该校生活区户数经调查如下表所示。根据《南京市建筑物配建停车设施设置标准与准则》，户型面积小于90m2的，机动车位设置标准为0.8车位/户；户型面积为90～144m2的，机动车位设置标准为1.0车位/户。则学校生活区的停车需求为1238辆。

表1 生活区住宅信息统计

综上所述，考虑到南京机动车保有量2015年、2016年、2017年同比增长率为7.1%、12%、7.5%。取机动车保有量增长率为7%，预测2020年南京林业大学教职工机动车停车需求为632辆，生活区机动车停车需求为1516辆。但是由于生活区部分居民为在职教职工，通过问卷调查可知这一比例约占62%。故对此部分停车需求进行折减，取折减系数为62%，即生活区停车需求为910辆。

综合考虑校园电动汽车渗透率相关影响因素，取南京林业大学教职工电动汽车渗透率为7%，生活区电动汽车渗透率α夜为5%，根据式1预测2020年南京林业大学教职工电动汽车保有量为44辆，生活区电动汽车保有量为45辆。

4.2 模型费用参数

4.2.1 充电桩建设及运营维护费用

参考行业平均价格标准，取每个充电桩运营维护费取0.45元/小时，充电设施平均建设费用为2.5万元/个。以7年使用寿命，残值率5%，使用率40%计算，折旧考虑后取充电设施平均建设费用为3.26元/小时。

4.2.2 充电电费

我国校园充电设施用电执行“一般工商业及其他”类用电价格。参考国家电网定价，1-20千伏的一般工商业及其他用电电价为0.8216元/千瓦时。充电桩额定功率取市场最常见的15kw，故取单个充电桩充电电费为12.32元/小时。

4.2.3 排队时间成本

时间成本，就是花费同样时间可能获得的工资收入，即车主从事其他工作单位时间内的工资与等待汽车充电过程中所花费时间之积。经抽样调查，南京林业大学教职工平均月薪8640元，每月平均工作约165小时，生活区居民平均月薪为7580元，每月平均工作约186小时。故取日间排队时间成本为52.36元/小时，夜间排队时间成本为40.75元/小时。

4.2.4 电动汽车到达率

考虑到最不利情况，即早晚高峰时段，取该时段电动汽车到达概率分布情况为参考。通过校园机动车辆进出管理系统数据统计得出，工作日07:00～09:00到达校园的机动车数量约占日间到达校园机动车总数的42.5%，且该时段机动车到达近似服从泊松分布，工作日18:00～20:00到达校园的机动车数量约占夜间到达校园机动车总数的62.6%，该时段机动车到达同样近似服从泊松分布。根据预测2020年南京林业大学教职工电动汽车保有量为44辆，生活区电动汽车保有量为45辆，即07:00～09:00电动汽车到达率为9.9辆/小时，18:00～20:00到达率为14.1辆/小时。考虑到电动汽车平均充电一次可使用2.2天，即充电概率约为45%，日间有充电需求的电动汽车到达率为4.5辆/小时，夜间有充电需求的电动汽车到达率为6.4辆/小时。