长时间小过载情况下固体火箭发动机两相流流场数值模拟①

那旭东，夏智勋，马立坤，颜小婷

(国防科技大学 空天科学学院，长沙 410073)

0 引言

近年来，随着反导拦截能力需求的不断提升，对高机动性能导弹发动机在过载情况下的可靠性和安全性均提出了更高要求。该类导弹的动力系统基本上采用高机动性能的固体火箭发动机，如美国的PAC-3、俄罗斯S-300V等，其主要技术特点是导弹在高机动运动过程中，要承受长时间小过载、中时间中过载、短时间大过载等过载情况[1-2]。高机动性能的固体火箭发动机大多采用含铝复合固体推进剂[3-4]，其燃烧产物中含有大量凝相颗粒Al2O3，发动机内流场是典型的气固两相流场。在过载条件下，高速凝相颗粒运动会引起燃烧室和喷管的局部聚集和冲刷，使局部烧蚀加剧，对发动机热防护结构产生很大影响。严重时会造成内绝热防护失效、壳体烧穿，从而导致飞行失败[5]。因此，研究和掌握过载条件下发动机内流场颗粒流的运动规律，对提升高机动性能固体火箭发动机的安全性及可靠性都具有重要的实现意义。

关于过载情况下固体火箭发动机内流场的两相流流动，国内外都进行了相关研究[6-18]，但对长时间小过载情况下发动机燃烧室及喷管的三维二相流流动的研究报道则较少[19-20]。本文以某飞行试验失败发动机为研究对象，针对其长时间小过载的工作特点，对燃烧室及潜入式喷管进行三维两相流流场的数值计算，在计算过程中，考虑了发动机旋转所带来的科氏加速度的影响。通过仿真计算分析了发动机内部两相流流场，并给出颗粒沉积区域及对应的颗粒冲刷角度、冲刷速度、颗粒粒径及浓度分布，旨在研究在长时间小过载条件下发动机内部颗粒的流动及沉积情况，为该类发动机后续的热防护设计提供指导依据。

1 计算模型和方法

1.1 发动机构型及网格划分

以某飞行试验固体火箭发动机为研究对象，该发动机采用翼柱形装药。对该发动机工作过程中3个典型时刻t1、t2和t3进行定常计算。其中，t1时刻为法向过载最大时刻；t2时刻为法向过载变小的拐点；t3时刻为装药完全烧完时刻。t1～t3典型时刻发动机几何构形如图1所示，主要包括前后封头、药柱、发动机壳体以及潜入式喷管。

采用六面体结构网格对发动机进行网格划分，并对壁面处及预估颗粒沉积量大的地方进行网格加密。图2给出了t1时刻其网格划分结果，其中上面为采用结构网格划分的块拓扑结构，下面为对应的发动机三维结构网格。

图1 发动机几何模型

1.2 数值方法及相关参数

采用Fluent软件开展仿真计算，两相流流动使用离散相模型DPM(Discrete Phase Model)求解。燃气作为连续相在欧拉坐标系下求解，颗粒相作为离散相进行处理，对每个颗粒在拉格朗日坐标下进行跟踪。燃气的控制方程采用N-S方程，颗粒相的运动轨迹则由拉格朗日方程确定[17]。

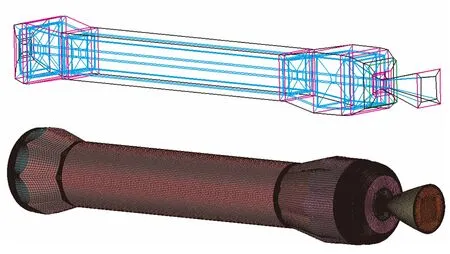
图2 t1时刻发动机块拓扑结构及网格划分

鉴于本文主要研究发动机中气相及颗粒相在长时间小过载条件下的流动特性，针对过载条件下发动机流动的特点，将复杂的两相流流动模型进行适当简化[21]：

(1)不考虑燃面退移过程，对选定的时刻进行定常计算；

(2)不考虑化学反应，将发动机内复杂的多组分气体简化为单一燃气，典型时刻的相关燃气参数见表1；

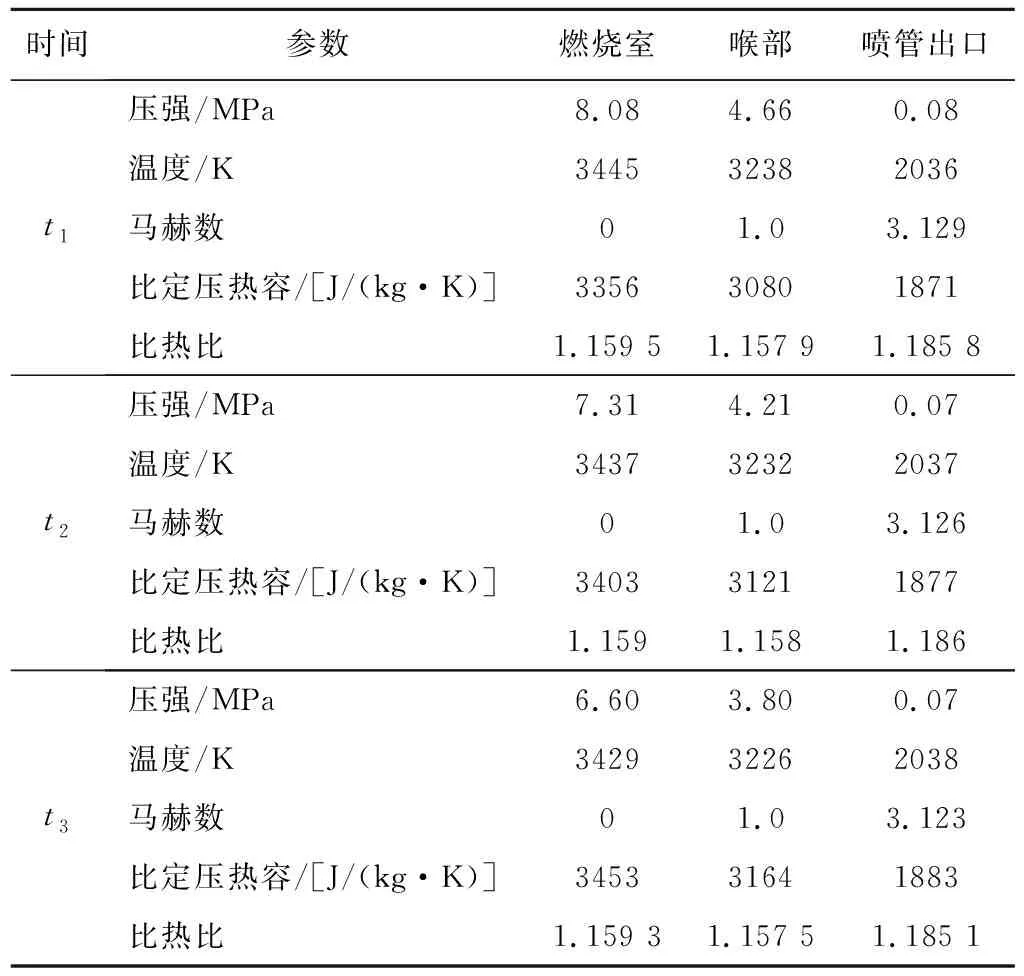
表1 发动机燃气参数

(3)燃气控制方程采用三维可压粘性N-S方程，采用标准k-ε湍流模型；

(4)固相颗粒为球形Al2O3，不考虑颗粒相的燃烧、蒸发、破碎过程以及颗粒间撞作用，忽略颗粒相变及密度变化的影响；

(5)忽略过载对气相的影响，对固相的作用通过UDF施加体积力给出。

颗粒直径分布采用Rosin-Rammler分布[18]，即假定颗粒直径d与大于直径的颗粒质量分数Yd之间有如下指数关系：

(1)

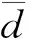
结合发动机所采用推进剂配方和文献[20, 22-23]，选取粒度分布范围为10～100 μm，颗粒直径分布指数为3.5，粒径平均直径为55 μm，颗粒的直径分布曲线如图3所示。

由于燃烧温度(见表1)明显高于Al2O3熔点温度2318 K ，所以固相颗粒的参数按液相Al2O3物性参数给定[24-27]，其中密度为2700 kg/m3、比定压热容1883 J/(kg·K)、热导率7.4 W/(m·K)。

颗粒壁面碰撞模型对模拟固体火箭发动机壳体内颗粒的沉积分布至关重要。Mundo等[28-29]基于大量实验认为，液滴撞击到壁面后的状态主要由液滴的动能决定，并提出了以Sommerfeld数K=We0.5·Re0.25的大小为判定准则，当K≤57.7时，液滴粘附于绝热材料壁面；反之，液滴在绝热材料表面发生反弹飞溅，其中We与Re分别为入射液滴的韦伯数与雷诺数[30-31]。

本文采用以Sommerfeld数为判定准则的颗粒壁面碰撞模型，对固体火箭发动机内颗粒碰撞壁面后状态进行判定。

1.3 边界条件处理

计算过程中主要用到三类边界条件：加质面边界条件、固壁面边界条件及出口边界条件。

(1)加质面边界：根据发动机实际设计情况给出当前时刻推进剂表面的质量流量，其中凝相占总质量流量的30%。颗粒从加质壁面均匀加入，在推进剂表面上应用反弹模型，在前封头、后封头及喷管固壁面上通过Sommerfeld数判定颗粒在壁面处的行为，在喷管出口应用消匿模型。

(2)固壁面边界条件：采用无滑移条件，即认为壁面处流体速度与该处壁面速度相同，法向压力、温度梯度为0。

(3)出口边界条件：发动机喷管出口气流处于超声速状态，给定出口处背压。

1.4 计算策略及验证方法

计算过程中，为节约计算时间，首先进行燃气流场稳态计算，燃气流场稳定后再添加颗粒项进行两相流场计算。连续相每计算200次进行一次颗粒的计算，颗粒计算的迭代步数为2000步。计算结果与表1中喷管喉部及喷管出口的压强、温度、马赫数等参量进行对比，验证数值结果的可靠性，并对网格无关性进行验证。

2 弹体坐标系及颗粒受力分析

2.1 弹体坐标系

弹体坐标系见图4。

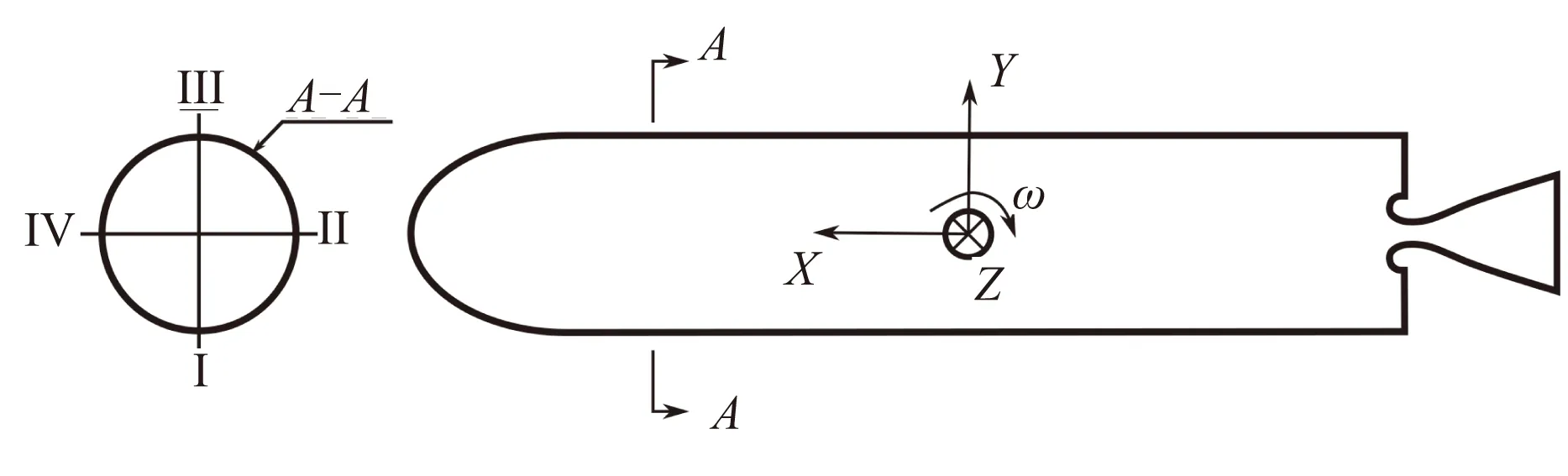
图4 弹体坐标系

图4 中，坐标系遵循右手定则，X轴为弹体轴向方向，指向弹头方向为正向，Y、Z轴垂直于X轴，Y轴位于Ⅲ轴上，Z轴位于Ⅳ轴上。轴向过载方向为X轴方向，法向过载方向为Y轴方向，横向过载方向为Z轴方向。

2.2 颗粒受力分析

在导弹飞行过程中，存在绕Z轴的角速度ω。当牵连运动为转动时，动点在某瞬时的绝对加速度等于该瞬时它的相对加速度、牵连加速度与科氏加速度的矢量和[32]。因此，发动机中的固体颗粒除了存在横向、轴向及法向的过载加速度外，还应考虑颗粒所受的科氏加速度。

颗粒的绝对加速度为

a绝=a相+a牵+a科

式中a绝为质点在惯性系中的加速度。

牵连加速度为

a牵=α×r+ω×(ω×r)

式中α为角加速度；r为颗粒位置矢量。

科氏加速度为

a科=2ω×v′

式中v′为颗粒相对于动坐标系的相对速度。

假定发动机3个方向的过载加速度分别为a轴、a法和a横，发动机绕Z轴的角速度为ω，忽略角加速度α，则有：

相对加速度为

a相=-(a轴+a法+a横)

牵相加速度为

a牵=ω×(ω×r)

科氏加速度为

a科=2ω×v′

将惯性坐标系设定在发动机上，在惯性坐标系中研究发动机中固相颗粒加速度，则固相颗粒所受的加速度为

a=a相+a牵+a科

=-a轴-a法-a横+

ω×(ω×r)+2ω×v′

可得绝对加速度在惯性直角坐标系下的3个分量分别为

ax= -a轴+[ωj(ωirj-ωjri)-ωk(ωirk-ωkri)]i+

ay= -a法+[ωi(ωirj-ωjri)-ωk(ωjrk-ωkrj)]j+

az= -a横+[ωi(ωirk-ωkri)-ωj(ωjrk-ωkrj)]k+

由于导弹只存在Z轴方向上的角速度，因此ωi=0，ωj=0，所以绝对加速度在发动机惯性直角坐标系下的3个分量最终表达式为

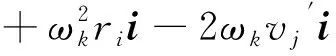
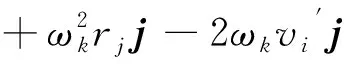
az=-a横

通过UDF的宏DEFINE_DPM_BODY_FORCE在计算中对颗粒施加过载加速度。所有变量单位采用国际单位制，角速度的单位为rad/s，加速度的单位为m/s2，速度的单位为m/s，颗粒位置矢量单位为m。t1～t3典型时刻的过载数值见表2。

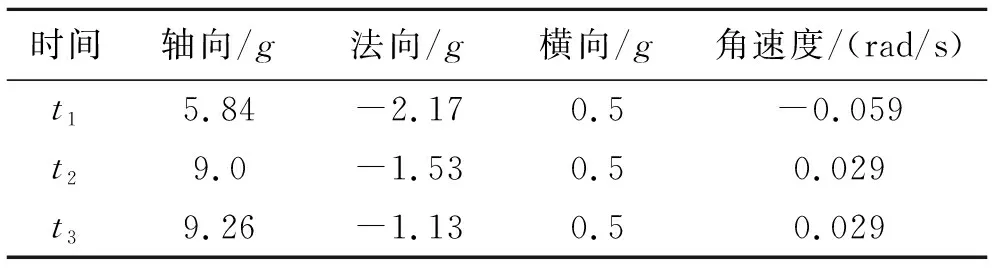
表2 过载数值

3 计算结果分析

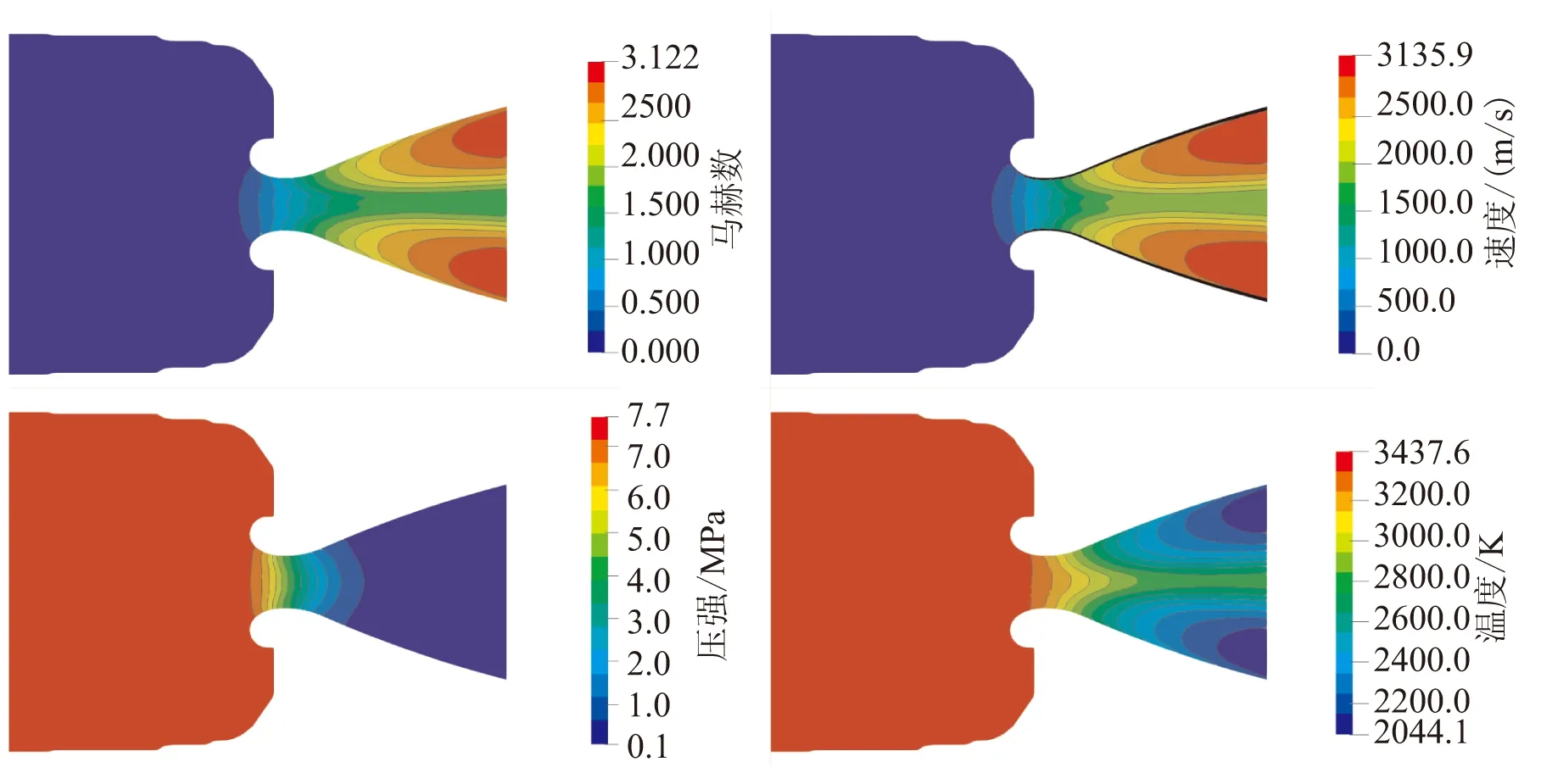
对该发动机在3个典型时刻下分别进行定常计算。图5分别为t1～t3时刻，Z=0平面处发动机内流场的马赫数、速度、压强及温度场计算结果。将图5中的数据与表1中喷管喉部及喷管出口的马赫数、压强和温度的数值对比，其结果基本一致。图5中，喷管二相流流场的速度和温度分布受颗粒的影响较大，而压力场受颗粒的影响较小。从速度场可看出，喷管轴心处的速度要小于接近壁面处的速度，而轴心处的温度要高于接近壁面处的温度，这是由于颗粒的滞后性造成的，是典型的气固颗粒流流场特征[33]。

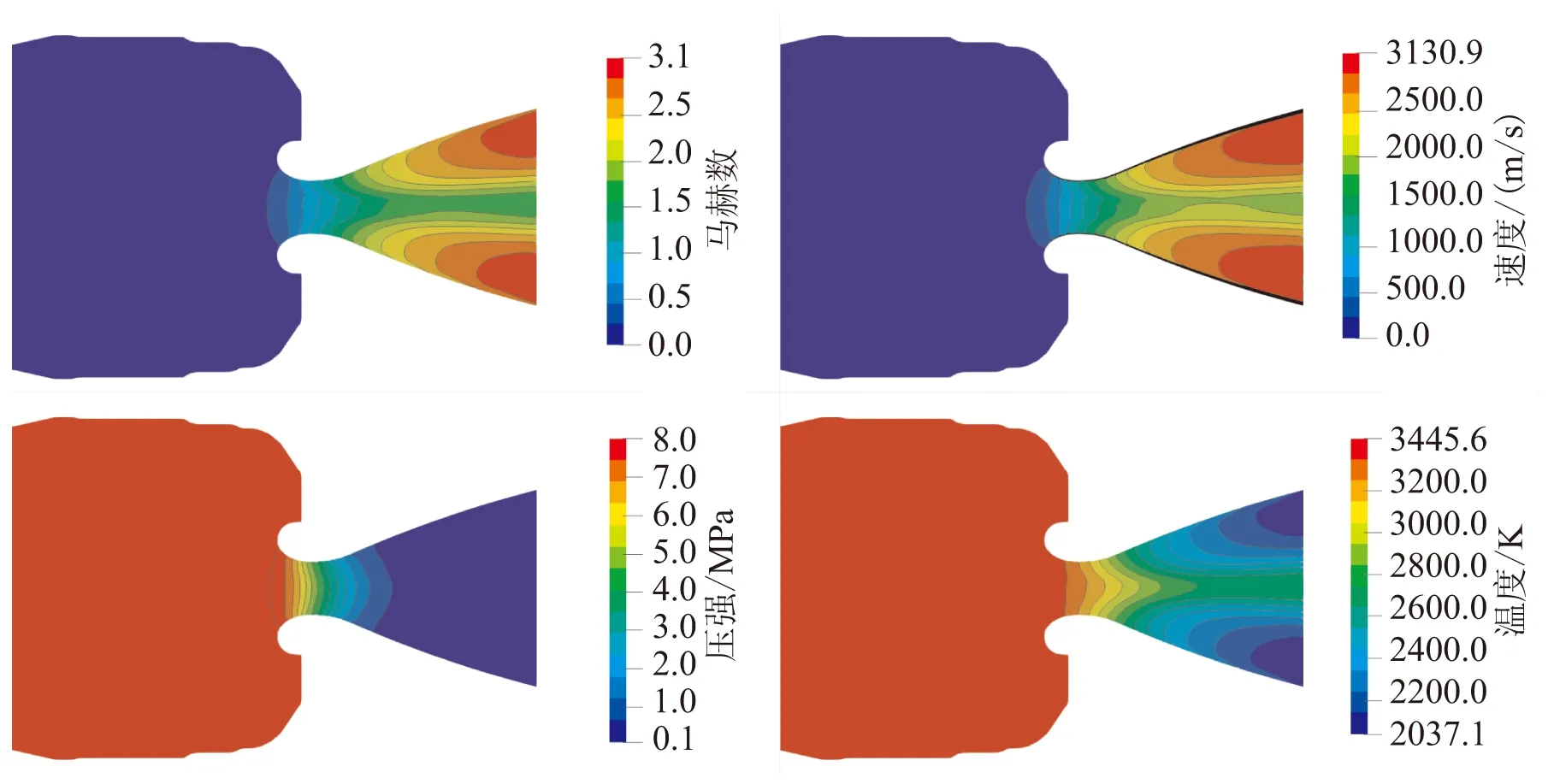
(a)t1时刻

(b)t2时刻

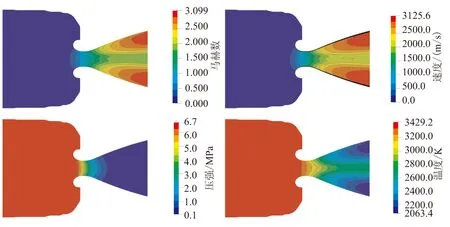
(c)t3时刻

图6给出了3个典型时刻的颗粒轨迹线分布情况。从图6可看出，颗粒从推进剂表面进入燃烧室后，在燃气气流的带动下迅速向发动机轴线方向靠近，与发动机壁面几乎不发生碰撞，而在离后封头及喷管较近的某些位置进入流场的颗粒比较容易撞击壁面，从而形成沉积。此外，从喷管处颗粒的轨迹可看出，大尺寸的颗粒基本沿喷管轴线附近区域流动，而小尺寸的颗粒远离喷管轴线区域流动。这主要是小尺寸颗粒的随流性较好，在气流带动作用下轨迹发生了偏转。

图7给出了t1时刻发动机颗粒沉积浓度分布情况。可看出，浓度分布较大的位置主要集中在后封头圆弧过渡段及潜入式喷管潜入段壁面处。

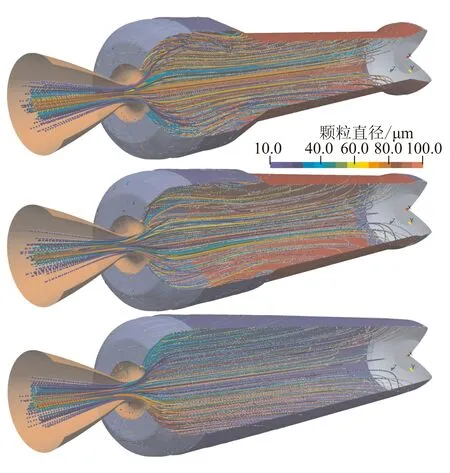
图6 颗粒轨迹线

图7 t1时刻颗粒沉积浓度分布

图8为t1、t2和t3时刻发动机后封头及喷管处颗粒沉积浓度分布放大图。其中，左图为从发动机外部视角观测颗粒沉积浓度分布；右图为从发动机内部视角观测后封头及潜入式喷管浓度分布。

从图8(a)可看出，后封头处的颗粒沉积浓度要大于喷管处，主要集中于后封头圆弧过渡段处，且在承载方向上沉积浓度发生偏转。从图8(b)可看出，t2时刻其后封头圆弧过渡段处颗粒沉积浓度分布没有发生明显的偏转，但其仍为颗粒沉积浓度分布最大处，在喷管潜入段及与其相邻的后封头平面处颗粒沉积浓度在承载方向上发生了偏转。从图8(c)可看出，t3时刻其颗粒沉积浓度在后封头圆弧过渡段处和喷管潜入段处在承载方向上发生了偏转，且颗粒沉积浓度最大处仍处于圆弧过渡段处。

针对t1时刻的工况，除了考虑所有过载情况下的计算，还进行了无过载计算及无横向过载计算。图9与图10分别为无过载及无横向过载条件下后封头及喷管处颗粒沉积浓度分布。分析对比图8(a)、图9和图10可知，对于后封头圆弧过渡段，当无过载时颗粒的沉积在周向方向上分布相对均匀，无明显聚集偏转，最大沉积量约为23 kg/m3；当有过载时沉积的分布发生了明显的偏转，在承载方向上沉积量有所增加，考虑所有过载情况下时的最大沉积量约为42.5 kg/m3，约为无过载情况下的1.89倍；无横向过载(0.5g)情况下的最大沉积量约为42.8 kg/m3，两者之间差距并不明显。

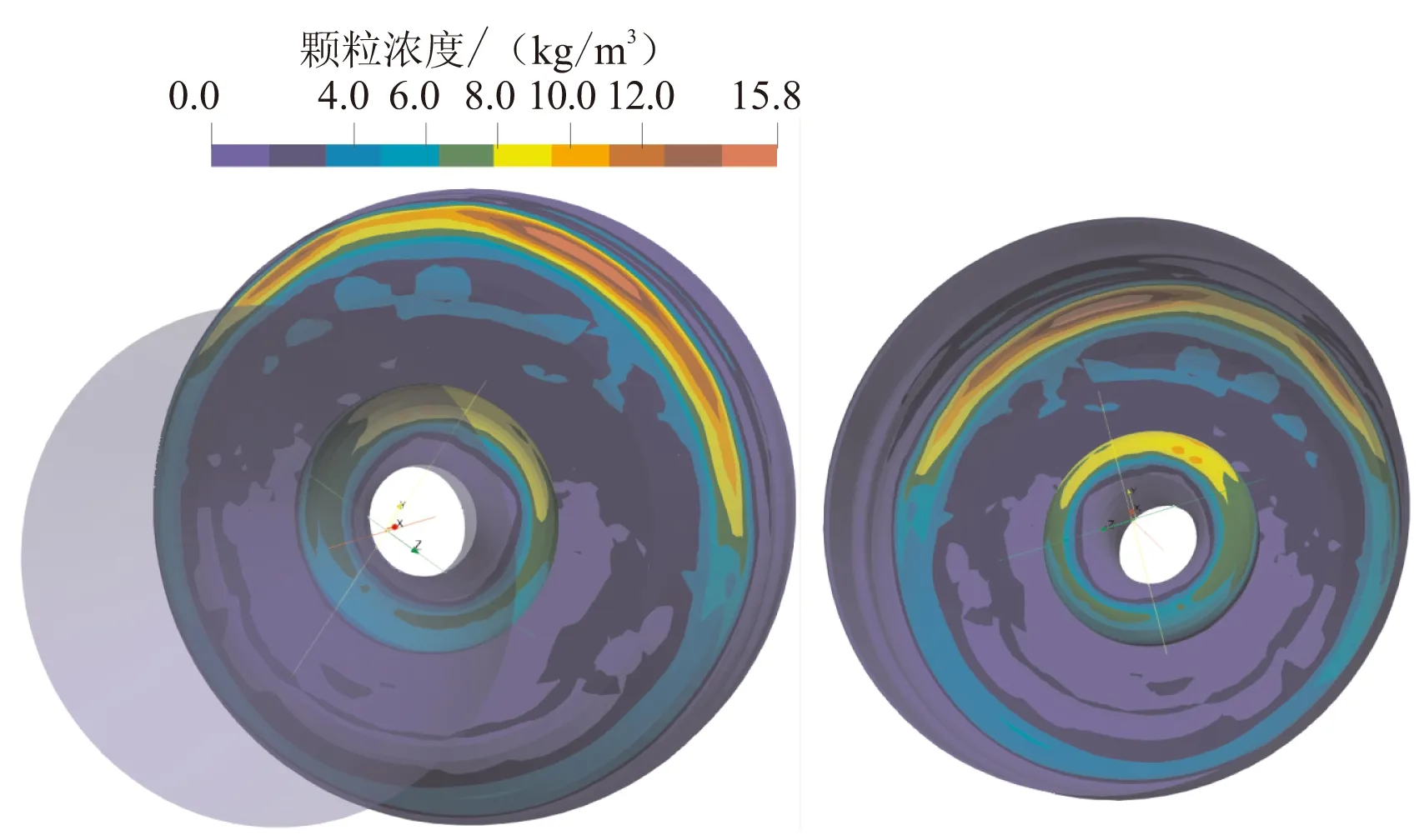
(c) t3时刻

由于颗粒的冲刷速度与冲刷角度对研究颗粒对绝热层的冲击烧蚀具有重要意义，因此对图8(b)、(c)及图9中后封头圆弧过渡段处颗粒的冲刷速度及角度进行统计，结果见图11和图12。从图12可看出，颗粒在后封头圆弧过渡段处的入射角度大多在20°～40°之间，属于切向的剪切冲蚀。

此外，还对后封头圆弧过渡段处颗粒尺寸进行了统计，如图13所示。可看出，后封头圆弧过渡段处沉积的颗粒主要为相对较大尺寸的颗粒。

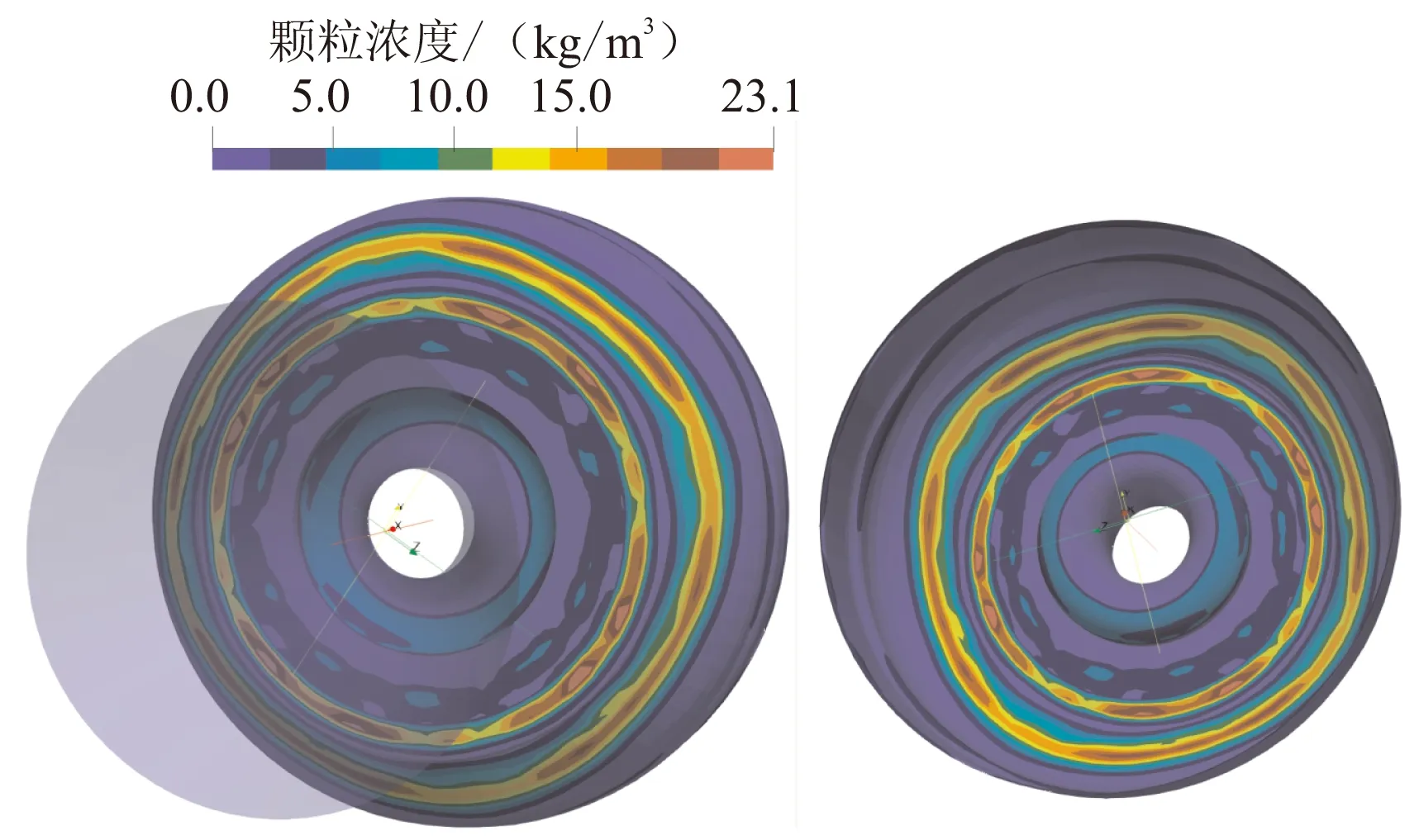
图9 t1时刻无过载条件下后封头及喷管颗粒沉积浓度分布

图10 t1时刻无横向过载条件下后封头及喷管颗粒沉积浓度分布

图11 后封头圆弧过渡段处颗粒的冲刷速度分布

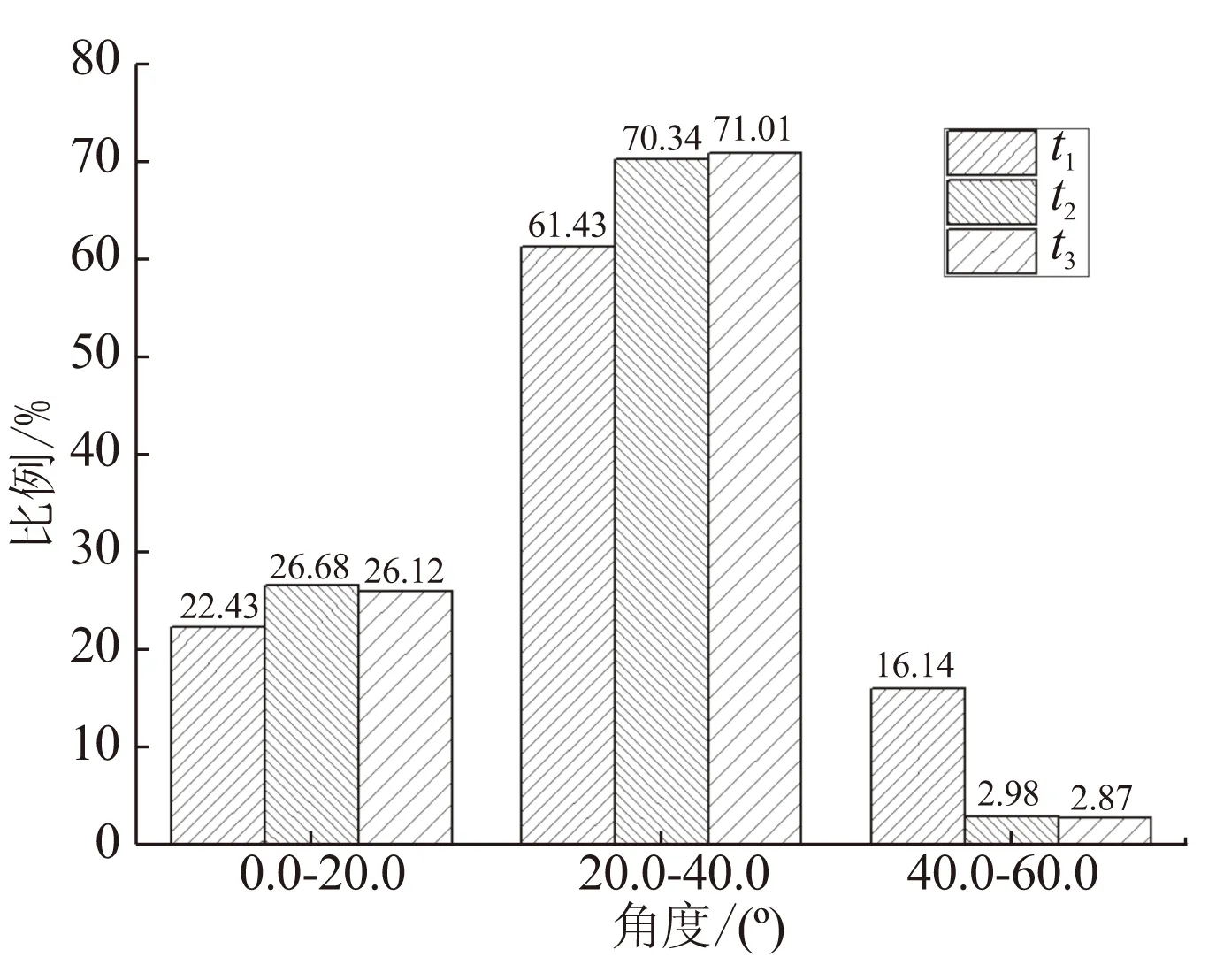
图12 后封头圆弧过渡段处颗粒的冲刷角度分布

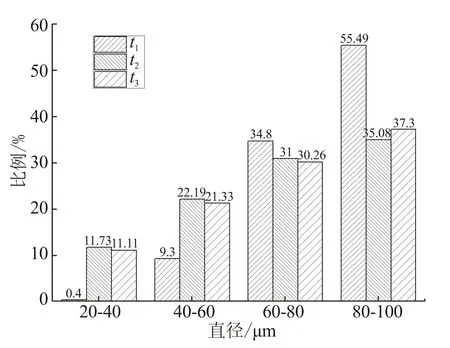
图13 后封头圆弧过渡段处颗粒的粒径分布

从以上仿真结果可知，在进行此类发动机绝热层设计时，要充分考虑发动机在长时间小过载情况下所带来的影响，对颗粒沉积量大的地方，要加大绝热层的厚度，以防将发动机壳体烧穿，造成发动机失效。

4 结论

(1)本文以某飞行失效固体火箭发动机为研究对象，针对其长时间小过载的工作特点对其三维两相流内流场进行数值模拟，在计算过程中考虑了发动机旋转所带来的科氏加速度的影响。分析了两相流流场特性，并给出了凝相颗粒沉积位置、沉积量及颗粒的冲刷速度、角度和粒径的统计分布。

(2)分析3个典型时刻下的颗粒沉积分布，指出沉积量大的位置主要集中在后封头圆弧过渡段处，且沉积的分布发生了的偏转，在承载方向上沉积量有所增加。针对t1时刻，分析对比无过载、无横向过载以及考虑所有过载的情况，相比无过载情况，考虑所有过载时，其最大沉积量为无过载情况下的1.89倍。

(3)在此类发动机后续设计过程中，要充分考虑长时间小过载情况下两相流流场对发动机带来的影响，在颗粒沉积量大的地方要进行充分的热防护。