大长径比固体火箭发动机工作过程中压力响应的数值研究*
2019-01-18李冬冬
王 革,张 莹,李冬冬,孙 娜
(1.哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001;2.上海航天动力技术研究所,上海 201109)
0 引言
由于工艺限制及发动机运输问题,大型固体火箭发动机多采用分段式装药,每段装药用绝热环来支撑。在发动机工作过程中,随着燃面推移,绝热环便成为主流中的障碍物,当主流流过绝热环时便会形成障碍涡脱落。涡脱落作为发动机内一种常见的现象,受到越来越多的国内外专家学者的研究。
Flandro和Jacobs[1]于1975年提出发动机内的涡脱落现象可能是燃烧不稳定[2]的另一源头,涡脱落会导致燃烧室内压力振荡。早期的实验和数值分析论证了潜入式喷管中流动和声场的耦合,并且证明声压等级随喷管空腔体积线性增加。Anthoine J等[3-4]用CPS模拟了流动和声学耦合现象,结果表明空腔的存在会导致更高的压力振荡。Stella F等[5]对SRM中产生的压力振荡展开了数值研究,证明了空腔对流动涡影响的重要性。认识声场结构异常重要,Jiang X[6]通过对亚声速轴对称射流内的声场算法进行了研究,发现轴对称Lilley方程的预测与声场的DNS结果之间存在很好的一致性。刘佩进等[7]对分段SRM中涡声耦合的实验研究现状进行了总结,并且通过研究发现头部空腔、段间空腔以及潜入式喷管处空腔的存在都会对压强振荡产生较大影响。王健儒等[8]通过LES模型对不同燃面下的准稳态内流场进行了模拟,发现在点火初期表面涡脱落占主导地位,随着燃面逐渐推移,障碍涡脱落占主导。杨尚荣等[9]从流动稳定性的角度进行数值模拟,并根据参考文献[10-12]的理论方法进行理论求解,二者对比结果表明加质表面会产生表面涡脱落;此外,苏万兴[13]对大长径比SRM中不稳定燃烧进行了线型预估,结果表明,随着燃面的退移,压力耦合响应增益与喷管阻尼均随之减小。张峤等[14]以VKI实验发动机作基础,通过LES方法揭示了SRM内的涡声耦合机理,结果表明二维轴对称大涡模拟方法基本满足发现涡声耦合规律的精度要求。李鹏飞[15]采用LES方法,通过改变障碍物的高度和位置、空腔大小和来流速度大小对固体火箭发动机中涡脱落现象展开研究,结果表明:障碍物越接近喷管,涡脱落频率越大;当来流速度不断增加时,涡脱落频率也越大;涡脱落频率与空腔体积成反比。Raheem[16]通过将燃烧室流动简化成二维瞬态不可压流动,借助Fluent软件对Shanbhogue[17]的实验进行模拟,李强等[18]又用大涡模拟方法针对Shanbhogue的部分实验工况展开数值模拟,通过和实验结果以及Raheem的计算结果进行对比发现:其计算结果与实验基本相符,究其原因是涡结构与声波有较强的三维性,通过二维模型很难模拟出其特点,并且LES能更准确地模拟涡脱落现象。张翔宇等[19]采用三维LES方法对固体火箭发动机C1x模型展开了数值模拟。杨羽卓[20]对带潜入式喷管的含一个障碍的Ariane5缩比模型发动机展开了研究,结果表明,压力场更能反映声场特点,速度场与涡量场更多表现出的是流动特点。其还对涡脱落撞击冷流缩比模型的喷管可能会导致的压力振荡展开了数值模拟[21]。
显然,国内外专家学者对发动机内的涡脱落现象是非常关注的,但是这方面的研究局限于冷流实验模型和准稳态内流场模拟。本文就大长径比固体火箭发动机内的障碍涡脱落现象展开了研究,重点分析了涡脱落过程中的压力响应规律,结合开发的含包覆层界面识别方法,模拟了两端包覆装药大长径比发动机燃面动态推移过程,并且从准稳态和燃面动态推移两个角度展开了对比。
1 物理模型和计算方法
1.1 物理模型
声学不稳定性会引起内弹道压力和推力振荡,导致火箭发动机性能降低,以Ariane5助推器为例,Ariane5固体火箭发动机中分段燃烧室由三段推进剂组成,并采用绝热环隔开,确保热防护。参考文献[3],在本文中只采用了一个绝热环,分析绝热环障碍对声场的影响。
参考冷流模型,基于含包覆层界面识别法,结合文献[3]中信息设计出装药,以绝热环暴露在主流中9 mm作为初始燃面,药柱两端被包覆,只有侧面燃烧。本文设计的含装药大长径比发动机几何模型如图1所示,阴影部分为药柱,其余为流场区域,图中尺寸单位为mm。其中,喷管喉部直径为26 mm,此发动机的膨胀比为6.05。在燃面推移的过程中燃面附近不断加质加热,从而模拟燃面推移过程中燃气的产生。
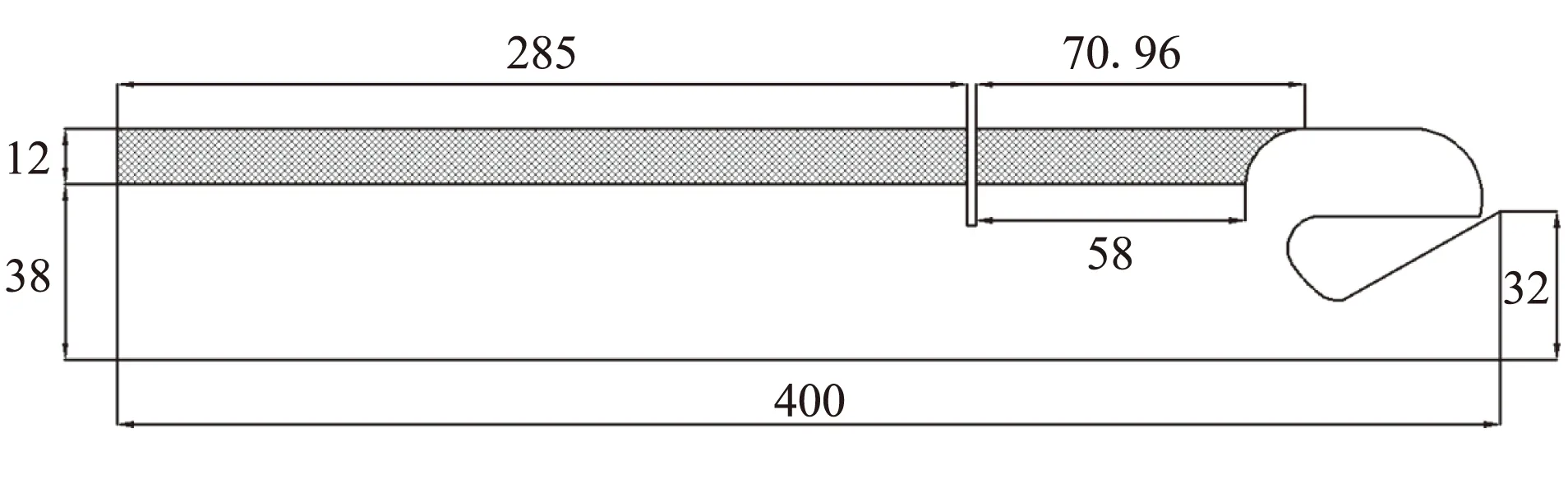
图1 燃面推移几何模型示意图
一般研究大长径比发动机内的涡脱落现象都采用准稳态计算,从而得出不同型面下的内流场变化。虽然本文可以采用改进的LSPM方法实现燃面动态推移下的发动机内工作过程数值模拟,但是进行准稳态内流场研究仍很有必要。对准稳态内流场的分析可以对燃面动态推移结果起到一定参考作用。为了解准稳态计算过程中的压力响应规律,本文对图1中装药推移到两个时刻燃面下的流场进行了准稳态计算,分别是初始燃面(型面A)和装药被燃去一半处燃面(型面B),对应的计算模型如图2所示。其中,型面A条件下绝热环高度为9 mm,型面B条件下绝热环高度为15 mm。
图1、图2中物理模型均采用结构网格,网格质量较高。为能够更加准确地捕捉流场,在近壁面和绝热环附近均进行加密,加密后的网格如图3所示。为能将准稳态计算结果与瞬态结果展开对比,均采用如表1所示的推进剂和燃气参数。
1.2 计算方法
本文采用大涡模拟方法进行数值模拟,此方法本质是大涡直接求解,小涡用模型。小涡对大涡的影响用近似的模型体现,这称为亚格子雷诺应力,文中采用WALE亚格子模型。大涡模拟的两个重要步骤分别为滤波和建模。滤波方程如式(1)所示。
文中基于多孔介质模型[22],结合Level-set方法实现燃面推移,通过添加质量、动量和能量源项模拟燃气的生成。其中Level-set方程见式(2),质量、动量和能量源项详见式(3)~式(5)。
方法的具体细节参考文献[22]。
后文中的计算涉及到装药两端包覆的情况,为此基于参考文献[22]的算法,开发了含包覆层复杂界面识别方法。
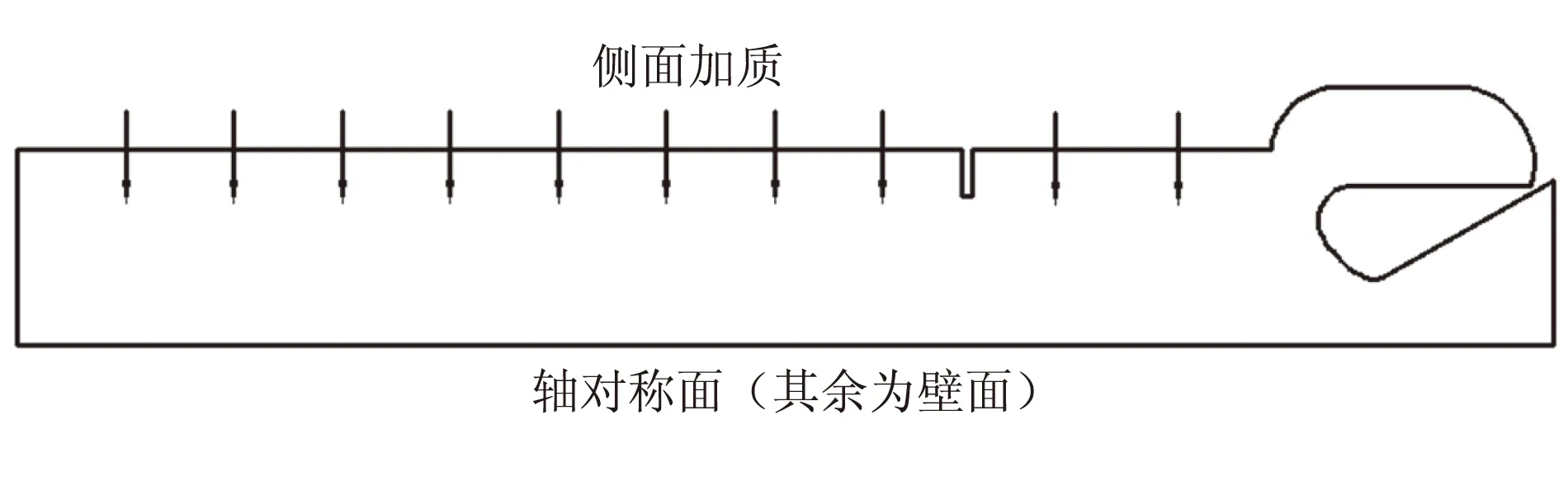
(a)型面A
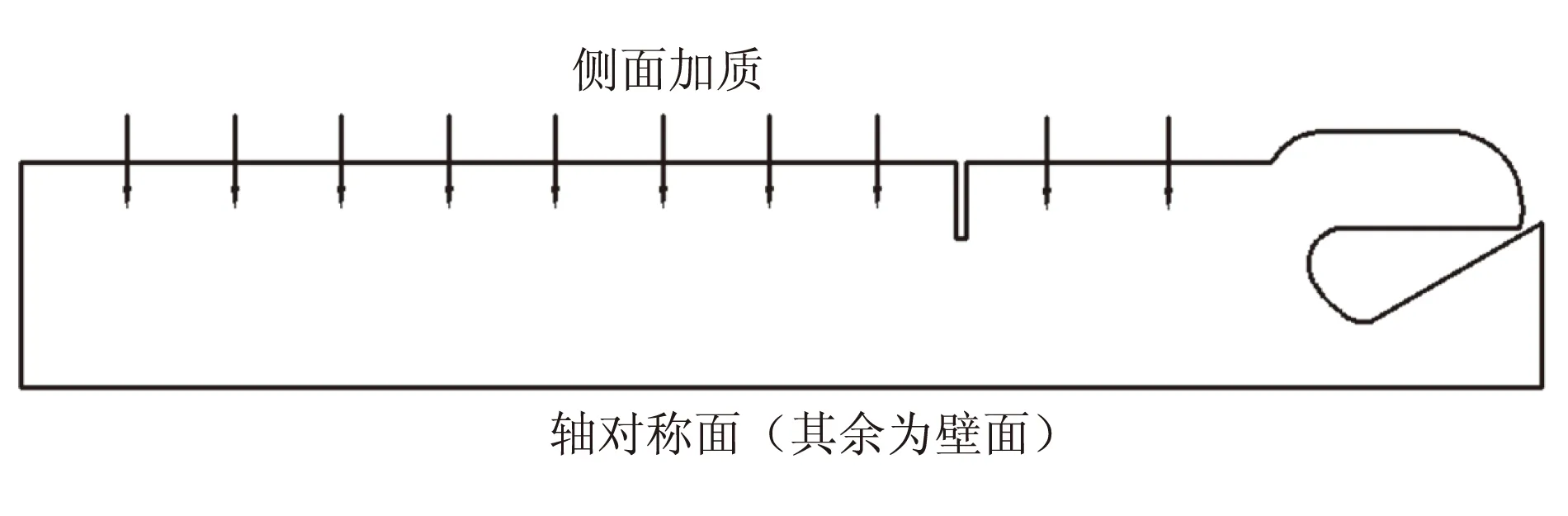
(b)型面B

图3 近壁面及障碍处网格加密

性能参数数值推进剂密度ρp/(kg/m3)1800燃速系数a0.006燃速指数n0.2比定压热容cp/[J/(kg·K)]1965.55相对分子量M30.303燃气总温T/K3532
注:对应的压强单位为MPa。
(1)

(2)
(3)
(4)
(5)

图4为复杂含包覆层的计算模型,只有侧面推移,即只有一条界面随时间推移,包覆层不沿着其中垂线向固体域内部推移,而是随着界面的推移而消失。图中固体域两侧为包覆层,在实际建模过程中包覆层厚度不体现,只是象征性的内部边界,将流体域分成如图所示无填充的4块方便说明。将图4中的1和2区域设为虚拟固体域,3是为了方便识别界面而划分的流体区域,这三个区域即为改进LSPM的计算域,其大小可以随意设定,但都是越小越好,能够极大的缩短初始化和界面更新时间。(虚拟)固体域和流体域相交的部分即识别成初始界面。很明显,界面不包括含包覆层的部分,但是却多出了两段界面,如图4中红色虚线所示。因此,燃面面积的计算方式需进行处理,处理的方式为只计算固体域和流体域3中识别到的界面。这种处理方式要求在网格划分时将计算域分成更多的子区域,但提高了算法的适用范围,并缩短了计算时间。
为避免中心差分格式引起的数值振荡,动量方程采用BCD格式进行离散;连续性方程和能量方程采用二阶迎风格式;为使速度与压力能更好地满足动量和连续性方程,采用PISO算法进行压力速度耦合求解。
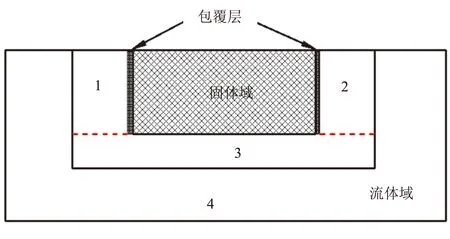
图4 含包覆层界面识别模型示意图
2 数值校验
国内外研究涡脱落现象通常以冷流实验为主,而本文旨在模拟实际发动机的工作过程中的涡脱落现象,发动机工作在高温燃气下,与冷流实验的285 K不同,因此对冷热流注入方式下的计算结果展开对比显得尤为重要。本节数值校验旨在研究流动温度可能带来的影响,为之后研究高温燃气下的流动过程作铺垫。
2.1 发动机固有频率
发动机能够近似看做两端封闭圆柱形腔体,声在其中的传播以一维纵向驻波为主,燃烧室内产生的涡在下游与喷管碰撞产生声波,波经过传播又在燃烧室头部被反射回来,此反射波与原先的瞬时波干涉产生驻波[21]。因此,发动机可近似看做一个共振器,其纵向固有频率计算公式如下:
f纵=nc/2L
(6)
式中f纵为纵向固有频率;n为模态阶数;c为当地声速;L为燃烧室长度。

当涡脱落频率与固有频率相近时,发动机内可能会发生涡声耦合现象,涡脱落频率会在各阶声频间跳跃,并且涡和喷管收敛段的碰撞又会将声压提高到共振条件,并将能量以一阶声模态反馈至边界层,把涡脱落频率调整到对应声频,导致压力振荡被放大。
2.2 冷热流注入结果分析
数值校验的计算模型与图2(a)一致,为冷流模型,参照文献[3]采用头部加质,以0.3 kg/s空气头部注入,而非图中的侧面加质。冷热流数值模拟除了空气温度不同,其他计算设置均一致。其中冷流温度为285 K,热流温度为3300 K。
对以冷、热流头部注入方式得出的内流场结果分别展开分析,计算过程中对头部压力进行监测,图5为冷热流注入方式下头部压力振荡曲线的FFT分析。从图5可看出,冷流注入方式下,各阶峰值及其对应的响应频率较热流注入条件下低很多。
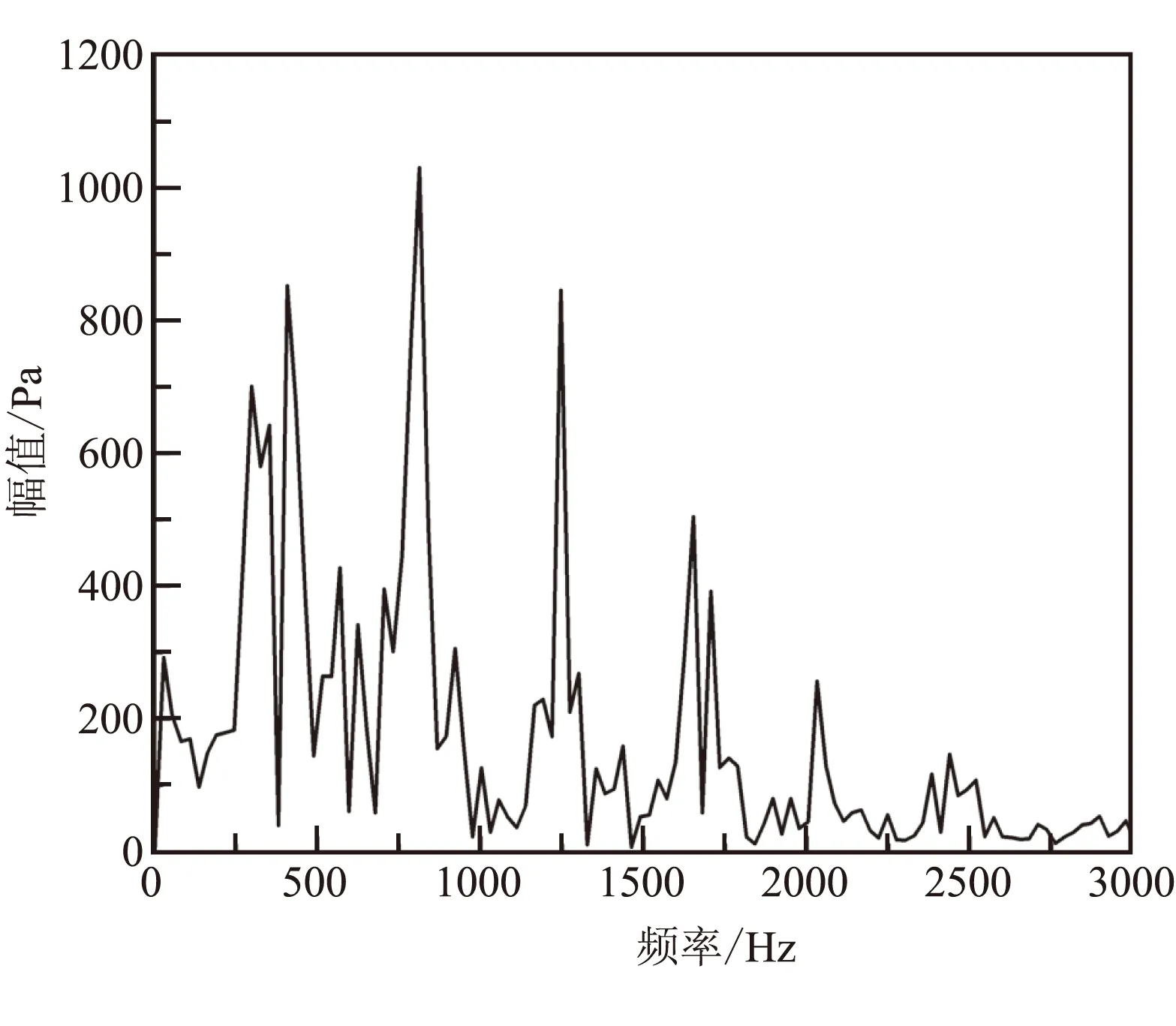
(a)冷流头部注入

(b)热流头部注入
从冷热流注入条件下的数值分析结果可看出:热流对应的压力振荡响应频率集中在高频,而冷流注入对应的压力振荡响应频率集中在中频。
冷热流对比旨在研究音速对压力波动响应频率的影响,式(6)中已经交代了音速对固有频率的影响,针对本节模型,分别计算出了冷热流固有一阶和二阶频率。表2为冷热流数值计算中各阶压力峰值对应的响应频率、冷流实验值及发动机固有频率的对比。从表2数据可看出:
(1)冷流数值模拟下压力振荡一阶和二阶峰值对应的频率分别为406、840 Hz,与冷流实验值基本吻合,认为数值计算结果可信。
(2)热流数值模拟与冷流数值模拟之间唯一的区别就在于温度,因此计算结果的不一致说明了温度会对压力响应频率产生较大影响。从热流数值模拟下压力振荡一阶和二阶响应频率分别为1447、2935 Hz,可以推测出压力响应频率与温度可能是开方倍关系,即压力响应频率与音速成正比。
(3)根据式(6)计算出的冷热流条件下的发动机固有频率,其大小与数值模拟结果比较接近,很容易产生涡声耦合。但是未发现涡声耦合现象,说明响应频率与发动机固有频率接近并不是产生涡声耦合的必要条件。

表2 头部压力振荡响应频率对比
3 大长径比SRM准稳态内流场研究
针对1.1节中设计的型面A和型面B两种物理模型,对大长径比固体火箭发动机中准稳态内流场展开了研究,方便与燃面动态推移过程中的瞬态内流场形成对比。
3.1 型面A条件下准稳态内流场模拟拟
采用图2(a)中计算模型,与燃面动态推移过程中加质方式一致,根据该型面下的燃面位置和大小进行侧面加质,实现了型面A条件下的准稳态内流场的数值模拟,通过对发动机头部及凹腔位置压力的监测,对该型面下的压力响应规律展开了分析。
分别对燃烧室头部和凹腔监测点压力作FFT分析,其结果如图6所示。从图6可看出,发动机头部监测点平均压力振荡幅值在1000 Pa,而凹腔监测点平均压力振荡幅值能达到2000 Pa。
从图6统计出监测点的前四阶峰值对应的频率见表3。从表3可见,虽然监测点所处发动机中的位置不一致,但是前四阶峰值对应的响应频率相同,在型面A条件下的前四阶压力响应频率分别为1100、2631、3970、5262 Hz。结合图6中峰值大小发现,虽然不同位置处的各阶响应频率一致,但其对应的峰值大小不一。凹腔处频谱分析的幅值更大。
3.2 型面B条件下准稳态内流场模拟
采用图2(b)中计算模型,与燃面动态推移过程中加质方式一致,根据该型面下的燃面位置和大小进行侧面加质,实现了型面B条件下的准稳态内流场的数值模拟,通过对发动机头部及凹腔位置压力的监测,对该型面下的压力响应规律进行了分析。
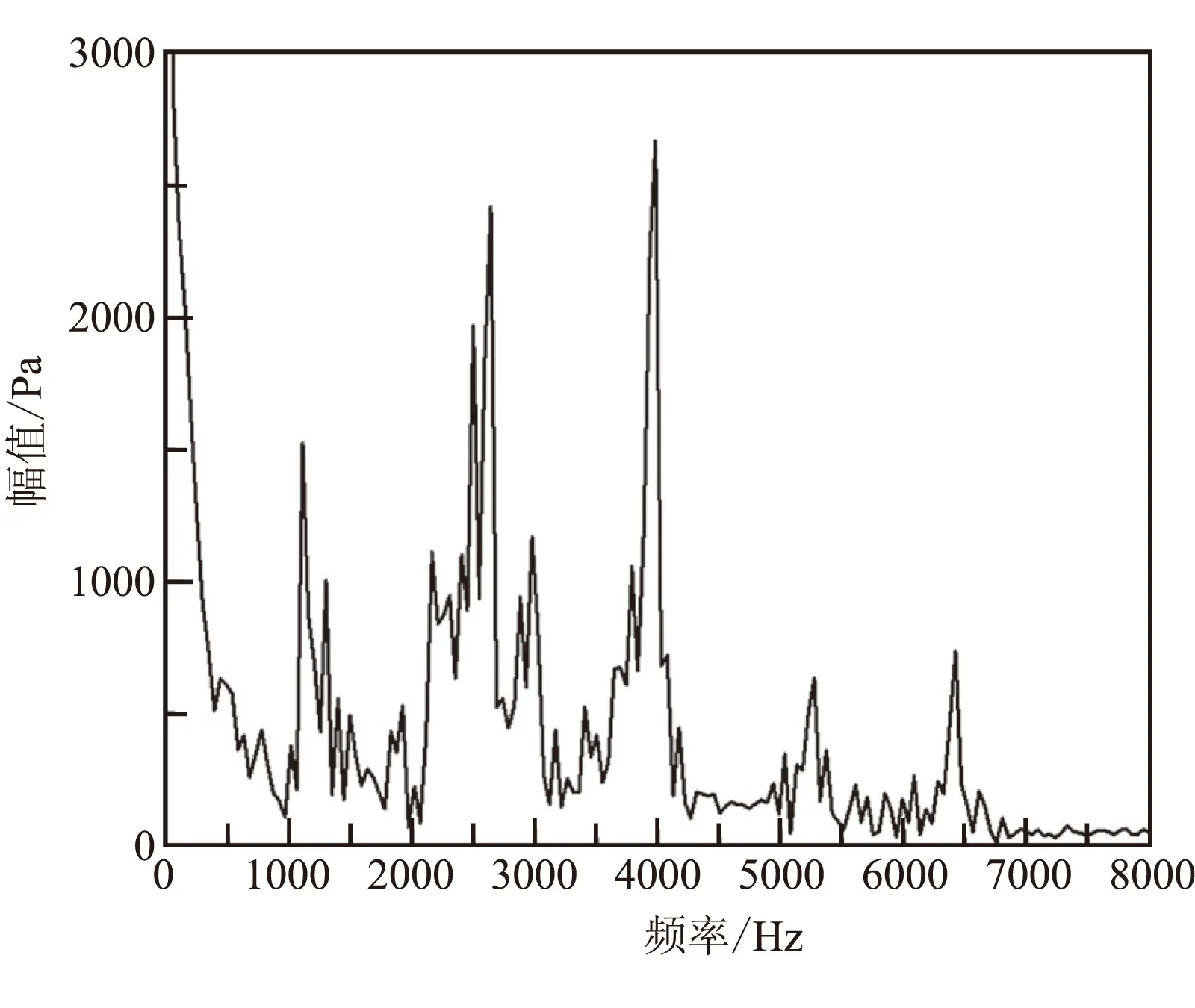
(a)发动机头部

(b)凹腔处

阶数头部凹腔处阶数头部凹腔处一阶11001100三阶39703970二阶26312631四阶52625262
分别对监测点压力做FFT分析,其结果见图7,表4为图中各阶峰值对应的响应频率统计结果。结合图7、表4中的信息可发现,发动机头部和凹腔处的压力频谱分析曲线规律一致。表4中信息也表明两个监测点前四阶响应频率也相同,其中前四阶峰值对应的各阶响应频率分别为1321、2541、3965、5337 Hz。与型面A条件下的准稳态计算结果相同,凹腔处压力振荡平均幅值大约为2000 Pa,而发动机头部压力平均振荡幅值只有1000 Pa,可见凹腔处的扰动较大,涡的运动也比较复杂。
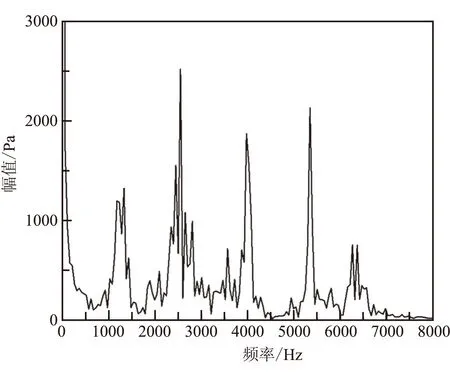
(a)发动机头部
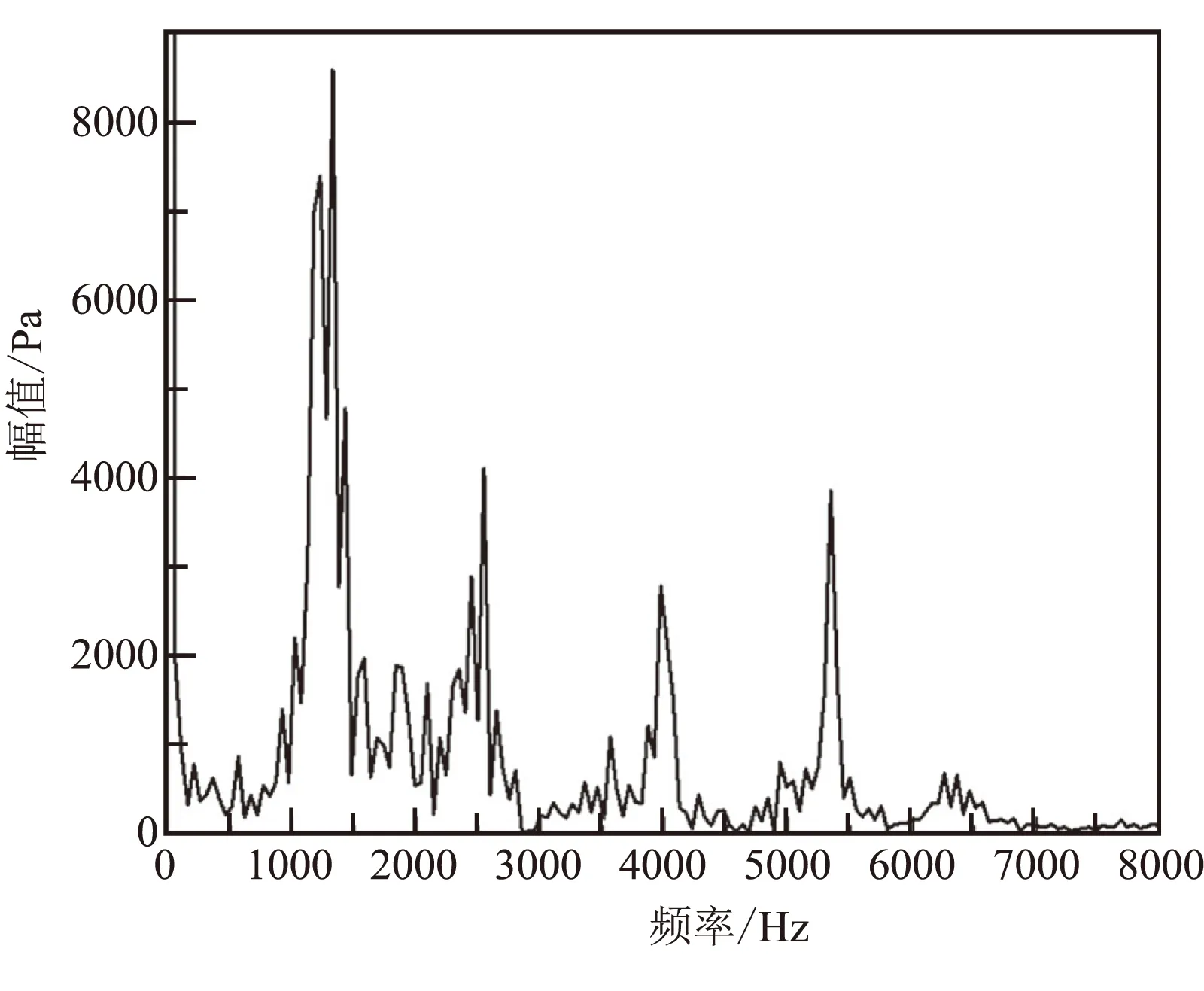
(b)凹腔处

阶数头部凹腔处阶数头部凹腔处一阶13211321三阶39653965二阶25412541四阶53375337
4 大长径比SRM燃面动态推移工作过程模拟
对准稳态计算过程中涡脱落过程中压力响应的分析是为研究含包覆层装药动态推移过程中压力响应规律作铺垫。研究燃面推移过程中瞬态内流场,是为探索燃面动态推移过程会对大长径比发动机内涡脱落现象产生的影响,进而判定展开燃面动态推移过程中瞬态内流场计算的重要性。
与准稳态求解模型不同,采用图1计算模型对大长径比固体火箭发动机工作过程中涡脱落现象开展研究,根据不同时刻燃面面积的大小实现燃面处的加质加热,从而模拟燃气的产生,以此来实现燃面推移过程中发动机内流场的计算。由于药柱被包覆,且包覆面为凸曲面,运用自主开发的含包覆层界面识别方法可以很好地实现燃面推移。通过对发动机头部及凹腔位置压力的监测,对燃面动态推移过程中的压力响应规律展开了分析。
由于装药含包覆层,燃面随着推移时间的增加而不断变大,而计算时间步长较小,燃速又较低,所以整个装药燃烧完需要的计算量较大,即监测点保存的数据也较多。为能够更加直观地看出频谱分析的规律,对图像进行了滤波处理,图8即为滤波后监测点的频谱分析结果,表5给出了各阶峰值对应的响应频率统计结果。
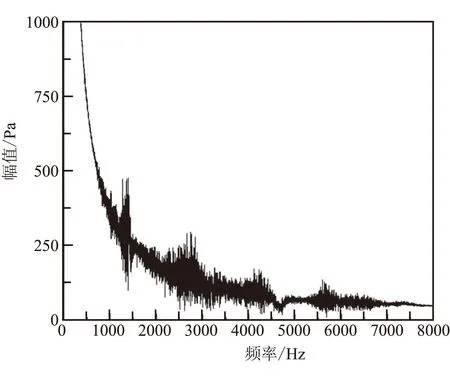
(a)发动机头部
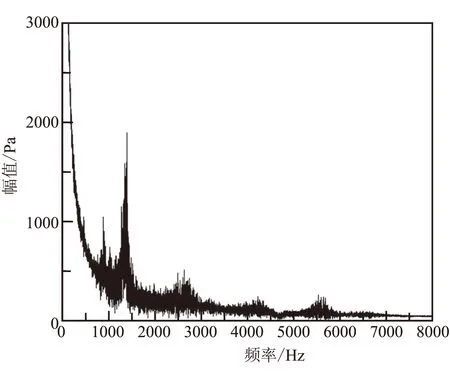
(b)凹腔处
结合图8、表5分析可发现,与传统的准稳态计算不同,瞬态计算伴随着燃面的不断推移,其中不仅有发动机型面及加质的不断改变,还有时间叠加的因素包含在其中,因此整个燃面推移过程中的压力响应与固定型面下的准稳态计算有本质的区别。从图8还可看出,发动机头部和凹腔处压力振荡平均幅值较准稳态计算结果均有大幅度下降。但是两个监测点的各阶峰值对应的响应频率相同,前四阶响应频率分别为1385、2620、4215、5527 Hz。凹腔处的压力振荡幅值比燃烧室头部大,这与准稳态计算得出的规律一致。

表5 燃面动态推移过程中不同监测点的压力振荡响应频率对比
5 瞬态与准稳态计算结果对比
准稳态计算已经成为国内外研究人员通用的一种计算发动机内流场的方式,其流场的准确性也已得到验证。但装药燃面动态推移可能会对发动机内流场产生一定的影响,因此本节将会对燃面动态推移结果以及准稳态结果展开对比,分析二者的相同点与区别。
燃面动态推移过程中关于压力的频谱分析是对发动机整个工作过程而言的,因此选取瞬态计算过程中与型面A和型面B相对应时刻的燃面展开分析,并且与准稳态计算结果进行对比。
图9为型面A、B条件下不同监测点的瞬态和准稳态压力计算方式下的频谱分析图。表6统计出了两种不同型面下的监测点的瞬态和准稳态一阶响应频率。结合图9、表6可看出:
(1)燃面动态推移过程的模拟不会改变监测点压力频谱分析曲线的变化趋势,但是会令压力峰值及其对应的响应频率产生数值上的差异。此规律从侧面验证了瞬态计算结果的合理性,且具有一定的参考价值。
(2)瞬态计算对凹腔压力振荡产生的影响较大,型面A条件下瞬态计算凹腔处的一阶峰值比准稳态要高出2000 Pa,型面B条件下瞬态计算凹腔处的一阶峰值比准稳态要高出7000 Pa。
(3)瞬态和准稳态压力频谱分析结果都表明,凹腔处的压力振荡幅值比发动机头部要大,其中一阶峰值在数值上尤为突出。
(4)初始燃面下的准稳态计算中监测点压力一阶峰值对应的频率均为1100 Hz,该燃面下的瞬态计算结果中压力一阶峰值对应的频率均为1150 Hz;型面B条件下的准稳态和瞬态计算中监测点一阶峰值对应的频率分别为1321 Hz和1200 Hz。结果表明,燃面推移带来的一阶响应频率的改变是非线型的。
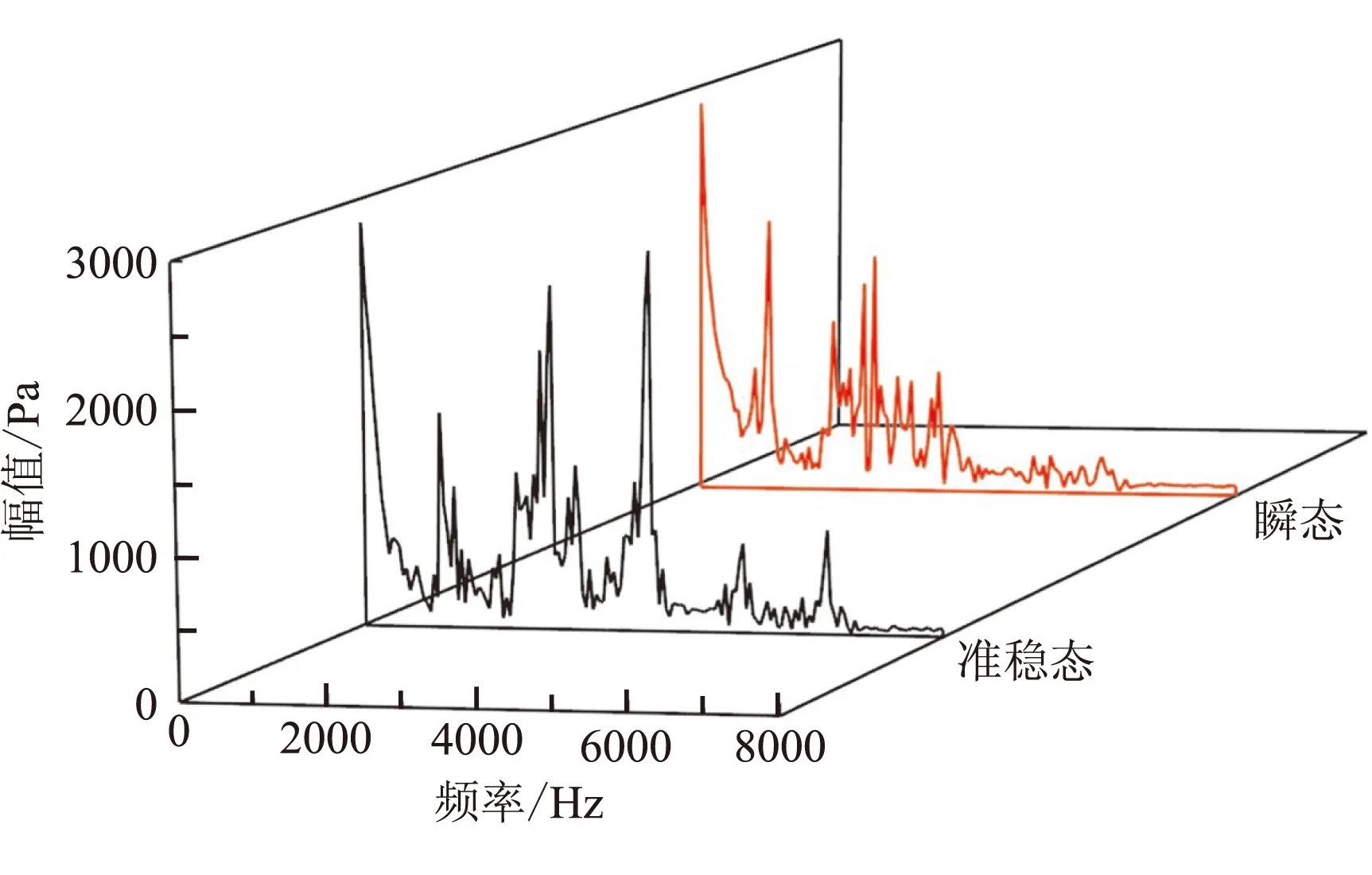
(a)型面A,头部
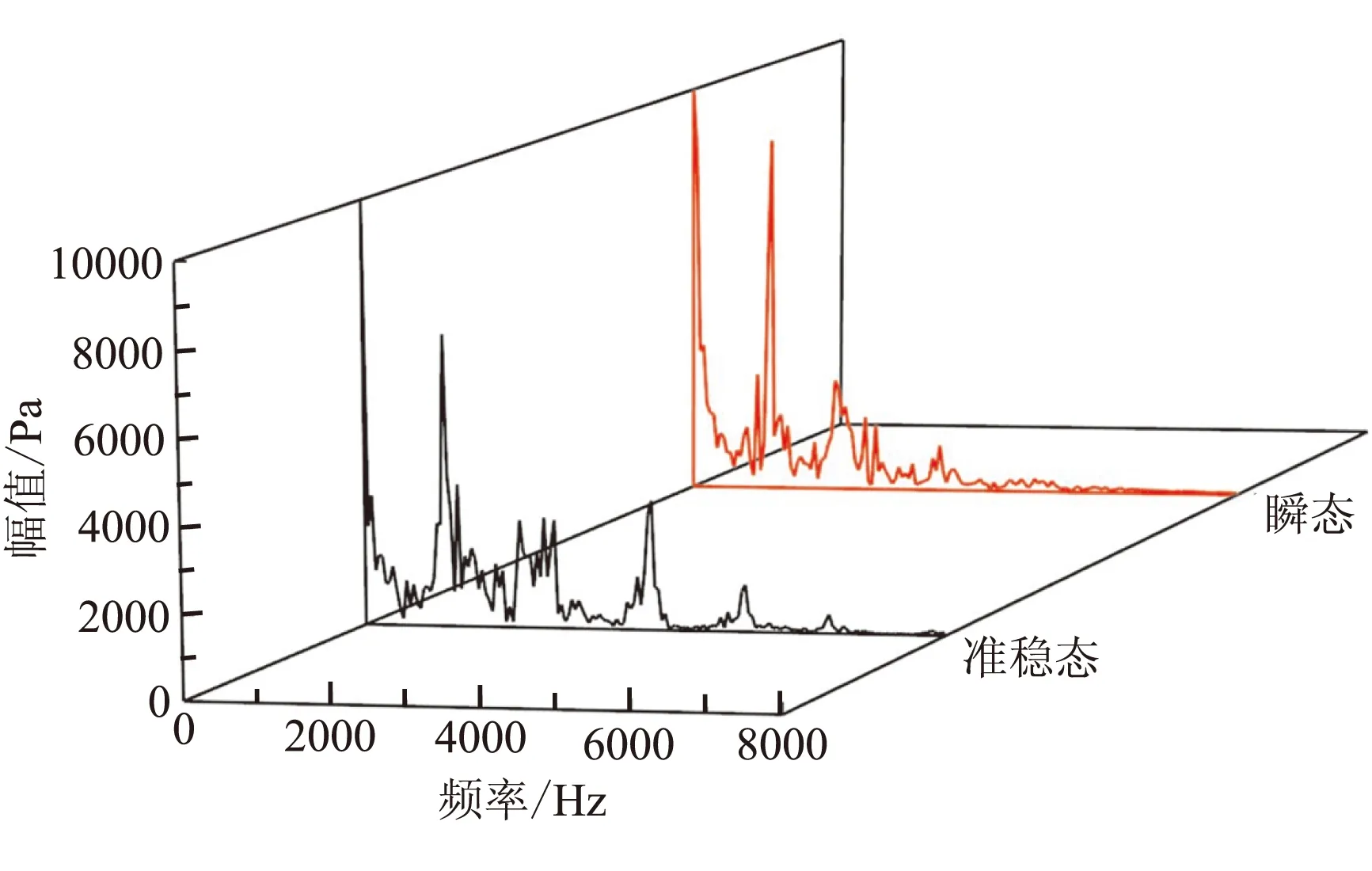
(b)型面A,凹腔处
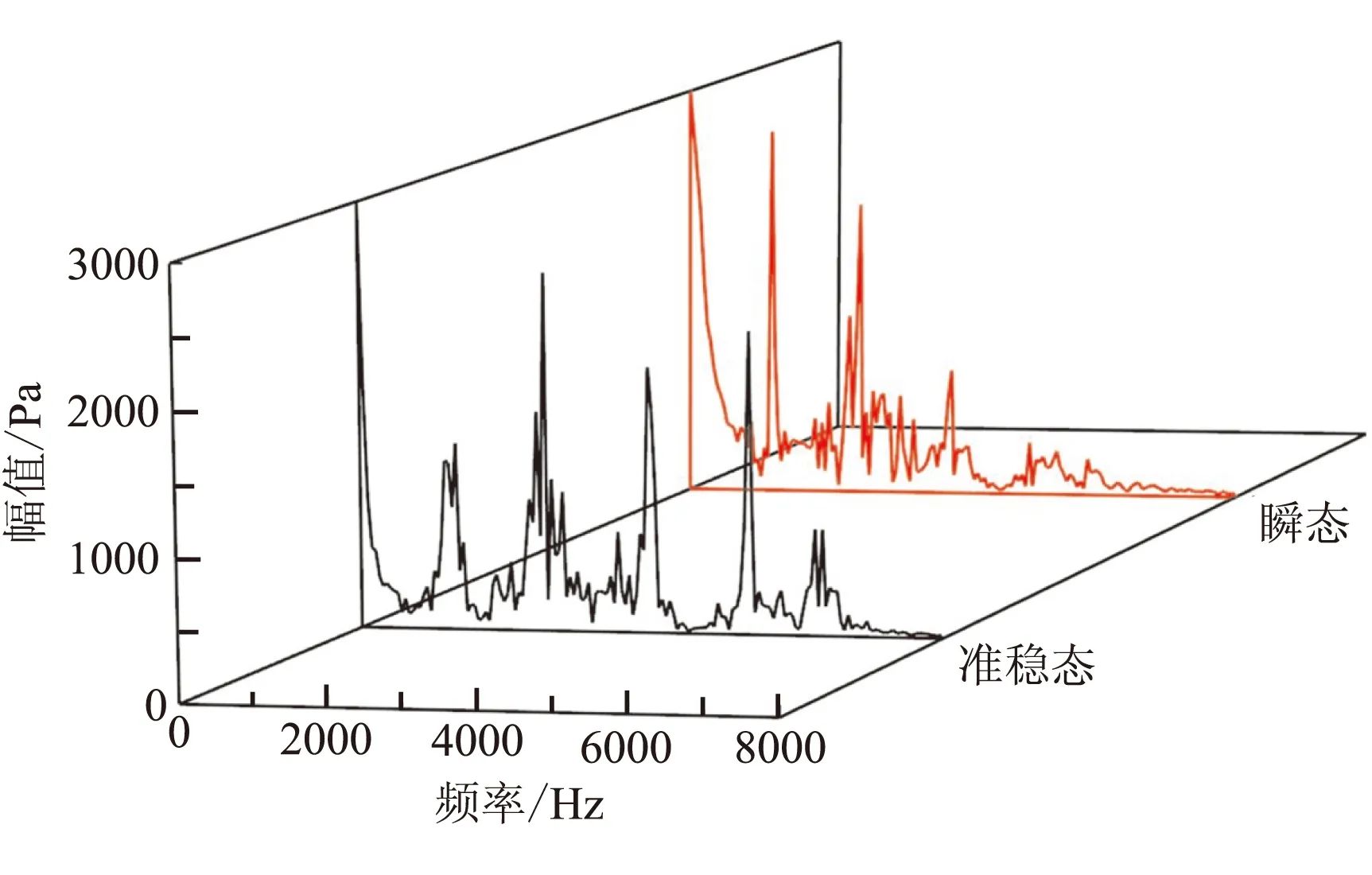
(c)型面B,头部
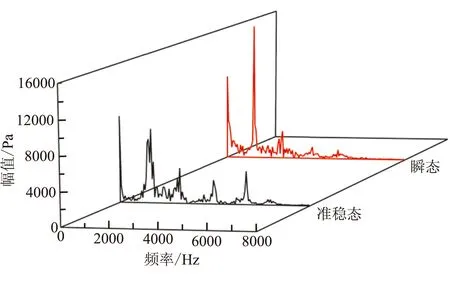
(d)型面B,凹腔处
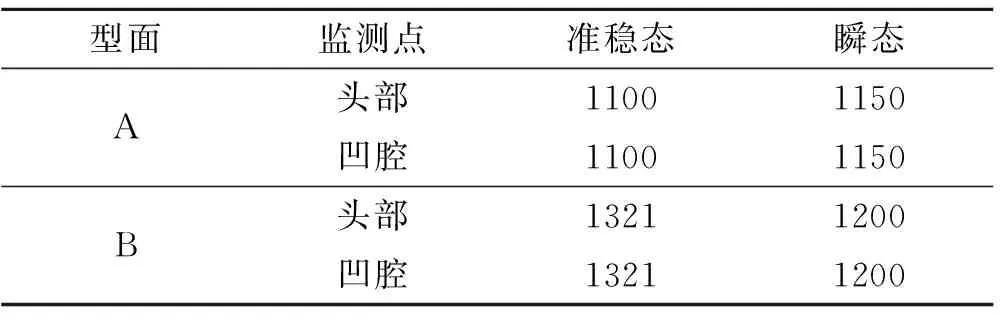
型面监测点准稳态瞬态A头部11001150凹腔11001150B头部13211200凹腔13211200
6 结论
(1)温度(音速)会对发动机内的压力响应频率产生较大影响,其响应频率的大小与温度呈开方倍关系。
(2)针对发动机内同一位置监测点,与准稳态计算结果相比,燃面动态推移过程中的压力响应幅值较小,大长径比发动机工作过程中不仅有由于燃面推移导致的型面不断改变,且还有较长的时间累积过程,因此压力频谱分析中幅值有大幅度下降。
(3)通过对不同型面下的瞬态和准稳态FFT结果展开对比,其结果表明,凹腔处的压力振荡幅值比发动机头部要大。瞬态计算不会改变监测点压力频谱分析曲线的变化趋势,但是会令压力峰值及其对应的响应频率产生数值上的差异,且燃面推移带来的一阶响应频率的改变是非线型的。
