2017年全国高中数学联赛第9题探源

●

(游埠中学,浙江 兰溪 321106)

2017年全国高中数学联赛试题第9题构思巧妙，朴实无华，以常见的含绝对值的二次不等式为背景，考查推理论证能力.试题背景深刻，解法多样，是一道值得探究的“中国好题目”．

1 试题呈现

例1设k，m为实数，不等式|x2-kx-m|≤1对所有x∈[a，b]成立．证明：b-a≤22.

(2017年全国高中数学联赛试题第9题)

2 解法探究

解法1(参考答案)令f(x)=x2-kx-m，其中x∈[a，b]，则f(x)∈[-1，1]，从而

f(a)=a2-ka-m≤1，

(1)

f(b)=b2-kb-m≤1，

(2)

fa+b2=a+b22-k·a+b2-m≥-1.

(3)

式(1)+式(2)-式(3)×2,得

(a-b)22=f(a)+f(b)-2fa+b2≤4,

故

b-a≤22.

让人感到疑惑的是，怎么想到列出式(1)～(3)？笔者将在后面对本题的背景作一简要分析．

解法2(换元法)令x=b-a2cosθ+b+a2(其中θ∈R),则原不等式转化为

(b-a)28cos 2θ+b2-a22-b-a2kcosθ+

3b2+3a2+2ba8-a+b2k-m≤1,

于是，只需满足

(b-a)28cos 2θ≤1,

故

b-a≤22.

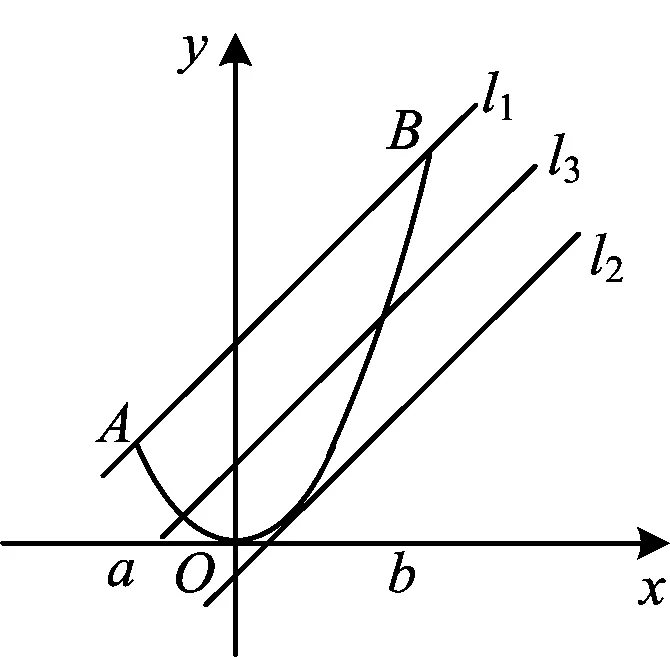
图1

解法3(数形结合法)设y1=x2，y2=kx+m，则|y1-y2|表示二次函数y1=x2图像上的点(x，y1)与动直线y2=kx+m上点(x，y2)的距离.令d=|y1-y2|，设过点A(a，a2)，B(b，b2)的直线为l1，与直线l1平行且与抛物线相切的直线为l2，与直线l1，l2等距的直线为l3(如图1)，这3条直线的方程分别为

l1:y=(a+b)x-ab,

l2:y=(a+b)x-(a+b)24,

l3:y=(a+b)x-a2+b2+6ab8,

则mink,m∈Rmaxx∈[a,b]d=a2+b2+6ab8-ab=(a-b)28.

由题意，只需满足(a-b)28≤1,因此b-a≤22.

我们称多项式(a+b)x-a2+b2+6ab8为函数y=x2的最佳逼近多项式．

解法4(构造平口单峰函数,改进解法3)构造函数f(x)=x2+λx，使得f(a)=f(b)，易知

λ=-(a+b),

则原不等式转化为

|x2-(a+b)x+(a+b-k)x-m|≤1．

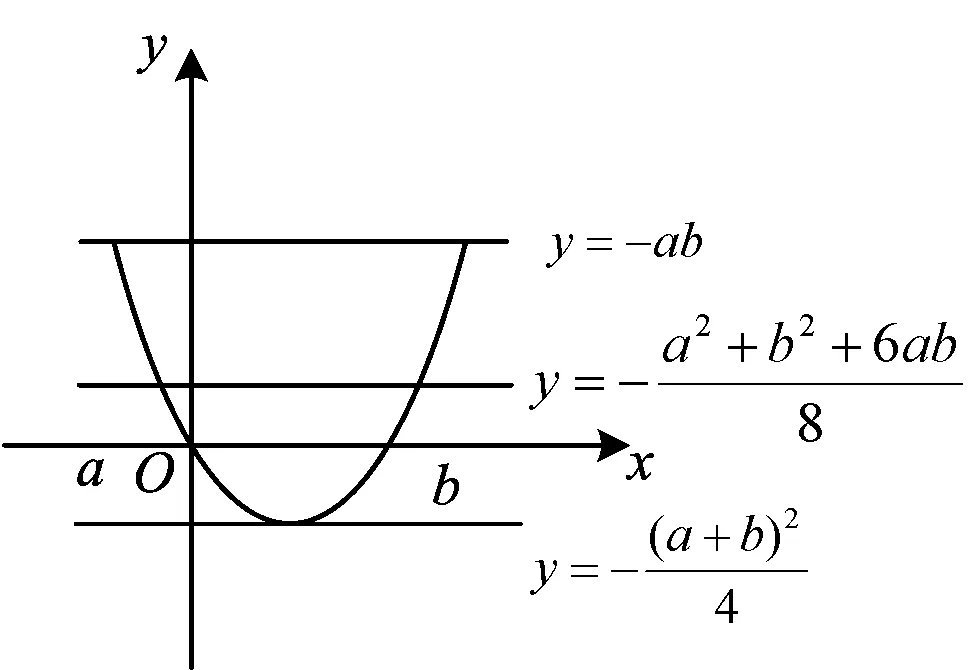
图2

设y1=x2-(a+b)x，y2=-(a+b-k)x+m，则|y1-y2|表示二次函数y1=x2-(a+b)x图像上的点(x，y1)与动直线y2=-(a+b-k)x+m上点(x，y2)的距离.令d=|y1-y2|，函数y1=x2-(a+b)x的值域为-(a+b)24,-ab(如图2).根据解法3的思路，得

mink,m∈Rmaxx∈[a,b]d=(a+b)24-ab2=(a-b)28,

由题意，只需满足(a-b)28≤1,故b-a≤22.

通过解法3和解法4，可知当b-a取到最大值22时，k=a+b,m=-a2+b2+6ab8.

3 背景探源

本题涉及双层最值问题，即

mink,m∈Rmaxx∈[a,b]|x2-kx-m|,

其背景是二次形式的切比雪夫多项式2x2-1(其中-1≤x≤1)．下面证明

maxx∈[-1,1]|x2+a1x+a0|≥maxx∈[-1,1]x2-12=12.

令x=cosθ(其中θ∈R)，则

maxx∈[-1,1]x2-12=12max|cos 2θ|=12.

假设存在二次项系数为1的二次多项式Q(x)，使得

maxx∈[-1,1]|Q(x)|

那么令P(x)=Q(x)-x2-12,则P(x)是一个次数不超过1的多项式．

由假设可知-12

P(-1)=Q(-1)-12<0,

P(0)=Q(0)+12>0,

P(1)=Q(1)-12<0,

根据介值定理知P(x)应当具有两个零点，而P(x)至多是一次多项式，故假设不成立．

这表明任何二次项系数为1的二次多项式f(x)在区间[-1，1]上的最大值都满足

maxx∈[-1,1]|f(x)|≥12,

而切比雪夫正交多项式x2-12是最大值最小的多项式．

一般地，在区间[-1，1]上，最高次项系数为1的所有n次多项式中，与0有最小偏差的多项式为切比雪夫多项式Tn(x)=12n-1cos(n·arccosx)，其偏差为12n-1，具体证明可参见文献[1]．

现在我们可以解释解法1．先说明为什么取x=a，b，a+b2.本题的最终目标是要证明b-a≤22.要使最终的等号取到，所列的式(1)～(3)要同时取到等号，怎样能保证呢？联想到切比雪夫多项式2x2-1 (其中-1≤x≤1)，当x=-1，0，1时，|2x2-1|取到最大值1．把本题的区间[a，b]变换到[-1，1]，令

t=2b-ax-b+ab-a(其中-1≤t≤1),

容易看出：当t=-1，0，1时，恰好对应x=a，a+b2,b.

然后注意到当t=-1，0，1时，多项式2t2-1的值分别为1，-1，1，其规律是正、负、正，即最大、最小、最大．因此，当对应的x∈[a，b]时，有f(a)≤1，fa+b2≥-1,f(b)≤1.

最后通过式(1)+式(2)-式(3)×2消去k，m，得到结果．

4 性质探究

下面给出一条与系数有关的性质：设f(x)=ax2+bx+c，其中[-1，1]，若|f(x)|≤1，则|a|≤2．

证明由a+b+c=f(1),

a-b+c=f(-1),

c=f(0),解得

a=f(1)+f(-1)-2f(0)2,

于是 |a|= |f(1)+f(-1)-2f(0)|2≤

|f(1)|+|f(-1)|+2|f(0)|2≤2,

当且仅当|f(1)|=|f(-1)|=|f(0)|=1时，等号成立，此时f(x)=2x2-1恰好是切比雪夫多项式．

一般地，设函数f(x)=anxn+an-1xn-1+…+a1x+a0，若对任意实数x∈[-1，1]，|f(x)|≤1，则|an|≤2n-1，具体证明可参考文献[2]．

令t=2b-ax-b+ab-a(其中-1≤t≤1),则原不等式转化为

(b-a)24t2+b2-a22-b-a2kt+

(a+b)24-a+b2k-m≤1.

根据前面讨论的性质，立即可知

(b-a)24≤2,

即

b-a≤22.

此类问题也曾出现在2010年全国高中数学联赛中：

例2已知函数f(x)=ax3+bx2+cx+d，当0≤x≤1时，|f(x)|≤1，试求a的最大值．

(2010年全国高中数学联赛试题第9题)

分析令t=2x-1，其中t∈[-1，1]，由题意|f′(x)|≤1，可转化为

34at2+32a+bt+34a+b+c≤1,

根据性质可知34a≤2,故amax=83.

由此可见，例1和例2是同源题．认清试题的本质和来源是多么重要啊！

5 变式应用

变式1已知a，b∈R，f(x)=|2x+ax+b|.若对任意的x∈[0,4],f(x)≤12恒成立，则a+2b=______.

(2018年浙江省诸暨市高三数学期末试题第17题)

分析令t=x-1,则t∈[-1,1]，从而

|at2+(2a+2)t+a+b+2|≤12

恒成立．根据切比雪夫多项式x2-12≤12(其中-1≤x≤1),易知a=-1,b=-12，故a+2b=-2.

变式2若对于任意的x∈[-1，1]，恒有|4x3-ax|≤b(其中a，b∈R)成立，则当b取到最小值时，实数a的值为______．

(2018年浙江省温州市六校联考试题第17题)

分析根据切比雪夫多项式

|cos 3θ|=|4cos3θ-3cosθ|≤1，

立即可得bmin=1，此时a=3．

变式3设函数f(x)=|x-ax-b|，其中a,b∈R,若对任意的实数a，b，总存在实数x0∈[0，4]使得f(x0)≥m成立，求实数m的取值范围．

(2015年浙江省数学学考试题第34题)

分析令t=x-1,则t∈[-1,1],由题意，本题实质是求

mina,b∈Rmaxt∈[-1,1]|-at2+(1-2a)t+1-a-b|.

由切比雪夫多项式|cos 2θ|=|2cos2θ-1|≤1可知，当a=12,b=14时，

maxt∈[-1,1]|-at2+(1-2a)t+1-a-b|≥

maxt∈[-1,1]-12t2+14=14,

因此实数m的取值范围是-∞,14.