教，为了更好地学——浅谈RMI原理驱动下的高三数列综合复习课

●

(镇海中学,浙江 宁波 315200)

2017年底，笔者应邀在福建省福州市第一中学开设了一节以“数列搭台，函数唱戏”为课题的高三数列综合复习课.本节课以RMI原理为驱动，从函数观点认识数列问题，揭示数列问题的函数本质.人民教育出版社章建跃博士在点评中给予了充分的肯定，并就高考复习课的评价标准、高考综合复习课的“综合”含义、高考综合复习课的核心是思维等方面进行了详尽地论述.笔者受益匪浅，在此与大家分享笔者的实践与思考.

1 RMI原理简介

所谓RMI原理，是“关系—映射—反演”原理的简写,徐利治先生在《数学方法论》中谈到：RMI原理是一种分析处理问题的普遍原则，它属于一般方法论性质范畴的一种工作原理，普遍适用于解决数理科学与工程技术科学方面的有关问题.在生活中，女性化妆的完成，遵循的是一条“人的脸部→像的脸部→像画完妆→人画完妆”的路线.这一日常行为的过程，本质上蕴含着一个重要的思维模式——RMI原理，即关系→映像→反演[1].

2 RMI原理在教学中的实践

本节课是在学生已经完成数列一轮复习后开设的综合复习课.何为综合复习课？章建跃博士在点评中的这一发问，引起了大家的思考,他认为：一方面，教师准备综合复习课时需要有知识的综合贯通、观点的归纳、思想方法的相互联系，正所谓联系出思想；另一方面，学生学完这节课后，能够提高从不同角度看问题并选择最优方法解决问题的能力.

因此，在综合复习课中，教师在授之以鱼的同时，更需要授之以渔.而RMI原理作为重要的思维模式，笔者希望借助数列问题来阐明其原理的运用过程，从而通过教师的教促使学生触类旁通，更加主动地进行学习，最终使得我们的高考复习更具系统化.

2.1 以本为本，重识数列问题

数学教学是使静态的书本知识内化到动态的学生数学思维中去思考和认识的过程，只有在教学中关注知识产生的背景、关注数学的来龙去脉，才能让学生感受到数学是自然的，从而自主提出问题.这样不仅让学生学习数学变得轻松，而且有利于激发学生的探究意识[2].

在人教A版《数学(必修5)》数列章节中，定义完数列的概念之后就重点描述了数列与函数的关系：数列可以看成以正整数集(或它的有限子集{1,2,…,n})为定义域的函数an=f(n)，当自变量按照从小到大的顺序依次取值时，所对应的一列函数值．反过来，对于函数y=f(x)，如果f(i)(其中i=1,2,3,…)有意义，那么我们可以得到一个数列f(1)，f(2)，f(3)，……

学生在重拾课本的过程中，逐步明确了本节课的主题.顺势，笔者抛出上述第6)个函数影子，以此作为引例.

正所谓实践出真知，通过这个引例让学生初步体会用函数观点解决数列问题的优越性.

2.2 以熟题为例，联系函数获新知

《普通高中数学课程标准(2017版)》提出：有效的数学学习活动不能单纯地依靠模仿与记忆，动手实践、自主探究与合作交流是学生学习数学的重要方式[2].在学生的心中埋下函数观点的种子后，笔者以常见的问题为例，引导学生归纳用函数观点解决数列问题的基本步骤，从而体会RMI理论在数学解题中的实践与应用.

例1设等差数列{an}的前n项和为Sn，已知S5=20，S10=-10．

1)求S9的值；

2)求使得n·Sn最大的序号n的值．

(2013年全国数学高考新课标卷Ⅱ理科试题第16题改编)

第1)小题，学生给出了两种解答方法：

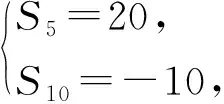
第2)小题，即求数列{-n3+9n2}的最大项是第几项.学生同样给出了两种解答方法：

解法1令bn=-n3+9n2，通过数列单调性的定义，相邻项相减作差，得到数列{bn}在1≤n≤6,n∈N*时单调递增，在n≥7,n∈N*时单调递减，故使得n·Sn最大的序号n=6．

解法2令f(x)=-x3+9x2，通过求导，得到f(x)在(-∞,0]上单调递减，在[0,6]上单调递增，在[6,+∞)上单调递减.考虑到g(n)=-n3+9n2是特殊的函数，其在1≤n≤6,n∈N*时单调递增，在n≥7,n∈N*时单调递减，故使得n·Sn最大的序号n=6．

通过这个问题的解决，让学生熟悉用函数观点解决数列问题的基本步骤：首先，将数列问题转化为特殊的函数问题;其次，用函数方法解决这个函数问题;最后，将得到的函数结论反演成数列结论.这就是RMI原理在数学解题中的应用.

维果斯基在最近发展区理论中指出：教学应着眼于学生的最近发展区，为学生提供带有难度的内容，调动学生的积极性，发挥其潜能，超越其最近发展区而达到下一发展阶段的水平，然后在此基础上进行下一个发展区的发展.本题的第2)小题就是带有难度的内容，如何有效地解决学生的这个疑问，是突破本节课难点的关键.

此时，学生们陷入了沉思.

既然从代数角度无法解释，笔者引导学生从几何角度进行思考.于是就有了如下的解释：等差数列{an}的图像是对应一次函数f(x)图像上的散点.如果将定义域n∈N*拓展到x∈R，那么(5,f(5)),(5.5,f(5.5)),(6,f(6))这3个点都在一条直线上，满足

f(5)+f(6)=2f(5.5),

于是

a5+a6=2a5.5，

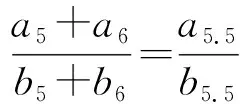
在学生熟悉的问题上设置变式，引发学生思考，并通过生生探究、师生交流共同解决问题，提升认识，这是高三复习课的正确打开方式.同时，通过这一问题的解决，让学生进一步体会运用函数观点解决数列问题的优越性，并对RMI原理的应用有更直观地认识.

(人教A版《数学1(必修)》第83页第二章复习参考题B组改编)

笔者在巡视教室的过程中，发现很多学生毫无头绪，只是简单地列出了

S19=a1+a2+…+a19，

还有些学生则在进一步代入通项公式后，发现了其中的规律，结果如下：

S19=a1+a2+…+a19=

生2：上述式子中，首尾两项相加为定值，即

一般地，

从而通过“倒序相加求和”的思想方法，得到

可得S19=19.

正当学生们笑逐颜开、不断称赞生2时，笔者带领学生进一步挖掘问题的内涵，继续抛问.

学生似乎还未从刚才的数列问题中反应过来.

生3：f(x)+f(-x)=2，说明函数f(x)的图像关于点(0,1)中心对称.

师：这一函数中的性质与本题数列中的结论有何联系呢？

师：函数的对称性与等差数列的“倒序相加求和”思想方法又有何联系呢？

生6：其实不只是等差数列，只要任意数列的图像是中心对称图形，它都可以用倒序相加法求和.

上述几位学生一系列的回答将本节课推向高潮，学生们都情不自禁地鼓掌.相信这样的掌声是发自学生内心的，是对原有的旧知识能获得这样的新认识感到惊叹.课后，有一位学生向笔者反馈：数列与函数的关系以前略知一二，但没想到联系如此紧密，用函数的观点认识数列问题太神奇了，太有意义了！

同时，在RMI原理驱动下，用函数观点认识、思考、解决数列问题的模式已在学生脑海里留下了深刻的烙印.

例4已知递增数列{an}满足

其中a>0，且a≠1,求实数a的取值范围．

正当课堂氛围达到高潮之时，例4恰到好处地起到了“降火”的作用.学生们的思考再次回归理性，理解数列作为特殊的函数，其特殊性到底在哪里.

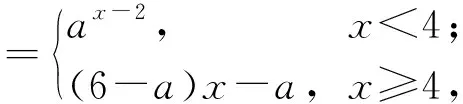
解得1

很显然，学生们忽视了数列图像是一系列散点的特殊性，在n=4这个间断处只需满足a3

解得1

2.3 水到渠成，揭示RMI原理内涵

至此，本节课也接近了尾声，笔者带领学生从基本思想方法和基本活动经验两方面对本节课进行了归纳总结.正当学生们意犹未尽时，笔者顺势提出RMI原理的概念与它在本节课中及今后数学解题中的应用，可谓水到渠成.具体用如下框图展示：

最后笔者以笛卡尔的一句名言结束了本节课：“我们所解决的每一个问题都将成为一个范例，以用于解决其他的问题.”

3 点评与思考

章建跃博士在点评环节，从具体课例出发，就高考复习课的评价标准、高考综合复习课的“综合”含义、高考综合复习课的核心是思维等方面进行了详尽地论述.笔者感动于章博士对数学知识的认真严谨、对数学教学的研究至深、对数学事业的激情投入.现将章博士的观点及对本节课的点评内容整理如下，与同行们分享、交流，也促使自己进一步反思.

章博士认为复习课、高考复习课、高考综合复习课是层层递进的关系.高考综合复习课没有落脚点，没有基本线索，每一个人都是不一样的.

3.1 高考复习课的评价标准

本次公开课的目标是高考复习，就需要功利性，要为高考获得高分努力奋斗，这个目标不是低级的，这是授课教师的责任.至于高考复习多久，这是一个值得讨论的问题.但是只要进入高考复习，我们就要以此作为评判标准，即复习的效果是否有利于高考题的解答，能否实现高考得高分.高考复习要落实以下24字方针：能力立意，基于测评；问题导向，夯实双基；精准高效，大幅提分.

基于以上目标，“是否瞄准高考，讲高考要考的东西”便成为衡量高考复习课的基本标准.具体怎样做呢？章博士认为基本的方法就是认真分析近几年的高考题.当然，分析高考题要有结构分析，即从每一道题目涉及的知识、方法、思想、能力角度形成有结构的分析.并在此基础上形成有结构的复习方案，其中包括复习目标、复习内容、过程设计、效果检测，尤其是效果检测，影响着课堂的精准度和效益度.

“数列搭台，函数唱戏”作为本节课的课题，目标明确，很好地体现了“综合”两个字.它是利用一次函数、二次函数、反比例函数、指数函数等性质来研究数列的相关问题.其中，在具体用函数的观点解决数列问题的过程中，需要处理好“思想方法的一致性和需要注意的问题”之间的关系.高考中，能用函数观点处理的数列问题，往往所涉及的函数是“好函数”.

3.2 高考综合复习课的“综合”含义

章博士认为有些教师在这个阶段只选难题、巧题，这是不可取的.“综合”两字含义从大的方面来看应该是：观点的归纳、思想方法的相互联系、知识的综合贯通[3].正所谓联系出思想，只有关注到了联系，知识结构才能够通道顺畅、应用自如，从而提高学生从不同角度看问题并选择最优方法解决问题的能力.

本节课围绕“数列是特殊的函数”，对“到底特殊在哪里”进行思考，由此设计教学过程，然后选择问题进行布局，布局的内容就是一些考点.整节课通过函数与数列的比较来实现知识的综合贯通，教师润物无声地将学生头脑中有关数列与函数的知识拿出来，通过比较，让其变得清晰、可辨别，最终使得知识可利用.这也是判断一个人数学认知结构是否优良的重要标准.

函数与数列有相同的地方，也有不同的地方，如果是基本初等函数，因为都是“好函数”，都是光滑的，比如例1中涉及的三次函数就可以通过求导得到最大值.这时，以这个最大值为导向，求出数列中最大项的方法是可行的.

对于例2的等差数列性质问题，如果等差数列有9项，那么最中间那项就是这9个数的平均数，这9个数的和就转化为这个数的9倍.然后有10项该怎么办？事实上，这里涉及到等差数列的重要性质.教师在此过程中，发问道：如果将a5+a6强行化简，该怎么办？有个学生小声说：a5.5.这个过程处理得快了些，有待商榷.事实上，a5.5就是a5和a6的等差中项，而等差中项在等差数列中的含义是非常广泛的，它就是平均数的概念.因此，在教学过程中，我们应该从等差数列的基本性质出发，深刻理解“等差”二字，并思考如何在此基础上生发变化，反过来，又做到万变不离其宗.

例3则是对倒序求和的灵活应用，其中精心设计的教学过程值得大家学习.同时，对称思想是现代数学的核心思想之一.

3.3 高考综合复习课的核心是思维

高三综合复习课应该加强思维有序性的教学，让学生有逻辑地思考，使其在面对高考题时想到不同的解题方法，让创造性的解题成为必然，而不是撞大运.

1)高三综合复习课的教学目标要明确清晰地表达：在学生已有知识方法的基础上更进一步，让学生形成整章的知识网络，提升分析和解决问题的能力.

2)如何才能使学生想得到，其实就是落实思维的教学.教学不但要有通性通法，还要有针对这道题的特殊方法，而特殊方法往往是简洁的方法.这需要学生在理解题意的基础上实现方法的优化.

3)“少而精”与“多而全”.章博士认为很多教师的日常教学就是多而全，其实是对自己不自信的表现，更是对自己要教的内容没有研究透的表现.实现举一反三、触类旁通是高考二轮、三轮复习的要点.

4)不能以学生水平高作为理由，而把讲难题合理化.我们应该如何处理难题和思维教学、创新能力培养之间的关系？章博士认为适合学生的才是最好的，教师应该充分把握学生的情况，然后选择合适的问题进行教学设计.

5)教师应该想清楚什么该讲，什么不该讲.章博士认为高三综合复习课的程序应该是：学生先读题，理解题意，然后教师进行点评，适当归纳，形成解题思路主线，最后让学生自己做.在此过程中，教师进行巡视，发现问题，有针对性地帮助学生.高考复习题目多，教师讲得多是通病，也是高考复习效果不佳的原因之一.

6)在综合复习阶段，教师要学会判断学生的状态.学生很多时候不是做不到，而是想不到.学生在知识综合处提取不出相应知识，实际上就是认知结构不好，可利用性不好，即能力问题.因此教师应该选择思维含金量高的问题，且在讲解时不要轻易地把窗户纸捅破.教师的智慧在于根据学生的情况，进行启发引导.因此在教学预设时，应做好问题串的设计，然后让学生拾级而上，这是教学设计应该着力的地方.