在研题中感悟数学核心素养
2019-01-16
●
(三门县教学研究室,浙江 三门 17100)
新高考以素养为本,为改进学习而评价,实现了从测试到评价的跃升,突出“教、学、评”一体化的实施策略.新高考以问题解决为价值取向,避免机械记忆、专题模仿、套题训练,考查学生的数学探究、数学发现、数学问题解决和数学创新意识.笔者通过对一道高考题的直观感知、数学抽象、建模分析,研究如何引导学生用数学的眼光观察、用数学的思维思考、用数学的语言表达,从而逐步形成具有数学特征的关键能力与理性思维.
题目已知实数a,b,c,
( )
A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100
B.若|a2+b+c|+|a2+b-c|≤1,则a2+b2+c2<100
C.若|a+b+c2|+|a+b-c2|≤1,则a2+b2+c2<100
D.若|a2+b+c|+|a+b2-c|≤1,则a2+b2+c2<100
(2016年浙江省数学高考理科试题第8题)
1 在问题情境中直观感知,学会用数学眼光观察
格罗滕迪克曾说过:“证明总是源于对问题的洞察力.首先对于相关的实体和概念及其相互关系有一个细微、固执的感觉,然后直接的导引线是从模糊中逐渐显现出来的内在连贯性,以及它与其他已知或预示的内容的一致性——它更确切地指引着一致性,进而与已知结论之间形成更强、更微妙的联系.”在一个综合的情境中,引导学生观察感知问题所蕴含的数学关系,用数学的眼光找到合适的研究对象,然后通过数学对象、运算或关系洞察问题内存的连贯性与一致性.
选项A的条件|a2+b+c|+|a2+b2+c|≤1中,取a=b可以任意大,只需c来调和,可知a2+b2+c2≥100不一定成立.

至于选项D,由|a2+b+c|+|a+b2-c|≤1,可得|a2+b+a+b2|≤1,因此|a|,|b|受限制,从而|c|受限制,对于单项选择题,可以预估选项D是正确的.
数感是关于数与数量、数量关系、运算结果估计等的感悟,可以说数感正是数学的眼光,是细微、固执的洞察力之来源.引导学生经历观察、猜测、计算、推理、验证等活动过程,从数学结构上理解数量关系,培养数感,增强洞察力.
2 在问题解决过程中数学抽象,学会用数学的思维分析
特殊值法是一种通过赋值降低推算难度的解题方法,即在解题过程中选用特殊数据、图形、关系,然后通过简单运算、推理或验证简化问题并得出正确答案或否定错误结论.它具有从特殊到一般的认识规律,既可以帮助学生巧解、速解一些客观题,又可以培养他们的探索、猜想、发现等能力.
从结论入手考虑,寻找结论不成立而满足条件的解.而找出确定的解往往来自于方程,不妨令条件中的两个绝对值都为0,于是将不等式转化为可解的方程.为了使得a2+b2+c2≥100,不妨取a=10.
对于选项A,令|100+b+c|=0,|10+b2+c|=0,解得b=10,c=-110或b=-9,c=-91.
同理选项B中,令|100+b+c|=0,|100+b-c|=0,解得b=-100,c=0.
选项C中,令|100+b+c2|=0,|100+b-c2|=0,解得b=-100,c=0都有解.
对于选项A,B,C都可找到满足条件的a,b,c,但结论并不成立.故选D.
进一步,可以继续将两个二元方程简化为同一个一元一次方程.同样先令a=10,对于选项A,|a2+b+c|=0,|a+b2+c|=0,因为两个方程中关于c都是一次的,可取b=a,方程组转化为同一个关于c的一次方程102+10+c=0,解得c=-110,即a=10,b=10,c=-110.
对于选项B,|a2+b+c|=0,|a2+b-c|=0,因为两个方程中关于b都是一次的,可以令c=0,方程组转化为同一个关于b的一次方程,解得b=-100,即a=10,b=-100,c=0.
同理对于选项C,可得a=10,b=-10,c=0.
故选项A,B,C都不正确.
在综合的情境中,通过赋值把问题转化为方程运算.赋值并非简单地用特殊值代入运算,怎样赋值?为什么要这样赋值?其目的在于探究运算方向、设计运算程序.将不等式转化为方程,进而简化为一次方程.“函数千千万,一次最简单”,数学当然就有算法,算法也许是繁琐的,具体计算过程更繁琐.但是,指挥这些算法的想法却一定是简单的,这是最有威力的[1].引导学生在复杂的情境中把握这些数量之间的关联,把握其变化的脉络,从而形成重论据、有条理、合乎逻辑的思维品质与理性精神.
3 在对数学结论的反思中建立模型,学会用数学的语言表达
问题中的数量关系蕴含着怎样的数学特征?题设与结论之间存在着怎样的逻辑关联?如何构建过渡性命题,探索问题解决的途径?

图1
本题的背景是三角不等式:
||a|-|b||≤|a±b|≤|a|+|b|.
选项A的条件|a2+b+c|+|a+b2+c|≤1中,|a|,|b|可以任意大,只需c来调和.

选项D是形如|x+m|+|y-m|≤1的结构,如图2,点(x,y)在以点A(-m,m)为中心的正方形区域内,当点A在直线y=-x上移动时,|x|,|y|,|m|可以取到所有正数,但是|x+y|≤1.当x=a2+b,y=a+b2时,|a2+b+a+b2|≤1,从而

图2 图3
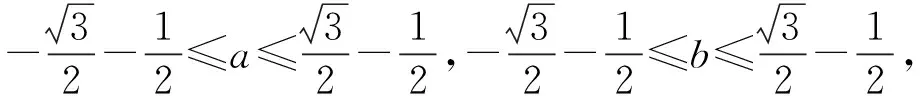
选项A的条件|a2+b+c|+|a+b2+c|≤1与选项D仅相差一个负号,但由选项A得到|a2+b-a-b2|≤1,此时|a|,|b|可以任意大.
通过构建过渡性命题,将复杂的问题转化为熟悉的模型,并用恰当的数学符号语言与图形语言予以表达,进而借助图形的直观性探索解决问题的思路.
本试题通过不等式与方程、一元与多元、代数与几何图形之间的灵活变换,感悟有限与无限的辩证统一.多视角、多层面地研究一道题,可以引导学生经历直观感知、数学抽象、建模分析等合情推理的过程,在估算、赋值转化、建模等数学活动中积累数学思维的经验,在问题解决的过程中形成与发展数学核心素养.
