探寻问题的本质 绽放别样的解法
——一道高考试题的解法探究与思考
2019-01-16
●
(花都区第二中学,广东 广州 510820)
1 题目再现

( )
(2018年全国数学高考卷Ⅱ理科试题第12题)
考点分析该题主要考查了椭圆的离心率.而离心率历来是圆锥曲线的重点考查对象,也一直是高考命题者在命制圆锥曲线试题时的第一视角.此题涉及4个点(两个焦点、一个顶点及点P)、3个量(a,b,c)、1条直线AP和1个特殊三角形.试题的题干通俗易懂,简洁明了,试题的题型和背景熟悉而常见,有着“起点低,入口宽”的特色.
2 思路探究及解答探究
1)题目的已知条件是什么?结论是什么?未知量是什么?用自己的语言表述.
直线PA过点A且它的斜率已知,它的直线方程如何表示;△PF1F2为等腰三角形,∠F1F2P=120°,结合图形分析确认哪两条边相等,还隐含了什么信息;利用椭圆性质,哪些边的长度用椭圆的基本量a,c表示,离心率又是如何表示等.
2)试题的突破口及解题思路:破解本题的关键是点P.方法1:联立方程组,利用方程组求出点P的坐标;方法2:利用参数方程的几何意义求出点P坐标;方法3:作辅助线确定点P的位置及坐标等.
3)思维障碍:题设中没有给出各边长度,只是给出了椭圆的两个焦点,不少学生自然联想到利用椭圆的定义求解,从而造成了思维上的定势.然而问题的关键是“点P不在椭圆上”,不少学生一下子懵了,从而产生思维障碍,且运算繁杂,只能雾里看花,望题兴叹!

图1
解法1(利用平面几何性质和参数方程)依题意可知点A(-a,0),点F2(c,0),由∠F1F2P=120°,过点P作PM⊥x轴于点M(如图1),则
∠PF2M=60°,
从而
设PF2=t,则直线PF2的参数方程为
(1)
因为△PF1F2为等腰三角形,∠F1F2P=120°,所以
PF2=F1F2=2c,

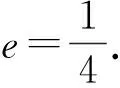
点评利用平面几何性质,巧妙运用直线的参数方程求出点P的坐标,由点A坐标和斜率k列出a与c的关系式,从而求得椭圆的离心率.此方法简单自然,思路清晰,运算量小,让人拍案叫好!
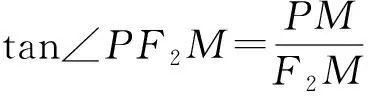
因为△PF1F2为等腰三角形,∠F1F2P=120°,所以
PF2=F1F2=2c,
从而x=c.在Rt△PAM中,
从而
解得
AM=6x,
a=OA=AM-F2M-OF2=4x,
于是
故选D.
点评从图形直观出发,借助椭圆的几何性质,作一条辅助线“高”,一方面确定点P的位置及坐标,利用斜率可列出a与c的关系式求出离心率(详见解法1);另一方面,运用正切函数的定义及直角三角形的边角关系,回避了求点P的坐标及直线AP方程、直线PF2方程的繁琐,此方法快捷、简便.


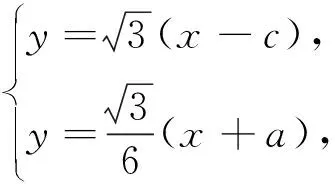
(2)
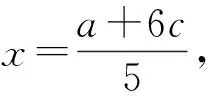
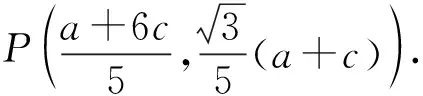
PF2=F1F2=2c,
即
化简得x2-2cx=0.又x≠0,解得
x=2c,
(3)
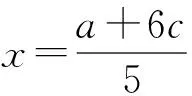
点评由已知条件出发,可知点A和点F2的坐标,分别求出直线AP和直线PF2的方程,通过列方程组求出点P的坐标,再利用椭圆的几何性质和题目的已知条件,转化为关于a与c的关系式,即可求得椭圆的离心率.此方法自然,但运算繁杂,需要学生具备较高的运算能力.
解法4(利用椭圆的几何性质和正弦定理)如图1,由∠F1F2P=120°,可得∠PF2M=60°,从而

于是

在△PAF2中,
即
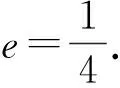
点评利用两直线的斜率可求出两直线夹角的正切,转化为△PAF2的边角问题,再用三角形的正弦定理及椭圆的几何性质,列出关于a与c的关系式,可求得椭圆的离心率.
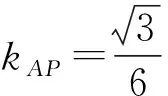
在△PAF2中,∠F1F2P=120°,AF2=a+c,PF2=2c,从而
a2+4ac+7c2.
由正弦定理得
从而
即
化简得
a2+4ac-32c2=0,
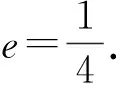
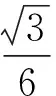
3 教学反思

3.1 优化题设条件
改变题设条件1点P不在椭圆上,△PF1F2为“等腰三角形”改为“等边三角形”,其他条件和结论不变,则上述解法1~5都适合.

改变题设条件2该曲线不是椭圆,改为双曲线,其他条件和结论基本不变.此时,利用直线参数方程会比较简便.

3.2 优化题目结论
将题设条件中椭圆改为双曲线,其他条件不变,将题目结论“求C的离心率为”改为“求C的渐近线方程”.

4 后记
在课堂教学中,重视解题方法的同时也要特别重视运算.对学生解题过程中的运算,教师可通过合理的分析和调控,改变学生“怕算”的心理,使学生养成良好的解题习惯.其次,就是审题.要深刻挖掘题设条件的内涵和外延,选准解题的突破口,克服定势心理,做到“知其所以然”.最后,学生还要细心观察,书写规范,养成严密的推理习惯,最大限度地提高解题能力.
纵观数学高考40年,经过多轮的教材教学改革,高考题型结构由原来的“3选2”变为“2选1”,其中删去的内容便是几何选讲内容.反观2018年数学高考试题发现,适度加强平面几何的教学对提高学生的解题能力大有帮助.总之,用平面几何的“形”渗透到解析几何的“数”,把数的抽象与形的直观有机结合起来,对“减少解题的运算量、优化解题过程”起到事半功倍的作用.这也是命题者最想看到的结果——数形结合.这才是几何的“味道”!
