一节“不同寻常”的试卷讲评课带来的启示
2019-01-16
●
(田家炳实验中学,安徽 临泉 236400)
测试后,教师一般都会用一到两节课的时间讲评试卷.对此,很多教师的做法是先总体评价测试情况,然后挑选学生错误率高的试题;如果时间允许的话,再让学生挑选试题讲解.这样做既可以诊断学生对已学知识的掌握情况,便于调控下一阶段的教学,也可以节省时间,提高讲题效率.近日在一节试卷讲评课上,笔者不经意的一句话,不仅成就了一节“非同寻常”的数学课,而且带来了一些启示,与读者分享.
1 教学片段
片段1
例1若函数f(x)为定义域D上的单调函数,且存在区间[a,b]⊆D(其中a ( ) 这是笔者所在学校高一第二次周练第12题,属于新函数概念题.由于试卷刚考过,学生对它印象深刻. 师:哪位同学愿意到讲台前讲讲这道题? 生1(自告奋勇):因为函数g(x)=x2+m是(0,+∞)上的正函数,所以存在区间[a,b]⊆(0,+∞)(其中a 生2(质疑):你是如何得到g(a)=a,g(b)=b的? 生1:因为[a,b]中的a 生3(表示不认同):因为函数g(x)=x2+m是(0,+∞)上的增函数,且[a,b]⊆(0,+∞),所以 g(x)min=g(a),g(x)max=g(b), 于是g(a)=a,g(b)=b. (大家都认可生3的想法.) 生1:由题意知a2+m=a, (1) b2+m=b, (2) 式(1)-式(2),得a+b=1, 式(1)+式(2),得a2+b2+2m=a+b, 将a+b=1代入,得m=ab. (接下来,生1不知如何继续下去了,大家议论纷纷.) (学生们纷纷鼓掌,课堂气氛热烈.) 生5:由a+b=1得b=1-a,代入m=ab,得 m=a(1-a)=-a2+a, 图1 片段2 例2若方程|x|·(x-4)=m有3个解,则m的取值范围是______. 图2 图3 生8:当x≥0时,x2-4x=m;当x<0时,-x2+4x=m.作出函数y=x2-4x,y=-x2+4x,y=m的图像(如图2),可知-4 生9:图像画错了,结果也错了.函数y=x2-4x与y=-x2+4x的对称轴相同,都是x=2(如图3),可得-4 生10:你画的不就是函数y=|x|·(x-4)与y=m的图像嘛. 生11:不用这种方法也可以.当x≥0时, x2-4x-m=0, (3) 当x<0时, x2-4x+m=0, (4) 易知方程(3)有两个正实数解,方程(4)只有一个负实数解,因此-m>0,Δ=16+4m>0,m<0,解得-4 从教十几年来,笔者经常站在教师的角度,刻板地认为学生只是知识的获取者.在听了学生的讲题后,笔者深受启示. 启示1学生是有创造力的,只是缺乏展示的平台. 说起创造力,似乎很高大上,与学生没有多大关系.其实不然,学生是有创造力的,它只是隐藏在一个角落里不易觉察,只有遇到合适的平台才会发出光芒.当然,学生的创造力在中学阶段更多的体现在对知识的创造性应用上.比如例1,笔者的预设是由题设条件得到两个等式a2+m=a,b2+m=b,进而可知a,b是方程x2+m=x的两个相异正实数根,结合图像求出m的取值范围,对于其他的方法缺乏足够的认知,然而学生让笔者开了眼界:把两个等式作差、作和,再配方,从而问题转化为“在a+b=1条件下,求m=ab的值域”.出乎意料的是,他们居然能够联想到“矩形的周长一定,当这个矩形为正方形时面积最大”这一几何性质简单地解决问题.他们还能用消元法,转化为关于a或b的二次函数求值域问题.这说明:学生是有创造力的,只是缺乏一个合适的平台展示给别人.因此,要相信学生,放手给学生,学生就有可能带给我们惊喜. 启示2学生是有想法的,只是缺乏表达的机会. 在平时的教学中,教师关注的是学生如何掌握知识、如何灵活应用知识.而对于学生有何想法、有何困惑关注得并不多.虽然教师也布置了练习与作业,但从练习与作业中反馈的信息往往只是停留在教师的猜测上,对于学生火热的想法不能及时地参透,造成了“学生有话说不出,有困惑无处讲”的窘境.在这节课上,教师把课堂的主导权给了学生,学生真正成为了课堂的主人,他们参与课堂的热情空前高涨,思维随之活跃起来,质疑与观点也陆续像花一样开放.学生没有了教师主导课堂下的拘束,敢于大胆质疑,敢于表达自己的看法,激发了课堂久违的活力,也使教学出现百家争鸣的景象,这是何等幸事啊!这表明:学生是有想法的,只是我们没有给他们充分表达的机会,或给了短暂的机会又无情地否定了他们的想法.因此,教师应该多站在学生的立场思考课堂教学,真正做到把思考的时间还给学生,把提出问题的权利还给学生,把发表意见的权利还给学生,为学生提供“收放自如、宽严适度”的学习场景和课堂文化[1]. 启示3学生的思维有时不缜密,但可以弥补. 学生讲题,确实能带来不一样的体验与感受,但是也有自身的不足.由于学生对课堂的规律认识不清,对相关知识理解不到位,往往只把解题方法讲出来,而对于如何获取解题方法却涉及甚少,给人一种“从天而降”的感觉.同时,学生受限于自身的思维水平,缺乏对试题的整体把握,难以照顾到知识间的纵横联系,使得解题的思路往往呈现出残缺的状态.就像例2,很多学生看到绝对值,首先想到的是去绝对值、分类讨论.其实,大可不必这样,问题可以看成是两个函数图像的交点问题,只是其中一个函数可化成分段函数而已,这样考虑问题就具有整体性,也易于理解.而这些方法,只有让学生亲身体验,才能品味到其中的滋味,才能在解题中灵活应用[2]. 当然,人多力量大,用在学生主导的课堂上,也是可行的.由于班级的人数众多,一个人思维出现问题的地方,会有其他的学生在这个地方补起来,在学生之间的不断纠错中完成试题的讲解. 启示4教师不是完美的,但可以改进. 说实话,在这节课之前,笔者认为自己的解题思路是完美的,思维是缜密的.但是听了学生的课,笔者自惭形秽:自认为试题的解法单一,而学生给出了不同的解答;自认为学生不善于表达,而学生讨论激烈,争辩不已;自认为学生思维尚幼稚,学生却通过集体的智慧给了笔者很大的震撼.活到老,学到老!同样,对教学的研究,也要活到老,研究到老.教师与学生站的角度与高度不同,认识知识的视角也不同,从而导致认知的偏差.这种偏差可能是我们把学生的水平想得太高了,很多知识不讲学生也能领会,实则不然;也可能是我们把学生的水平想得太低了,很多知识事无巨细、反反复复地讲,其实就是不讲学生也能领悟.因此,我们不能墨守成规,要与时俱进地改进自己的教学理念与方法,与学生“共呼吸”. 总之,一节“不同寻常”的试卷讲评课,让笔者对学生有了新的认识:他们的思维不够缜密,却有潜力与创造力,并且善于表达与交流.也让笔者对自己有了新的认识:人是不完美的,只有不断地学习才能认清与提高自己.

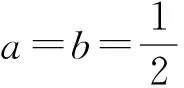

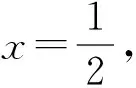

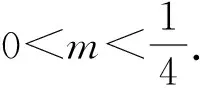

2 启示
