重视背景历经过程 变通思维崇尚理性——由一次周测结果引发的思考

●

(灵璧县第一中学,安徽 灵璧 234200)

1 问题提出

最近笔者所在学校高二年级安排了内容为《数学(选修2-2)》全册(推理与证明、导数、定积分、复数)的周测.面对学生不堪入目的答卷，家长牢骚满腹、无能为力；学生无精打采、唉声叹气；教师愁容不展、无可奈何.通过学科组教研活动，笔者较全面地了解了学生的答题情况和教师的授课情况.本文以部分典型问题为例，给出对相关问题的理解，不足之处，敬请批评指正.

2 案例剖析

例1集合A是集合{1,2,3,…,14}的子集，从A中任取3个元素，由小到大排列之后都不能构成等差数列，则A中元素个数的最大值是______.

多数学生找不到解题的切入点，部分学生缺乏理性思维能力和全局意识导致集合A中存在某3个元素能构成等差数列.

解由题意知，若1∈A，2∈A,则3∉A，令4∈A，5∈A,则6∉A，7∉A，8∉A，9∉A.令10∈A，11∈A,则12∉A，令13∈A，14∈A,此时A中元素个数的最大值为8.

评注题设“由小到大排列”可隐去，学生应该想到对数进行大小排序实现化无序为有序，方便操作.集合A中数的起点和跨度如何确定？为使集合A的元素个数最多，需要其起点低(数值小)、跨度小.以上理应是思维训练有素的学生自然想到的，从本题解答可以看出，多数学生不会思考，即其逻辑推理能力不过关.教师针对基础薄弱的学生应该使用“助产术”启发并助推学生思维有序化，逐步实现思维的优化(如自然数加法的奇偶性判断等)，而对于逻辑思维能力强的学生，教师可引导其探究此类问题是否具有一般性结论.

例2在等比数列{an}中，若a1∈(0,1)，a2∈(1,2)，a3∈(2,3)，则a4的取值范围是______.

多数学生利用等比数列的性质得到

部分学生适度压缩范围得到

解法1设数列{an}的公比为q，则

解法2由条件a1∈(0,1)知

从而

故

于是

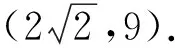
解法3由题意得a1>0，q>0，则

令x=lga1，y=lgq，则

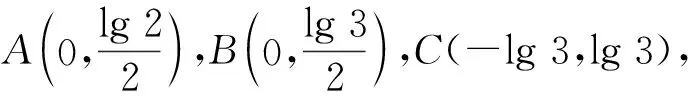
图1

评注相等问题不等化、常数问题参数化、静止问题动态化是考查学生有序化、严谨性思维的有效手段.

例3已知某物体的初速度v0=2，其加速度为a(t)=6t，若该物体做变速直线运动，求它在0～2 s过程中所经过的路程.

问题的解决需要厘清路程、速度、加速度之间的关系，进而代入已知条件求解.遗憾的是，学生弄不清问题的背景和定积分的含义，只能跟着感觉走.部分教师照本(参考资料提供的错误解答)宣科如下：物体做变速运动的速度为v(t)=v0+a(t)=2+6t，当t≥0时，v(t)>0，于是此物体从0～2 s所经过的路程为

以上求解的结果是初速度v0=2.加速度为a(t)=6的匀加速直线运动的物体在前2 s经过的路程.本题物体所做的并非匀变速直线运动，根据其物理背景和定积分的意义，解法如下：

解由题意

则

v(t)=3t2+2.

设物体在0～2 s过程中所经过的路程为s，则

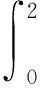
评注素质教育不是喊喊口号，关键在于落实.目前高中数学教学盛行着实用主义文化传统导致的“考什么、学什么、教什么”的应试教育模式所产生的“题海战术”.学科内部、学科之间的内容被肆意割裂，各科教学“各扫门前雪，岂管他人瓦上霜”，导致学生无法形成良好的认知结构，不利于学生对各科知识的理解与深化，更谈不上综合素养的全面提升.各学科处理问题的方式相通，学习方法相似，它们互利共生，齐头并进.其中数学与物理的联系更为紧密，注重数学和物理的结合，沟通两者间知识和思想方法的联系，对拓展学生思路、培养学生创新意识都具有积极作用，同时也符合高考命题“综合化”的改革趋势[1].数理结合是一个人形成和发展数理逻辑思维的重要途径.尽管大部分教师对数学教学渗透物理知识持有积极和肯定的态度，也关注学生头脑中关于物理学科的认知结构，但受教学时间的限制、数学考试方向的引领、数理相关内容理解的缺失、学生对物理问题的理解障碍等导致教师避重就轻、淡然视之.

1)求f(x)的单调区间和值域；

2)设a≥1，函数g(x)=x3-3a2x-2a，其中x∈[0,1]，若对于任意的x1∈[0,1]，总存在x0∈[0,1]，使得g(x0)=f(x1)成立，求实数a的取值范围.

学生牢记求闭区间上连续函数最值的解题步骤，很容易解决第1)小题；学生依稀记得第2)小题可转化为两个函数在给定区间上值域的子集关系，但弄不清谁是谁的子集，只好凭感觉选择.程序化思维是逻辑思维能力的重要体现，它不等同于死记硬背、照搬照抄的解题步骤，关键要理解其本质.如求闭区间上连续函数的最值，要先判断函数的单调性，找出极值点(注意非可导的极值点)，然后将函数的极值和闭区间端点的函数值进行比较，筛选出函数的最值.对于第2)小题，将函数y=f(x)的函数值和函数y=g(x)的函数值进行对比，通过子集的概念可知函数y=f(x)的值域是函数y=g(x)的值域的子集.

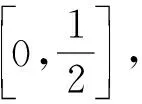
2)g′(x)=3(x+a)(x-a)，由a≥1知，当x∈(0,1)时，g′(x)<0，从而函数g(x)在区间[0,1]上单调递减，且g(0)=-2a，g(1)=1-3a2-2a，即当x∈[0,1]时，函数g(x)的值域为[1-3a2-2a,-2a].由题意得[-4,-3]⊆[1-3a2-2a,-2a]，即

得

评注准确理解题意并合理套用模型是学生综合能力的体现，生搬硬套只会让学生思维僵化，行为教条.教学时要引导学生面对具体情景去分析问题、理解问题和解决问题.对于第2)小题，其导向清晰、提示明显，根据子集的概念，结论显而易见.这说明学生的审题能力和数学抽象均不到位，亟待加强.

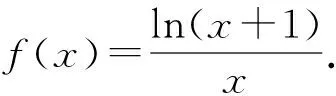
1)判断函数f(x)在(0,+∞)上的单调性；

2)若x>0，证明：(ex-1)ln(x+1)>x2.

证明不等式f(x)>g(x)常见的方法有：①证明结论成立的等价命题f(x)-g(x)>0，即通过充要条件进行等价转化；②证明结论成立的加强命题[f(x)]min≥[g(x)]max(函数y=f(x)的最小值点和函数y=g(x)的最大值点不同，若函数无最值,则用其相应的确界值替代)，即通过不等式的传递性实施过渡.对于含有指数型函数、对数型函数的综合问题，直接求导往往会因为导数形式繁杂而无以为继，常常将指数型函数与对数型函数进行分离，转化为两个函数相应最值的比较.本题分离指数型函数与对数函数,可得

不满足

尝试变形改变函数的结构来调整(变形后的)函数的增减速度，如

仍然失败！学生反复调试后无果，只能被迫放弃.

1)函数f(x)在(0,+∞)上单调递减(过程略).

即

由第1)小题知，函数f(x)在(0,+∞)上单调递减，要证原不等式成立，只需证明：当x>0时，ex-1>x.令h(x)=ex-x-1，h′(x)=ex-1，则函数h(x)在(0,+∞)上单调递增，当x>0时，h(x)>h(0)=0，即ex-1>x，从而

f(x)>f(ex-1)，

即

故

(ex-1)ln(x+1)>x2.

证法2记p(x)=(ex-1)ln(x+1)-x2，其中x≥0,则当x>0时，

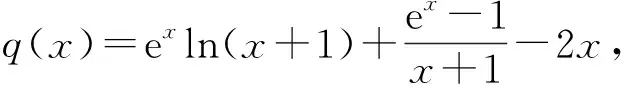
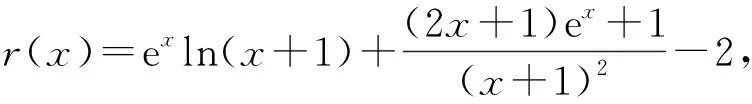
由ex>1，3x2+3x+2>2知

ex(3x2+3x+2)-2>0，

则函数r(x)在[0,+∞)上单调递增，有

r(x)≥r(0)=0，

从而函数q(x)在[0,+∞)上单调递增，有

q(x)≥q(0)=0，

即函数p(x)在[0,+∞)上单调递增，故当x>0时，p(x)>p(0)=0.

评注证法1根据第1)和第2)小题间的传承关系，通过变形构造函数，借助函数的单调性将函数的大小关系转化为自变量值的大小关系；证法2直接作差证明，多次求导不仅需要学生对结果走向的预判，更需要学生有坚定的信念.事实上，既然可用证法1(逆用函数的单调性)，就注定证法2必然可行，只不过证法1从自变量角度切入，证法2从函数值角度切入而已.证法的返璞归真有利于规避教学的“题海战术”，引领中学数学教学方向.数学模型毕竟是理想化的抽象模型，具体问题会更加复杂.解题有法，解无定法，贵在得法.具体问题具体分析，实事求是地选择解题策略与方法正是解题的魅力所在.形同质异的问题能考查学生的阅读理解、分析诊断、反思优化等能力，能较好地甄别出学生的综合素养.

3 教学思考

3.1 深化学习，尝试创新

我们追求教师旁征博引、挥洒自如的教学，期待学生能举一反三、触类旁通地学习.现实却是教师千方百计实施教学设计，学生绞尽脑汁难以消化吸收.这与学生的知识视野、思维水平息息相关，更可能是由教师的综合素养所决定.学而时习之，温故而知新.

《普通高中数学课程标准(2017版)》给出了教师实施课程标准应注意的几个问题：以教师专业标准的理念为指导，提升自身的专业水平，数学教师要努力提升通识素养、数学专业素养、数学教学理论素养以及教学实践能力[2].教育改革的核心在于教师的专业发展，教师专业发展的动力最初来自于内在的需求，主要是“本领恐慌”带来的紧迫感，也可能来自于外部的刺激，如听到一场精彩的报告，拟定了目标和方向等.内心的沸腾是专业发展的必备条件，克服学习上的困难还需要不忘初心，坚持不懈，最后才能养成习惯，渐入佳境.

教育就是在继承中发展、在发展中创生.我们向学生传授的知识、思想方法(载体)，是让学生少走弯路.如现象教学是一种先整体后细节的教学，就是让学生通过对现象(包含特定的教学任务)的探究而形成能力和知识的教学理念和方法[3].如通过解抽象函数所形成的不等式f(x)>m(其中m为常数)的形式化操作让学生明晰单调性的逆用.通过真正地探究、思辨、澄清、升华等过程让学生学会思考，使他们在面对现实世界时，具有能够主动探究、评判和选择的能力.

3.2 重视背景，历经过程

事物在“发展—矛盾—发展—矛盾”中前进.万物皆有联系，如数学的发展推动着物理学的前进，反过来物理学的发展要求迫使数学发展，数学的发展与物理学的发展相互促进、相互影响.但现实教学中，师生缺乏对数理结合的理性思考，将数学贬低为纯粹的工具或技巧，加大了学生数学理解的难度，不利于数学教学质量的提高.教学中要充分挖掘问题产生的历史背景、演变过程、发展趋势，才能让学生从全局角度辩证地分析问题、理解问题.例3中的物理背景并不复杂，高出错率反映了师生在探求问题背景及经历概念抽象过程方面的缺失.

学生在课内主要是聆听与记录，课外多是记忆与练习等，均缺乏必要的数学活动的操作与体验.知识是教学达到教育目标必不可少的工具，尤其在某些阶段(如中学学习)必须精准识记.但它不是出发点，也不是最终追求.知识作为探究过程的重要载体，而学生在探究过程中经历过的惊奇与困惑、彷徨中尝试、否定中问题转化、心理表征与外在表述、成功与失败、反思与理解、评价与延伸等过程方法、情感体验更令其印象深刻，并自然而然地嵌入记忆，形成直觉，转化为综合素养.以后遇到相近或类似问题时，就能自觉或不自觉地提取经历(中的思想方法等)对(别人眼中杂乱无章的)信息进行加工、处理并灵活运用.

3.3 夯实基础，循序渐进

教什么永远比怎么教更重要.爱因斯坦、米山国藏等名家都认为：最有价值的教育是把学校里的知识忘掉后剩下的东西.学生认识事物具有阶段性、层次性，不可能一蹴而就.教师要换位思考，准确理解学生.教学时需要加工教学内容，改进教学方法，切实做到注重基础、强化通性通法，通过“小问题，大道理”实现教与学的以小见大.

3.4 强化变通，崇尚理性

教学就是要“培养具有独立思考能力的、能够适应未来工作需要的、能够进行终身学习的人”[4].教学中除了给学生创造解决实际问题的机会，把从生活现象中抽象、概括、建立数学模型的机会还给学生，让学生在实际应用中领会、掌握科学方法，发展思维能力.还要引导学生对解题过程进行思考，从不同的角度进行分析，对不同的解法及其蕴涵的数学思想、数学方法进行概括和提炼，思考解决问题的心路历程、切入点和思维障碍.学生在遇到具体问题时，实现对问题的能解决、会解决、完美解决.

“数学的本质在于它的自由”(康托尔语).社会、学校、个人等现实教育环境反复考验着教师的立场与意志，不断拷问着教师的教育良心与责任心.立场不坚、意志薄弱的教师形成了“不求有功但求无过”的教学态度与亦步亦趋的教学方法，导致学生思维固化、行动单一.我们期待更为宽松的教育环境，首先要做有理想、有爱心、有能力的教师.