对“一题多解”低效教学的思考——基于一次高三视导听课

●

(大厂高级中学,江苏 南京 210044)

1 背景

开展一题多解教学是培养学生思维灵活性的重要途径之一.不少教师经常通过一题多解进行解题教学，笔者在一次高三视导听课时，一位青年教师甲对高三双周考(两周一次的考试)中的一道试题进行一题多解教学.课后的交流中，教师甲自我感觉已把问题讲得很透彻，学生应该掌握了此类问题的求解方法.但两周之后的双周考中，学生对一道十分类似的问题的解答，错误率很高，表明两周前的那次一题多解教学十分低效.教师甲向笔者诉苦:这类题教了也是白教，原来错了23人，这次错了25人.这引发了笔者的思考，结合听课笔记及与教师甲的交流记录，把教师甲进行“一题多解”教学的片段整理成文，以探究这次一题多解低效教学的形成原因，并给出教学建议，希望能够改进一题多解教学，提高解题教学的课堂实效.

2 题目

例1在平面直角坐标系xOy中,过点P(-4,0)的直线l与⊙C：(x-1)2+y2=5相交于点A,B，若点A恰好是线段PB的中点，则直线l的方程为______.

说明参加考试人数38人，此题出错23人.

说明参加考试人数38人，此题出错25人.

3 教学简录

通过比较教师甲所教同一个班级两次考题(例1和例2)出错的人数，发现学生对这类题目的求解，并没有进步，甚至稍有退步.笔者对教师甲自我感觉良好的一题多解教学产生了质疑，通过回忆并结合当时的听课笔记，及与教师甲的交流记录，将例1的教学片段整理如下：

3.1 错解展示

师：例1错误的人数较多，请一位做错的同学说说自己的解法.

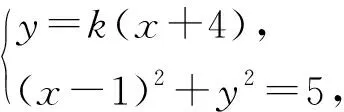
(k2+1)x2+(8k2-2)x+16k2-4=0.

设A(x1，y1)，B(x2，y2),由韦达定理得

根据点A恰好是线段PB的中点，可得2x1=x2-4.下面想求k的值，但感觉计算比较复杂，就放弃了.

(生1 的解法是很多做错学生使用的解法.)

师：生1遇到的困难实际上就是解含有k的三元方程组，只要消去x1，x2就可以了.同学们清楚了吗？

(不少学生点了点头.教师甲当时以为:讲到此处，高三阶段的学生应该能够进行后面的消元求解了.)

3.2 另辟“蹊径”

师：还可以如何设直线方程.

(教师甲想引导学生获得更多的求解方法.)

生2：设直线l的方程为x=my-4.

师：对，这样可以简化运算.

(教师甲当时认为后面的运算可以由学生课后完成.)

师：这道题还可以怎样做？

生3：设点A(x1，y1)，由点A恰好是线段PB的中点，知点B(2x1+4，2y1).根据点A,B都在⊙C上，可以解出点A的坐标，结合点P的坐标，从而可写出直线方程.

生4：过点C向直线PB作垂线，垂足为H，可以得到Rt△AHC和Rt△PHC，从而算出圆心C到直线l的距离CH，然后设直线l的方程为y=k(x+4)，根据直线与圆相交时的弦长公式，就可以求出k了.

师：很好!当算出圆心C到直线l的距离时,求出直线的方程就是圆的弦所在的直线方程，这个问题大家都清楚.

(教师甲并没有追问生4“由Rt△AHC和Rt△PHC求出圆心C到直线l的距离”的过程.)

师：还有其他想法吗？

生5：在△PBC和△PAC中使用两次余弦定理求出∠BPC的余弦值.

生6(对平面几何知识较熟悉)：还可以使用圆幂定理,由圆幂定理可得

再由PB=2PA,可以求出PA，从而得到直线l被⊙C截得的弦长……

师：还有其他想法吗？

生7：可以用直线参数方程的几何意义……

生8：可以重建坐标系,用极坐标方程……

师：对于这个问题，我们得到了8种方法，请同学们课后整理一下.

(课后,笔者与教师甲进行了交流，他认为：这道题已经讲了8种方法，对学生应该有所启发，能够满足不同学生的需要，因此满意地结束了该堂课的教学.)

4 低效教学探因与改进

4.1 “一题多解”教学要详略得当，解决学生的真困惑

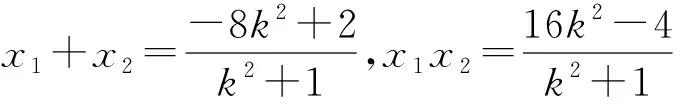
可以引导学生设计出流程，形成小算法：先由韦达定理中第一个式子及2x1=x2-4，得x1和x2(含有k),再回代到韦达定理中的第二个式子,从而得到关于k的一元方程，即可求出k值.再进行方法回顾，指出此方法的使用条件，事实上，此方法在直线和圆锥曲线相交的问题中也可使用，是一种学生容易想到也较为通用的方法.当然，也可以不借助韦达定理，只用求根公式算出两个根x1，x2(含有k)，代入2x1=x2-4，得到关于k的方程，进而求出k的值.在韦达定理使用不顺畅时，这也是一种不错的方法.

本次教学中，教师甲对生1方法的关键处——如何消元求k的值,一带而过；对生4展示的方法关键点“如何由Rt△AHC和Rt△PHC求出圆心C到直线l的距离”浅尝辄止，导致不少学生在解决例2时还是在原来的地方卡壳.“一题多解”教学应在学生的真困惑处浓墨重彩、精雕细刻，在学生能够轻松解决之处可一笔带过，这样才能提高“一题多解”教学的课堂效益.

4.2 “一题多解”教学要在课堂上给学生留足“悟”的时间

这节课中教师甲虽然对例1的8种方法进行了教学，但这些方法连续出现，没有给学生“喘息”的机会，学生缺少体悟和总结的时间，众多的方法变成了过眼浮云，导致低效教学.提高“一题多解”教学实效，解题方法可以少一些，但留给学生整理和体会的时间不能少，要为学生留足将一种方法执行到位甚至再做一遍的时间，否则学生只能被动参与，思维肤浅，不能向纵深处发展，学生的真困难不能得到有效解决.

比如生1采用的方法，在形成了消元求k的流程之后，要给学生几分钟演算的时间，如生4采用的方法，需要给学生一点时间考虑“如何由Rt△AHC和Rt△PHC求出圆心C到直线l的距离”，这都是培养学生数学运算、逻辑推理素养和渗透方程思想的好时机.

4.3 “一题多解”教学要注意方法的比较与个性化选择

课堂上，教师甲除了对生1和生2的方法进行比较之外，没有引导学生发现各种方法的使用条件、优缺点及可适性.解题方法的选择有时带有很强的个性化特征，这一点也在此次教学中被忽视,通过访谈了解到生1在解决例1和例2时都采用了同样的方法，但都没有做出正确的答案.因此进行“一题多解”教学，在方法的比较之后，还要引导学生找到适合自己的方法，并将这种方法理解透彻、执行到位.

比如，生1、生2和生3的方法都比较容易想到，不用作辅助线，遇到的困难是含多个字母的运算；生4和生5的方法中含有对同一个量算两次的技巧，有一定的灵活性；生6的方法要求学生熟知圆幂定理，事实上熟知这个定理的学生较少，这种方法使用的频率也不高；生7和生8的方法主要用到了《数学(选修4)》系列直线的参数设法及圆的极坐标方法，也只是极少数学生能想到和使用的方法.哪种方法最适合学生个体，需要引导学生自己去比较和挑选.

4.4 “一题多解”教学要面向全体,兼顾差异

《普通高中数学课程标准(2017版)》指出：高中数学课程面向全体学生，实现人人都能获得良好的数学教育，不同的人在数学上得到不同的发展[1].在“一题多解”教学时，如何调动学生的积极性，如何兼顾好优秀生、中等生及学弱生，并在各层次学生之间寻求平衡？ 这是一线教师应该经常思考的问题.在教师甲的课堂上，优秀生的思维得到了激活，通过调查了解到有几个优秀生在求解例2时使用了两种以上的方法，但是在教学的后半段，不少中等生、学弱生变成了陪衬，他们没有参与的平台.事实上，“一题多解”也可分层展开教学，不必希望每一个学生都能理解这8种方法.对于大多数学生来说，将2～3种方法理解清楚就可以了.另外，课堂上除了讲清思路，还需将计算进行到底.本节课的后3种方法可以放在课后，由数学兴趣小组的学生在课间讨论中进行(或者教师对优秀生进行个别指导)，这样既有利于优秀学生的发展，又避免了中等生、学弱生无法参与其中的现象.

4.5 “一题多解”教学要有跟进的补偿练习

及时跟进的巩固练习是提高学生数学素养的重要手段之一.回顾教师甲的这次教学，发现后续的补偿练习是缺失的，导致课后这些方法未能得到及时的巩固.上课时学生可能是会的(比如生1的方法)，但是要内化为学生自己的东西还需练习.为了提高“一题多解”教学的效益，后续的补偿练习必不可少.练习题可以由教师选编，也可以由学生编出，哪怕只是改改数据再练习一下，也可以达到巩固方法、提升解题能力的作用.

4.6 “一题多解”教学要让学生在活动中再体验

弗赖登塔尔对“往哪儿指导”这个问题的回答是“到活动中去”[2].解题教学也应如此，不是教师告诉学生解题方法，也不是请优秀生变相地告诉.本节课中的解题方法大多数是告诉式教学，对“学生怎样想到的、为什么这么想、遇到哪些问题可以这样想”等等稍有涉及，但学生没有经历再体验一次的解题活动，无法记住和迁移这种解题经验.从这个角度看，学生遇到例2时仍然出错也就在所难免了.如果学生是被指导着再创造一次解题活动，就会更容易学会、记住和迁移这类问题的解决方法，形成一定的求解此类问题的能力.

著名数学家和数学教育家波利亚给出解题的4个步骤：理解题意、拟定计划、执行计划、回顾[3].本节课教师甲展开的“一题多解”教学，“执行计划”不到位，“解题回顾”缺失，势必导致教学效果较低，如此，在两次双周考中学生对同类题目的解答没有长进也就不足为怪了.有指导的“一题多解”教学也需要遵循波利亚先生提出的4个步骤，方能取得更大的解题效益，达到“会一个，通一类”的效果.

5 结束语

“一题多解”教学是高三数学解题教学的常用手段.教师需要在深刻理解问题的基础上展开教学，同时要充分了解学生的情况，根据学生的情况选择多解中的“多”的度; 在学生的“拥有”和“可能”之间寻求突破，确定详略点; 给学生留足“悟”的时间、再写一遍的时间，这样才能切实发挥“一题多解”教学的效益，有效提高学生的解题能力.