基于活动经验积累的小学数学教学实践研究——以“可能性大小”教学为例

江苏南京致远外国语小学 刘 媛

《义务教育数学课程标准（2011年版）》中关于“数学活动经验”的内涵并没有提出明确的解释，因此引发了众多不同的解读。以下笔者将结合自己所上的一节“可能性大小”公开课，分享在磨课过程中对培养学生数学基本活动经验的认识和感悟。

一、数学基本活动经验的特征

1.个体性特征

【教学片段1】感悟“一定”“不可能”。

教师出示2个同样大小的不透明的袋子，①号袋里放2个红球，②号袋里放1个蓝球、1个黄球，并向学生说明：这些球除了颜色不同外，形状、大小、材质等都完全相同。

师：如果摸到红球算胜利，你会选哪个袋子？为什么？

生：选①号袋，因为两个都是红球，肯定会摸到红球。

小结：口袋里两个都是红球，摸出球的情况是确定的，任意摸一个，就一定是红球。

师：在②号袋里任意摸一个球，会摸到红球吗？为什么？

生：不可能，因为②号袋中没有红球。

片段中学生通过和教师的问答，感悟 “一定”“不可能”，这并不是系统的“数学知识”，而是学生通过观察和思考获得的感受和体验。学生凭借自身的认知经历，对将要发生的结果进行感性的概括，这是学生经历了活动后不自觉形成的新的认识，这里的认识既包含了学生已有的认识，又融入了学生在个性特征基础上所积累到的新知识。

2.多样性特征

【教学片段2】摸球游戏，感悟“可能”。

师：老师把这2个球（1红、1黄）放进口袋里，如果摸到红球，女生赢，摸到黄球，男生赢。这个游戏公平吗？为什么？

生1：个数相同，一半对一半的概率。

生2：红球和黄球各一个，各占50%。

师：从这个口袋中任意摸一个球，摸球前，我们可以预测：可能摸到红球，也可能摸到黄球。也就是，男生赢和女生赢的可能性是相等的。

小组活动：

（1）在口袋里放入1个红球和1个黄球，组员摸球，一共摸10次，摸后放回。

（2）记录员用相应颜色的水彩笔依次整齐地将结果涂在实验记录卡上。

组长汇报摸球结果，板贴展示（如图1）。

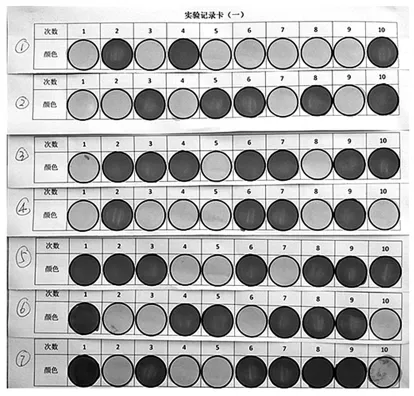
图1

师：出现这些结果合理吗？

小结：在摸球之前，预测摸到红球和黄球的可能性是相等的，但这并不能代表摸球的结果一定相等，因为每一次摸到红球或者黄球的结果是不确定的，所以，出现这些结果都是合理的。

在初授时，本环节的设计被零散地分成了三部分：“装有1个红球和1个黄球的口袋”“装有2个红球的口袋”“装有2个黄球的口袋”，之前的设计多是教师和个别学生对话，相对单一。而对于学生来说，感悟“一定”“不可能”“可能”更需要经验交流的过程，所以经过多次磨课，笔者将本环节修改为上述的“教学片段1”和“教学片段2”。通过两次预判，让学生在群体经验中认识新知，并延伸“出现这些结果是否合理”的追问，充分发挥数学活动经验的多样性特征。

3.发展性特征

【教学片段3】结果比较，内化认识。

观察：结合片段2中实验记录卡的摸球结果，如果竖着看每组地摸球情况，第一次可能摸到什么球？第几次会摸到红球、第几次会摸到黄球，摸球前会知道吗？

追问：如果老师现在再摸一次，结果会是怎样的？

让学生观察、比较全班地摸球情况，分别从横向与纵向角度进行对比，丰富学生对“可能”认识的直观感受。学生的回答步步逼近，不断从小组、班级同学的分享中获得新的认识，促进了学生的数学活动经验从感性水平上升到理性水平。

4.内隐性特征

【教学片段4】摸牌游戏，体会可能性大小。

活动要求：

（1）把4张扑克牌打乱次序后反扣在桌上。每人摸之前组长先把牌混匀，摸出后告诉记录员是什么牌。

（2）根据组长报的花色，画“正”字记录在实验记录卡里，并统计出结果。

（3）按号码次序摸牌，每次摸好后把牌反扣并放于桌面，一共摸30次。

活动后组长汇报摸牌情况，教师根据各组长的汇报将本班情况进行汇总（如图2）。

图2

提问：观察表格，比较摸到红桃和黑桃的次数，你有什么发现？摸牌的结果能说明什么？

小结：在摸牌之前，根据牌的花色，我们可以预计出摸到红桃的次数多，摸到黑桃的次数少。但这并不能代表摸球的结果一定是这样，黑桃牌数虽然少，但因为每一次摸牌的结果不确定，黑桃也有可能被摸到。所以，出现这些结果都是合理的。从这个试验我们也可以看出：事件发生的可能性是有大小的。

通过上述教学环节可以看出，学生的数学活动经验如果仅仅是停留在感性层面是不易被学生把握到的，所以笔者在多次的磨课过程中，让学生通过摸牌游戏自己获得数据，在对数据对比分析的过程中体会可能性的大小，从而让学生的随机意识得以外显。

5.实践性特征

【教学片段5】装球游戏。

活动要求：往口袋里装6个球，要求从中任意摸1个球，可能是绿球。

交流不同的装法（如图3）：

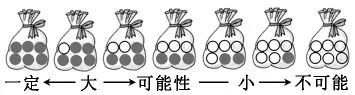
图3

教师小结，同步呈现：“大——可能性——小”。

增加6个球都是绿球的袋子及没有绿球的袋子，引导学生观察不同的装球方法，沟通“一定”“可能”“不可能”之间的关系。

让学生以小组为单位经历“装球游戏”，将活动经验中对于“可能性及可能性大小”的理解投注于解决问题之中，给学生应用的机会，从而在实践过程中将新的活动经验反哺于学生已有的数学活动经验。

二、数学基本活动经验的落实

1.在经历中形成经验

在经历数学活动的过程中，教师需要引导学生在活动的每一个环节中去经历，以形成不同的感受。“可能性大小”一课中，多数学生在实际生活中都对可能性有一些感性认识，具有判断简单随机事件可能性大小的直观经验，这些经验是学生学习这部分内容的基础。在教学中，笔者特别注意激活学生的已有经验，并引导他们将已有经验上升为理性的数学思考。如在讨论“从红桃A、红桃2、红桃3、黑桃4这4张牌中任意摸出1张，是摸出红桃的可能性大，还是摸出黑桃的可能性大”这个问题时，侧重引导学生基于所有可能出现的结果做出合乎逻辑的判断。这些活动都有助于学生将已有的经验“数学化”，从而逐步形成对可能性及其大小的理性认识。

2.在运用中提升经验

要想让学生把在活动中获得的“看不见、摸不着”的经验内化于自身，就需要将整个学习过程中所获得的经验清晰化、条理化。笔者在上述“教学片段5”操作活动之后，帮助学生在交流中逐步澄清“可能性大就是必然，可能性小就是不可能”以及“理论判断与试验结果一定完全一致”等原先模糊的认识，从而使他们更加全面地体验随机现象的特点，提升已有的数学活动经验。

3.在反思中巩固经验

笔者在设计“可能性大小”一课时，紧扣“在具体情境中体验事件发生的随机性”以及“通过试验、游戏等活动，感受随机现象结果发生的可能性是有大小的”这两个基本目标，引导学生主动参与摸球、摸牌、装球等蕴含随机现象的活动。通过多个实践活动的经历，学生初步掌握判断可能性大小的思考方法，感悟随机现象的特点，体验不确定的思维方式。♪