二维PSD的非线性畸变校正算法

王静仪，王兴东，刘 钊，曾 镛,仄士春

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081;2.扬州力德工程技术有限公司，江苏 扬州，225131)

随着制造业的高速发展，自动化焊接在实际工程中的应用越来越广泛，并已成为先进制造技术的重要组成部分。焊缝自动跟踪是焊接自动化的关键技术环节之一，对保证焊缝质量、改善劳动条件、提高生产率有重要的作用。焊缝跟踪系统一般由视觉传感器、控制系统和执行机构三部分组成，其中视觉传感器对整个系统的跟踪精度至关重要。位置敏感探测器 (position sensitive detector, PSD)是一种先进的光电位置传感器，因其分辨率高、响应速度快等优点而被应用于焊缝跟踪[1-2]，但PSD存在的非线性畸变问题会降低焊缝跟踪系统的数据置信度。

为了上述问题，研究人员提出了各种校正方法。袁红星等[3]运用双一次插值及双二次插值算法对PSD的非线性进行补偿，但其精度还有待提高。管炳良等[4]提出了适用于非均匀网格的二维PSD离散标定误差修正方法，经补偿后在PSD中心1 mm范围内示值误差小于2 μm。张风齐等[5]使用双调和样条插值算法来校正PSD产生畸变的离散点，仿真分析显示，校正后在PSD整个感光面上的均方误差不超过2.29 μm。Cui等[6]提出两个线性度指数用于评估二维位置测量精度，并设计了新的估计公式以消除PSD非线性畸变的影响。

本文以二维PSD在焊缝跟踪系统应用中产生的非线性畸变为研究对象，首先对图像缩放算法中应用较多的双三次插值法进行介绍，然后针对PSD在离散标定中出现的非均匀网格提出双三次插值改进算法，最后通过仿真和实验来验证改进算法对于二维PSD非线性畸变校正的有效性以及在实际焊缝跟踪系统中的适用性。

1 二维PSD工作原理

PSD的工作原理是基于半导体的横向光电效应，分为一维和二维两大类，二维PSD可以测量光斑在平面上的运动位置。二维PSD的光敏面常为正方形，有两对电极，其结构原理如图1所示，其中阴影部分为二维PSD的有效工作区域。

当入射光点位置与各电极距离不同时，4个电极收集的电流强度也不相同，并且与光点在光敏面上的位置相对应。光斑中心点的坐标(x,y)可根据下式求得[7]：

(1)

式中：X1、X2、Y1、Y2为每一电极的输出信号(光电流)；L为相邻电极间的距离。

2 PSD非线性畸变校正

制作PSD所用硅片材料的非均匀性往往呈现出一种缓慢的梯度变化。若将整个PSD光敏面上的位置误差函数E(x,y)离散化，得到一系列网格点阵上的误差函数值，对于非网格点上的误差，则可用插值、神经网络等方法进行函数逼近，这样便可得到待校正点的逼近值。

2.1 双三次插值算法

双三次插值是三次插值在二维空间上的一种扩展[8]。为了减少计算复杂度，双三次插值过程被分解为水平和垂直两个一维插值，如图2所示。

图2 双三次插值示意图Fig.2 Schematic diagram of bicubic interpolation

首先进行水平插值，根据待校正点P(x,y)周围4×4点阵的坐标及与待校正点的距离插值，得到4个虚拟点P1、P2、P3、P4；再由这4个虚拟点与待校正点进行垂直插值，得到校正后的点P：

(2)

式中：C1、C2、C3、C4为水平插值系数；H1、H2、H3、H4为垂直插值系数。

针对二维PSD非线性畸变校正，根据式(2)可以整理得出插值函数φ(xp,yq)：

(3)

则点P(x,y)在X、Y方向上的畸变值为：

(4)

式中：EX(xp,yq)和EY(xp,yq)分别为网格顶点(xp,yq)在X、Y方向上的畸变值。

2.2 改进的双三次插值算法

理论上，前述4×4点阵网格是均匀的，以图3中的待校正点P(x,y)为例，按照双三次插值的思想，由式(3)可知，插值函数φ(xp,yq)代表了P(x,y)周围的点对它的补偿，函数值是通过网格中16个点的坐标进行计算的。在均匀点阵中，这16个点的坐标可以由点A1、A2、A3、A4的横坐标和点A1、A5、A9、A13的纵坐标来表示，在计算网格中的任意一点对点P(x,y)的补偿分量时，其实是利用了图3中椭圆圈内7个点的坐标信息。

图3 改进的双三次插值示意图

Fig.3Schematicdiagramofimprovedbicubicinterpolation

然而实际上，PSD自身存在的非线性畸变导致所标定的网格是不等间距的。假如需要求点A7对点P(x,y)的补偿值，根据双三次插值算法，点A7的插值函数φ(xi+2,yj+1)仅与椭圆圈内的点有关。而在非均匀网格中，点A7的横、纵坐标与点A3的横坐标及点A5的纵坐标不相等，因此得到的插值函数φ(xi+2,yj+1)并不准确，无法体现出点A7对点P(x,y)的补偿分量，所以不能笼统地用椭圆圈内的7个点对待校正点的补偿来代替该点所在网格对它的补偿。

下面对双三次插值算法进行改进，仍以点A7为例进行说明。A7对待校正点P(x,y)的补偿分量应该与两点之间的距离相关，即距离越近补偿分量越大。将网格中与A7位于同一行或同一列的7个点(A3,A5,A6,A7,A8,A11,A15)的坐标值代入式(3)中得到插值函数φ(xi+2,yj+1)，这样就反映了A7点对P(x,y)的补偿分量，也反映了两点之间的距离关系。其他点对P(x,y)的补偿分量同样按照上述方法得到，此处不赘述。最后通过式(4)即可得出点P(x,y)最终的校正值。

基于改进双三次插值的PSD非线性畸变校正算法流程如下：

(1)在PSD光敏面上得到均匀点阵Ai，并计算出点阵中每个点在X、Y方向的畸变值；

(2)找到某待校正点P(x,y)在Ai中所处4×4网格；

(3)得到网格中每个顶点所在行和列的7个点的坐标，代入式(3)，求得插值函数φ(xp,yq)；

(4)将φ(xp,yq)和该顶点的畸变值代入式(4)，得出待校正点P(x,y)在X、Y方向上的畸变值EX(x,y)和EY(x,y)；

(5)EX(x,y)和EY(x,y)分别加上点P(x,y)的横、纵坐标即为校正后的P点坐标。

3 算法验证

3.1 仿真

仿真采用的数据由PSD的畸变模型[9]得到：

(5)

式中：I1～I4为4个电极输出的电流；I0为光生电流；X、Y分别为光点的理论横、纵坐标；l为PSD光敏面的边长，这里取单位长度1。

根据式(5)以及二维PSD的位置计算公式(1)，产生9×9的样本点集(见图4)，得到每个点的实际坐标和测量坐标。分别用双一次插值[3]、双二次插值[3]、改进的双二次插值[4]、双三次插值以及本文提出的改进双三次插值算法对图4所示非线性畸变进行校正，计算出各个算法的误差均差和方差，如表1所示。

图4 样本点集Fig.4 Sample points

表1各算法的校正误差对比

Table1Comparisonofcorrectionerrorsbydifferentalgorithms

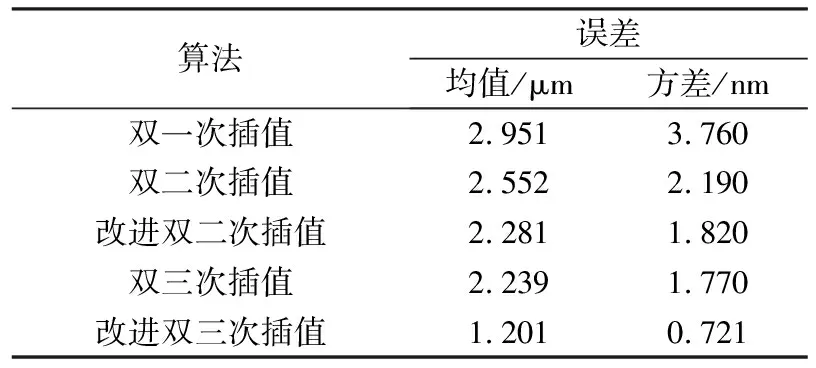
算法误差均值/μm方差/nm双一次插值2.9513.760双二次插值2.5522.190改进双二次插值2.2811.820双三次插值2.2391.770改进双三次插值1.2010.721

由仿真结果可得，与其它4个算法相比，改进双三次插值算法的误差均差和方差都有明显降低，表明该算法能够很好地实现PSD的非线性畸变校正。

3.2 实验

实验装置如图5所示。选用深圳达瑞鑫光电科技有限公司生产的PSD-1515型位移传感器，其最大感光面积为15 mm×15 mm，分辨率为1 μm，光谱响应范围为380～1100 nm；点激光器的功率为50 mW、波长为650 nm；三轴精密位移平台的精度为1 μm。PSD的有效工作区域在光敏面中心8 mm×8 mm范围内，故本实验仅在此区域内进行畸变校正。

图5 实验装置Fig.5 Experimental apparatus

实验步骤如下：

(1)系统初始化。将PSD固定于三轴精密位移平台上，使点激光垂直照射于PSD的感光区域，调整激光器焦距，使光斑面积最小。

(2)获取误差函数。选择一定步长S0，由于PSD的原点存在偏移，故设计螺旋轨迹，控制精密位移平台，使激光点从原点开始分别沿PSD的X、Y方向移动，获得一系列网格点阵(xi,yi)，根据式(6)可以得到每个顶点的误差值:

(6)

式中：xi、yi为理论坐标值；xi0、yi0为PSD测量值。

(3)激光点回到原点位置，重复步骤(1)进行初始化。

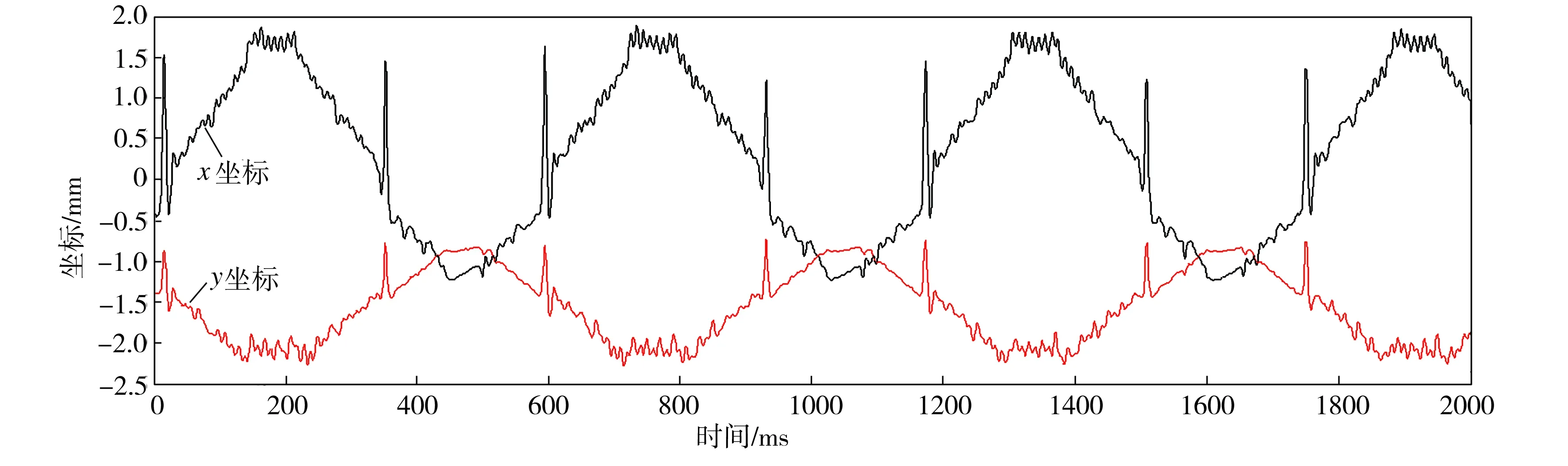
(4)修正待校正点。选择步长S1(S1

表2是本文算法对PSD非线性畸变的部分校正结果，其中，样本1～5是PSD光敏面中心1 mm×1 mm范围内(A区)的采样点，样本6～10是PSD光敏面中心1 mm×1 mm以外、8 mm×8 mm以内范围(B区)的采样点。由实验结果可知，对A区样本点的校正效果较好，全体样本的平均误差为4 μm；对B区样本点的平均校正误差为16 μm；越靠近PSD有效区域中心，误差越小。

表2 改进算法对PSD非线性畸变校正的部分实验结果Table 2 Partial experimental results of PSD nonlinear distortion corrected by the improved algorithm

上述实验是对静态光斑的采集与畸变校正，而在实际焊缝跟踪系统中，PSD采集的是动态变化的光斑。为了验证本文算法的实用性，采用点激光器在待焊板材上产生动态光斑，通过二维PSD进行跟踪。如图6所示坐标-时间曲线为系统采集的未经过校正的原始数据，其中x、y分别是动态光斑通过PSD示出的横、纵坐标。将原始数据通过改进的双三次插值算法进行校正，校正前后的数据与理论值的误差分布如图7所示，经过计算得出原始数据的误差均值为37.5μm，校正后的误差均值为6.2 μm。由此可见，改进的双三次插值算法可以应用于焊缝跟踪系统中的PSD非线性畸变校正。

图6 校正前的焊缝数据Fig.6 Weld seam data before correction

图7 校正前后的误差分布Fig.7 Error distributions before and after correction

4 结语

本文在分析双三次插值算法原理的基础上，提出了适用于PSD非线性畸变校正的改进双三次插值算法，然后通过仿真和实验进行算法验证。采用改进算法对PSD非线性畸变的仿真样本数据集进行校正后，在PSD全感光面上的误差均值为1.2 μm，与其它4种经典插值算法相比有明显优势。实验结果显示，经过本文算法校正，PSD光敏面中心1 mm×1 mm范围内的非线性畸变误差平均值为4 μm，1 mm×1 mm以外、8 mm×8 mm以内范围的误差平均值为16 μm。该算法对于PSD采集的动态光斑也取得了比较好的校正效果，可实际应用于焊缝跟踪系统。