基于深度置信网络和信息融合技术的轴承故障诊断

蒋黎明，李友荣，徐增丙,2，鲁光涛

(1.武汉科技大学冶金装备及其控制教育部重点实验室，湖北 武汉，430081；2.华中科技大学数字制造设备与技术国家重点实验室，湖北 武汉，430074)

滚动轴承是旋转机械中最常见和最关键的零部件之一，及时准确地掌握其故障损伤情况，对保障机械设备安全运行、避免经济损失和灾难性事故具有重要的意义。故障诊断的本质就是模式识别，而深度学习作为机器学习研究中的一个新领域，近年来已成功应用于计算机视觉[1]、语音识别[2]等模式识别领域。与一般的神经网络和机器学习模型相比，深度学习可以更精确、高效地解决复杂问题[3]。深度置信网络(deep belief network，DBN)是最具代表性的深度学习技术之一，在故障诊断中的应用越来越多。Tamilselvan等[4]提出一种基于DBN的多传感器故障诊断方法，并运用于飞机发动机和电力变压器的故障诊断。Chen等[5]将稀疏自动编码机(SAE)和DBN相结合进行轴承故障诊断，先从不同传感器振动信号中提取15种时域特征和3种频域特征，输入到SAE中进行特征融合，再利用得到的融合特征向量训练DBN。陶洁等[6]提出基于Teager能量算子(TEO)和DBN的滚动轴承故障诊断方法，用TEO提取滚动轴承振动信号中的瞬时能量，输入到采用层次优化算法调整参数后的DBN模型中进行故障识别。张淑清等[7]提出基于双树复小波(DTCWT)和DBN的轴承故障诊断新方法，先用DTCWT将信号分解，进而提取能量熵作为故障特征，采用DBN小样本模型对故障进行分类。

虽然DBN已经广泛应用于故障诊断领域，但仍然存在以下两方面问题：①大多数研究仅将DBN作为一个分类器，且需要人工提取故障特征参数作为DBN的输入，因此未能充分利用DBN的特征提取能力；②利用DBN网络模型对信号进行表征分析时易忽略局部信息，从而导致故障识别率不高、诊断系统可靠性差等问题。

为此，本文提出一种基于深度置信网络和信息融合技术的滚动轴承故障识别方法。首先采用集合经验模式分解(EEMD)方法将单一传感器采集的轴承振动时域信号分解为若干个固有模态函数(IMF)，并分别作为各DBN的输入，然后采用投票表决法将每个DBN识别的结果进行信息融合，从而获取最终的故障诊断结果。

1 基于DBN和信息融合技术的故障识别方法

1.1 方法概述

考虑到采用传统DBN方法进行诊断分析时主要是针对信号的全局信息，而未能充分利用其局部信息特征，因此本文建立基于DBN和信息融合技术的故障诊断模型，其故障识别过程如图1所示。

图1 故障识别过程Fig.1 Process of fault recognition

具体步骤如下：

(1)获取滚动轴承的故障振动信号，对其进行EEMD分解得到若干IMF。

(2)选取前n个IMF，分别作为n个DBN的输入。

(3)设定DBN中隐藏层数N和学习率ε，并以无监督学习的方式逐层训练；再利用反向传播神经网络(BPNN)的误差反向传播原则进行权值和偏置的微调。

(4)将n个DBN的识别结果采用投票法进行处理，得到信息融合后的故障诊断结果。

1.2 采用EEMD的信号处理

经验模式分解(EMD)是针对非线性信号的时频信号分析方法，可以自适应分解数据并获得一系列IMF。EMD算法非常适合于分析具有非平稳特性的滚动轴承振动信号。然而在实际应用中发现，EMD分解过程中存在模式混合的问题[8]，也就是说，一个IMF中包含不同的频率分量，或者相同的频率分量被分解为不同的IMF。为了解决这一问题，研究人员又提出了EEMD算法[9]，该算法的核心是先通过引入具有频率均匀分布特性的高斯白噪声来抑制模态混频的出现，再利用EMD方法对原始信号进行重复分解，将原始振动数据分解为一系列具有不同尺度和连续特性的IMF。

1.3 DBN的基本构架和训练过程

1.3.1 DBN的基本构架

DBN是由多层受限玻尔兹曼机(RBM)和BPNN构成的深层神经网络，图2所示为一个由3个RBM堆叠而成的DBN网络结构模型。多层体系结构确保DBN可以通过自下而上的学习方式在RBM序列中进行训练，并通过BPNN进行自上而下的后向微调学习[10]。

若被害人与犯罪嫌疑人、被告人关系正常或素不相识，则存在虚假陈述的可能性较小。但若被害人与犯罪嫌疑人或被告人关系不睦或素有仇怨，则有捏造或夸大犯罪事实的可能性，则此时更应尽力查找是否存在与被害人陈述事实相矛盾的事实或证据，对被害人陈述进行仔细的审查判断。例如：若被害人陈述与被告人此时出示的证据存在矛盾时，不应轻信被害人陈述而带着有色眼镜去看待犯罪嫌疑人、被告人的供述与辩解。此时应运用证伪思维首先对被害人陈述进行审查，若能找出被害人陈述的一两个矛盾之处，则此时应首先搜集关于犯罪嫌疑人、被告人无罪或罪轻的证据以免造成冤假错案或轻罪重判的情况发生。

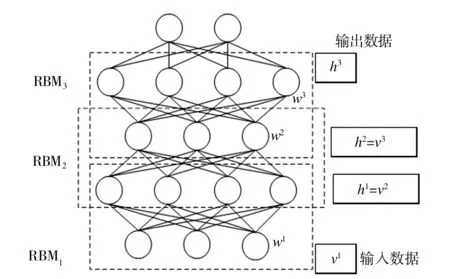
图2 DBN结构示意图Fig.2 Structural diagram of DBN

RBM由两层网络组成，即可见层(v)和隐藏层(h)，可见层和隐藏层之间通过权值w连接，层内之间相互独立无连接。在DBN中，输入数据经过底层RBM学习后，底层RBM的隐藏层成为下一个RBM的可见层，依次逐层传递。DBN通过堆叠RBM建立了逐层贪婪学习的连续层次结构[11]。

在RBM中，可见单元和隐藏单元分别用vi和hj表示。可见单元vi和隐藏单元hj之间连接的权重用wij表示。ci表示可见单元vi的偏置，bj表示隐藏单元hj的偏置。所有RBM的参数bj、ci和wij构成DBN中的数据集θ。DBN的能量函数为：

(1)

DBN训练的最终目的是寻找最佳参数θ，以最小化模型能量误差并使模型处于平衡状态。因此，利用能量函数来定义v和h之间的联合概率分布如下：

(2)

由于DBN层内无连接，可见节点和隐藏节点的条件概率分布可通过下式计算：

(3)

(4)

1.3.2 DBN的训练过程

一般来说，DBN训练过程包括两部分：预训练和微调。

(1)预训练是一种无监督的学习过程，它使用未标记的数据来训练单个RBM。DBN可以通过自下而上的学习方式在RBM序列中进行训练，可从原始的信号数据中提取到较为抽象和高层次的表达。在预训练中，RBM中的权重和阈值被持续更新，直到最大迭代次数，关于RBM 网络的更新规则参见文献[12]。

(2)微调是一种监督学习过程，它利用反向传播进一步降低训练误差，提高DBN的分类精度。由于BPNN是监督学习，因此微调使用标签数据进行DBN训练。与DBN中的无监督训练一次仅处理一个RBM不同，BPNN同时训练DBN中的所有层。通过模型输出和标签数据来计算BPNN的训练误差。反向传播学习持续进行，经过多次调整即可达到整个DBN最优。

1.4 基于简单投票法的信息融合

最直接的信息融合方法是简单投票法(simple voting)，也称为多数投票法(majority voting)[13]。如同选举投票一样，分为被选举者和选举者。投票规则是，每一选举者都为确定的被选举者投上一票且仅此一票，得票最多的被选举者胜出。

2 应用实例分析

2.1 实验数据

为了验证本文方法的有效性，采用美国凯斯西储大学电气工程实验室提供的滚动轴承振动信号数据进行分析(http://www.eecs.case.edu/laboratory/bearing/download.htm)。实验装置主要包括1.47 kW电机、扭矩传感器、测力器、电气控制等部件。实验轴承为SKF公司生产的6205-2RS深沟球轴承，轴承安装在电机的驱动端，轴承振动信号在3种不同大小的负载下采集得到，采样频率为12 kHz。

实验系统模拟了轴承的正常工作状态以及发生外圈故障、内圈故障和滚动体故障时的工作状态，并且每种故障类型都有3种损伤程度。用N表示轴承正常状态；用IR1、IR2和IR3分别表示滚动轴承内圈轻、中、重度损伤，对应于内圈损伤点直径为0.18、0.36、0.53 mm。依此类推，OR1、OR2和OR3分别表示滚动轴承外圈轻、中、重度损伤状态；BE1、BE2和BE3分别表示滚动体轻、中、重度损伤状态。

根据0～1.47 kW区间3种负载下的实验数据，分别构造数据集A、B和C，每个数据集均包含轴承正常状态和9种故障类别。每个时域样本的采样点数为500，每种状态类别可以得到200个样本。考虑实际情况，每一种故障可能会对应多种负载，因此综合数据集A、B和C，得到数据集D，其包含600个样本。

2.2 轴承振动信号分解

EEMD算法中有两个重要参数，分别为白噪声的幅值k和总体平均次数M，参照文献[9],取k=0.1，M=100。以滚动轴承在IR1故障状态下的原始时域信号为例，经EEMD处理后得到若干IMF分量，其中前10个如图3所示。

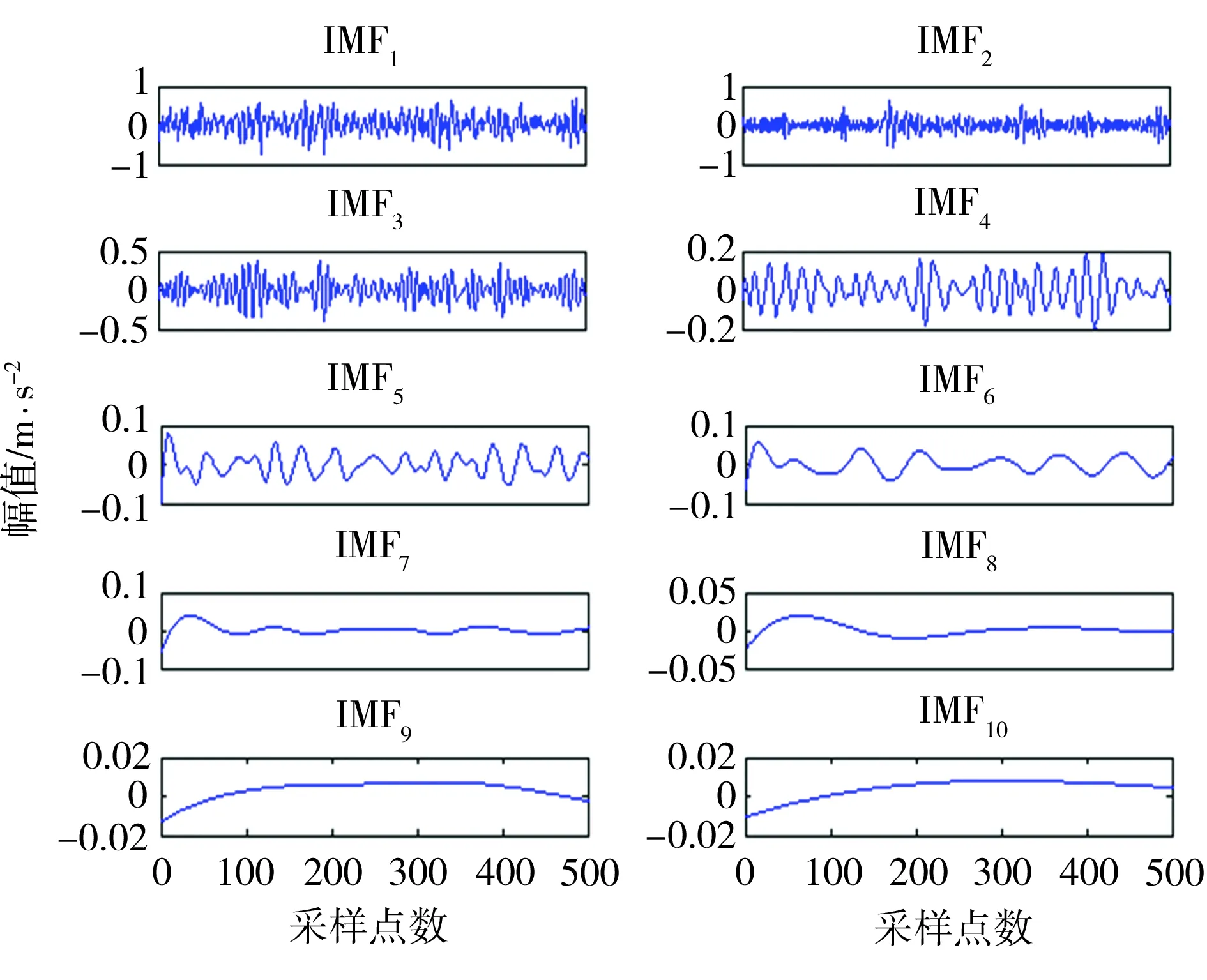
图3 IR1故障振动信号的EEMD分解Fig.3 EEMD decomposition of IR1 fault vibration signals

2.3 故障诊断结果与分析

由于通过EEMD得到的IMF中存在对故障不敏感的分量，本文选取前t个IMF分别作为输入数据带入DBN，得到t个DBN识别结果，再将这t个识别结果通过简单投票法处理，得出信息融合后的故障诊断结果。对于DBN结构参数的选取，目前尚无成熟理论，理论上来说，隐藏层的网络层数和节点数越多就越容易挖掘出原始数据特征，但同时又会出现过拟合问题，计算成本也会增加[14]。本文中DBN模型采用经典的4层结构，各层节点数分别为500、100、100、10，学习率ε=0.0001，最终结果取10次实验所得的平均值。随机选取每个故障类别样本的60%为训练样本，剩余作为测试样本。

由于篇幅所限，本文仅给出针对单负载数据集A和多负载数据集D的分析结果。对于单负载数据集，DBN的迭代次数设为3000；对于多负载数据集，DBN的迭代次数设为6000；其余参数均相同。故障识别结果如图4和图5所示，其中柱状图表示第t个IMF单独输入DBN后的识别率，折线图表示前t个IMF输入t个DBN后，将t个识别结果信息融合后的最终识别率。

从图4、图5可见，原始振动单负载数据集A和多负载数据集D经EEMD分解后得到不同频率段的IMF，将它们分别作为DBN输入数据进行故障状态识别的准确率除个别数据外均低于87%。但运用简单投票法将前t个DBN识别的结果进行信息融合后，识别率随着t的增加而不断提高，并且当t=10时单负载和多负载下的故障状态识别率分别达到100%和98.08%。因此本文提出的故障识别模型不仅可以在单一负载条件下进行高精度识别，也能够在多种负载共存时进行故障提取与识别。

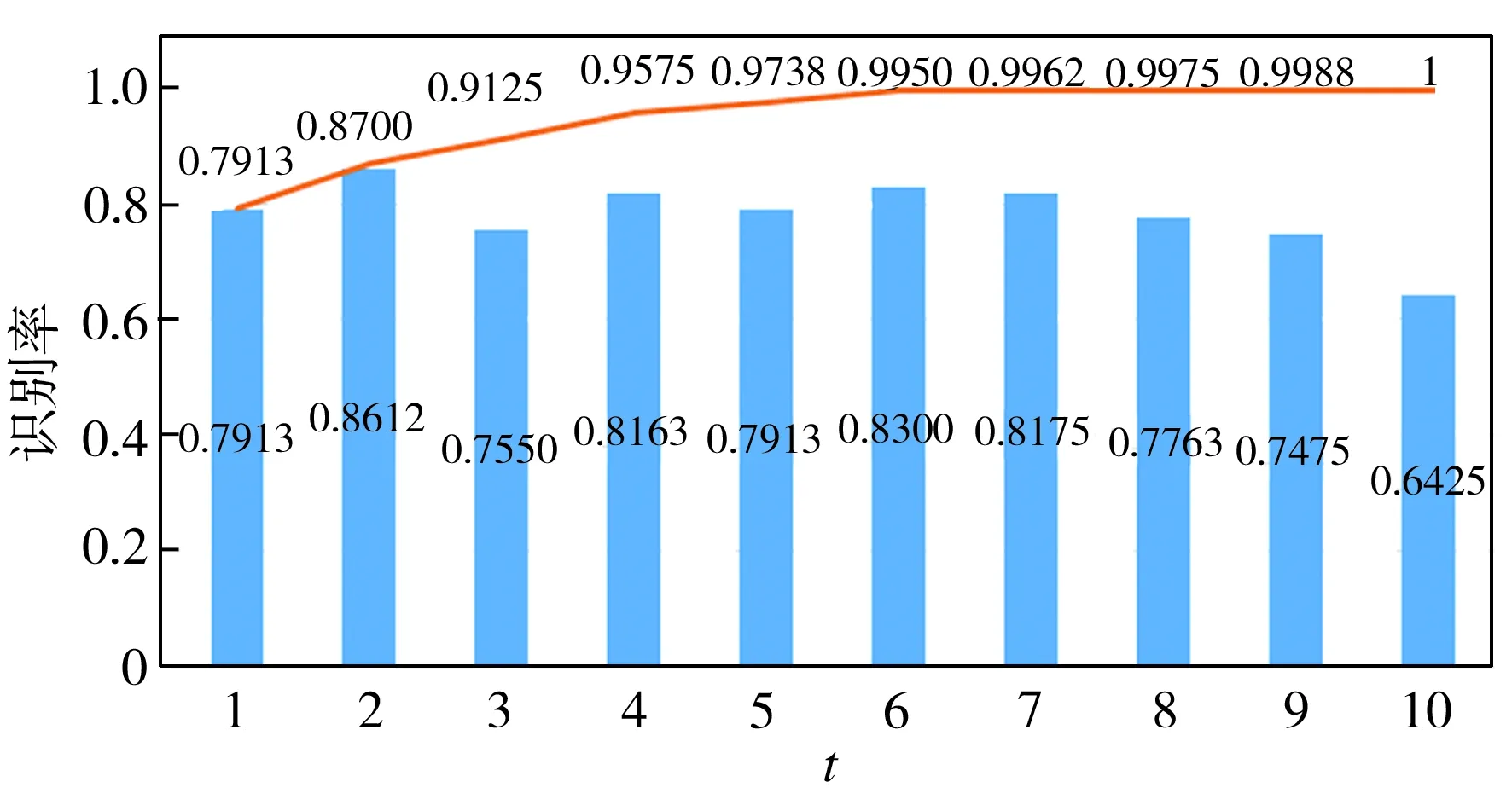
图4 数据集A的识别结果Fig.4 Recognition results of Dataset A

图5 数据集D的识别结果Fig.5 Recognition results of Dataset D

为了进一步评估本文方法对轴承故障的识别能力，将其与传统DBN故障诊断方法和文献[6]提出的TEO-DBN故障诊断方法进行对比，结果如表1和表2所示。由表1可见，与TEO-DBN方法相比，本文方法不需要任何特征提取过程，直接将振动时域信号作为DBN的输入，在单负载时的故障识别率更高。结合表1和表2可知，与未进行信息融合的传统DBN方法相比，本文方法不仅在单负载条件下故障识别率较高，而且针对更接近实际工况的多负载情况进行测试时获得高达98.08%的平均故障识别率，充分验证了该方法在轴承故障诊断中的有效性和精确性。

表1不同数据集的识别结果对比

Table1Comparisonofrecognitionresultsofdifferentdatasets

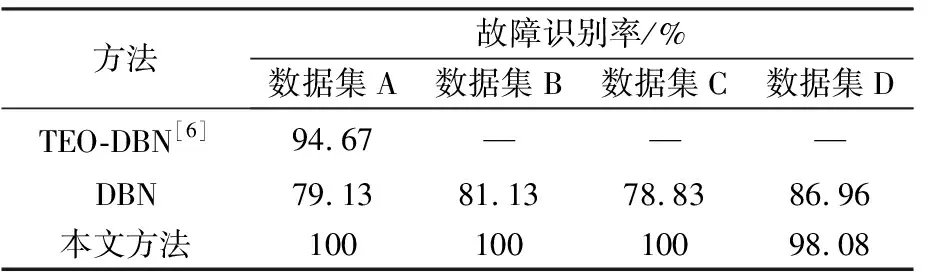
方法故障识别率/%数据集A数据集B数据集C数据集DTEO-DBN[6]94.67———DBN79.1381.1378.8386.96本文方法10010010098.08

表2多负载下不同故障类别的识别结果对比

Table2Comparisonofrecognitionresultsofdifferentfaultcategoriesundermulti-loadconditon

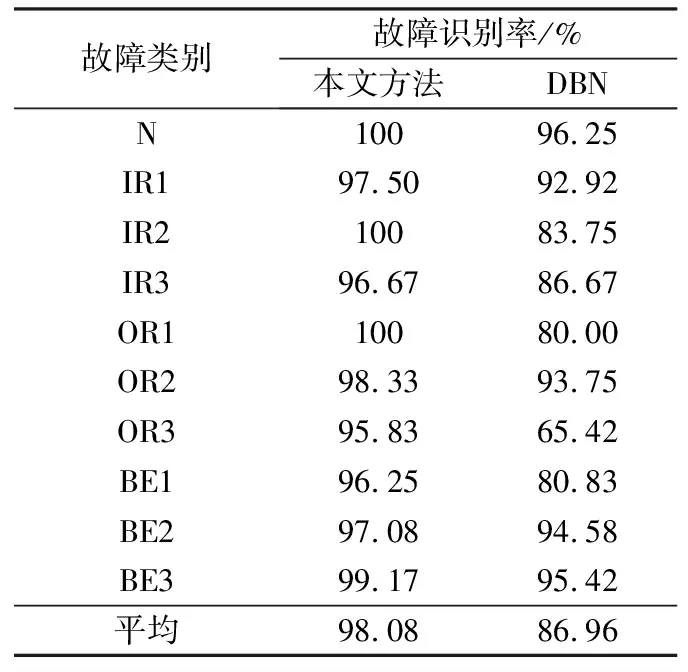
故障类别故障识别率/%本文方法DBNN10096.25IR197.5092.92IR210083.75IR396.6786.67OR110080.00OR298.3393.75OR395.8365.42BE196.2580.83BE297.0894.58BE399.1795.42平均98.0886.96

3 结语

本文提出一种基于DBN和信息融合技术的轴承故障诊断新方法，其将原始滚动轴承振动时域信号进行EEMD分解，得到多个IMF，分别作为DBN的输入，再将多个DBN的识别结果进行信息融合。通过对单负载和多负载下轴承故障状态的识别证明了该方法的有效性。本文方法的优点在于：①能从IMF中逐层提取信号特征，不需要提取时域或频域特征；②运用多个DBN网络模型,可充分发挥DBN特征提取的能力，获得较高的故障识别率；③不仅适用于轴承的单负载工况，也适用于接近工程实际的多负载工况。