基于能量变分法的曲线组合箱梁畸变效应分析

陈百玲，马前程，朱耀斌，王连广

(东北大学资源与土木工程学院，辽宁 沈阳 110819)

钢与混凝土组合箱梁是通过剪力键将钢箱梁和混凝土板连接在一起的新式梁，其承载力强、抗扭刚度大、重量轻，具有很大的应用前景[1]。学术界对组合箱梁的剪力滞、扭转、界面滑移[2-4]等效应进行了研究。此外，还应重视其横截面在荷载作用下发生的畸变[5]。

当箱梁壁厚较薄，隔板较少时，会有较大的周边变形，畸变效应不容忽略[6]。起初，畸变的研究主要关注同种材料的箱梁，研究方法多样。张元海等[7]应用了能量变分法推导并验证了同种材料的薄壁箱梁的畸变计算公式。J.Lee[8]应用弹性地基梁法(BEF法)，探究了钢箱梁长径比和隔板数目对畸变效应的影响。REN Yangzhi等[9-10]考虑了剪切应变影响下，悬臂钢箱梁的隔板数目和厚度对畸变效应的影响，并通过试验和有限元对比，证明了初始参数法适用于钢箱梁畸变分析。C.H.Yoo[11]采用BEF法，分析了曲线单箱和曲线分离式多箱梁的应力分布特点，为装配式钢箱梁桥的设计提供了参考。M.Arici[12]应用适用性强的哈密顿结构分析法，分析变截面和变曲率箱梁桥的畸变效应特点，克服以往仅对单一截面研究的缺陷，更加符合实际要求。N.I.Tsiptsis[13]通过相似方程法，减少了静力和曲率耦合作用引起的分析误差，使曲线钢箱梁的畸变计算更加精确。

组合箱梁的畸变效应是基于钢箱梁的研究。组合梁在施工过程中，截面性质的不连续，此时的畸变效应与成桥后有很大不同，为防止组合梁变形过早，要对施工阶段的受力情况进行单独考虑[14]。针对施工荷载，朱颖杰[15]对不同支撑条件下的开口组合梁畸变效应进行研究，对施工阶段的畸变计算进行了修正。S.J.Fatemi等[16]、Z.Kolakowski等[17]研究了组合箱梁在集中荷载和扭转作用下的应力分布规律。ZHU Yingjie[18]发现增加隔板数目和隔板刚度可迅速减小组合梁畸变，但隔板数目和刚度存在合适范围，过多的隔板和过大的刚度对控制畸变作用不大。LI Lifeng[19]和韩国顺[20]分别使用初参数法和试验法，对波纹钢腹板组合梁畸变效应进行研究。ZHU Li[21]通过试验，研究了曲线组合梁剪力键数目对畸变效应的影响。冯康平[22]等对弯扭组合作用下的曲线组合箱梁进行分析，得出了高跨比和隔板对畸变的影响。

针对箱梁畸变效应，大多研究仅针对同一种材料。对于不同材料的组合箱梁研究较少，且研究大多关注横隔板，而其他几何参数的影响研究不足。基于此，笔者通过能量变分法建立曲线组合箱梁畸变方程，分析集中荷载作用下，组合梁顶板厚、腹板厚、梁高、底板宽及曲率半径对箱梁畸变效应的影响。研究表明：增大组合箱梁的曲率半径可显著减小其畸变角；不同线形的曲线组合箱梁，畸变的控制要点不同；增加组合箱梁的梁高和钢腹板的厚度可以显著减小畸变效应；混凝土顶板对控制组合箱梁畸变贡献很小，顶板厚引起的畸变角变化可以忽略；随着曲率半径增加，底板宽度对畸变的影响逐渐减小；在控制结构畸变变形方面，梯形截面优于矩形截面。

1 畸变方程

依据箱形曲线组合梁截面形式以及受力特点，在不影响分析结果的前提下，采用下列基本假定:各板为各向同性，曲率相同且符合平截面假定;箱壁为薄壁钢板，壁厚方向应力无变化;不考虑界面滑移及连接件变形对梁畸变的影响。

组合箱梁截面具体尺寸见图1所示。图中，tc为混凝土板厚；b4为顶板宽；b5为翼缘板宽；ts1为钢腹板厚；ts2为钢底板厚；O为截面形心。

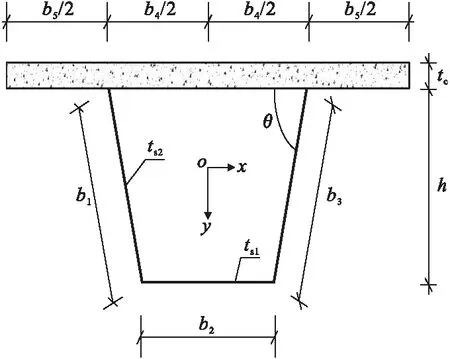
图1 截面尺寸

1.1 畸变框架应变能

薄壁理论[23]认为箱梁畸变由框架应变能和翘曲应变能组成。当截面产生畸变角γ时，会对框架体系产生影响，使框架的角点处出现水平位移，位移值为γb1sinθ。此时，框架所需的应变能与框架发生γb1sinθ位移能量相同。框架横向变形和弯矩见图2和图3所示。

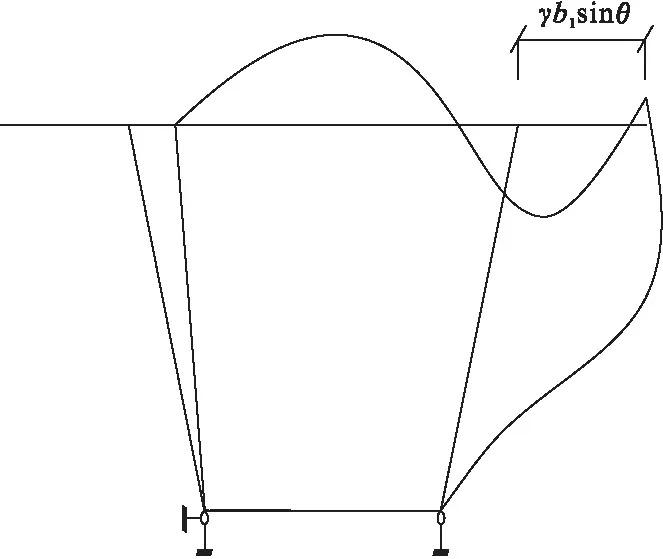
图2 框架横向变形图

图3 框架弯矩图

由图3可知:

(1)

式中:γ为畸变角；K1、K2为系数。

将顶板中间断开，在开口处设置垂直于顶板未知力X1，作为基本体系。当顶板发生大小为γb1sinθ的水平位移时，用力法对半结构进行计算，此位移对应的水平荷载P:

(2)

(3)

[3b1b2(b2+b4)+b1(b2-b4)(2b2+b4)].

(4)

得出系数K1和K2:

(5)

(6)

畸变框架应变能:

(7)

其中，W1为框架横向刚度。

(8)

1.2 畸变翘曲应变能

组合梁各板的畸变翘曲应力见图4。

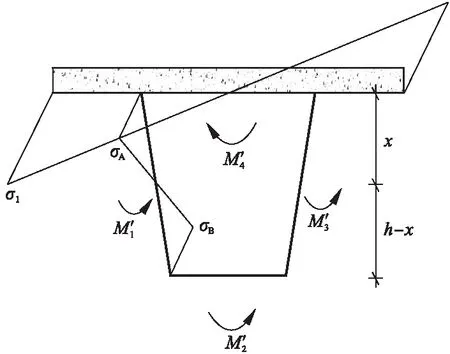
图4 畸变翘曲应力图

根据应力平衡，设畸变翘曲系数:

(9)

翘曲正应力与各板扭矩关系:

(10)

(11)

(12)

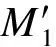
由变形计算公式，得出各板在平面内的挠度:

(13)

(14)

(15)

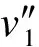
通过求导，可得到挠度与畸变角之间的关系[23]:

(16)

式中:γ″为畸变角函数的二阶导。

将式(13)～式(16)联立，由各板间变形关系，可得出畸变角与畸变翘曲正应力的关系:

(17)

(18)

顶板:

(19)

底板:

(20)

腹板:

(21)

对各板的翘曲应变能进行积分后，求得该梁段畸变翘曲应变能:

(22)

其中，W2为截面翘曲惯性矩。

(23)

1.3 荷载势能

扭矩产生的荷载势能:

(24)

藕联效应产生的荷载势能:

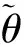
(25)

式中:R为曲率半径;Mx为箱梁纵向弯矩，近似按照直线简支梁计算。

1.4 畸变微分方程

箱梁总势能:

Π=U1+U2+V1+V2.

(26)

根据最小势能原理[23]，求出畸变微分方程:

(27)

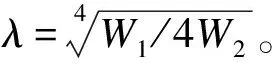
畸变双力矩:

B=-W2γ″.

(28)

2 算例分析

以简支组合箱梁为例，跨径30 m，曲率半径50 m，Es=2.0×105MPa，Ec=3.5×104MPa，截面尺寸如图5所示。在箱梁跨中处，顶板中央位置作用向下的集中荷载500 kN。

图5 组合箱梁截面尺寸

使用弹性地基梁法[8,11]，以跨中截面为坐标原点，以初参数法求得式(27)、式(28)的通解:

(29)

(30)

结合畸变荷载函数，得跨中截面的畸变角γA及双力矩BA计算公式:

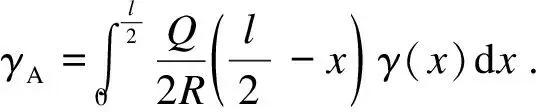
(31)

(32)

式中:Q为集中荷载。

根据组合梁几何参数和材料特性，得出:W1=4.70×106N·m4，W2=7.51×109N·m4，λ=0.111。将边界条件γl/2=0，Bl/2=0代入式(29)～式(30)，得γA=0.008 rad，BA=5.70×105N·m2。

3 参数分析

以算例中的截面尺寸、边界条件、荷载形式为基础，根据式(31)和式(32)，改变设计参数，得出不同曲率半径下组合梁的畸变角，以反映此设计参数对畸变效应的影响。

3.1 梁高的影响

改变梁高，畸变角变化规律如图6所示。

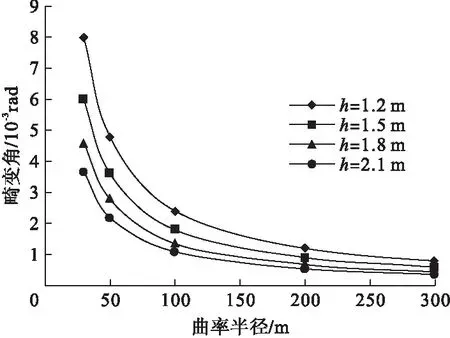
图6 畸变角随梁高的变化规律

由图6可知，梁高增加时，箱梁的畸变角逐渐减小。在曲率半径小于100 m的情况下，随着梁高增长，畸变角迅速减小。在曲率半径大于100 m以后，曲线极差变化趋势减缓，增加梁高对畸变角的影响逐渐降低。当梁高为1.8 m，高跨比为0.6时，增加梁高对减小畸变效果减弱。曲率半径为100 m时，梁高由1.2 m增加到2.1 m时，畸变角减小54.2%。当曲率半径为300 m，梁高由1.2 m增加到2.1 m时，畸变角减小约50%。可见，增加梁高显著减少截面畸变效应，在工程中应采取适当的梁高。

3.2 混凝土板厚的影响

改变组合梁混凝土板厚，畸变角变化情况如图7所示。

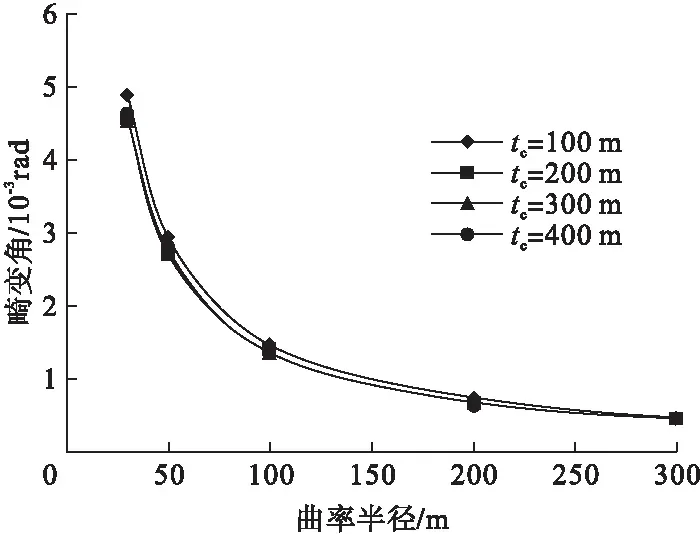
图7 畸变角随混凝土板厚的变化规律

由图7可知，随着混凝土板厚的增加，同一曲率半径下各曲线的畸变角数值几乎重合，增大板厚对减小畸变角无明显效果。在5种曲率半径下，组合箱梁混凝土板厚度由100 mm提高至400 mm时，畸变角平均降低了8.2%，且5种情况下，不同顶板厚的组合梁畸变角相差均未超过10%。这是由于混凝土板厚对组合箱梁刚度影响较小，所以对控制箱梁畸变效应贡献较小。

3.3 钢腹板厚的影响

改变组合梁钢腹板厚，畸变角变化情况见图8所示。

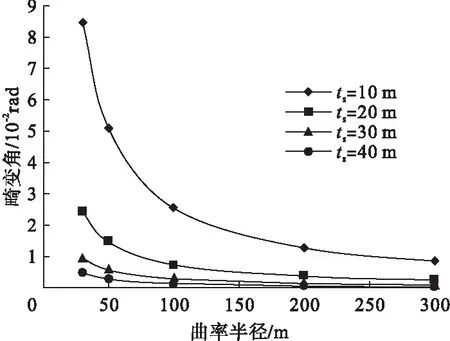
图8 畸变角随钢腹板厚的变化规律

由图8可知，当钢腹板的厚度增加时，箱梁的畸变效应明显减小。在箱梁的曲率半径为50 m的情况下，钢腹板厚度由10 mm增加至30 mm时，畸变角减小了71.2%。当钢腹板厚度为10 mm时，即使增大曲率半径至300 m，箱梁畸变角仍大于0.01 rad，远超其他厚度下的结果。当钢腹板厚增加至30 mm时，畸变角大幅度减小，如继续增加钢腹板厚，畸变角曲线十分接近。因此，在进行箱梁设计时，钢腹板厚度不宜小于20 mm，且厚度存在合适的范围。

3.4 底板宽度的影响

底板宽度改变后，组合梁畸变角变化情况如图9所示。

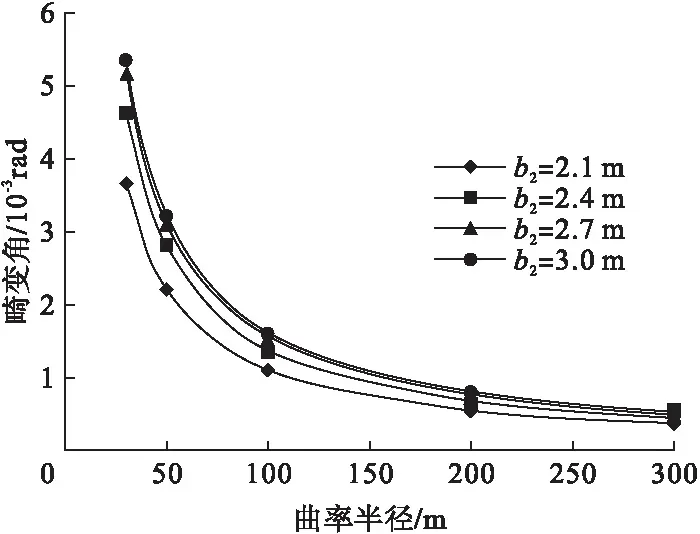
图9 畸变角随底板宽度的变化规律

由图9可知，当底部钢板宽度减少时，箱梁的畸变效应也相应减小。在曲率半径为50 m的情况下，底板宽2.1 m的组合梁所产生的畸变角，仅为底板宽3 m的组合梁畸变角的68.8%。在曲率半径大于100 m后，不同底板宽度的组合梁畸变角十分相近，可知当曲率半径较大时，底板宽度不再是控制畸变的主要因素。

增加底板宽度后，截面趋近于矩形，此时矩形截面与其他梯形截面相比，畸变角前者均大于后者，证明选择梯形的截面形状更有利于限制结构的畸变，且宽高比宜接近1。

3.5 综合分析

图6～图9中，不同曲率半径下，改变梁高、板厚等设计参数后，产生的畸变角最大值与最小值做差，得到极差。通过极差的大小，反映4种设计参数对控制畸变效应的敏感性，某项设计参数的极差越大，畸变效应影响越大，极差结果见表1。

表1 设计参数引起的畸变角极差

由表1可知，在不同曲率情况下，改变钢腹板厚度产生的畸变角极差最大。由此，除曲率半径以外，应最为注重钢腹板厚。在曲率半径较小时，梁高也是降低畸变的有效手段，但随着曲率半径增加，极差逐渐减小。

混凝土顶板厚引起的极差始终较小，数量级远小于其他参数。对比钢腹板厚和混凝土顶板厚引起的畸变角极差总和，前者约为后者的20倍。

底板宽度在曲率半径小于50 m时，底板宽度引起的畸变角极差较大。与梁高类似，随着曲率半径的增长，底板宽度对整体畸变的影响逐渐减小。

4 结 论

(1)增大组合箱梁的曲率半径可显著减小其畸变角；为了避免结构出现过大的畸变效应，在工程中组合箱梁的曲率半径不宜小于100 m；不同线形的曲线组合箱梁，畸变的控制要点不同；曲率半径小于100 m时，控制组合箱梁畸变要关注梁高、底板宽和钢腹板厚，高跨比宜大于0.6，高宽比宜接近1，钢腹板厚宜大于30 mm;当曲率半径大于100 m时，控制组合箱梁畸变主要关注钢腹板厚，腹板厚宜为20～40 mm。

(2)增加组合箱梁的梁高和钢腹板的厚度可以显著减小畸变效应；曲率半径为50 m时，当梁高从1.2 m增至2.1 m时，组合梁的畸变角减小了54.2%;当钢腹板厚度从10 mm增至20 mm时，组合箱梁的畸变角减小了71.2%。

(3)混凝土顶板对控制组合箱梁畸变贡献很小，顶板厚引起的畸变角变化可以忽略；随着曲率半径增加，底板宽度对畸变的影响逐渐减小；在控制结构畸变变形方面，梯形截面优于矩形截面。