基于条纹分析技术的镜头畸变校正实验设计

吴杰鸿， 翁嘉文， 曾应新

（华南农业大学电子工程学院（人工智能学院），广州 510642）

0 引言

光学条纹分析技术［1-3］是光学信息处理的核心技术之一，也是高校光信息专业教学的核心内容之一。该技术在光学元件检测［4］、光学三维传感［5］以及全息干涉检测等分析［6］中均有广泛的应用。针对现今被广泛运用于计算机视觉、车载交通、大场景观测、军事和医疗监控成像系统等领域［7-10］的宽视场成像特性广角镜头所存在的畸变问题［11］，设计了一套基于光学条纹分析技术的镜头畸变校正实验检测与分析系统，开拓了光学条纹分析技术的拓展应用教学。该系统通过数值模拟展现镜头畸变校正的条纹分析过程，包括对镜头畸变模型和畸变参数的检测分析，让学生详尽地掌握整个分析过程。系统还设置了误差讨论板块，让学生能够直观地了解相关畸变参量对分析结果的影响，很好地解决传统光学实验中难以对各个参数进行定量分析研究的困难。

由于实验中修改参数和仪器操作存在着难度，且光学实验作为物理实验教学的重要内容，对光学实验进行计算机仿真具有重要意义。基于Matlab软件，用户可运用图形用户界面（Graphical User Interface，GUI）开发操作实现对各种控件的调用，设计和开发具有界面友好、实验现象直观、参数灵活可变换等优点的仿真实验系统，被广泛引入实践教学。王文成等［12］针对数字图像处理课程的实验教学，提出集成了6个主要模块的数字图像处理实验仿真平台。李媛等［13］针对干涉和衍射在实验中难以改变实验参数的问题，设计了杨氏双缝干涉和夫琅和费双缝衍射多光学实验仿真平台。袁志伟等［14］设计一种带有劳埃镜干涉和牛顿环2个实验的模拟仿真软件，完善了已有光学实验仿真的不足。本文采用Matlab软件所设计的基于光学条纹分析技术的镜头畸变校正实验检测与分析系统将理论分析、数值仿真和实验测量三者相结合，不仅提高了光信息专业教学中对光学条纹分析技术及相关应用的教学效果，而且该方案将科研成果融入实验教学，有利于提高学生的创新与实践能力。

1 基于条纹分析的镜头畸变校正

1.1 畸变模型

具有宽视场成像特性的广角镜头由于自身制作工艺等缺陷，会使拍摄的图片存在着一定程度上的非线性畸变，其中最为显著的径向畸变是一种以畸变中心为中心，沿着径向产生位置的偏差。常用的径向畸变模型为多项式模型［15］和除法模型［16］。本实验系统给出了单参数除法畸变模型和双参数偶数阶多项式畸变模型两种模型的分析。对于多项式模型，考虑到龙格现象实验方案采用了双参数偶数阶多项式畸变模型

式中：ru为对应无畸变点（xu，yu）到畸变中心点（x0，y0）的距离；rd为畸变点（xd，yd）到畸变中心点（x0，y0）的距离；λ1、λ2是畸变参量。畸变点（xd，yd）与相应的无畸变点（xu，yu）的关系

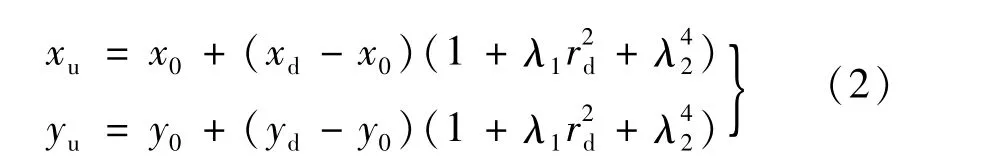
相比于多项式模型，单参数除法模型具有易于求逆的优点，其畸变模型

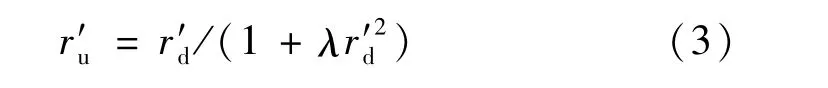
式中：r′d为畸变点（x′d，y′d）到畸变中心点（x0，y0）的距离；λ为畸变参量；r′u为对应无畸变点（x′u，y′u）到畸变中心点（x0，y0）的距离。畸变点（x′d，y′d）与相应的无畸变点（x′u，y′u）的关系

1.2 基于条纹分析的畸变测量原理

畸变原理示意如图1所示。

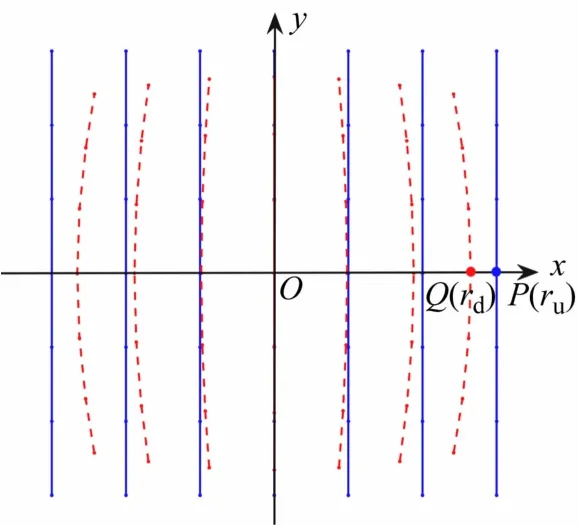
图1 畸变示意图

实线为无畸变条纹图像，虚线为发生了径向桶形畸变后的条纹图像。图中P点和Q点分别为畸变前后场景中同一物点所对应的图像点位置，畸变位置点Q所对应的畸变量Δr即为PQ的长度，畸变前后同一物点到畸变中心点位置的距离与畸变量的关系

采用纵向标准余弦型载频条纹作为测量模板，其强度分布可表示为：

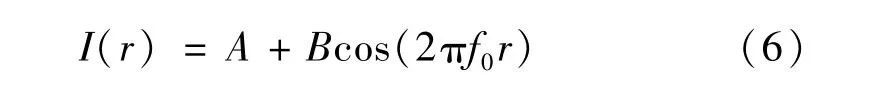
式中：A为背景光强度；B为载频条纹的振幅；φ（x，y）=2πf0r为相位；f0为基频；B/A为对比度，r为物点到光栅中心的距离。畸变条纹图像点Q记录的灰度值I（Q）对应的是无畸变条纹图像点P的灰度值

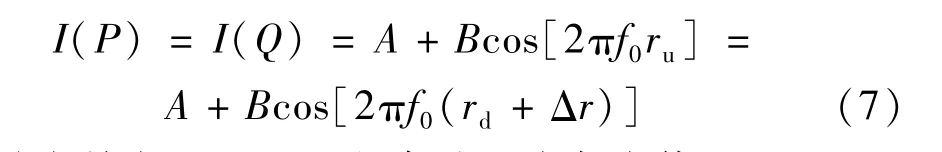
对比畸变前点Q所记录的条纹强度灰度值

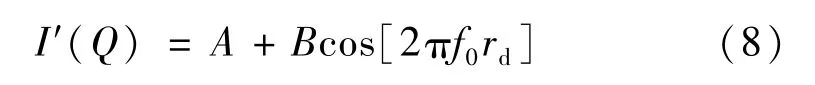
对应图像同一位置点，畸变前后条纹强度灰度值所对应的相位变化称为畸变调制相位。根据式（7），径向畸变调制相位

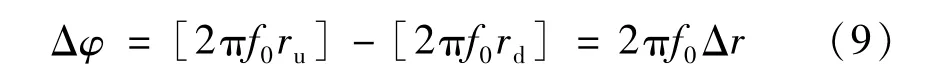
径向畸变量

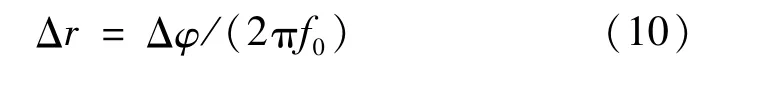
可见，通过获得载频条纹图像中径向调制相位即可得到其对应的径向畸变量Δr。根据式（1）、（5）可以获得双参数偶数阶多项式模型中径向畸变调制相位

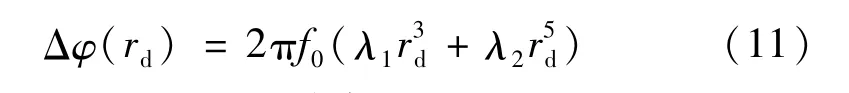
根据式（3）、（5）可以获得单参数除法模型中径向畸变调制相位

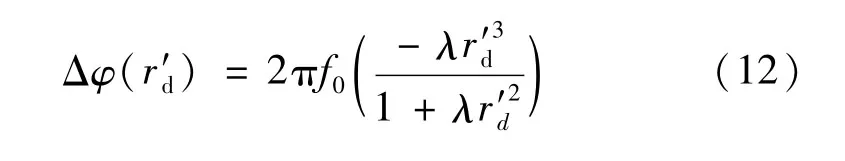
将计算分析得到的径向畸变调制相位Δφ（rd）代入式（11）、（12）进行数值拟合可获得相关畸变参量，进而实现畸变图像的校正。

1.3 畸变测量的相位解调

利用相机广角镜头拍摄采集4幅相移量分别为0，π/2，π，3π/2的载频条纹图像，其强度分布为：

结合4步相移法获得畸变条纹图的包裹相位分布：

结合解包裹算法获得连续相位值φ（x，y）。

根据瞬时频率的定义：

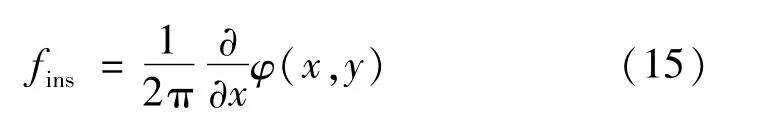
对于纵向载频条纹沿x方向对解包裹相位值求偏导，得到各个位置点的瞬时空间频率分布fins。对于径向桶形畸变，远离畸变中心畸变程度逐渐加强，条纹瞬时空间频率以畸变中心点为中心，向外延展呈现上升趋势。通过检测瞬时空间频率的最小值及其位置可获得无畸变条纹图像的基频f0及畸变中心点的位置（x0，y0）和对应中心点位置相位值φ0参数，由此计算无畸变条纹图像的相位分布：

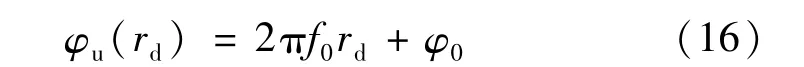
最终得到径向畸变调制相位为：

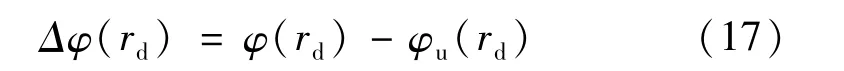
根据式（11）、（12）可计算得到畸变参量，结合后向映射进行双线性插值法对畸变图像进行校正。

2 实验系统的设计

针对光学条纹技术在镜头畸变检测及校正的应用拓展教学内容，本文基于Matlab设计开发了相应实验检测与分析系统，将理论分析、数值仿真和实验测量三者相结合，帮助学生更好地综合掌握条纹分析技术与镜头畸变校正的相关知识与应用合。学生可依托该系统，根据自身兴趣和需求进行数值仿真和实验处理。该实验平台主要模块如图2所示。

图2 实验平台主要模块

2.1 数值仿真实验系统

数值仿真系统主界面有8个主功能按钮，依据镜头畸变检测和校正过程分别实现以下功能：模拟无畸变条纹、模拟畸变条纹、畸变相位分析、畸变调制位相计算、畸变参数计算、调制位相误差分析、校正畸变图形以及误差分析及讨论，软件界面如图3所示。

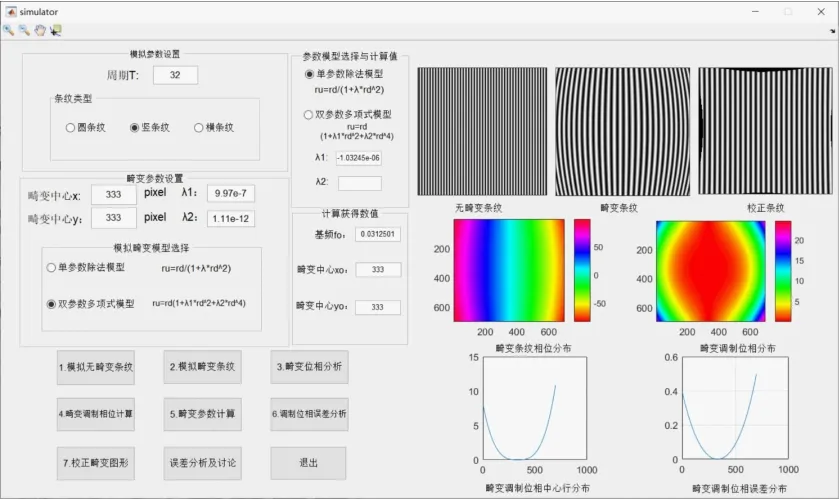
图3 数值仿真实验系统

数值仿真实验过程按照如下步骤在应用系统软件中进行操作：

步骤1模拟无畸变条纹。选择无畸变模型，输入测量模板的仿真参数，包括载频条纹的周期。模型系统提供竖载频条纹、横载频条纹和圆载频条纹，系统默认采用载频条纹图像大小为700×700像素。

步骤2模拟畸变条纹。选择畸变模型，并输入畸变参量以及畸变中心的位置。通过给定不同的畸变参量可直观获得不同畸变程度的图像。系统设置条纹周期T的范围在（3，129）像素，畸变中心点的范围在（350±100，350±100）像素，当设置超过这些范围时，系统会弹出窗口让操作者重新输入。考虑到当透镜中心与相机电荷耦合器件（Charge-coupled Device，CCD）中心的偏移或者传感器平面相对于透镜轻微倾斜的情况下，畸变中心会偏离图像中心，实验系统中可以对畸变中心点的位置进行设置。

步骤3畸变位相分析。对畸变条纹图像使用四步相移法与解包算法计算对应的相位分布，绘制相应图形。

步骤4畸变调制位相计算。数值计算无畸变条纹相位分布，获得畸变调制相位，并绘制畸变调制位相分布图与畸变调制位相中心行分布图。

步骤5模型参数计算。根据选定的畸变模型，通过数值拟合计算畸变参量。

步骤6调制位相误差分析。根据原始模拟的理想畸变相位分布计算调制相位误差分布，并绘制相应畸变中心行的调制相位误差分布图。

步骤7校正畸变图形。根据畸变参量，采用后向映射结合双线性插值实现条纹图像的畸变校正。

步骤8数值仿真程序中设计了对畸变条纹图像的基频和畸变中心位置参量的量化讨论模块，如图4所示。在计算畸变量时，可通过系统误差设置面板，自主设置数值计算基频f0及畸变中心点（x0，y0）的取值，展开相关畸变参量对分析结果的量化对比讨论。数值仿真讨论的结果以不同参数的校正结果图进行展示。

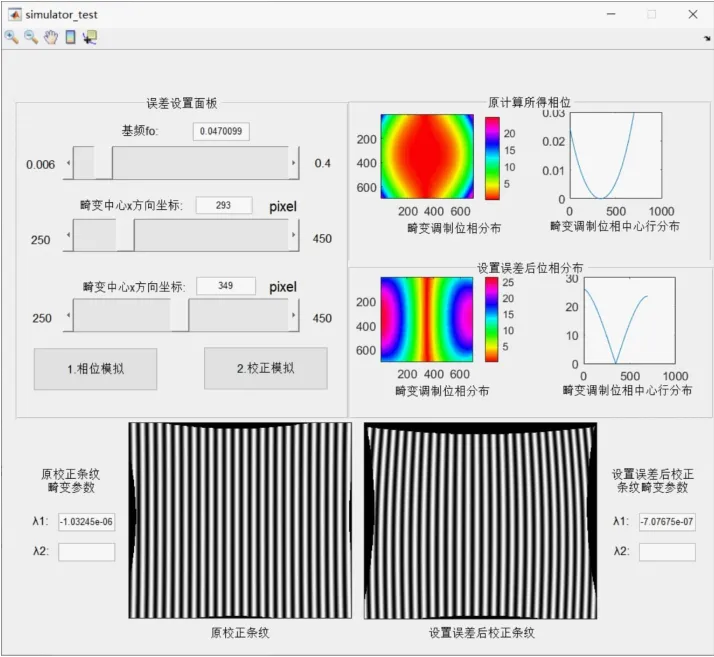
图4 误差分析讨论模块

应用界面左上角提供了图像放大、缩小、平移及数据游标工具，学生可对图像进行详细的分析，观察矫正过程中各个过程的特征与变化，加深对光学条纹分析技术在畸变校正中作用的理解。

2.2 光学实验及处理系统设计

实验系统装置示意如图5所示。

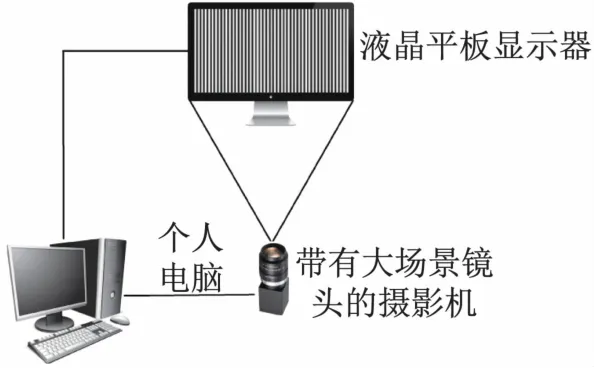
图5 实验系统装置示意图

采用液晶平板显示器（Liquid Crystal Display，LCD）4幅相移量分别为0，π/2，π，3π/2的载频条纹图像作为测量模板，使用带有广角镜的CCD拍摄载频条纹图像，广角镜的光轴垂直于液晶平板显示器LCD。将拍摄所得的畸变载频条纹图像输入镜头畸变校正实验检测与分析系统中进行畸变量检测，以实现畸变图像校正。

镜头畸变校正实验检测与分析系统的实验主界面如图6所示。

图6 实验检测分析系统

该系统包括畸变载频条纹的读入、畸变位相分析、畸变参数计算以及实景图校正4个模块功能。该系统主要提供对纵向载频条纹，横向载频条纹和圆条纹的分析以及双参数偶数多项式模型和单参数除法模型两种畸变模型的参数检测。具体实现过程如下：

（1）输入模板图像。读入实验拍摄的4幅畸变载频条纹图像。

（2）位相分析。数值计算无畸变条纹相位分布，获得畸变调制相位，并描绘畸变调制位相分布图与畸变调制位相中心行分布图。

（3）畸变调制位相计算。数值计算无畸变条纹相位分布，获得畸变调制相位，并描绘畸变调制位相分布图与畸变调制位相中心行分布图。

（4）畸变参数计算。根据选定的畸变模型，通过数值拟合计算畸变参量。

（5）实景图校正。读入拍摄得到的畸变实景图像，根据畸变参量，采用后向映射结合双线性插值实现对实验所拍摄的畸变实景图进行校正，并通过按键对校正图像进行保存。如图7（a）、（b）所示，分别为实验拍摄的畸变棋盘格图像以及对应的校正图像。

图7 棋盘格校正实验

3 结语

本文采用Matlab软件，设计了一套基于光学条纹分析技术的镜头畸变校正实验检测与分析系统，该系统将理论分析、数值仿真和实验测量三者结合，实现了实验参数的灵活设置和误差分析的量化对比讨论，开拓了光学条纹分析技术在镜头畸变检测校正中的应用教学。该系统用户界面具有友好、交互性强、易于扩展等特点，借助该系统开展实验教学活动，有助于学生理解和掌握光学条纹技术的技术原理和分析方法，帮助学生更好地掌握条纹分析技术与镜头畸变校正的应用，提高学生在光信息专业领域的综合能力。