增程器轴系不对中故障动力学响应特性分析

许小伟,刘振兴,严运兵,南 欣,邢家铭

(武汉科技大学汽车与交通工程学院，湖北 武汉,430065)

增程式电动汽车作为混合动力汽车向纯电动汽车的平稳过渡车型，以其效率高、电池容量小、不会因缺电抛锚等优点受到广泛关注，是当下解决能源危机、环境污染等问题的重要途径之一[1-2]。增程器是增程式电动汽车的辅助动力来源，依靠联轴器来连接发动机和发电机部件传递动力，具有运动部件多、激励来源广、易损率高等特点。60%的旋转机械故障是由不对中故障引起的，而增程器轴系受到两端传递的扭矩和激励作用导致不对中故障更容易发生。增程器轴系不对中故障不仅会使增程式电动汽车产生噪声和振动，且不对中故障所产生的轴向激励和径向激励还可能导致二次故障的发生[3]，因此进行增程器轴系不对中故障的诊断和研究显得尤为重要。

近年来，国内外研究人员对不对中故障动力学分析进行了大量研究。黄志伟等[4]通过推导建立机组转子不对中-碰摩耦合故障的动力学模型和微分方程，以不对中平行量和偏角量为控制参数研究了系统异常振动的故障机制。李自刚等[5]基于两转子间运动的几何关系和位移约束条件推导了在非线性油膜力作用下平行不对中转子系统的动力学模型，探讨了平行不对中故障时系统的非线性振动特征。Qi等[6]和Haroun等[7]通过搭建实验台架进行不对中故障的设置，分析联轴器三种不对中故障，提出了一种基于瞬时频率估计的阶比跟踪分析方案，采集振动信号进行故障分类。雷文平等[8]通过研究齿式联轴器的运动规律和受力情况，推导出齿式联轴器不对中故障产生的径向力表达式，得出不对中量和响应之间的量化关系。温斌等[9]使用Adams软件对发电机故障系统进行仿真，通过对机组振动测试与频谱分析，对运行过程中常见的不对中、不平衡及安装误差等引起振动问题分别进行评估。上述研究从不同角度讨论了不对中故障产生的动力学特性，但常常忽略了不同类型的不对中故障所产生的差异，如何辨识不同类型的不对中故障并提取故障诊断特征参数具有非常高的应用价值。一般研究中大多搭建简化的转子实验台架，简化后的系统忽略了自身结构特性，导致与实际相差较大，而通过实物进行试验会给机械系统带来不可逆的损坏。为此，本文通过分析增程器轴系在不对中故障时的运动状态与受力情况，建立增程器轴系的动力学模型，并利用多体动力学软件对增程器轴系平行不对中、偏角不对中、综合不对中三种类型的故障进行仿真，分析不同类型不对中故障产生的动力学响应特性，以期为增程器轴系的维护和不对中故障诊断提供参考。

1 增程器轴系动力学模型

增程器轴系不对中故障示意图如图1所示。图1中，δ为联轴器平行不对中量，ΔL为左右联轴器之间安装距离，γ为联轴器偏角不对中量。由于增程器轴系除了发生平行不对中和偏角不对中外，还可能发生综合不对中故障，此种形式下转子受力是平行不对中和偏角不对中故障的组合。在建立模型时，平行不对中故障和偏角不对中故障均对联轴器系统产生不对中激励，为同时兼顾这三种不对中故障形式，用当量不对中量ΔE表示：

ΔE=δ+ΔLtanγ

(1)

式中：仅存在δ表示增程器轴系只发生了平行不对中故障，仅存在γ表示增程器轴系只发生了偏角不对中故障，δ、γ同时存在时表示增程器轴系发生了综合不对中故障，δ、γ全部为零则表示联轴器轴系没有发生不对中故障。

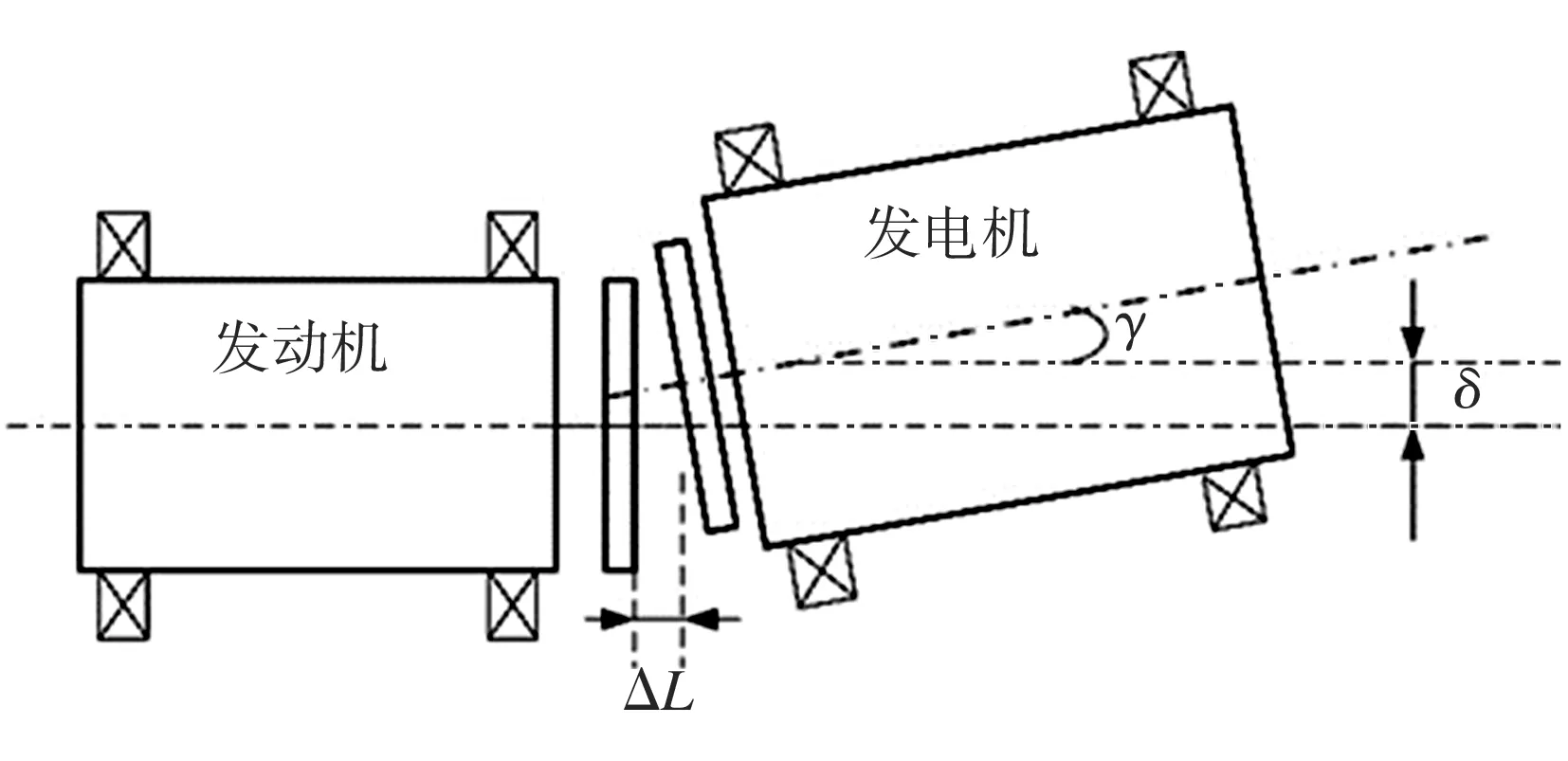
图1 增程器轴系不对中故障示意图

Fig.1Schematicdiagramofshaftingmisalignmentfaultforrangeextender

由于联轴器动态中心角速度为转子旋转速度的二倍[10]，设转子旋转速度为ω，θ为初试相位角，则联轴器中间质心运动轨迹可表示为：

(2)

设联轴器在质心处的等效质量为m,增程器轴系存在不对中故障时，对于增程器系统的广义力可分为内部激励和外部激励，忽略增程器部件所受到的额外激励，增程器轴系不对中故障引起的内部激励作用按照x、y轴方向分解为Fxc、Fy c，其表达式为：

(3)

偏角不对中故障造成发动机与发电机轴之间出现一个倾斜角度γ，将发电机轴的受力投影到y-z平面，如图2所示。图2中，β为投影轴与y轴的夹角，发动机输出转矩T经联轴器分解成两部分作用在发电机轴上，分别为Tz和Ts，其中Ts可以进一步沿x轴和y轴分解为两个弯矩分别为TX、TY[11]，其表达式为：

(4)

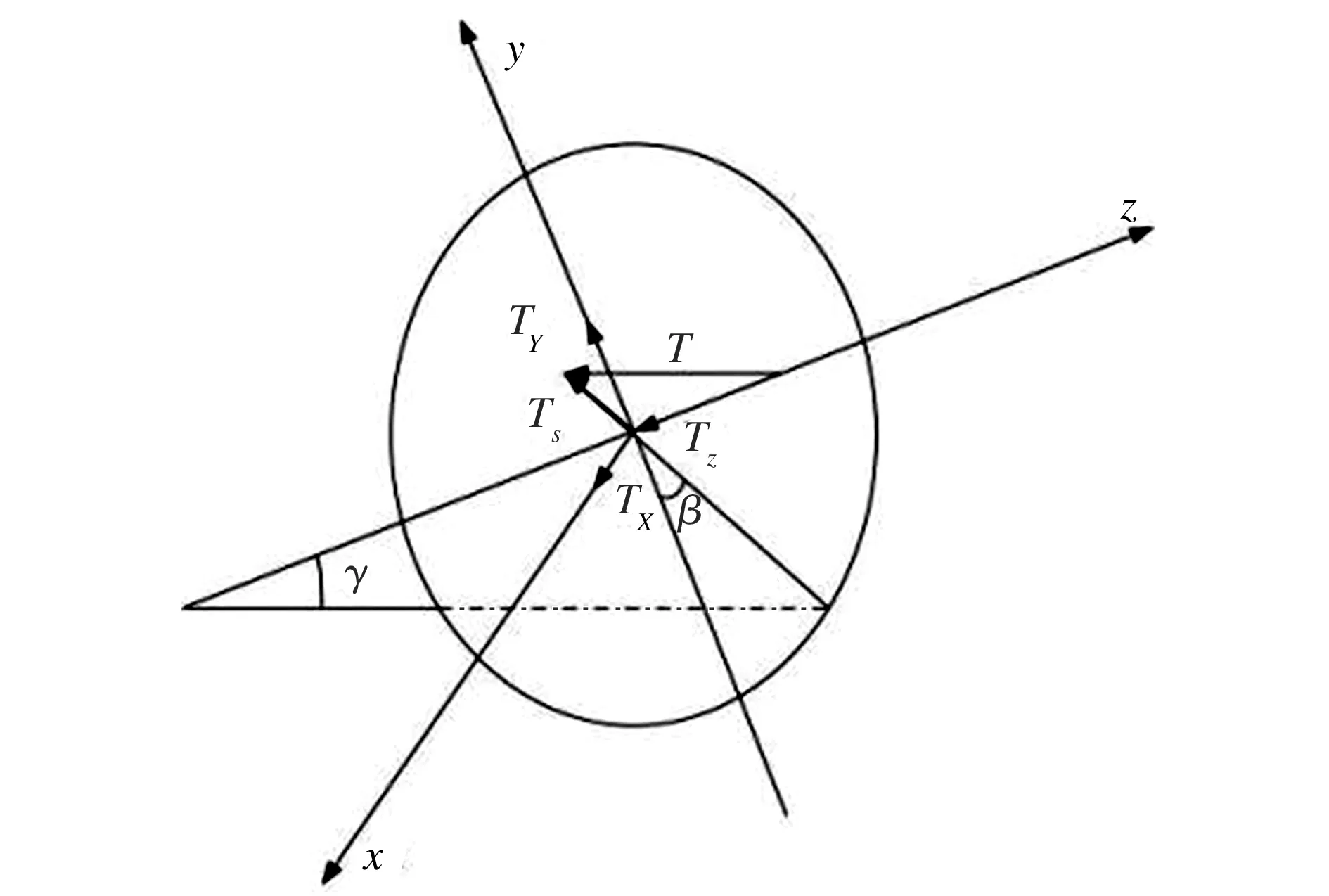
图2 偏角不对中时发电机轴受力投影分解图

Fig.2Projectiondecompositiondiagramofforceongeneratorshaftunderangulardeviationmisalignment

综合考虑不对中故障给增程器轴系带来的激励作用，得到不对中故障时转子系统的力学模型，写成矩阵形式为：

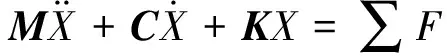
(5)

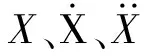
联轴器运动示意图如图3所示。假设两个半联轴器的圆心坐标分别为O1(x1,y1)、O2(x2,y2)，其偏心距为e，初始相位角为0，则有：

(6)

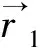
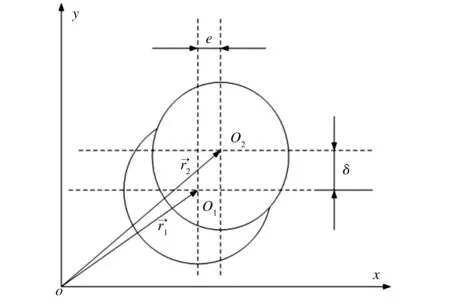
图3 联轴器运动示意图Fig.3 Schematic diagram of coupling motion

向的单位向量。联轴器两侧在运动过程中始终保持恒定的不对中量δ，即根据运动方程的约束条件可得：

(x1-x2)2+(y1-y2)2=δ2

(7)

由图3可知，将O2投影至O1平面，联轴器存在平行不对中量δ，则联轴器半侧由圆形变为偏心距为e的椭圆，将点O2(x2,y2)以点O1(x1,y1)坐标来表示，则有：

(8)

式中：φ为联轴器两侧在动态坐标系中的相位角,φ=ωt+θ。

建立了系统的动态坐标后，提取联轴器两侧运动特征进行分析，联轴器两侧的速度参数可表述为：

(9)

对于含有刚性联轴器的系统，可将发动机、发电机质量分别等效至联轴器两侧在质心处的质量，忽略轴端的弹性势能，不考虑支撑处发生额外位移，则联轴器系统中的动能(Q)、势能(U)及耗散能(ψ)分别为：

(10)

式中：m1、m2分别为发动机、发电机质量；J1、J2分别表示联轴器两侧的转动惯量；k1、k2为联轴器两侧的等效刚度；c1、c2为联轴器两侧的黏性阻尼系数。假定联轴器左右对称，且不考虑内部阻尼，即m1=m2,k1=k2,c1=c2。

利用第二类拉格朗日方程,对公式 (10)进行求解，并联立公式(3)、公式(8)，即可得到增程器轴系的动力学微分方程组：

(11)

2 动力学响应特性

为分析增程器轴系发生不对中故障时的振动响应特性，需对微分方程组求解提取正常状态与故障状态下的响应信号。计算求解所用的参数分别为：m1=m2=25 kg，ΔL=2 mm，e=2 mm，k1=k2=2.5×106N/m。在发动机输出转速为1500 r/min时提取不同不对中状态下发电机主轴轴心的X、Y向时域波形及频谱响应。

增程器轴系不对中故障时X、Y向位移的时域图如图4所示。从图4中可以看出，当轴系未发生故障时，其X、Y向振动波形表现为正弦波形(见图4(a))；当发生平行不对中故障时，其X、Y向的振动波形发生了明显变化，系统开始趋于不稳定状态，有双波形状的出现(见图4(b))；而在偏角不对中状态下的时域响应则更加不稳定，且双波形状更加明显(见图4(c))，由此表明，不同类型不对中故障的系统振动所呈现的时域波形不同。

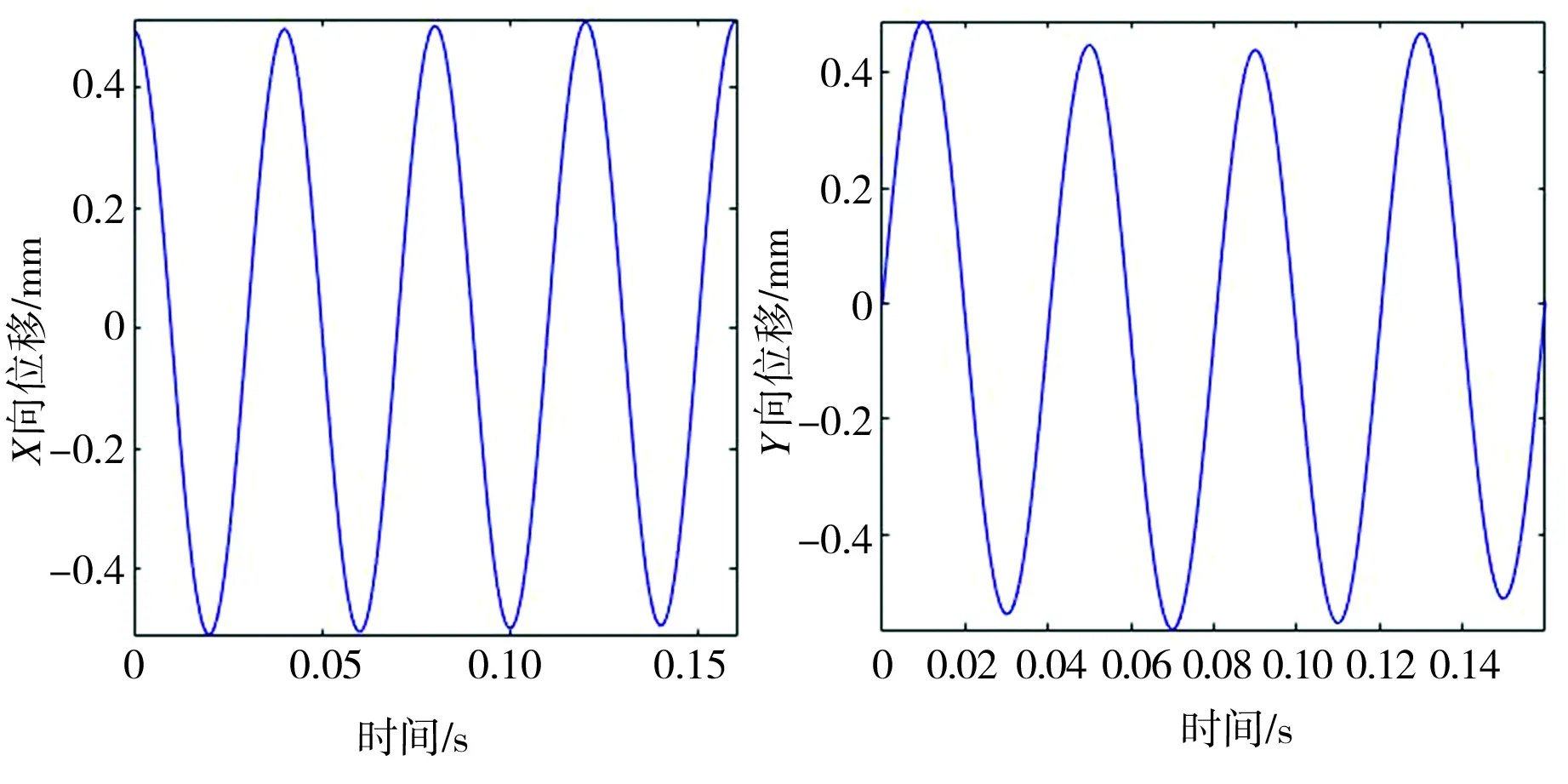
(a)正常状态

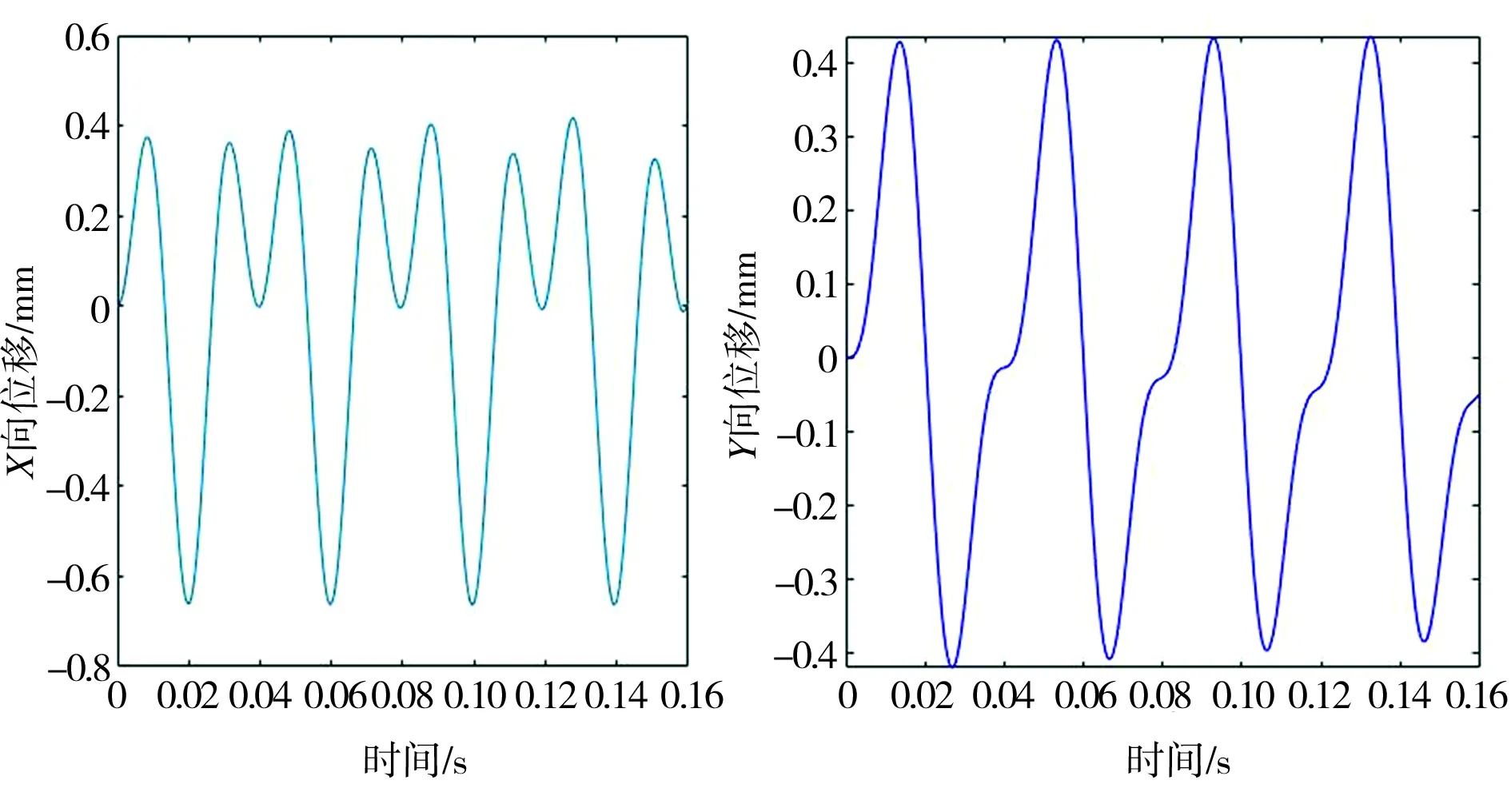
(b)δ=0.5

(c)γ=1°

Fig.4TimedomaindiagramsofXandYdirectionaldisplacementunderextendershaftmisalignment

不同类型不对中故障时系统振动响应频谱图如图5所示。 从图5 (a)、图5 (b) 中可以看出，平行不对中故障下振动频谱响应以1谐次、2谐次为主，2谐次频谱幅值大于1谐次的频谱幅值，与正常状态下(见图5(e))相比，平行不对中故障使1谐次的频谱幅值稍微变大，2谐次频谱幅值变化明显，且随不对中量的增加，1谐次频谱幅值变化不明显，2谐次的频谱幅值明显增大。从图5(c)、图5 (d) 中可以看出，偏角不对中故障的发生致使1谐次和2谐次的频谱幅值均有所增长，且1谐次的频谱幅值明显增大，而随着不对中量的增大，1谐次的频谱幅值稍微变大、2谐次的频谱幅值有所减小。从图5(f)、图5 (g)、图5 (h)三种综合不对中故障下系统的振动频谱变化可以看出，当平行不对中量固定时，随着偏角量的增大，1谐次的频谱幅值大幅增长，2谐次的频谱幅值减小；当偏角不对中量一定时，随着平行不对中量的增大，1谐次的频谱幅值稍微减小，2谐次的频谱幅值急剧增大。

(a)δ=0.5 mm (b)δ=1.0 mm (c)γ=1° (d)γ=2°

(e)正常状态 (f)δ=0.5 mm，γ=1° (g)δ=0.5 mm，γ=2° (h)δ=1.0 mm，γ=2°

图5不同类型不对中故障时系统振动响应频谱图

Fig.5Frequencyspectrumofvibrationresponseofsystemswithdifferentshaftmisalignmentfaults

3 仿真实验验证

根据增程器实际尺寸大小建立某型号增程器轴系的三维模型，导入有限元程序中生成中性替换文件，最后在多体动力学软件中添加连接副、加载约束、设置驱动，建立增程器刚柔混合多体动力学模型如图6所示。通过改变联轴器的相对位置，并添加附加力矩，可模拟不同类型的不对中故障。为与上述理论分析对应，设置发动机输出转速稳定在1500 r/min下进行仿真，并提取各参数进行分析。

图6 增程器刚柔混合多体动力学模型

Fig.6Rigidflexiblehybridmulti-bodydynamicsmodelforrangeextender

模拟不同不对中故障类型的系统振动响应频谱图如图7所示。从图7中可以看出，正常状态下以1谐次频谱为主(见图7(e))，这与动力学建模得到的结论相一致；随着平行不对中量的增大,除了1谐次的频谱外，又出现了2、3等谐次的频谱，2谐次的频谱幅值随着不对中量的增大而增大，当平行不对中量为1.0 mm时， 2谐次的频谱幅值急剧增大， 1谐次和3谐次的频谱幅值整体变化不大(见图7(a)、图7(b))。从图7(c)、图(d)中可以看出，偏角不对中故障时系统的振动响应频谱成分主要分布在整数谐次处，随着故障程度的加深，1谐次、2谐次的频谱幅值随之增大，且1谐次成分变化更为明显。从图7(f)～图7 (h) 中可以看出，综合不对中故障时系统的振动响应频谱成分主要分布在1谐次、2谐次，当平行不对中量一定时(见图7(f)和见图7(g))，偏角不对中量的增大使1谐次的频谱幅值增大、2谐次的频谱幅值减小；当偏角不对中量一定时(见图7(g)和图7(h))，平行不对中量增加会带来1谐次的频谱幅值稍微增大、2谐次的频谱幅值明显增大，这与动力学响应特性的分析结果基本相吻合。

通过以上分析能够判定出不对中故障类型的动力学响应特性差异。然而仿真是建立在已知的不对中量和设定的转速条件下进行的，在实际不对中故障诊断过程中，故障状态往往是未知的，不对中量的数值也无法获取，所提取的少量数据不能够很好地进行不对中故障辨识。因此要对三种不对中故障状态进行精确的辨识，还需要对不对中故障的动力学响应特性进行更深入的研究。

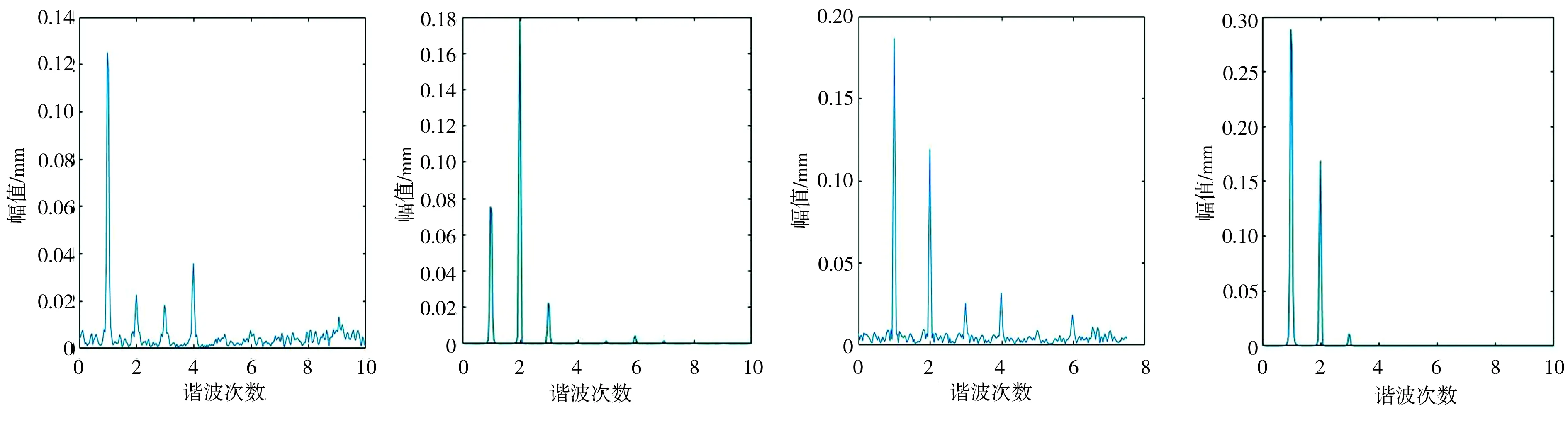
(a)δ=0.5 mm (b)δ=1.0 mm (c)γ=1° (d)γ=2°

(e)正常状态 (f)δ=0.5 mm,γ=1° (g)δ=0.5 mm,γ=2° (h)δ=1.0 mm,γ=2°

图7模拟不同不对中故障类型的系统振动响应频谱图

Fig.7Frequencyresponsespectrumofsystemsimulatedwithdifferentshaftmisalignmentfaults

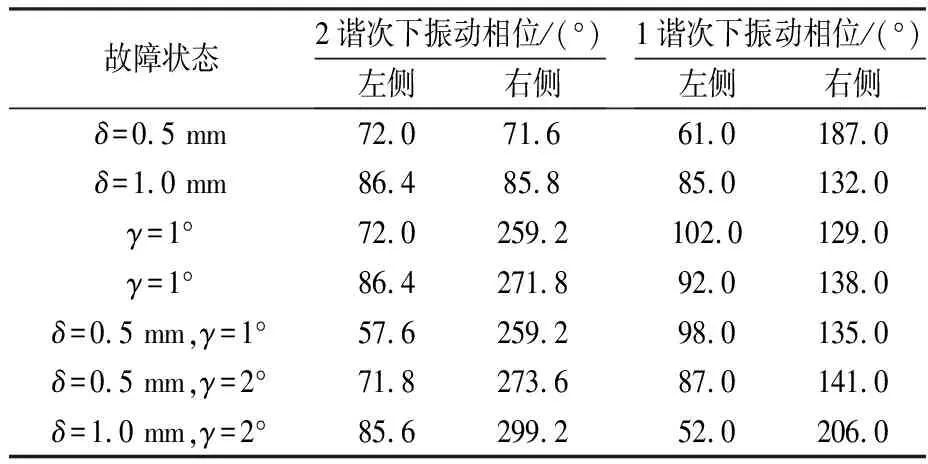
为了进一步研究不对中故障下联轴器轴系两侧的相位特性，对三种不对中情况下轴系振动谐次信号进行快速傅里叶逆变换，提取联轴器轴系左右两侧的振动相位信息。表1为三种不对中故障时联轴器轴系左右两侧在1谐次和2谐次下的振动相位。从表1中可以看出，在1谐次下，不对中故障类型与轴系两侧相位信息无直接相关性，无法进行不对中故障类型的辨识；在2谐次下，发生平行不对中故障时，轴系两侧相位基本相同，在两种偏角不对中状态下，轴系两侧相位差分别为187.2°、185.4°。由于仿真模型并不是完全的理想状态，因而在平行不对中故障和偏角不对中故障中相位差不是严格的0°和180°，因此可以认为，平行不对中故障下联轴器左右两侧在2谐次下的振动相位差接近0°，偏角不对中故障状态下联轴器左右两侧在2谐次下的振动相位差接近180°。从表1中还可以看出，综合不对中故障下轴系两侧在2谐次下的振动相位差依次为201.6°、201.8°、213.6°，即综合不对中故障下轴系左右两侧在2谐次下的振动相位差均大于180°。由此表明，轴系左右两侧在2谐次下的振动相位差特性可以作为区分平行不对中故障、偏角不对中故障及综合不对中故障辨识的重要特征。

表1三种不对中故障时联轴器轴系左右两侧振动相位

Table1Vibrationphaseonbothsidesofcouplingshaftingunderthreetypesofmisalignmentfaults

故障状态2谐次下振动相位/(°)左侧右侧 1谐次下振动相位/(°)左侧右侧δ=0.5 mm72.071.661.0187.0δ=1.0 mm86.485.885.0132.0γ=1°72.0259.2102.0129.0γ=1°86.4271.892.0138.0δ=0.5 mm,γ=1°57.6259.298.0135.0δ=0.5 mm,γ=2°71.8273.687.0141.0δ=1.0 mm,γ=2°85.6299.252.0206.0

4 结论

(1)系统振动频谱中1谐次和2谐次的幅值可作为增程器轴系不对中故障诊断特征参数，平行不对中导致2谐次频谱幅值的大幅增长，偏角不对中使1谐次频谱幅值变化明显。

(2)增程系轴系左右两侧在2谐次下的振动相位差可作为不对中故障类型的辨识依据，其中平行不对中故障下轴系两侧振动相位差接近0°；偏角不对中故障下轴系两侧振动相位差接近180°；综合不对中故障下轴系两侧振动相位差远大于180°。