几何特性对薄壁箱梁畸变效应的影响
2020-01-16王晨光张元海
王晨光 张元海
(兰州交通大学土木工程学院, 兰州 730070)
箱形梁在偏心荷载作用下发生弯扭耦合变形.受薄壁的影响,其畸变变形显著,是设计过程中必须考虑的问题之一.近年来,国内外许多学者针对箱形梁畸变效应开展了研究工作,建立了不同的分析理论[1-10].Chidolue等[11]基于符拉索夫广义坐标法的基本原理,求解得到三室全斜腹板箱梁的畸变控制微分方程,并利用三角级数法计算箱形梁的畸变变形.张元海等[12]以箱形梁产生畸变变形时的畸变角为基本未知量,应用基于最小势能原理的能量变分法,分析箱形梁布置双层悬臂版时的畸变效应.Wright等[13]利用弹性地基梁的挠度来比拟箱形梁的畸变角,提出了计算箱形梁畸变效应的弹性地基梁比拟法.李立峰等[14]采用基于共轭梁理论的纽玛克法,建立了计算变截面波形钢腹板组合箱梁畸变正应力的解析理论,并采用空间有限元方法进行了验证.
上述用于分析箱形梁畸变效应的不同解析理论虽然取得了较高精度,但求解过程复杂,不便于理解.本文通过理论推导,引入了能直观反映箱形梁畸变效应的横截面畸变几何特性,以便为设计人员提供参考.
1 畸变总势能
箱形梁截面尺寸如图1所示.图中O为截面形心,x轴和y轴分别为过截面形心O的水平轴与竖直轴.箱形梁腹板、底板、悬臂板的长度分别为a1、a2、d,腹板、底板、顶板的厚度分别为t1、t2、t3.

图1 箱形梁截面尺寸示意图
沿梁跨度方向取dz=1的一段单位长度箱梁框架进行分析,框架发生畸变时的变形图如图2所示.假设角点B处的畸变角为γ2(z).为简化计算,取一半结构进行分析,如图3所示.
当顶板上的水平力F=1时,G点的水平位移为
(1)

图2 横向框架变形图
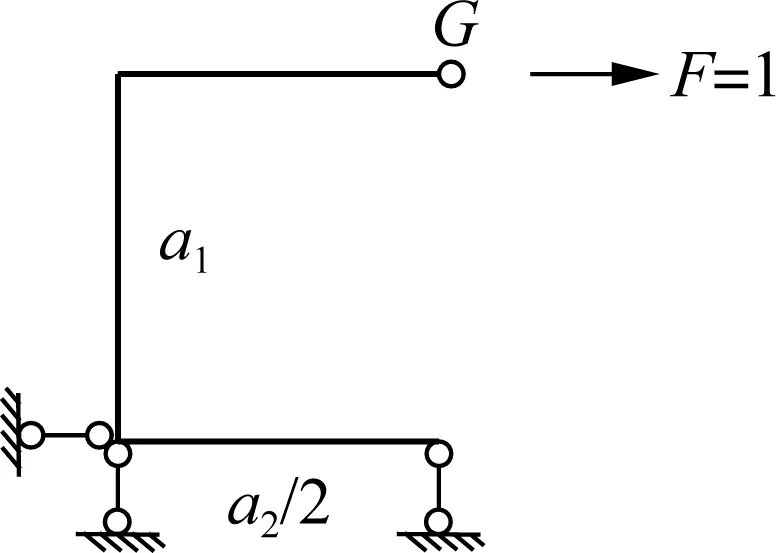
图3 基本结构示意图
式中
式中,I1、I2、I3分别为单位长度上腹板、底板和顶板惯性矩;E为弹性模量;X为基本结构上G点处的竖向力.
事实上,顶板水平位移等于γ2a1,作用在顶板上的力P1(z)=γ2a1/δG.故可以得到角点A、B、C、D处的弯矩MA,MB,MC,MD分别为
(2)
(3)

横向框架畸变应变能为
(4)
令
则上式可简写为
(5)
式中,M为单位长度箱梁框架上的横向弯矩.
箱形梁发生畸变翘曲时的畸变翘曲应力分布见图4.设σ1、σ2分别为角点A、B处的畸变翘曲正应力;Md1、Md2、Md3分别为腹板、底板及顶板上的畸变翘曲正应力在自身平面合成的内力矩;v1、v2、v3分别为腹板、底板及顶板在自身平面内的挠度;Id1、Id2、Id3分别为腹板、底板及顶板在自身平面内弯曲时的惯性矩;h为箱形梁的梁高.根据初等梁的弯曲理论可得

图4 畸变翘曲正应力分布
(6)

根据变形几何关系,可以得到畸变角γ2的表达式为
(7)
对式(7)求导,并将式(6)代入,经过整理可得
(8)

故畸变翘曲应变能U2为
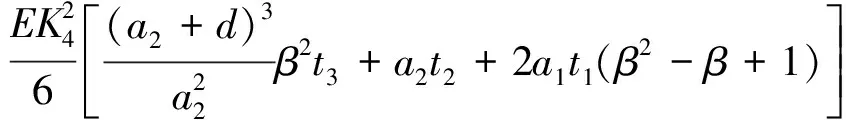
(9)
令
则式(9)可简写为
(10)
当外荷载P(z)作用在箱形梁顶板与腹板交点处时,荷载势能U3可以表达为
(11)
不考虑剪切变形的影响时,箱形梁在畸变荷载作用下的总势能U由周边横向弯曲应变能U1、板平面内翘曲应变能U2以及荷载势能U3三部分组成,即
U=U1+U2+U3=
(12)
2 畸变控制微分方程
根据最小势能原理,对畸变总势能进行变分可以得到关于畸变角γ2的畸变控制微分方程为
(13)

(14)
λ为箱形梁的畸变几何特性参数,直观反映了箱形梁抵抗畸变变形的能力.通过对几何特性参数λ的计算与分析,可以在不求解复杂方程式(13)的情况下研究箱形梁的畸变效应.λ的量纲为m-1.
与箱形梁畸变效应有关的广义力畸变双力矩Bwd与畸变矩Mwd分别为
(15)
Mwd=-EIwdγ‴2
(16)

常见工程结构的边界约束条件为:
① 刚性固定的支座约束.箱形梁在刚性固定支座处不能发生畸变变形,因此畸变角与畸变位移均为零,即
γ=0,γ′=0
(17)
② 简支梁的端部设置有刚性横隔板.横隔板的约束使得箱形梁在梁段不能发生畸变变形,即畸变角为零,且在端部横截面上的畸变翘曲正应力为零,即
γ=0,γ″=0
(18)
③ 自由悬臂端且没有设置横隔板.箱形梁在自由悬臂端的畸变翘曲正应力与畸变翘曲剪应力均为零,即
γ″=0,γ‴=0
(19)
根据畸变控制微分方程,结合不同约束情况下的边界条件,可分别求得不同约束情况下的畸变角、畸变双力矩和畸变矩的表达式.对于两端设置刚性横隔板的简支箱梁,在跨中作用集中畸变矩MD时,通过畸变控制微分方程和边界条件,可以得到左半跨任意截面上的畸变双力矩和畸变矩的表达式分别为
[sin(λz)cosh(λz)+cos(λz)sinh(λz)]+
[sin(λz)cosh(λz)-cos(λz)sinh(λz)]
(20)
cos(λz)cosh(λz)]
(21)
式中
[sin2(λl)+sinh2(λl)]-1
对于两端设置刚性横隔板的简支箱梁,沿梁跨满跨作用分布畸变矩mD时,任意截面上的畸变角和畸变双力矩的表达式分别为
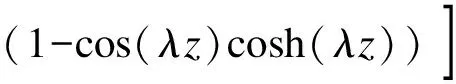
(22)
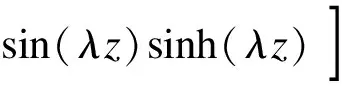
(23)
3 畸变翘曲应力
由式(8)和式(15),根据畸变翘曲正应力在横截面上线性分布的规律,可得畸变翘曲正应力σwd的计算公式为
(24)
式中,ωd为畸变翘曲率.
采用箱壁微元体的纵向平衡条件,对箱形梁横截面上的畸变翘曲剪应力进行分析,通过计算可以得到
(25)
式中,qwd=τwdt为畸变翘曲剪流,其中,τwd为畸变翘曲剪应力,t为箱壁厚度.
将式(25)对s积分可得
(26)
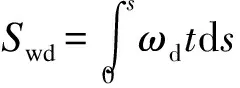
为了求得常剪流qwd0,可利用畸变翘曲剪流在箱梁横截面上不形成扭矩的条件,即∮qwdρds=0,其中,ρ为力臂.代入式(26),可求得常剪流为
(27)
将式(27)代入式(26)可得
(28)

4 数值算例及参数分析
算例1为一个跨度l=1.1 m的简支箱形梁模型,横截面尺寸见图5.箱形梁壁厚均为3 mm,材料弹性模量E=3.268 GPa.在箱形梁两端布置横隔板,跨中不设置横隔板.有限元计算过程中,设置横隔板与组成箱形梁的各板件刚性连接,且其弹性模量与各板件相同.采用如下2种荷载工况进行计算:① 集中荷载P=294 N作用在跨中横截面顶板与腹板交点处;② 满跨均布荷载p=300 N/m作用在箱形梁顶板与腹板交点处.在跨中横截面上布置计算点Ⅰ、Ⅱ、Ⅲ.采用本文方法和有限元法分别对箱形梁畸变翘曲正应力和畸变翘曲剪应力进行计算.有限元法计算时采用通用有限元软件ANSYS中的SHELL63单元,箱形梁共离散为21 560个单元.

图5 箱形梁截面简图(单位:mm)
表1给出了工况1下跨中横截面上不同计算点处畸变翘曲正应力和畸变翘曲剪应力的计算结果.由表可知,采用本文方法计算的箱形梁畸变应力与ANSYS计算结果吻合.
图6给出了工况2下箱形梁跨中横截面上畸变翘曲正应力在顶板上的分布情况.由图可知,畸变翘曲正应力在顶板上呈线性分布,在顶板中间畸变翘曲正应力为零.采用本文方法计算所得的跨中横截面上的畸变翘曲正应力分布规律与ANSYS有限元计算所得规律一致.
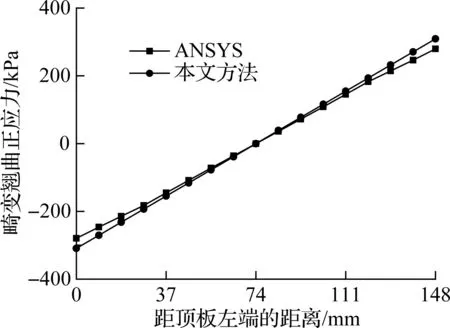
图6 顶板上畸变翘曲正应力分布图
算例2为一个跨度L=40 m的等截面简支梁桥,其横截面尺寸见图7.该箱梁采用C40混凝土,材料的弹性模量E=34 GPa.荷载为箱形梁跨中截面作用一偏心荷载P=451.0 kN,偏心距e=2.35 m.简支梁的两端设置厚度为1.2 m的横隔板,跨中不设置横隔板.计算点Ⅰ、Ⅱ分别为左腹板与顶、底板的交点.采用通用有限元软件ANSYS中的SHELL63单元对该箱梁进行有限元分析计算,该箱梁共离散为12 331个单元.

图7 箱形梁截面简图(尺寸单位:cm)
分别采用本文方法和ANSYS有限元法对箱形梁的畸变效应进行计算.表2为跨中横截面上计算点Ⅰ、Ⅱ处的畸变翘曲正应力和畸变翘曲剪应力的计算结果.由表可知,本文方法计算所得的畸变翘曲应力与ANSYS壳单元计算所得的结果吻合良好,尤其是畸变翘曲正应力,其计算结果具有较高的精度.

表2 畸变翘曲应力比较 kPa
当桥梁结构跨高比发生改变时,箱形梁跨中横截面上畸变内力的变化规律如图8所示.在分析跨高比对桥梁结构畸变效应影响过程中,保持箱形梁横截面尺寸不变,通过改变梁跨长度来实现跨高比的变化.由图可知,跨中截面的畸变矩不随桥梁结构跨高比的变化而变化,保持为一定值.而随着箱形梁跨高比的增加,跨中横截面上的畸变翘曲双力矩呈现出先减小后增大的趋势.对于与本例箱形梁箱壁厚度类似的箱梁,当跨高比L/h约为16时,桥跨结构上的畸变双力矩最小.在跨高比小于16时减小幅度较大,大于16时增长幅度较小.
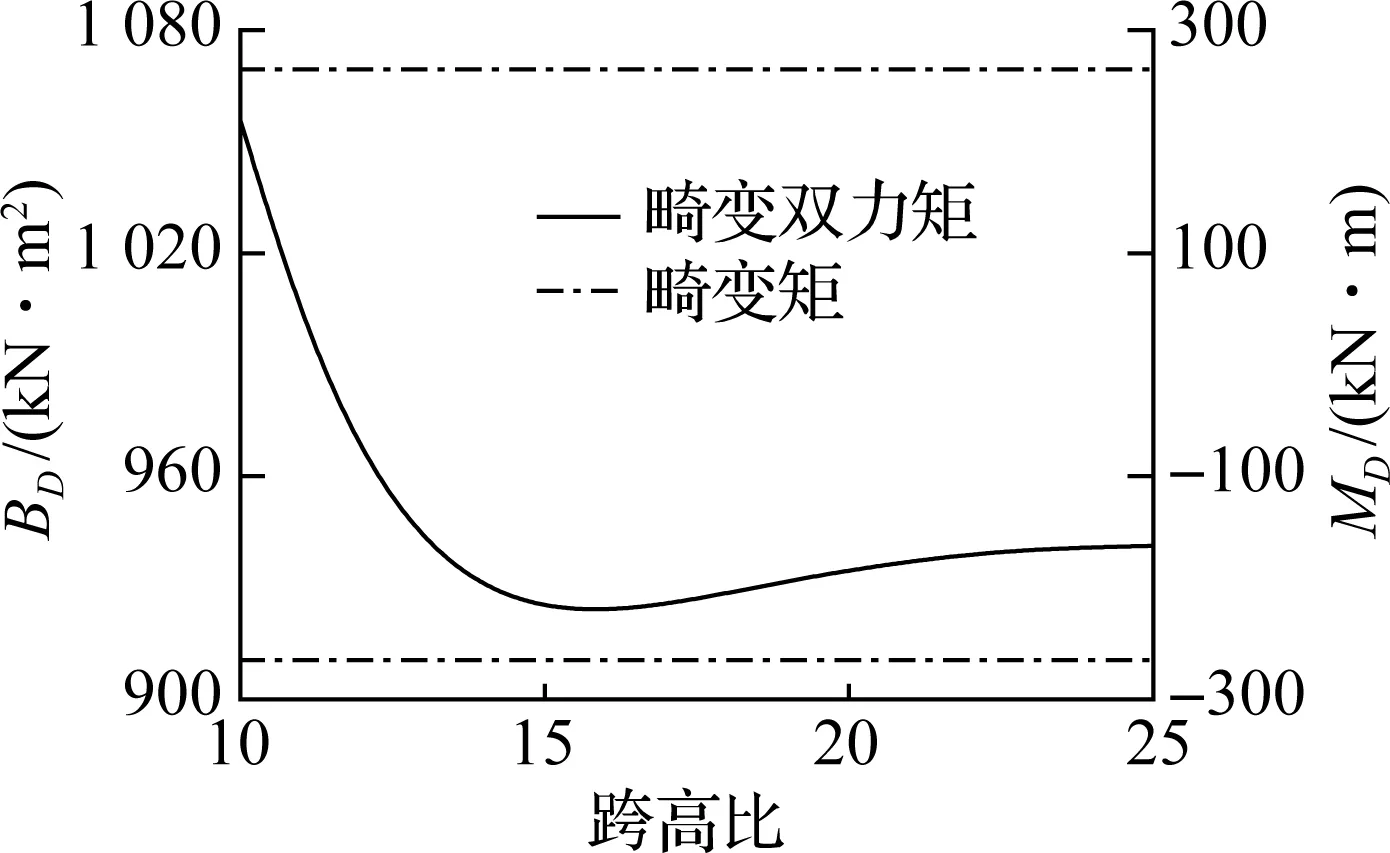
图8 箱形梁畸变内力
图9为本例箱形梁畸变内力随几何特性λ的变化曲线图.由图可知,随着λ的逐渐增大,箱形梁畸变内力逐渐减小.当λ<0.08时,畸变内力降低幅度较大;当λ>0.08时,其降低幅度较小.由图9(a)可知,当λ较小时,双力矩在梁跨结构上呈线性分布,表现出与初等梁弯矩类似的分布规律,而当λ逐渐增大时,畸变双力矩在荷载作用处较大,而在远离荷载作用处时以较快的速度衰减.图9(b)展示了畸变矩的变化规律.从图中可以看出,跨中截面畸变矩不随λ的变化而变化,即跨中截面畸变矩与箱形梁横截面尺寸无关.当λ较小时,畸变矩在梁跨结构上均匀分布,表现出与初等梁剪力类似的分布规律.当λ逐渐增大时,畸变矩同样在远离荷载作用处时以较快的速度衰减.

(a) 畸变双力矩
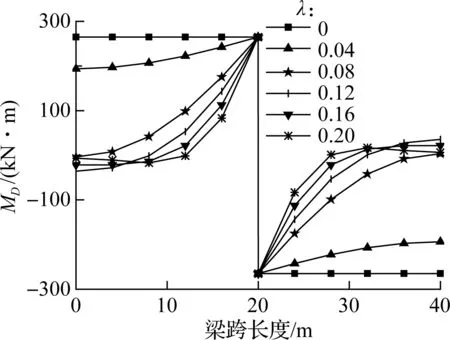
(b) 畸变矩
图10为几何特性参数λ随横截面梁高的变化曲线.由图可知,λ随着梁高的增大而逐渐减小,而畸变内力、畸变应力与λ成负相关,即随梁高的增大而增大.
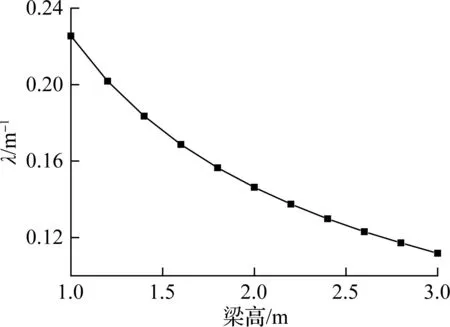
图10 λ随梁高的变化规律
图11为几何特性参数λ随箱壁厚度的变化曲线.由图可知,λ随着箱壁厚度基本呈线性增大,即畸变内力和畸变应力随着箱壁厚度的增大而逐渐减小.这进一步说明λ可以很好地反映箱形梁的畸变效应.
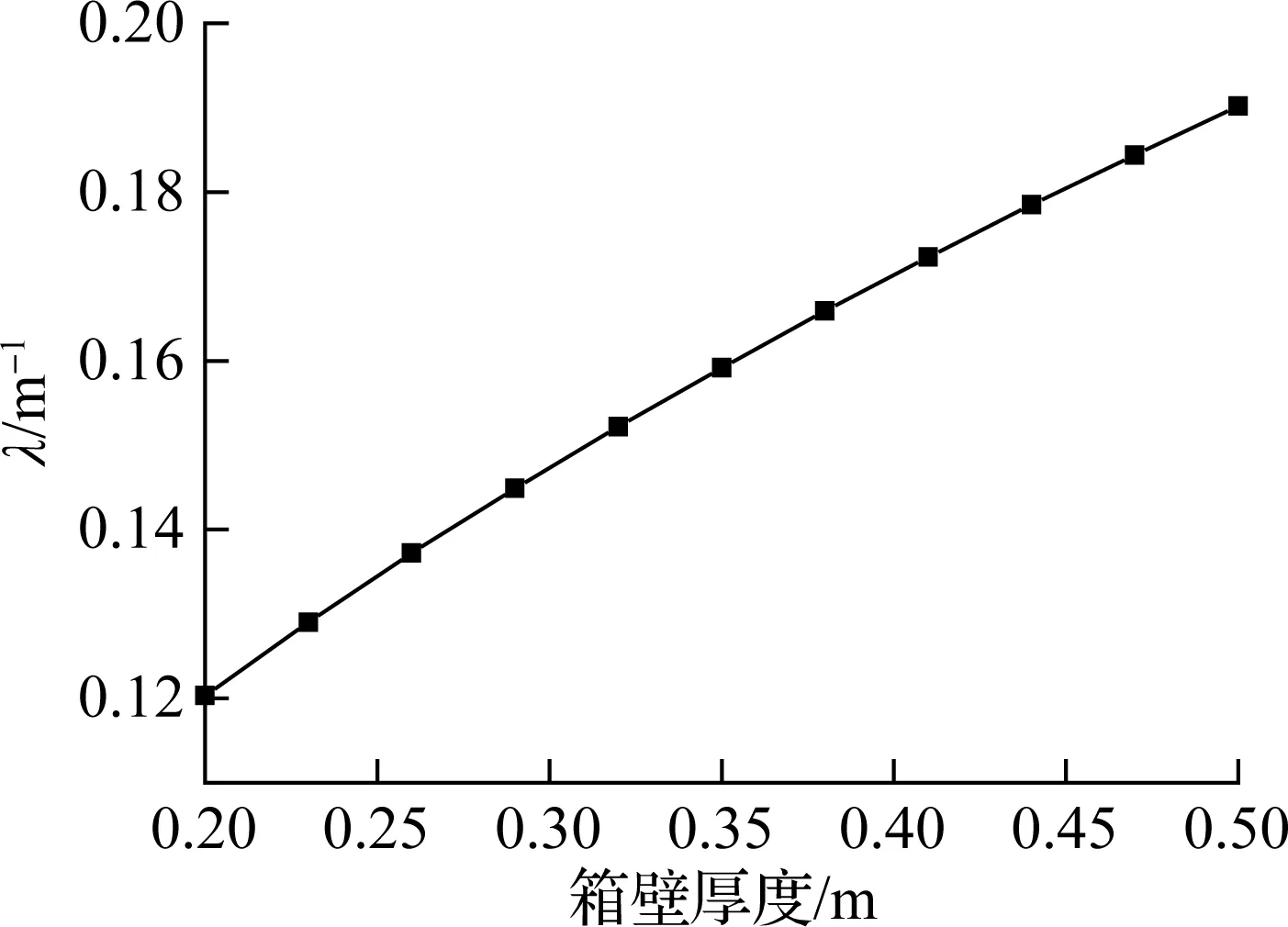
图11 λ随箱壁厚度的变化规律
5 结论
1) 应用基于最小势能原理的能量变分法,建立了单箱单室箱形梁的畸变控制微分方程,并推导求得了畸变内力.数值算例表明,本文解析法求得的畸变翘曲应力与ANSYS有限元仿真模拟所得的结果吻合良好,充分验证了本文方法的合理性.
2) 随着箱形梁跨高比的增加,箱形梁跨中横截面上的畸变矩保持不变,而跨中横截面上的畸变双力矩呈现出先减小后增大的趋势.
3) 箱形梁横截面畸变几何特性参数λ综合反映了箱形梁横截面尺寸对箱形梁畸变效应的影响.当λ较小时,畸变双力矩表现出与初等梁弯矩类似的分布规律,畸变矩表现出与初等梁剪力类似的分布规律.随着λ逐渐增大,畸变内力在远离荷载作用处以较快的速度衰减.
4) 畸变内力、畸变应力与几何特性参数λ成负相关,畸变几何特性参数λ随着梁高的增大而逐渐减小,即畸变内力和畸变应力随梁高的增大而逐渐增大.几何特性参数λ随着箱壁厚度基本呈线性增大,即畸变内力和畸变应力随着箱壁厚度的增大而逐渐减小.
