构建“学为中心悟在其中”的数学课堂——以《用平移的方法解决不规则图形面积问题》一课教学为例

陈元隆

在聚焦核心素养的当下，当课程意识由知识意识——能力意识——素养意识转变的时候，我们的数学课堂必须与时俱进，进行一些改进。史宁中教授在谈数学教学时指出，学生是否会想问题不是老师教会的，是自己领悟出来的，是一种经验的积累，所以老师要帮助学生积累经验，一个是思维的经验：会想问题；一个是做事的经验：会做事情，这两个经验是很重要的。最后加上一句话，形成数学的核心素养。可见，在学习的过程中，有效引导学习主体进行做中悟、思中悟，才是促进学生核心素养的有效策略。基于此，我觉得核心素养下的数学课堂不仅要关注教与学的方式，更要关注学习者主体“悟”的状况。下面以《用平移的方法解决不规则图形面积问题》一课为例，谈谈自己落实“学为中心、悟在其中”理念的实践与思考。

一、精选学习材料，让学生在自主体验中“悟之有物”

赞可夫认为：教会学生感悟，是一生中最有价值的本钱。数学教学过程就是学生在教师的引导下，领悟、探索数学问题解决方法的过程。课堂上动手操作、自主体验是学生悟的“源泉”。如果“做（操作）”是动手、动眼的外在活动，则“悟（领悟）”是动脑、动心的内在活动。只有当“操作”和“悟”有机融合起来，学习才真正发生。基于此，我在设计本节课时，精心选择学习材料，力求让学生在自主体验中“悟之有物”。

1.“选之有道”从有到优。

在研究《用平移的方法解决不规则图形面积问题》一课时，“如何让学生深入体验，感受平移在图形转化过程中的作用”是我一直在琢磨和思考的。在教学实践中我也尝试着不断优化学生的研究材料，我把几种课堂上学生实践操作的材料进行了对比。（见下表）

材料3材料2材料1

综上可见，聚焦核心素养，从提升学生“三会”的目标来看，材料2更有利于学生观察、思考和表达，让学生做中有悟。

2.“用之有方”从单一到多元。

在自主体验的环节，基于学生的个体差异，我还提供了一组材料包，供学生自主选择使用。此外为了让每一个学生进入研究的状态，我还设计了一份《研究单》。

（1）提供材料包——满足学生多样化学习的需求。

（2）提供《研究单》——让学习有方可循。

实践表明：当教师提供给学生的材料尽可能多样时，学生的相异构想才会充分表征出来。在自主探究的过程中，《研究单》成了学生隐形的老师，让学生的自主探究更有序、更深入，这也为学生悟数学打下了基础。

二、创设互学互研的学习场，让学生在对比表征中“悟之有序”

如果说动手实践、自主体验让学生的悟有了根基，那么在课堂教学中，有效引导学生对彼此的相异构想进行观察、比较、表达，引导学生在对比中观察、对比中思考、对比中阐述则是悟的关键。为此，我在这节课的“反馈交流”环节，试图带领学生走入悟的三个境界。

1.用数学的眼光来观察，异中求同，“悟”其中之法。

经过学生自主探究后，在反馈交流环节，作为教师，我试图把学生的相异构想充分展示出来，让学生在观察、比较中感悟解题策略的多样性。

如，在交流反馈中，我有意识把学生的不同的解题策略进行呈现，在分享过程中，充分引导学生用数学的眼光来观察，用数学的思维来分析，用数学的语言来表达，提升学生数学素养。

方法1：主要运用数方格的策略，在具体数的过程中，把不满一格的，通过图形凑整的方式，算出一共有几格。

方法2：运用平移的方法将不规则图形转化成一个规则的图形。

表面看，这两种方法不同，但深入比较我们会发现，这两种方法异中有同——数方格中的不满格图形凑整过程，不规则图形割补、平移的过程，实质都是图形转化中的“等积变形”。

2.用数学的方式来表达，同中求异，“悟”其中之能。

在指向核心素养的数学课堂中，我们不能仅仅满足学生“听懂了”这个层面，许多时候我们需要引导学生“听明白——说明白——写明白”。在《用平移的方法解决不规则图形面积问题》的学习过程中，许多学生都想到了“平移”的策略，但是学生把他们的想法记录在《研究单》时，呈现出来的却又“各不相同”。教学中要注意有效运用学生动态生成的“学习资源”，让学生在观察中比较，比较中互相学习，比较中感悟。

课堂上我有意呈现了同一策略下不同学生的《研究单》，并让学生边观察边思考：你最喜欢哪幅作品？为什么？

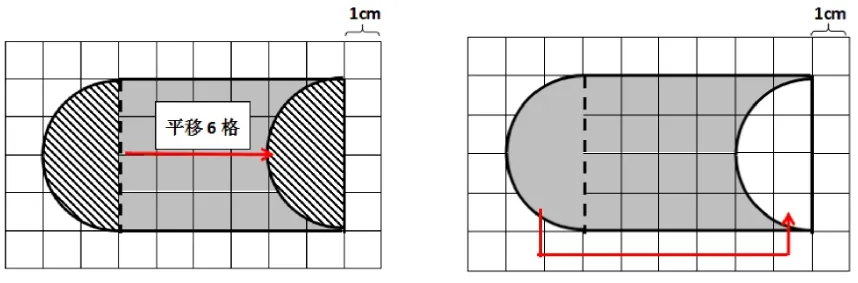
作品1呈现要素：有数据标注、有箭头提示、有阴影。

作品2呈现要素：有虚线标注。

作品3呈现要素：有数据标注、有箭头、有阴影、有文字描述。

作品4呈现要素：有虚线提示、有箭头标注。

在比较中，学生自然而然感悟到，在记录自己的思考过程时，不仅仅可以用文字，有时用一些简单的符号、记号可以把动态的操作过程用直观的方式表征出来。如用虚线可以简洁地表示分割；用阴影可以表示补上去的部分；用箭头可以表示图形运动的轨迹；图形运动的距离可以用数据标注……

可以说这些数学表征的技能，并不是由教师直接教给学生，而是让学生在学习同伴作品中、在观察比较中感悟到数学表征的多样性和简洁性。

3.用数学的思维来思考，变中求联，“悟”其中之道。

数学是思维的体操，让学生进入思维的世界，领悟数学的本质，才是数学学习之道。在《用平移的方法解决不规则图形面积问题》的教学中，基于对数学转化思想的深度理解和对“平移”的特点和性质的理解，引导学生对不同的平移方法进行了对比思考。

师：在解决这个不规则图形的面积问题时，我们可以运用平移的方法来解决，比较这些平移的方法，它们有什么不同，又有什么相同的地方？

生1：（相同点）都是通过平移，把不规则图形转化成了规则的图形。

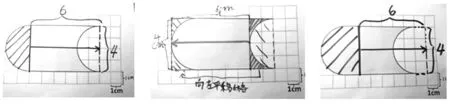
生2：（相同点）都运用了平移的方法，平移的距离都是6格。

生3：（不同点）平移的方向可以不同。

生4：（不同点）图形分割位置可以不同。我们可以沿着图形的任何一条竖线剪开，进行平移转化成长方形。

通过多元表征———观察比较——思考质疑，学生从变中求联，发现平移过程中的本质特点。

三、留给学生充分的思考时间，让学生在构建认知体系中“悟之有道”

数学家迪厄多内认为：解决一个数学问题，首先不是逻辑，而是对这个问题的感悟。这只有在问题解决的过程中，以自主体验的形式逐步生成，通过主体实践活动的直接体验，获得感性认识，并在“悟”数学的过程中建构并完善原有的认知体系。基于此，我在这节课的设计中采用大板块推进、大问题引领的方式建构教学流程。

1.大板块推进，留给学生悟的时间和空间。

本节课，我以“学为中心”为主旨，采用“自主体验——对比表征——认知建构”推进课堂学习，每一环节力求充分调动学生学习的积极性，让学生成为学习的主人，教师成为引领者、组织者和合作者，引导学生悟“平移”，悟“转化”之道，弱化教的痕迹，放大学生的学和悟，让学生在悟中学。

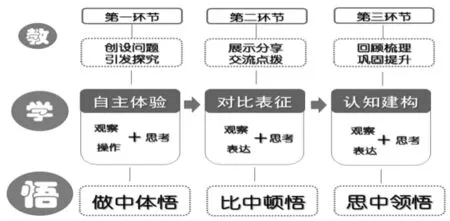
2.大问题引领，让学生领悟数学思想。

从数学思想的特点和形成过程来说，对学生数学思想的渗透不是立竿见影的，而是需要有一个不断渗透、循序渐进、由浅入深的过程。教师必须基于学生的“研究情况”适时地进行启发、点拨，让学生的思维水平更上一层楼。

当大多数学生能精准描述如何运用平移的策略将不规则图形转化成规则图形，推导出不规则图形面积的时候，我紧跟着追问学生：为什么要将这个不规则图形变一变，转化成长方形？这个问题促使学生对数学学习的本质思考——在学习的过程中我们会遇到许多新问题、新情况，有些时候，我们可以把未知的问题通过一定的方法转化成已知问题，用已有的知识、技能、策略解决新问题。

实践表明：有效追问、及时小结都是促进学生深度思考的有效策略。

学习过程中，只有当学习者主体对学习内容有所感悟的时候，学习才真正开始。当课程意识由知识意识——能力意识——素养意识的时候，我们的数学课堂必须与时俱进，构建“学为中心，悟在其中”的课堂，让学生乐于“悟”、勤于“悟”。