初中数学例习题的教学策略研究
2019-01-03赵正萍
赵正萍

[摘 要] 例习题教学不仅为学生提供了解决问题的范例,规范了思考的过程,还为数学方法体系的建构提供了基础,引领了学生的思维. 在教学中需要教师理解并把握教材重点,精心编制例习题,巧借变式训练,运用分层训练,进一步发展学生的思维能力,实现共同进步.
[关键词] 初中数学;例习题教学;一题多解;一题多变
例习题教学在新知识的讲解过程和巩固练习中都发挥着举足轻重的作用,它可以有效增强学生解决问题的能力,可以培养学生的思维水平,可以提升数学教学的智力,还可以促进良好数学观念的日益成熟. 为此,教师在教学中须遵循新课标导向,精心编制例习题,加以变式训练,运用分层训练,拓宽学生的学习领域,发展学生的思维,让学生获取成功的体验,增强学好数学的信心.
精选例习题,力求准确到位
在教学过程中,教师需基于教学目的,创造性地使用教材并遵循学生的认知过程. 所精选的例习题,需具有典型性和代表性,同时需兼顾知识点的涉及面,有机结合基础型和发展型训练,让有限的例题发挥出巨大的作用,引导学生完善解题路径,促进学生条理化、系统化地掌握知识,提高解题能力,优化思维品质.
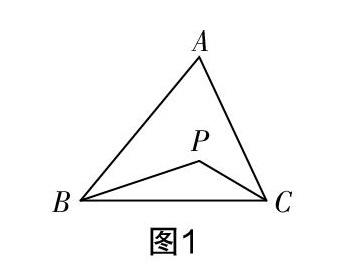
例1如图1所示,若判断以下△ABC的面积为△PBC的几倍,提供一把有刻度的直尺,最少需度量的次数是______.
[图1]
分析 此例题是对学生基础知识进行考查的一种题型. 而它又不同于一般的基础题,是创新式题型,引领学生借助已学基础知识去理解数学本质,并合理有效地解决问题. 教师可引导学生从实践操作入手,要求学生度量点A和点P到BC的距离,并至少进行两次重复实验. 通过开放式的解题过程,一方面满足了学生活泼好动的心理需求,另一方面也为学生的自主探究和感悟数学本质创造了契机. 学生通过思考、操作、交流等操作过程,获取完善的数学认知,活跃了思维,拓宽了视角.
巧借变式训练,促进学生思考
在教学中,教师可以将教材中的例习题当作变式的主体,而后由这个主体进行变换和延展,由浅入深、由易到难、层层递进,通过逐步深入的引导,增强学生的数学逻辑推理能力,有效锻炼学生的思维.
1. 以“问题链”为指引
问题是引领学生思考的重心,是培养思维能力的最佳途径. 在例习题教学中,教师可以借助一系列“问题链”引领学生的思维,帮助学生由低阶思维向高阶思维逐步过渡,从简单的记忆、理解和应用慢慢过渡至分析、反思和评价,从而多方位、多角度地训练学生的思维能力和智力,培养学生的探究精神和创新能力.
例2以“一元二次方程根与系数的关系”的教学片段为例.
问题1:请求出以下一元二次方程x2+6x+9=0,x2+5x+6=0的两根、两个根的和以及两个根的积,同时仔细观察以上方程中根和系数之间存在什么关系?
问题2:请求出以下一元二次方程2x2-5x-3=0,3x2-10x+8=0的两根、两个根的和以及两个根的积,同时仔细观察以上方程中根和系数之间存在什么关系?
问题3:如果x,x是一元二次方程ax2+bx+c=0(a≠0)的两个根,猜猜两个根的和、两个根的积各为多少?这里的方程中根与系数又存在什么关系呢?
问题4:以上罗列出的规律是否适用于所有的一元二次方程?方程x2+x+1=0的根也符合以上规律吗?
问题5:思考并利用数学语言阐述以上规律.
分析 教师利用“问题链”步步深入,贯穿于解决问题的始终,巧妙地把握学生的思维,有效地实现了知识点之间的串联,促进学生灵活运用知识和解决问题,逐步提升学生自主探究的动力和意识,促进学生积极参与、主动思考、乐于探索,有效地迁移运用知识,以实现学习目标的高效达成.
2. 一题多解
通过一题多解,可以有效激活学生思维的发散性. 学生可以从多个角度和多个途径去找寻解决问题的方法和策略,从不同角度、不同方位去思考问题,使学生的思维多方向延展,能增强学生思维的创造性和发散性.
例3已知x-1=,请求出(x+1)2-4(x+1)+4的值为多少?
解法1:因为 x-1=,所以x=+1,所以原式=
+1+12-4
+1+1+4=3.
解法2:因为x-1=,x+1=+1+1=+2,所以原式=
+22-4
+2+4=3.
解法3:原式=x2+2x+1-4x-4+4=(x-1)2=3.
解法4:原式=[(x+1)-2]2=(x-1)2=3.
分析 一題多解可以有效延伸各阶段知识之间的关联,让不同层次学生的思维都在各自的水平上有效延伸.
3. 一题多变
教材中很多概念、定理、公式都是静态的,而学生的思维是动态的、活跃的. 在例习题教学中,可以通过一题多变,如变换图形、数据、条件、结论等,保持问题的本质不变,让问题呈现梯度上升的模式,让学生全面理解知识的本质. 它有利于学生反思解决问题的过程,进而培养数学思维的深刻性.
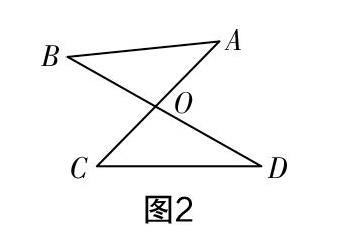
例4如图2所示,已知点O为AC,BD的交点,∠A,∠B的和是否与∠C,∠D的和相等?请证明.
变式1如图2所示,已知点O为AC,BD的交点,且∠A=∠D,那么∠B,∠C的大小关系是( ).
A. ∠B=∠C B. ∠B>∠C
C. ∠B<∠C D. 无法确定
变式2如图2所示,已知点O为AC,BD的交点,且∠A=36°,∠B=45°,∠C=48°,那么∠D=______.
